SHANNON ENTROPY AND FRACTAL ANALYSIS FOR THE 16S

RIBOSOMAL RNA AND COX2 MT-DNA SEQUENCES IN

PRIMATES INCLUDING NEANDERTHAL

N. Gadura*, Todd Holden**, G. Tremberger, Jr**, E. Cheung**

P. Schneider*, D. Lieberman** and T. Cheung**

Biology* and Physics** Departments, CUNY Queensborogh Community College, Bayside, NY 11364 U.S.A.

Keywords: Mono-nucleotide entropy, Di-nucleotide entropy, Fractal dimension, Neanderthal mt-DNA COX2,

Neanderthal mt-DNA 16S rRNA.

Abstract: The primate mt-DNA 16S rRNA and COX2 sequences, including Neanderthal sequences, were studied

using nucleotide frequency, mono- and di-nucleotide entropy, and fractal dimension. The fractal dimension

was computed with the Higuchi method when a nucleotide sequence is expressed as a numerical sequence

where each nucleotide is assigned its proton number. The results shows that the C+G percent correlates

with the fractal dimension with R-square value of around 0.88 (N = 8) for both gene sequences. The Di- and

mono-nucleotide entropy is also well correlated with similar R-square values. For the COX2 gene, the

human and Neanderthal cluster at high entropy suggests that chimp, gorilla, and orangutan were subjected to

a higher selection pressure for this gene. The human COX2 has less entropy than the Neanderthal COX2

consistent with the presence of some selection pressure.

1 INTRODUCTION

Closely related species can be classified by a

collection of phylogenetic markers with numbers

determined from mathematical operations on DNA

sequence. In cases where such markers are

significantly different from what would be expected

for random mutations, we can get an idea of how

much natural selection has influenced the evolution

of a particular gene. Here, we analyze primate mt-

DNA 16S ribosomal RNA (rRNA) and COX2

sequences, including Neanderthal sequences, using

nucleotide frequency, mono- and di-nucleotide

entropy, and fractal dimension. For protein encoded

by the mt-DNA genome, COX2 have experienced

four amino acid substitutions on the modern human

mtDNA lineage (Green et al, 2008). COX2 encodes

a protein that maintains a proton gradient across the

mitochondrial inner membrane, which drives the

phosphorylation of ADP to ATP. The conclusion

that the evolution of human COX2 from Neanderthal

has been for minor adaptive advantages without

significant functional consequences for

mitochondrial function were put forward using the

fact that the substitutions are on non-functional site

in the crystal structure. The relationship of the

above mentioned phylogenetic markers would shed

light whether there is selection pressure

corresponding to some yet to be discovered

significant function. The 16S rRNA is an important

gene in classification and is included in this study.

The nucleotide base pair changes over a gene

sequence can be viewed as a fluctuation and,

consequently, can be investigated with standard

tools that include correlation and fractal dimension

analysis. For this study, the numerical sequence

representing the fluctuation of nucleotides in a gene

sequence was generated using the proton number of

each nucleotide. This numerical series can then be

processed further using numerical methods such as a

moving average, which is often used in stock market

time series analysis. The fractal dimension of such a

random series or random series derived from the

original atomic number based sequence can be

computed. A recent comparison of human and

chimpanzee genomes revealed that it is possible to

measure the acceleration rate of the accelerated

regions of the human genome (Pollard, et al, 2006a).

The most accelerated region, HAR1, was shown by

a gene expression experiment in the human embryo

to be transcription active and co-expressed with

257

Gadura N., Holden T., Tremberger Jr G., Cheung E., Schneider P., Lieberman D. and Cheung T. (2010).

SHANNON ENTROPY AND FRACTAL ANALYSIS FOR THE 16S RIBOSOMAL RNA AND COX2 MT-DNA SEQUENCES IN PRIMATES INCLUDING

NEANDERTHAL.

In Proceedings of the First International Conference on Bioinformatics, pages 257-260

DOI: 10.5220/0002753002570260

 SciTePress

reelin, which is an essential protein involved in the

development of the six-layer cortex of the human

brain. Fractal analysis was applied to the HAR1

nucleotide sequence and the homologous sequence

in the chimpanzee genome. Analysis shows that the

differences in fractal dimension can be used as a

marker of evolution. The 118-bp in HAR1 contains

18 point substitutions over an evolutionary span of 5

million years when comparing the human to the

chimpanzee. However, the same 118-bp region only

contains two point substitutions over a span of 300

million years when comparing the chicken to the

chimpanzee. The implications of evolution and

positive selection have been discussed in recent

literature (Pollard, et al, 2006b).

2 MATERIALS & METHODS

The nucleotide sequences were downloaded from

Genbank. The accession numbers of the mtDNA

database are listed in the Appendix. The studied

primates are human, Neanderthal, chimp (chimp and

pygmy chimp), gorilla (western and western

lowland), and orangutan (Bornean and Sumatran).

The ATCG sequence was converted to a

numerical sequence by assigning the atomic number,

the number of protons, to each of the nucleotides:

A(70), T(66), C(58), G(78). The assigned number is

roughly proportional to the nucleotide mass. This

assignment was consistent with the recently reported

mass fractal analysis of a ribosome sequence (Lee

2006). The A-T and C-G pairs in a double strand

DNA would have the same value of 136.

Fractal dimension analysis can be used in the

study of correlated randomness. Among the various

fractal dimension methods, the Higuchi fractal

method is well suited for studying signal fluctuation

(Higuchi, 1998). The signal from the sequence

represents a random spatial intensity series. The

spatial intensity (Int) random series with equal

intervals could be used to generate a difference

series (Int(j)-Int(i)) for different lags in the spatial

variable. The non-normalized apparent length of the

spatial series curve is simply L(k) = Σ absolute

(Int(j)-Int(i)) for all (j-i) pairs from 1 to k. The

number of terms in a k-series varies and

normalization must be used to get the series length.

If the Int(i) is a fractal function, then the log (L(k))

versus log (1/k) should be a straight line with the

slope equal to the fractal dimension. Higuchi

incorporated a calibration division step (divide by k)

such that the maximum theoretical value is

calibrated to the topological value of 2. The detailed

calculation is given in the literature (Higuchi, 1998).

When comparing the dimension of two fractal

forms, the popular method of taking the difference

of the two Higuchi fractal dimension values is valid

to within a constant regardless of the calibration

division step. The Higuchi fractal algorithm used in

this project was calibrated with the Weierstrass

function. This function has the form W(x) = Σ a

-nh

cos (2 π a

x) for all the n values 0, 1, 2, 3… The

fractal dimension of the Weierstrass function was

given by (2 - h) where h takes on an arbitrary value

between zero and one.

The Shannon entropy of a sequence can be used

to monitor the level of functional constraints acting

on the gene (Parkhomchuk, 2006). A sequence with

relatively low nucleotide variety would have a low

Shannon entropy (more constraint) in terms of the

set of 16 possible di-nucleotide pairs. A sequence’s

entropy can be computed as the sum of (p

) log(p

)

over all states i and the probability p

can be

obtained from the empirical histogram of the 16 di-

nucleotide-pairs. The maximum entropy is 4 binary

bits per pair for 16 possibilities (2

). The maximum

entropy is 2 bits per mono-nucleotide with 4

possibilities (2

3 RESULTS & DISCUSSION

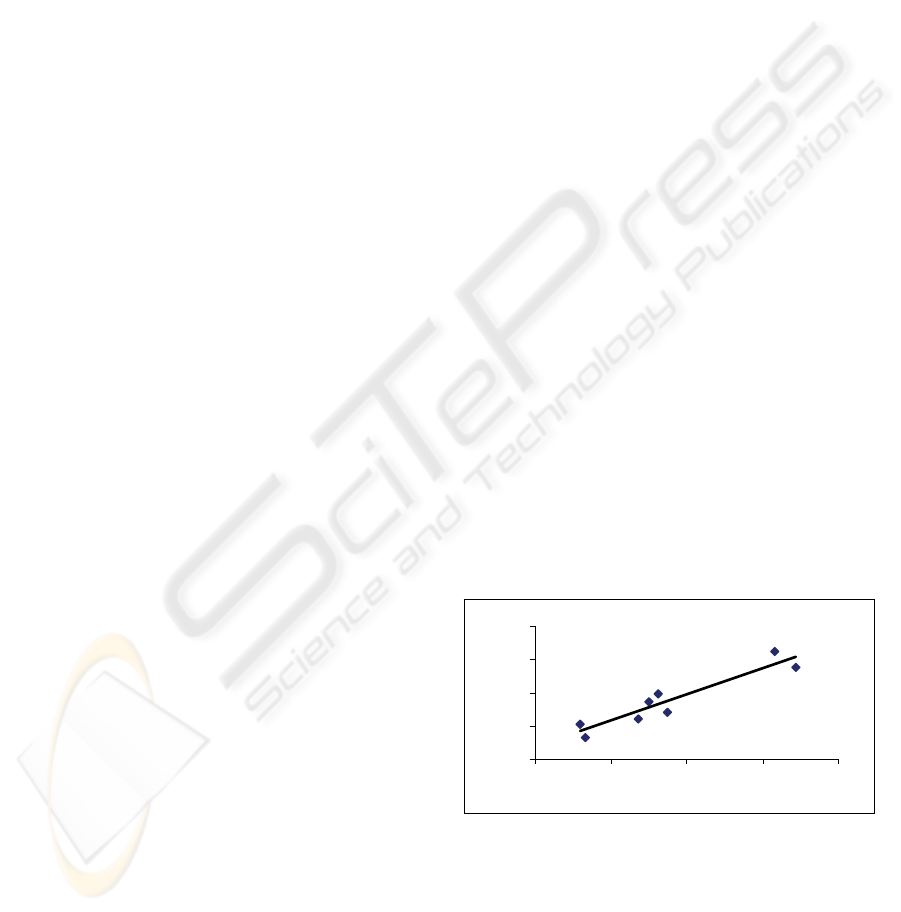
For the 16S rRNA sequences, the C+G percent

correlates with fractal dimension, FD, with R-square

value of 0.88, N = 8, in Figure 1. Dropping human

and Neanderthal data would increase the R-square

value to ~ 0.91 because the data are in the middle as

small outliers.

y = 0.7981x + 1.6265

= 0.881

1.96

1.965

1.97

1.975

1.98

0.42 0.425 0.43 0.435 0.44

Figure 1: The C+G percent (x-axis) versus FD (y-axis) for

the studied 16S rRNA sequences.

The mono-nucleotide entropy correlates with di-

nucleotide entropy in the 16S rRNA sequence with

R-square value of ~ 0.88, N = 8 (Figure 2).

Dropping human and Neanderthal increases R-

BIOINFORMATICS 2010 - International Conference on Bioinformatics

258

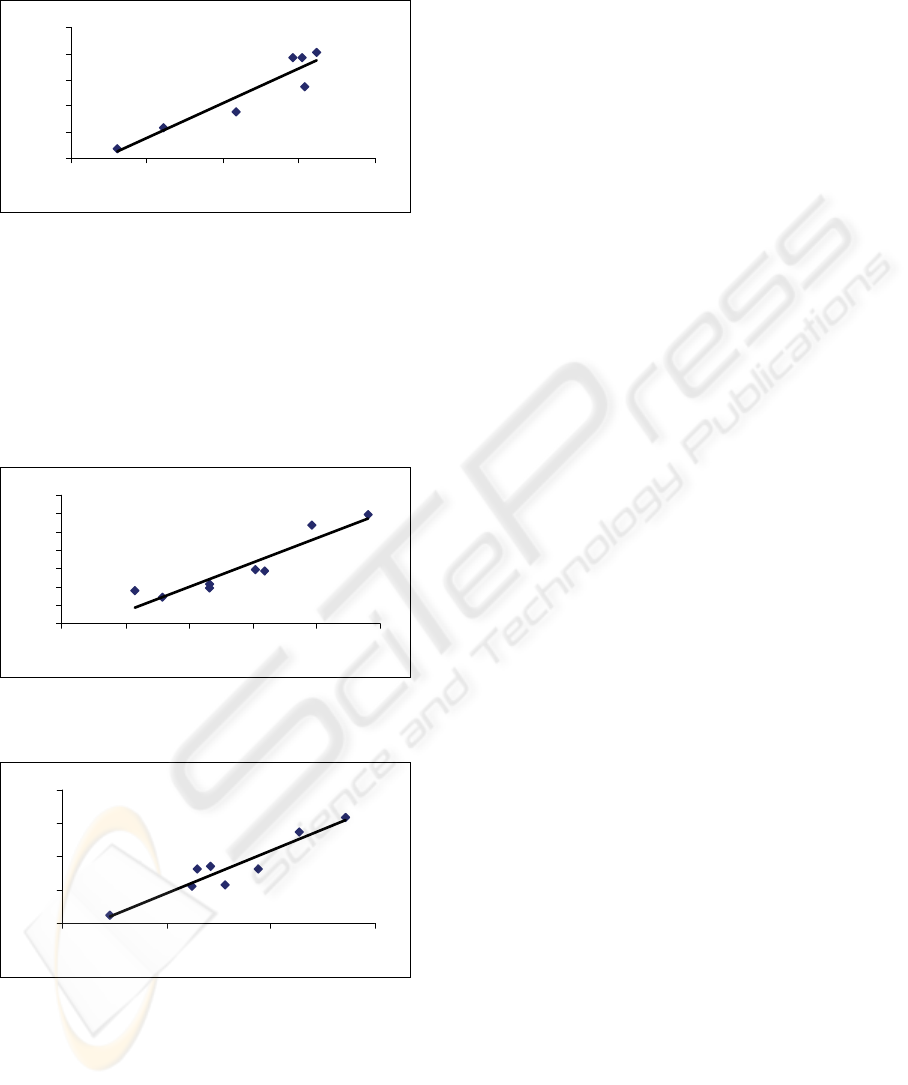
square value of ~ 0.99 because they are in the

middle as moderate outliers

y = 3.3227x - 2.5987

= 0.8838

3.87

3.875

3.88

3.885

3.89

3.895

1.946 1.948 1.95 1.952 1.954

Figure 2: The mono-nucleotide entropy (x-axis) versus the

di-nucleotide entropy (y-axis) for the studied 16S rRNA

sequences.

Similar correlation of the C+G percent with FD is

observed for COX2 sequences R-square value of ~

0.8756, N = 8 (Figure 3). Dropping the human and

Neanderthal data would increase the R-square value

to ~ 0.93 because they are in the middle as moderate

outliers.

y = 1.3163x + 1.3876

= 0.8756

1.96

1.97

1.98

1.99

2.01

2.02

2.03

0.43 0.44 0.45 0.46 0.47 0.48

Figure 3: The C+G percent (x-axis) versus FD (y-axis) for

the studied COX2 sequences.

y = 2.5412x - 1.0639

= 0.8979

3.87

3.88

3.89

3.9

3.91

1.94 1.945 1.95 1.955

Figure 4: The mono-nucleotide entropy (x-axis) versus the

di-nucleotide entropy (y-axis) for the studied COX2

sequences.

Similar correlation of the single entropy with pair

entropy is observed for COX2 sequences R-sq ~

0.8979 (Figure 4). The interesting point is that if

human and Neanderthal are deleted then the

correlation drops to 0.7601 because they are the two

end points at large values (mono-nucleotide entropy

for Neanderthal ~ 1.953 bits, for human 1.951 bits).

Correlation would suggest similar selection

pressure mechanism. Conserved regions would

imply less random nucleotide fluctuation across

species and the fractal dimension would differ from

2 and the di-nucleotide Shannon entropy would be

smaller than 4 bits. Our previous results have

associated fractal dimension with functionality

(Tremberger, Jr., et al., 2009). The observation of

fractal dimension correlation to the C+G percent

(which is correlates to the A+T percent) shows that

human and Neanderthal occupy the mid range region

and thus would indicate a mild selection pressure on

the functionality of the 16S ribosomal RNA and

COX2 sequences as compared to the other primates.

Our previous results have associated entropy with

constrains (Holden et al, 2008). The high-value

positions of the COX2 sequences in the single-

entropy and pair entropy correlation suggests a

weaker constraint in human and Neanderthal as

compared to other primates. Di-nucleotide

frequency distributions confirm the closeness of

relations among the various primates. For the COX2

genes, lowered entropy is largely a manifestation of

high Cytosine (~30 %) and low Guanine (~15 %)

content. Di- and mono-nucleotide entropy is well

correlated. That human and Neanderthal cluster at

high entropy indicates that chimp, gorilla, and

orangutan were subjected to a higher selection

pressure for this gene. The human COX2 has less

entropy than the Neanderthal COX2 consistent with

the presence of some selection pressure.

Whether the mild selection pressure and the

weak constraint observed in the mtDNA 16S rRNA

and COX2 sequences have activated other selection

response such as those observed in the brain

function related HAR1 sequence is an interesting

consideration. The HAR1 hardly evolved in 300

million years from chicken to chimp and then

experienced accelerated selection pressure. The

fractal analysis shows that the HAR1 has a fractal of

2.02 while the chimp is at 1.97, the di-nucleotide

entropy is 3.86 bits for human and 3.64 bits for

chimp; and single entropy is 1.97bits for human,

1.86 bits for chimp. If the HAR1-like activation

exists such that the selection pressure would be mild

on the mt-DNA, it would suggests that the

Neanderthal would have similar HAR1-like response

as their 16S rRNA and COX2 sequences are very

similar to the human’s in terms of the above studied

parameters. The activation would be an indication

of cooperation in multi-cellular organism. In this

regard the CNV (copy number variants) strategy

SHANNON ENTROPY AND FRACTAL ANALYSIS FOR THE 16S RIBOSOMAL RNA AND COX2 MT-DNA

SEQUENCES IN PRIMATES INCLUDING NEANDERTHAL

259

should also be considered. It is possible that less

demand on the Cs and Gs with multiple copies could

be more advantageous than higher demand on Cs

and Gs bias with fewer copies for responding to

selection pressure. The correlation analysis method

can be a good supplemental tool to the relative

comparison method inherent in the BLAST method.

4 CONCLUSIONS

The nucleotide fluctuation of the mtDNA 16S rRNA

and COX2 gene sequences in primates including

Neanderthal were studied. The tools are fractal

dimension, Shannon mono- and di-nucleotide

entropy, and C+ G content. We found that C+G

content correlates with the fractal dimension. The

correlation of the mono- and di-nucleotide entropy

shows that the human COX2 gene has experienced

some selection pressure. Future studies include the

extension to other species.

ACKNOWLEDGEMENTS

The project was partially supported by several

CUNY PSC and Collaborative grants. N.G.

received partial support from CUNY Collaborative

CCIRG and Perkins Grant. E.C. thanks the

hospitality of QCC. We thank the research groups

for posting their gene sequence data in Genbank.

REFERENCES

Green, RE, 2008, Malaspinas AS, et al. “A Complete

Neandertal Mitochondrial Genome Sequence

Determined by High-Throughput Sequencing”, Cell,

134, 416-426.

Holden, T. 2008, G. Tremberger, Jr., P. Marchese, E.

Cheung, R. Subramaniam, R. Sullivan, P. Schneider,

A. Flamholz, D. Lieberman, & T. Cheung, “DNA

sequance based comparative studies of between non-

extremophile and extremophile organisms with

implications in exobiology”, SPIE Proceedings,

70970Q, (12 pages) invited.

Higuchi, T., 1998, "Approach to an irregular time series

on the basis of fractal theory", Physica D vol 31, 277-

283.

Lee, Chang-Yong, 2006 “Mass Fractal Dimension of the

Ribosome and Implication of its Dynamic

Characteristics”, Physical Review E 73, 042901.

Parkhomchuk, DV, 2006 ” Di-nucleotide Entropy as a

Measure of Genomic Sequence Functionality”,

arXiv:q-bio/0611059

Pollard, KS 2006a, Salama SR, Lambert N, Coppens S,

Pedersen JS, et al., “An RNA gene expressed during

cortical development evolved rapidly in humans”.

Nature 443, 167-172.

Pollard KS, 2006b, Salama SR, King B, Kern AD, Dreszer

T, et al. “Forces shaping the fastest evolving regions

in the human genome”, PLoS Genet 2(10): e168. DOI:

10. 1371/journal.pgen.0020168

Tremberger, Jr., George, E. Cheung; N. Gadura; T.

Holden; R. Subramaniam; R. Sullivan; P. Schneider;

A. Flamholz; D. Lieberman; T. Cheung, “Multi-fractal

property of perchlorate reductase gene sequences and

DNA photonics application to UV fluorescence

detection on Mars-like surface”, SPIE Proceedings

Vol. 7441, 74410G, (10 pages) invited, 2009

APPENDIX

The studied sequences were downloaded from the

Genbank mtDNA database. The accession numbers

are:

NC_001644 Pan paniscus mitochondrion, (pygmy

chimpanzee).

NC_001643 Pan troglodytes mitochondrion,

(chimpanzee).

NC_011120 Gorilla gorilla gorilla mitochondrion

(Western lowland gorilla).

NC_001645 Gorilla gorilla mitochondrion (Western

Gorilla).

AC_000021 Homo sapiens mitochondrion, (human).

NC_011137 Homo sapiens neanderthalensis

mitochondrion, (Neanderthal).

NC_001646 Pongo pygmaeus mitochondrion

(Bornean orang-utan).

NC_002083 Pongo abelii mitochondrion, (Sumatran

orangutan).

BIOINFORMATICS 2010 - International Conference on Bioinformatics

260