
IMPROVED MULTISTAGE LEARNING
FOR MULTIBODY MOTION SEGMENTATION
Yasuyuki Sugaya
Department of Computer Science and Engineering, Toyohashi University of Technology, Toyohashi, Aichi 441-8580, Japan
Kenichi Kanatani
Department of Computer Science, Okayama University, Okayama 700-8530, Japan
Keywords:
Multibody motion segmentation, GCAP, Taubin method, EM algorithm, Multistage optimization.
Abstract:
We present an improved version of the MSL method of Sugaya and Kanatani for multibody motion segmen-
tation. We replace their initial segmentation based on heuristic clustering by an analytical computation based
on GPCA, fitting two 2-D affine spaces in 3-D by the Taubin method. This initial segmentation alone can
segment most of the motions in natural scenes fairly correctly, and the result is successively optimized by the
EM algorithm in 3-D, 5-D, and 7-D. Using simulated and real videos, we demonstrate that our method out-
performs the previous MSL and other existing methods. We also illustrate its mechanism by our visualization
technique.
1 INTRODUCTION
Separating independently moving objects in a video
stream has attracted attention of many researchers in
the last decade, and today we are witnessing a new
surge of interest in this problem. The most classical
work is by Costeira and Kanade (1998), who showed
that, under affine camera modeling, trajectories of im-
age points in the same motion belong to a common
subspace of a high-dimensional space. They seg-
mented trajectories into different subspaces by zero-
nonzero thresholding of the elements of the “interac-
tion matrix” computed in relation to the “factorization
method” for affine structure from motion (Poelman
and Kanade, 1997; Tomasi and Kanade, 1992). Since
then, various modifications and extensions have been
proposed. Gear (1998) used the reduced row eche-
lon form and graph matching. Ichimura (1999) used
the Otsu discrimination criterion. He also used the
QR decomposition (Ichimura, 2000). Inoue and Ura-
hama (2001) introduced fuzzy clustering. Kanatani
(2001, 2002, 2002a) combined the geometric AIC
(kaike Information Criterion) (Kanatani, 1996) and
robust clustering. Wu et al. (2001) introduced orthog-
onal subspace decomposition. Sugaya and Kanatani
(2004) proposed a multistage learning strategy using
multiple models. Vidal et al. (2005, 2008) applied
their GPCA (Generalized Principal Component Anal-
ysis), which fits a high-degree polynomial to multiple
subspaces. Fan et al. (2006) and Yan and Pollefeys
(2006) introduced new voting schemes for classifying
points into different subspaces in high dimensions.
Schindler et al. (2008) and Rao et al. (2008) incorpo-
rated model selection based on the MDL (Minimum
Description Length) principle.
At present, it is difficult to say which is the best
among all these methods. Their performance has been
tested, using real videos, but the result depends on the
test videos and the type of the motion that is taking
place (planar, translational, rotational, etc.). If such
distinctions are disregarded and simply the gross cor-
rect classification ratio is measured using a particular
database, typically the Hopkins155 (Tron and Vial,
2007), all the methods exhibit more or less similar
performance.
A common view behind existing methods seems
to be that the problem is intricate because the seg-
mentation takes place in a high-dimensional space,
which is difficult to visualize. This way of thinking
has lead to introducing sophisticated mathematics one
after another and simply testing the performance us-
ing the Hopkins155 database. In this paper, we show
that the problem is not difficult at all and that the ba-
sis of segmentation lies in low dimensions. Indeed,
199
Sugaya Y. and Kanatani K. (2010).
IMPROVED MULTISTAGE LEARNING FOR MULTIBODY MOTION SEGMENTATION.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 199-206
DOI: 10.5220/0002814601990206
Copyright
c
SciTePress

we can visualize what is going on in 3-D. This re-
veals that what is crucial is the type of motion and
that different motions can be easily segmented if the
motion type is known.
Sugaya and Kanatani (2004) assumed multiple
candidate motion types and presented the MSL (Mul-
tiStage Learning) strategy, which does not require
identification of the motion type. To do this, they
exploited the hierarchy of motions (e.g., translations
are included in affine motions) and applied the EM
algorithm by progressively assuming motion models
from particular to general: Once one tested motion
type agrees with the true one, the segmentation is un-
changed in the subsequent stages because general mo-
tions include particular ones. Tron and Vidal (2007)
did extensive comparative experiments and reported
that MSL is highly effective. In this paper, we present
an improved version of MSL.
Since MSL uses the EM algorithm, we need to
provide an appropriate initial segmentation, which is
the key to the performance of the subsequent stages,
in which the segmentation in the preceding stage is
input and the output is sent to the next stage. For com-
puting the initial segmentation, MSL used a rather
heuristic clustering that combines the interaction ma-
trix of Costeira and Kanade (1998) and model selec-
tion using the geometric AIC (Kanatani, 1996). In
this paper, we replace this by the GPCA of Vidal et
al. (2005, 2008): we fit a degenerate quadric in 3-D
by the method of Taubin (1991). Then, we succes-
sively apply the EM algorithm and demonstrate, us-
ing the Hopkins155 database, that our method out-
performs MSL and other existing methods. We also
show, using our visualization technique, why and how
good segmentation results.
2 AFFINE CAMERAS
Suppose N feature points {p
α
}are tracked overM im-
age frames. Let (x
κα
,y
κα
), κ = 1, ..., M, be the image
coordinates of the αth point p
α
in the κth frame. We
call the 2M-D vector
p
α
= (x
1α
, y
1α
, x
2α
, y
2α
, ··· x
Mα
, y
Mα
)
⊤
, (1)
the trajectory of p
α
. Thus, an image motion of each
point is identified with a point in 2M-D. We define
a camera-based XYZ coordinate system such that the
Z-axis coincides with the camera optical axis and re-
gard the scene as moving relative to a stationary cam-
era. We also define a coordinate system fixed to each
of the moving objects. Let (a
α
,b
α
,c
α
) be the coordi-
nates of point p
α
with respect to the coordinate sys-
tem of the object it belongs to. Let t
κ
be the origin of
that coordinate system and {i
κ
,j
κ
,k
κ
} the basis vec-
tors in the κth frame. Then, the 3-D position r
κα
of
the point p
α
in the κth frame with respect to the cam-
era coordinate system is
r
κα
= t
κ
+ a
α
i
κ
+ b
α
j
κ
+ c
α
k
κ
. (2)
The affine camera, which generalizes ortho-
graphic, weak perspective, and paraperspective pro-
jections (Poelman and Kanade, 1997), models the
camera imaging by
x
κα
y
κα
= A
κ
r
κα
+ b
κ
, (3)
where the 2 ×2 matrix A
κ
and the 2-D vector b
κ
are
determined by the intrinsic and extrinsic camera pa-
rameters of the κth frame. By substitution of Eq. (2),
Eq. (3) is written in the form
x
κα
y
κα
=
˜
m
0κ
+ a
α
˜
m
1κ
+ b
α
˜
m
2κ
+ c
α
˜
m
3κ
, (4)
where
˜
m
0κ
,
˜
m
1κ
,
˜
m
2κ
, and
˜
m
3κ
are 2-D vectors de-
termined by the intrinsic and extrinsic camera param-
eters of the κth frame. The trajectory in Eq. (1) is
expressed as the vertical concatenation of Eq. (4) for
κ = 1, ..., M, in the form
p
α
= m
0
+ a
α
m
1
+ b
α
m
2
+ c
α
m
3
, (5)
where m
i
, i = 0, 1, 2, 3, are the 2M-D vectors consist-
ing of
˜
m
iκ
for κ = 1, ..., M.
3 GEOMETRIC CONSTRAINTS
Equation (5) states that the trajectories of points that
belong to the same object are in a common “4-D
subspace” spanned by {m
0
, m
1
, m
2
, m
3
}. Hence,
segmenting trajectories into different motions can be
done by classifying them into different 4-D subspaces
in 2M-D. However, the coefficient of m
0
in Eq. (5)
is identically 1, which means that the trajectories of
points that belong to the same object are in a common
“3-D affine space” passing through m
0
and spanned
by {m
1
, m
2
, m
3
}. Thus, segmentation can also
be done by classifying trajectories into different 3-D
affine spaces in 2M-D.
In real situations, however, objects and a back-
ground often translate with rotations only around an
axis vertical to the image plane. We say such a mo-
tion is planar; translations in the depth direction can
take place, but they are invisible under the affine cam-
era modeling, so we can regard translations as con-
strained to be in the XY plane. It follows that if we
take the basis vector k
κ
in Eq. (2) to be in the Z di-
rection, it is invisible to the camera, and hence m
3
=
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
200

m
0
m
1
m
2
m’
0
m’
1
m’
2
O
m
0
m
1
m
2
m’
0
m’
1
m’
2
O
(a) (b)
Figure 1: (a) If the motions are planar, object and back-
ground trajectories belong to different 2-D affine spaces. (b)
If the motions are translational, object and background tra-
jectories belong to 2-D affine spaces that are parallel to each
other.
0 in Eq. (5). Thus, the trajectories of points under-
going the same motion are in a common “2-D affine
space” passing through m
0
and spanned by {m
1
, m
2
}
(Fig. 1(a))
If, moreover, objects and a background merely
translate without rotation, we can fix the basis vectors
i
κ
and j
κ
in the X and Y directions, respectively. This
means that the vectors m
1
and m
2
in Eq. (5) are com-
mon to all the objects and the background. Thus, the
2-D affine spaces are parallelto each other (Fig. 1(b)).
It is well known that the interaction-matrix-based
method of Costeira and Kanade (1998) fails if the mo-
tion is planar. Furthermore, if there exist two 2-D
affine spaces parallel to each other, they are both con-
tained in some 3-D affine space, and hence in some
4-D subspace. This means classification of different
motions into 3-D affine spaces or into 4-D subspaces
is impossible. Yet, this type of degeneracy is very fre-
quent in real situations. In fact, almost all “natural”
scenes in the Hopkins155 database undergo such de-
generacy to some extent
1
. This may be the main rea-
son that many researchers have regarded multibody
motion segmentation as difficult and tried various so-
phisticated mathematics one after another.
The MSL of Sugaya and Kanatani (2004) resolved
this by starting from the translational motion assump-
tion and progressivelyapplying more general assump-
tions so that any degeneracy is not untested. In this
paper, we improve their method by introducing new
analytical initial segmentation and going on to suc-
cessive upgrading in slightly different dimensions.
4 DIMENSION COMPRESSION
In the following, we concentrate on two motions: an
object is moving relative to a background, which is
1
The exceptions are the artificial “box” scenes, in which
boxes autonomously undergo unnatural 3-D translations
and rotations. For these, segmentation is very easy.
also moving. If the two motions are both general, the
observed trajectories belong to two 3-D affine spaces
in 2M-D. There exists a 7-D affine space that contains
both. Hence, segmentation of trajectories can be done
in a 7-D affine space: noise components in the out-
ward directions do not affect the segmentation. If we
translate the 7-D affine space so that it passes through
the origin, take seven basis vectors in it, and express
all the trajectories in their linear combinations, each
trajectory can be identified with a point in 7-D. Simi-
larly, if the observed trajectories are in two 2-D affine
spaces in 2M-D, there exists a 5-D affine space that
contains both. Then, each trajectory can be identified
with a point in 5-D. If, moreover, the two 2-D affine
spaces in 2M-D are parallel to each other, there exists
a 3-D affine space that contains both, and each trajec-
tory can be identified with a point in 3-D.
A trajectory in 2M-D can be identified with a point
in d-D by the following PCA (Principal Component
Analysis):
1. Compute the centroid p
C
of all the trajectories
{p
α
} and the deviations
˜
p
α
from it:
p
C
=
1
N
N
∑
α=1
p
α
,
˜
p
α
= p
α
−p
C
. (6)
2. Compute the SVD (Singular Value Decomposi-
tion) of the following 2M×N matrix in the form
˜
p
1
, ...,
˜
p
N
= Udiag(σ
1
, ..., σ
r
)V
⊤
, (7)
where r = min(2M, N), and U and V are 2M ×r
and N × r matrices, respectively, having r or-
thonormal columns.
3. Let u
i
be the ith column of U, and compute the
following d-D vectors r
α
, α = 1, ..., N:
r
α
=
(
˜
p
α
,u
1
), ..., (
˜
p
α
,u
d
)
⊤
. (8)
In this paper, we denote the inner product of vectors
a and b by (a,b).
5 INITIAL SEGMENTATION
Now, we describe our analytical initial segmentation
that replaces the heuristic clustering of MSL. We
identify trajectories with points in 3-D by the above
procedure and fit two planes (= 2-D affine spaces).
If the object and the background are both in transla-
tional motions, all the 3-D points belong to two paral-
lel planes. This may not hold if the data are noisy or
rotational components exist, but if the noise is small
and the motions are nearly translational, which is the
IMPROVED MULTISTAGE LEARNING FOR MULTIBODY MOTION SEGMENTATION
201

case in most natural scenes, we can expect that two
planes can fit to all the points fairly well.
A plane Ax+By+Cz+D = 0 in 3-D can be written
as (n,x) = 0, where we put
n = (A, B, C, D)
⊤
, x = (x, y, z, 1)
⊤
. (9)
Two planes (n
1
,x) = 0 and (n
2
,x) = 0 can be com-
bined into one in the form
(n
1
,x)(n
2
,x) = (x,n
1
n
⊤
2
x) = (x,Qx) = 0, (10)
where we define the following symmetric matrix Q:
Q =
n
1
n
⊤
2
+ n
2
n
⊤
1
2
. (11)
Note that it is a symmetric matrix that defines a
quadratic form. Equation (11) implies that Q has rank
2 with two multiple zero eigenvalues and that the re-
maining eigenvalues have different signs. Let these
eigenvalues be λ
1
, 0, 0, −λ
2
in descending order, and
u
1
, u
2
, u
3
, u
4
the corresponding unit eigenvectors.
Then, Q has the following spectral decomposition:
Q=λ
1
u
1
u
⊤
1
−λ
2
u
4
u
⊤
4
=
r
λ
1
2
u
1
+
r
λ
2
2
u
4
r
λ
1
2
u
1
−
r
λ
2
2
u
4
⊤
+
r
λ
1
2
u
1
−
r
λ
2
2
u
4
r
λ
1
2
u
1
+
r
λ
2
2
u
4
⊤
. (12)
Comparing this with Eq. (11) and noting that vectors
n
1
and n
2
(hence the matrix Q) have scale indeter-
minacy, we can determine n
1
and n
2
up to scale as
follows:
n
1
=
p
λ
1
u
1
+
p
λ
2
u
4
, n
2
=
p
λ
1
u
1
−
p
λ
2
u
4
. (13)
Let x
1
, ..., x
N
be the 3-D points that represent trajec-
tories. In the presence of noise or rotational compo-
nents, they may not exactly satisfy Eq. (10), so we fit
a quadratic surface (x, Qx) = 0 to them in such a way
that
(x
α
,Qx
α
) ≈ 0, α = 1, ...,N. (14)
Once such a Q is obtained (the computation is de-
scribed in the next section), we can determine the
vectors n
1
and n
2
that specify the two planes by
Eqs. (13). The distance d of a point (x,y,z) to a plane
Ax+ By +Cz+ D = 0 is
d =
|Ax+ By +Cz+ D|
√
A
2
+ B
2
+C
2
. (15)
For each point x
α
, we compute the distances to the
two planes and classify it to the nearer one. The re-
sulting segmentation is fed to the subsequent learning.
The above computation is a special application of
the GPCA of Vidal et al. (2005, 2008), which ex-
presses multiple subspaces as one high-dimensional
polynomial and classifies points into different sub-
spaces by fitting the high-dimensional polynomial to
all the points. Here, we classify points into two affine
spaces using the same principle.
6 HYPERSURFACE FITTING
The matrix Q that satisfies Eq. (14) is computed as
follows. In terms of the homogeneous coordinate
vector x defined in Eqs. (9), the equation (x, Qx) =
0 for a symmetric matrix Q defines a quadric sur-
face, describing an ellipsoid, a hyperboloid, an ellip-
tic/hyperbolic paraboloid, or their degeneracy includ-
ing a pair of planes. We fit a surface (x,Qx) = 0 to the
points x
α
in 3-D in the same way as we fit a conic (an
ellipse, a hyperbola, a parabola, or their degeneracy)
to points in 2-D (Kanatani and Sugaya, 2007). If we
define 9-D vectors z
α
and u by
z
α
=(x
2
α
,y
2
α
,z
2
α
,2y
α
z
α
,2z
α
x
α
,2x
α
y
α
,2x
α
,2y
α
,2z
α
)
⊤
,
v= (Q
11
,Q
22
,Q
33
,Q
23
,Q
31
,Q
12
,Q
41
,Q
42
,Q
43
)
⊤
, (16)
Eq. (14) is rewritten as
(z
α
,v) + Q
44
≈ 0, α = 1,...,N. (17)
A well known method for computing such v and
Q
44
is the method of Taubin (1991), which is known
to be highly accurate as compared with naive least
squares (Kanatani, 2008; Kanatani and Sugaya 2007).
Theoretically, ML (Maximum Likelihood) achieves
higher accuracy (Kanatani, 2008; Kanatani and Sug-
aya, 2007), but the surface (x,Qx) = 0 that degener-
ates into two planes has singularities along their inter-
section. We have observed that iterations for ML fail
to converge when some data points are near the singu-
larities; the corresponding denominators diverge and
become ∞ if they coincide with singularities
2
.
The Taubin method in this case goes as follows.
Assume that x
α
, y
α
, and z
α
are perturbed by Gaussian
noise ∆x
α
, ∆y
α
, and ∆z
α
, respectively, of mean 0 and
standard deviation σ. Let ∆z
α
be the perturbation of
z
α
in Eqs. (16). By first order expansion, we have
∆z
α
=(2x
α
∆x
α
,2y
α
∆y
α
,2z
α
∆z
α
,2∆y
α
z
α
+ 2y
α
∆z
α
,
..., 2∆z
α
)
⊤
, (18)
from which we can evaluate the covariance matrix
V[z
α
] = E[∆z
α
∆z
⊤
α
] of z
α
. Noting the relations E[∆x
α
]
= E[∆y
α
] = E[∆z
α
] = 0, E[∆y
α
∆z
α
] = E[∆z
α
∆x
α
] =
E[∆x
α
∆y
α
] = 0, and E[∆x
2
α
] = E[∆y
2
α
] = E[∆z
2
α
] = σ
2
,
we obtain V[z
α
] = σ
2
V
0
[z
α
], where
V
0
[z
α
] =
x
2
α
0 0 0 z
α
x
α
x
α
y
α
x
α
0 0
∗ y
2
α
0 y
α
z
α
0 x
α
y
α
0 y
α
0
∗ ∗ z
2
α
y
α
z
α
z
α
x
α
0 0 0 z
α
∗ ∗ ∗ y
2
α
+ z
2
α
x
α
y
α
z
α
x
α
0 z
α
y
α
∗ ∗ ∗ ∗ z
2
α
+ x
2
α
y
α
z
α
z
α
0 x
α
∗ ∗ ∗ ∗ ∗ x
2
α
+ y
2
α
y
α
x
α
0
∗ ∗ ∗ ∗ ∗ ∗ 1 0 0
∗ ∗ ∗ ∗ ∗ ∗ ∗ 1 0
∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ 1
. (19)
2
ML minimizes the sum of the distances, measured in
the direction of the surface normals, to the surface, but no
surface normals can be defined at singularities.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
202

Here, ∗ means copying the element in the sym-
metric position. The Taubin method minimizes
J
T
=
∑
N
α=1
(z
α
,v) + Q
44
2
∑
N
α=1
(v,V
0
[z
α
]v)
. (20)
If the denominator is omitted, this becomes the naive
least squares, but the existence of the denominator is
crucial for improving the accuracy as we show later.
The solution {v, Q
44
} that minimizes Eq. (20) is ob-
tained as follows (Kanatani and Sugaya, 2007):
1. Compute the centroid z
C
of {z
α
} and the devia-
tions
˜
z
α
from it:
z
C
=
1
N
N
∑
α=1
z
α
,
˜
z
α
= z
α
−z
C
. (21)
2. Compute the following 9×9 matrices:
M
T
=
N
∑
α=1
˜
z
α
˜
z
⊤
α
, N
T
=
N
∑
α=1
V
0
[z
α
]. (22)
3. Solve the generalized eigenvalue problem
M
T
v = λN
T
v, (23)
and compute the unit generalized eigenvector v
for the smallest generalized eigenvalue λ.
4. Compute Q
44
as follows:
Q
44
= −(z
C
,v). (24)
7 MULTISTAGE LEARNING
After an initial segmentation is obtained, we fit affine
spaces by the EM algorithm in successively higher di-
mensions:
1. Two parallel panes in 3-D.
2. Two 2-D affine spaces in 5-D.
3. Two 3-D affine spaces in 7-D.
If the object and the background are in transla-
tional motions, an optimal solution is obtained in the
first stage, and it is still optimal in the second and the
third stages. If the object and the backgroundundergo
planar motions with rotations, an optimal solution is
obtained in the second stage, and it is still optimal in
the third. If the object and the background are in gen-
eral 3-D motions, an optimal solution is obtained in
the third stage. Because a degenerate motion is a spe-
cial case of general motions, an optimal solution for
a degenerate motion is unchanged when optimized by
assuming a more general motion. This is the basic
principle of MSL of Sugaya and Kanatani (2004).
The EM algorithm for classifying n-D points r
α
,
α = 1, ..., N, into two d-D affine spaces (n ≥ 2d + 1)
is as follows:
1. Using the initial classification, define the mem-
bership weight W
(k)
α
of r
α
to class k (= 1, 2) as
follows
W
(k)
α
=
1 if r
α
belongs to class k
0 otherwise
. (25)
2. For each class k (= 1, 2), do the following compu-
tation:
(a) Compute the prior w
(k)
of class k as follows.
w
(k)
=
1
N
N
∑
α=1
W
(k)
α
. (26)
(b) If w
(k)
≤ d/N, stop (the number of points is too
small to span a d-D affine space).
(c) Compute the centroid r
(k)
C
of class k:
r
(k)
C
=
∑
N
α=1
W
(k)
α
r
α
∑
N
α=1
W
(k)
α
. (27)
(d) Compute the moment M
(k)
of class k:
M
(k)
=
∑
N
α=1
W
(k)
α
(r
α
−r
(k)
C
)(r
α
−r
(k)
C
)
⊤
∑
N
α=1
W
(k)
α
.
(28)
Let λ
(k)
1
≥ ··· ≥ λ
(k)
n
be the n eigenvalues of
M
(k)
, and u
(k)
1
, ..., u
(k)
n
the corresponding unit
eigenvectors.
(e) Compute the “inward” projection matrix P
(k)
onto class k and the “outward” projection ma-
trix P
(k)
⊥
onto the space orthogonal to it by
P
(k)
=
d
∑
i=1
u
(k)
i
u
(k)⊤
i
, P
(k)
⊥
= I−P
(k)
. (29)
3. Estimate the square noise level σ
2
from the square
sum of the “outward” noise components in the
form
ˆ
σ
2
=min[
N
(n−d)(N −d −1)
tr(w
(1)
P
(1)
⊥
M
(1)
P
(1)
⊥
+w
(2)
P
(2)
⊥
M
(2)
P
(2)
⊥
),σ
2
min
], (30)
where tr denotes the trace, and σ
min
is a small
number, say 0.1 pixels, to prevent
ˆ
σ
2
from becom-
ing exactly 0, which would cause computational
failure in the subsequent computation, The num-
ber (n −d)(N −d −1) accounts for the degree of
freedom of the χ
2
-distribution of the square sum
of the “outward” noise components (Kanatani,
1996).
IMPROVED MULTISTAGE LEARNING FOR MULTIBODY MOTION SEGMENTATION
203
4. Compute the covariance matrix V
(k)
of class k (=
1, 2) as follows:
V
(k)
= P
(k)
M
(k)
P
(k)
+
ˆ
σ
2
P
(k)
⊥
. (31)
The first term on the right-hand side is for the data
variations within the affine space; the second ac-
counts for the “outward” noise components.
5. Do the following computation for each point r
α
,
α = 1, ..., N:
(a) Compute the conditional likelihood P(α|k), k =
1, 2, of r
α
by
P(α|k) =
e
−(r
α
−r
(k)
C
,V
(k)−1
(r
α
−r
(k)
C
))/2
√
detV
(k)
. (32)
(b) Update the membership weight W
(k)
α
, k = 1, 2,
of r
α
as follows:
W
(k)
α
=
w
(k)
P(α|k)
w
(1)
P(α|1) + w
(2)
P(α|2)
. (33)
6. Go back to Step 2 and iterate the computation un-
til {W
(k)
α
} converges.
7. After convergence (or interruption), classify each
r
α
to the class k for which W
(k)
α
, k = 1, 2, is larger.
If we let n = 5 and d = 2, the above procedure is
the second stage of the multistage learning, and if we
let n = 7 and d = 3, it is the third stage. The first stage
requires an additional constraint that the two planes be
parallel. For this, we let n = 3 and d = 2 and compute
from the two matrices M
(k)
, k = 1, 2, their weighted
average
M = w
(1)
M
(1)
+ w
(2)
M
(2)
. (34)
Let λ
1
≥ ··· ≥ λ
n
be its n eigenvalues, and u
1
, ...,
u
n
the corresponding unit eigenvectors. We let the
projection matrices P
(k)
and P
(k)
⊥
coincide in the form
P
(1)
= P
(2)
= P and P
(1)
⊥
= P
(2)
⊥
= P
⊥
, where
P =
d
∑
i=1
u
i
u
⊤
i
, P
⊥
= I−P. (35)
The estimation of the square noise level σ
2
in Step 3
is replaced by
ˆ
σ
2
= min[
N
(n−d)(N −d −2)
tr(P
⊥
MP
⊥
),σ
2
min
].
(36)
The rest is unchanged.
However, there is an inherent problem in EM-
based learning: If there is no noise, its distribution
cannot be stably estimated. This causes no problem
in real situations but may result in computational fail-
ure when ideal data are used for a testing purpose.
(a)
0
1
2
3
2 4 6 8 10
σ
0
2 3
1
(b)
0
1
2
3
2 4 6 8 10
0
1
2
3
σ
(c)
0
1
2
3
2 4 6 8 10
σ
0
1
2
3
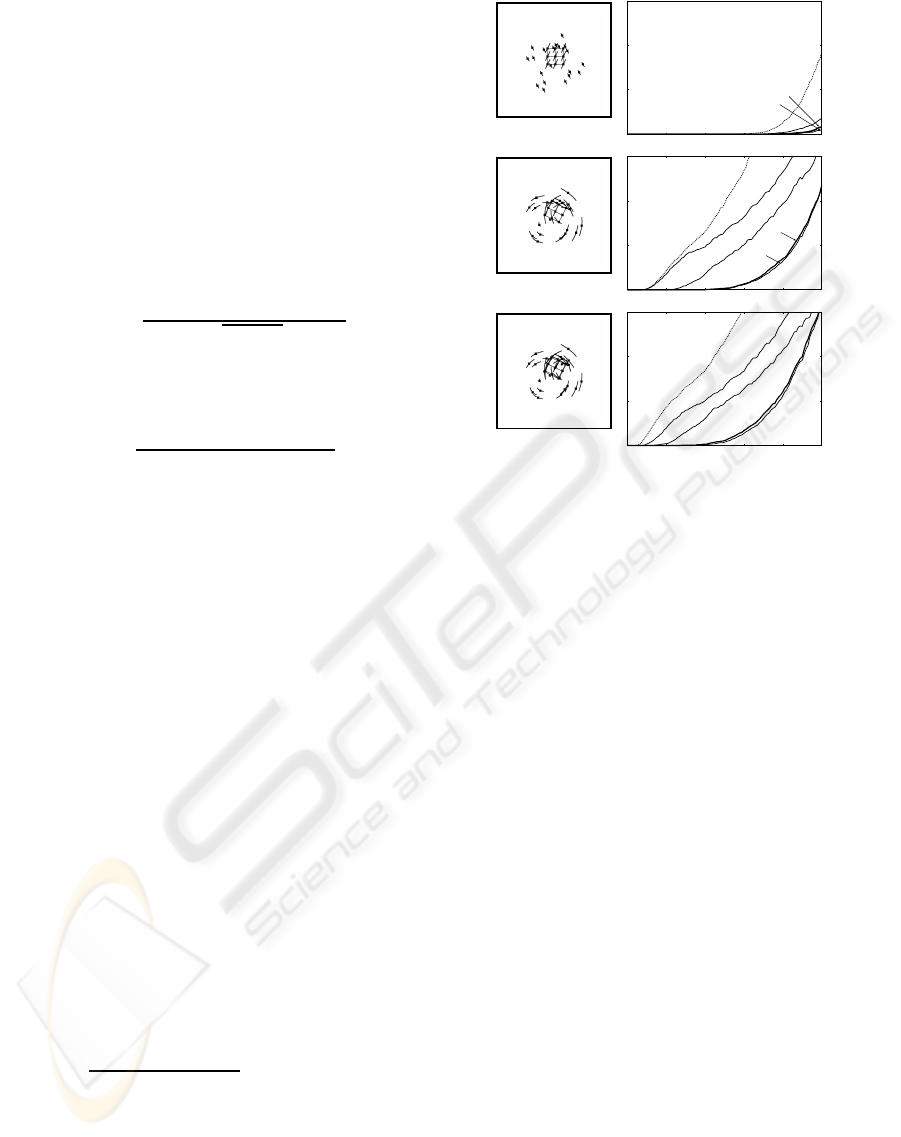
Figure 2: Left column: 20 background points and 14 ob-
ject points. (a) Translational motion. (b) Planar motion. (c)
General 3-D motion. Right column: Average misclassifi-
cation ratio over 5000 trials. The horizontal axis is for the
standard deviation σ of added noise. 0) Initial segmentation
by the Taubin method. 1) Parallel plane fitting in 3-D. 2)
2-D affine space fitting in 5-D. 3) 3-D affine space fitting in
7-D. The dotted lines are for initial segmentation by least
squares.
This phenomenon was reported by Tron and Vidal
(2007) for MSL. In the above procedure, this occurs
when points are exactly in a 2-D affine space in 7-D,
in which case the covariance matrix degenerates to
have rank 2 and hence the likelihood cannot be de-
fined: To define P(α|k), the matrix V
(k)
in Eq. (31)
must have rank n, and detV
(k)
in the denominator of
Eq. (32) must be positive. To cope with this, our sys-
tem checks if such a degeneracy exists by using the
geometric AIC (Kanatani, 1996), and if so judged, the
3-D affine space is replaced by a 2-D affine space (we
omit the details). Such a treatment does not affect the
performance when real data are used.
8 EXPERIMENTS
8.1 Simulation
The left column of Fig. 2 shows simulated 512×512-
pixel images of 14 object points and 20 background
points in (a) translational motion, (b) planar motion,
and (c) general 3-D motion. These are the 5th of 10
frames; the curves in them are trajectories over the
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
204
(a) (b) (c)
Figure 3: 3-D visualization of image motions in Fig. 2.
10 frames. We added Gaussian noise of mean 0 and
standard deviation σ to the x and y coordinates of each
point in each frame independently, and evaluated the
average misclassification ratio over 5000 independent
trials for each σ. The result is shown in the right col-
umn. The plots 0 – 3 correspond to the initial seg-
mentation by the Taubin method, parallel plane fitting
in 3-D, 2-D affine space fitting in 5-D, and 3-D affine
space fitting in 7-D, respectively. For comparison, we
plot in dotted lines the initial segmentation we would
obtain if naive least squares were used.
We can observe that for the translational motion
(a), the initial segmentation is already correct enough;
an almost complete segmentation is obtained in the
first stage. For the planar motion (b), we obtain an
almost correct segmentation in the second stage, and
for the general 3-D motion in the third. We can also
confirm that the Taubin method (plots 0) for initial
segmentation is more accurate than the naive least
squares (dotted lines).
Figure 3 shows motion trajectories compressed to
3-D by Eq. (13) (d = 3) viewed from a particular an-
gle. For the translational motion (a), all the points
belong to two parallel planes, as predicted. For the
planar motion (b) and the general 3-D motion (c), the
points still belong to nearly parallel and nearly planar
surfaces. This fact explains the high performance of
our Taubin initial segmentation.
8.2 Real Video Experiments
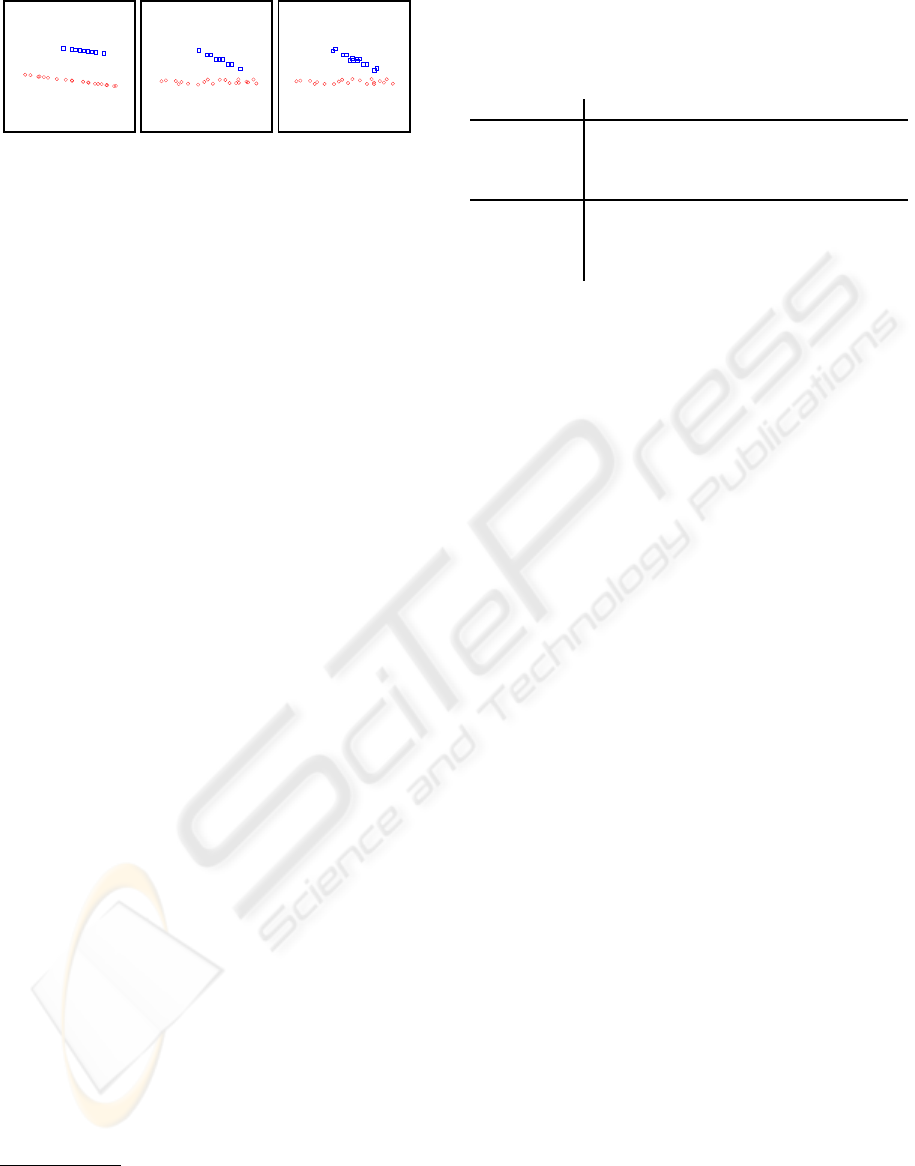
The upper row of Fig. 4 shows six videos from the
Hopkins155 database
3
(Tron and Vidal, 2007). The
lower row shows our 3-D visualization of the trajec-
tories. Table 1 lists the correct classification ratios at
each stage of our method
4
and some others: the MSL
of Sugaya and Kanatani
5
(2004); the method of Vidal
et al.
6
(Vidal et al., 2005); RANSAC
5
; the method
of Yan and Pollefeys
5
(2006). We can see that for all
the videos, our method reach high classification ratios
in relatively early stages and 100% in the end, while
3
http://www.vision.jhu.edu/data/hopkins155
4
http://www.iim.cs.tut.ac.jp/˜sugaya/public-e.html
5
The code is at the cite in the footnote 4.
6
We used the code placed at the cite in footnote 3.
Table 1: Correct classification ratios (%) for the data in
Fig. 4 in each stage of our method, and comparisons with
other methods: MSL of Sugaya and Kanatani (2004), Vi-
dal et al. (2005, 2008), RANSAC, and Yan and Pollefeys
(2006).
(a) (b) (c) (d) (e) (f)
Initial 88.8 99.1 98.0 100.0 100.0 98.6
1st stage 99.7 99.6 100.0 100.0 100.0 100.0
2nd stage 98.8 99.6 100.0 100.0 100.0 100.0
3rd stage 100.0 100.0 100.0 100.0 100.0 100.0
MSL 99.7 99.6 100.0 100.0 100.0 100.0
Vidal et al. 88.2 99.6 99.2 99.4 100.0 100.0
RANSAC 91.8 99.6 96.6 97.5 100.0 100.0
Yan-Pollefeys 98.5 98.2 97.4 94.3 99.8 80.8
other methods do not necessarily achieve 100%. This
is because we focus on the motion type and take de-
generacies into account, while other methods do not
pay so much attention to them. As the bottom row
of Fig. 4 shows, even when the visible motions look
complicated, it is common for the trajectories to be in
nearly parallel planes. The high performance of our
method is based on this observation.
9 CONCLUSIONS
We presented an improved version of the MSL of
Sugaya and Kanatani (2004). First, we replaced their
initial segmentation based on heuristic clustering us-
ing the interaction matrix of Costeira and Kanade
(1998) and the geometric AIC (Kanatani, 1996) by an
analytical computation based on the GPCA of Vidal et
al. (2005, 2008), fitting two 2-D affine spaces in 3-D
by the method of Taubin (1991). The resulting initial
segmentation alone can segment most of the motions
we frequently encounter in natural scenes fairly cor-
rectly, and the result is successively optimized by the
EM algorithm in 3-D, 5-D, and 7-D. Using simulated
and real videos, we demonstrated that our method be-
haves as predicted and illustrated the mechanism un-
derneath using our visualization technique. This is a
big contrast to all existing methods, whose behavior
is difficult to predict unless tested using a particular
database.
ACKNOWLEDGEMENTS
The authors thank R´ene Vidal of Johns Hopkins Uni-
versity for helpful discussions. This work was sup-
ported in part by the Ministry of Education, Culture,
Sports, Science, and Technology, Japan, under Grant
in Aid for Scientific Research (C 21500172) and for
Young Scientists (B 18700181).
IMPROVED MULTISTAGE LEARNING FOR MULTIBODY MOTION SEGMENTATION
205

24 frames
330 points
29 frames
225 points
30 frames
502 points
31 frames
159 points
30 frames
469 points
100 frames
73 points
(a) (b) (c) (d) (e) (f)
Figure 4: Top: Feature points detected from 6 video streams of the Hopkins155 database. Bottom: Their their 3-D represen-
tation.
REFERENCES
Costeira, J. P. and Kanade, T. (1998). A multibody factor-
ization method for independently moving objects, Int.
J. Computer Vision, 29, 159–179.
Fan, Z., Zhou, J. and Wu, Y. (2006). Multibody grouping
by inference of multiple subspace from high-
dimensional data using oriented-frames, IEEE Trans
Patt. Anal. Mach. Intell., 28, 91–105.
Gear, C. W. (1998). Multibody grouping from motion im-
ages, Int. J. Comput. Vision, 29, 133–150.
Ichimura, N. (1999). Motion segmentation based on fac-
torization method and discriminant criterion, Proc. 7th
Int. Conf. Comput. Vis., Vol. 1, Kerkyra, Greece, 600–
605.
Ichimura, N. (2000). Motion segmentation using feature
selection and subspace method based on shape space,
Proc. 15th Int. Conf. Pattern Recog., Vol. 3, Barcelona,
858–864.
Inoue, K. and Urahama, K. (2001). Separation of multiple
objects in motion images by clustering, Proc. 8th Int.
Conf. Comput. Vis., Vol. 1, Vancouver, 219–224.
Kanatani, K. (2002a). Evaluation and selection of models
for motion segmentation, Proc. 7th Euro. Conf. Com-
put. Vis., Vol. 3, Copenhagen, 335–349.
Kanatani, K. (2001). Motion segmentation by subspace
separation and model selection, Proc. 8th Int. Conf.
Comput. Vis., Vol. 2, Vancouver, 301–306.
Kanatani, K. (2002b). Motion segmentation by subspace
separation: Model selection and reliability evaluation,
Int. J. Image Graphics, 2, 179–197.
Kanatani, K. (1996). Statistical Optimization for Geomet-
ric Computation: Theory and Practice, Amsterdam:
Elsevier. Reprinted (2005) New York: Dover.
Kanatani, K. (2008). Statistical optimization for geometric
fitting: Theoretical accuracy analysis and high order er-
ror analysis, Int. J. Comput. Vision, 80, 167–188.
Kanatani, K. and Sugaya, Y. (2007). Performance evalua-
tion of iterative geometric fitting algorithms, Comp.
Stat. Data Anal., 52, 1208–1222.
Poelman, C. J. and Kanade, T. (1997). A paraperspective
factorization method for shape and motion recovery,
IEEE Trans. Pattern Anal. Mach. Intell., 19, 206–218.
Rao, S. R., Tron, R., Vidal R. and Ma, Y. (2008). Motion
segmentation via robust subspace separation in the
presence of outlying, incomplete, or corrupted trajec-
tories, Proc. IEEE Conf. Comput. Vision Patt. Recog.,
Anchorage, AK.
Schindler, K., Suter, D. and Wang, H. A model-selection
framework for multibody structure-and-motion of
image sequences, Int. J. Comput. Vision, 79, 159–177.
Sugaya, Y. and Kanatani, Y. (2004). Multi-stage optimiza-
tion for multi-body motion segmentation. IEICE Trans.
Inf. & Syst., E87-D, 1935–1942.
Taubin, G. (1991). Estimation of planer curves, surfaces,
and non-planar space curves defined by implicit equa-
tions with applications to edge and range image seg-
mentation, IEEE Trans. Patt. Anal. Mach. Intell., 13,
1115–1138.
Tomasi, C. and Kanade, T. (1992). Shape and motion from
image streams under orthography—A factorization
method, Int. J. Comput. Vision, 9, 137–154.
Tron, R. and Vidal, R. (2007). A benchmark for the com-
parison of 3-D motion segmentation algorithms, Proc.
IEEE Conf. Comput. Vision Patt. Recog., Minneapolis,
MN.
Vidal, R., Ma, Y. and Sastry, S. (2005). Generalized prin-
cipal component analysis (GPCA), IEEE Trans. Patt.
Anal. Mach. Intell., 27, 1945–1959.
Vidal, R. Tron, R. and Hartley, R. (2008). Multiframe mo-
tion segmentation with missing data using PowerFac-
torization and GPCA, Int. J. Comput. Vision, 79, 85–
105.
Wu, Y. Zhang, Z., Huang, T. S. and Lin, J. Y. (2001).
Multibody grouping via orthogonal subspace decom-
position, sequences under affine projection, Proc.
IEEE Conf. Computer Vision Pattern Recog., Vol. 2,
Kauai, HI, 695–701.
Yan, J. and Pollefeys, M. (2006). A general framework for
motion segmentation: Independent, articulate, rigid,
non-rigid, degenerate and nondegenerate, Proc. 9th
Euro. Conf. Comput. Vision., Vol. 4, Graz, Austria,
94–104.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
206
