VECTOR SEGMENTATION OF VOLUMETRIC IMAGE DATA

Tetrahedral Meshing Constrained by Image Edges

Michal

Span

el, P

remysl Kr

sek, Miroslav

Svub and V

ıt

Stancl

Department of Computer Graphics and Multimedia

Faculty of Information Technology, Brno University of Technology, Czech Republic

Keywords:

CT/MR data, Medical image segmentation, Surface reconstruction, Delaunay triangulation, Variational tetra-

hedral meshing, Isotropic meshing, Graph-cut segmentation.

Abstract:

In this paper, a vector segmentation algorithm of volumetric data based on the 3D Delaunay triangulation is

presented. A modiﬁed variational meshing method is used to adapt tetrahedral mesh to the underlying CT/MRI

volumetric data. Moreover, to classify tetrahedra in the mesh into regions whose characteristics are similar,

a clustering scheme viewing the mesh as undirected graph with edges weighted according to similarity of

tetrahedra is discussed.

1 INTRODUCTION

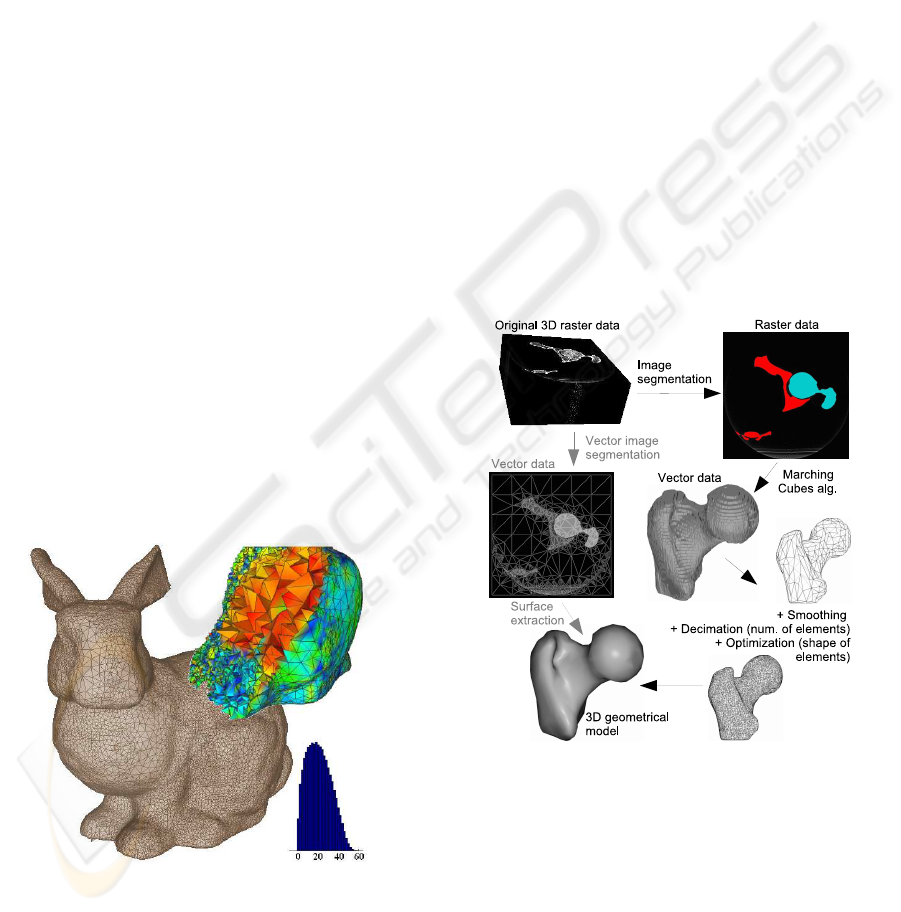
Traditional raster-based segmentation methods pro-

duce data which are not suitable for geometrical 3D

modeling. Most often, an algorithm such as March-

ing Cubes (Lorensen and Cline, 1987) is applied to

reconstruct surfaces from the raster data. Therewith,

further decimation and smoothing of the model are

required.

Figure 1: Result of the proposed tetrahedral meshing

method, and histogram of the minimal dihedral angles in

the ﬁnal mesh. The bunny was printed using rapid proto-

typing machine (3D printer) and scanned on a CT machine.

Afterwards, the volumetric data was processed.

Principal task of an image segmentation is the im-

Figure 2: Comparison of the traditional raster-based seg-

mentation (black labeling) and the presented vector seg-

mentation method (gray).

age partitioning into a set of non-overlapping regions

so that variation of some property within each region

follows a simple model. It has been shown that 2D

Delaunay triangulation can be used to effectively par-

tition the image (Gevers, 2002), while the mesh is

adapted to the image structure by combining region

and edge information.

In this paper, recent advances in a vector segmen-

134

Spanel M., Krsek P., Svub M. and Stancl V. (2010).

VECTOR SEGMENTATION OF VOLUMETRIC IMAGE DATA - Tetrahedral Meshing Constrained by Image Edges.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 134-138

DOI: 10.5220/0002833201340138

 SciTePress

tation technique based on a 3D Delaunay Triangula-

tion are presented. This work follows principles pre-

viously described in (Spanel et al., 2007). Tetrahedral

mesh is used to partition volumetric image data into

regions (see Figure 2). Process of the mesh construc-

tion respects signiﬁcant image edges, so surfaces of

image regions are well described and can be easily

derived.

2 TETRAHEDRAL MESHING

A mesh generation (George and Borouchaki, 1998)

aims at tessellation of a bounded 3D domain Ω with

tetrahedra. Algorithms for 3D mesh generation have

been intensively studied over the last years. Basi-

cally, three main families of algorithms have been de-

scribed: Octree methods, Advancing front methods,

and Delaunay-based methods (Owen, 1998).

2.1 Delaunay Triangulation (DT)

Every tetrahedron of the DT satisﬁes the Delaunay

criterion. This criterion means that circumsphere as-

sociated with the tetrahedron does not contain any

other vertices. This criterion is a characterization of

the Delaunay triangulation. The Delaunay triangula-

tion generates regularly shaped tetrahedra and is very

attractive from a robustness point of view due to sim-

plicity of the Delaunay criterion.

Constrained Delaunay triangulation (CDT) is a

triangulation where constraints given as set of edges

and faces in 3D remain as entities of the resulting

mesh. There are two classes of methods depending on

how the constraints must be satisﬁed. The ﬁrst kind

acts by local modiﬁcations to enforce the given con-

straints, while the other kind tends to modify the con-

straints and creates an admissible set of constraints.

A Constraint partitioning method is a simple rep-

resentative of the second class. Every tetrahedron in-

tersected by a constrained edge/face is divided ensur-

ing that the created sub-edges are in the resulting tri-

angulation. Advantage of the constraint partitioning

method is that it can be easily extended to 3D.

Many Delaunay reﬁnement methods (Shewchuk,

2002) exist that improve tetrahedra locally by insert-

ing new nodes to maintain the Delaunay criterion.

2.2 Isotropic Meshing

Many applications have speciﬁc requirements on the

size and shape of elements in the mesh. The aim of the

isotropic meshing is to locate vertices so that the re-

sulting mesh consists of almost equilateral tetrahedra.

In addition, the element size is close to a predeﬁned

size constraint.

One of the existing methods to create vertices in

accordance with the size speciﬁcations, creation of

points along the edges, is discussed in (George and

Borouchaki, 1998). The idea is to create new points

along existing edges in the triangulation and obtain

nearly equilateral tetrahedra having edges of length h.

In (Spanel et al., 2007), this method has been modi-

ﬁed for isotropic meshing of volumetric image data.

2.3 Variational Tetrahedral Meshing

Many approaches based on energy minimization (Du

and Wang, 2003) have been proposed as a powerful

tool in meshing. In this paper, a vector segmentation

technique, built upon a Variational Tetrahedral Mesh-

ing approach (Alliez et al., 2005), is presented. A

simple minimization procedure alternates two steps:

• Delaunay triangulation optimizing connectivity,

• local vertex relocation,

to consistently and efﬁciently minimize a global en-

ergy over the domain. It results in a robust meshing

technique that generates high quality meshes in terms

of radius ratios as well as angles.

To extend the approach to allow isotropic mesh-

ing, the sizing ﬁeld H is introduced A mass density

in space can be deﬁned and used in computation of

the optimal vertex position. This density should agree

with the sizing ﬁeld. Alliez uses a one-point approxi-

mation of the sizing ﬁeld in a tetrahedron. In geomet-

ric terms, an optimal position of the interior vertex X

in its 1-ring can be expressed as:

∗

∑

∈Ω

)

∑

∈Ω

)

. (1)

where G

is the centroid of tetrahedron T

In (Alliez et al., 2005), a default sizing ﬁeld is

proposed, robust for a large spectrum of mesh types.

Deﬁnition of the sizing ﬁeld is build on the notion of

local feature size that corresponds to the combination

of domain boundary curvature and thickness as well.

The local feature size l fs(P) at a point P of do-

main boundary is deﬁned as the distance d(P, S(Ω))

to a medial axis S(Ω). The medial axis, or skeleton,

is the locus of all centers of maximal balls inscribed

in the boundary. Given the local feature size on the

boundary, we need a controllable way to extrapolate

this function to the interior. The function

= min

S∈δΩ

[Kd(P) + l fs(S)] (2)

satisﬁes this criterion. The parameter K controls gra-

dation of the resulting ﬁeld.

VECTOR SEGMENTATION OF VOLUMETRIC IMAGE DATA Tetrahedral Meshing Constrained by Image Edges

135

3 DELAUNAY-BASED VECTOR

SEGMENTATION

Based on the introduced principles, the vector seg-

mentation was originally proposed as follows:

1. 3D edge and corner detection - Candidate vertices

lying on regions boundaries, meaningful edges

and corners are located.

2. Initial Delaunay triangulation - Tetrahedral mesh

is constructed from the sampled set of can-

didate vertices by the common Incremental

Method (George and Borouchaki, 1998).

3. Iterative adaptation - The triangulation is adapted

to the underlying image structure.

4. Mesh segmentation - Classiﬁcation of tetrahedra

into image regions.

This paper introduces several changes in the orig-

inal segmentation. The mesh of the DT is adapted to

the image structure by means of isotropic edge split-

ting and variational meshing. The image is classiﬁed

into regions using a graph-based clustering algorithm.

3.1 3D Edge and Corner Detection

The triangulation starts with a set of candidate ver-

tices distributed over the entire image. In all our ex-

periments, the well known Canny edge detector ex-

tended to the 3D space has been used.

In order to respect signiﬁcant features in the volu-

metric data during the meshing, we have modiﬁed the

Susan corner detector (Smith and Brady, 1996) ex-

tending its functionality into 3D space. The Susan

(Smallest Univalue Segment Assimilating Nucleus)

detector was originally developed to locate feature

points in 2D images.

Analogous to Smith and Brady, the modiﬁed 3D

SUSAN places a spherical mask R over the voxel to

be tested (the nucleus). The voxel in this mask is rep-

resented by v ∈ R. The nucleus is at v

. Every voxel is

compared to the nucleus using a distance function c

Final response of the SUSAN detector is proportional

to an area n(R) of the SUSAN given by:

n(R) =

∑

∈R

. (3)

In the equation (3), N is the number of voxels within

a spherical mask R used as a normalization factor. If

is the rectangular function, then the previously de-

ﬁned area represents the number of voxels in the mask

having brightness similar to the nucleus.

Figure 3: Sampled initial set of vertices found by the edge

and corner detection.

3.2 Iterative Adaptation

Fundamental part of the proposed segmentation

method is adaptation of the mesh to cover the under-

lying image structure. Following two main steps are

repeated several times:

1. Isotropic edge splitting - creation of points along

existing edges, introduces new points to the mesh.

2. Variational meshing - optimization of the tessel-

lation grid by means of vertex moving.

Isotropic Edge Splitting. In this phase, the isotropic

meshing algorithm creating new points along existing

edges and another well known technique of tetrahe-

dral mesh optimization, splitting of maximal/longest

edge, are combined together. The splitting phase is

similar to the one described in (Spanel et al., 2007).

The only difference is deﬁnition of the sizing ﬁeld, so

called control space.

The control space prescribes length of edges in

the mesh. In our case, control space enforces cre-

ation of larger tetrahedra inside image regions and

smaller ones along region boundaries (image edges).

Apparently, deﬁnition of the sizing ﬁeld strongly af-

fects quality of the ﬁnal mesh.

In this sense, one can deﬁne the control space

H(Ω) in the same way as the sizing ﬁeld given by the

equation (2). This deﬁnition is robust and produces

high quality meshes. Instead of the conventional do-

main boundary, we deﬁne the control space to respect

found image edges. Thus, we generate the control

space differently:

1. Estimate distance transform from all detected im-

age edges ﬁrst.

2. Find local maxima of the distance transform in or-

der to identify medial axis.

3. Evaluate local feature size l f s(P) on image

edges using inverse distance transform propagat-

ing value from the medial axis.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

136

4. Generate control space distributing l f s(P) from

edges using the formula (2).

This sizing ﬁeld is relative. It describes the

inhomogeneity of required edge length. The real

edge length is proportional to this relative value, and

depending on the prescribed number of vertices.

Variational Meshing. The variational meshing

phase, alternating connectivity and geometry opti-

mization, is an important part of the algorithm. The

energy is minimized by moving each interior vertex

to its optimal position. Further, the energy is mini-

mized by computing the 3D Delaunay triangulating

of these new sites.

Analogous to (Alliez et al., 2005), the boundary

vertices are treated differently. In order to identify

the current boundary vertices, each voxel V

lying on

an image edge is examined. Its nearest vertex S

the mesh is located, and the distance d(V

, S

) as well

as the coordinates of V

(multiplied by the distance

d) are accumulated at that vertex. To deal with cor-

ner points, the distance d is weighted according to

the point type. Corner points have the weight signiﬁ-

cantly greater than edge points, thus the closest vertex

is attracted directly in place of the image corner.

Figure 4: Result of the adaptation of the mesh (K = 0.8).

Afterwards, all vertices with a non-zero distance

sum are the desired boundary vertices. These vertices

are moved to the average value they each have accu-

mulated during the pass over all edge voxels.

3.3 Mesh Segmentation

Every tetrahedron t

of the mesh is characterized by

its feature vector. Individual features detail image

structure of the tetrahedron and its close neighbour-

hood. In fact, the ﬁrst two components are mean pixel

value and intensity variance of voxels inside the tetra-

hedron, other features may cover image texture.

Topology of the tetrahedral mesh is suitable for

graph-based segmentation techniques. Instead of pix-

els and the traditional 4– and 8– pixel connectedness,

tetrahedra and graph adjacency are incorporated.

Graph-based Segmentation. Viewing the mesh as

undirected graph, with edges weighted according to

similarity of feature vectors, allows one to use graph

algorithms (graph cuts, path algorithms, etc.) for the

segmentation.

In our experiments, we have used the Min-

Cut/Max-Flow algorithm proposed in (Boykov and

Kolmogorov, 2004) to cut a graph whose edges are

evaluated according to the similarity of two adjacent

tetrahedra.

4 RESULTS AND DISCUSSION

The proposed segmentation algorithm was tested on a

real CT imaging data (about 120− 150 slices, resolu-

tion 512x512 pixels per slice). The whole segmenta-

tion process, including iterative mesh adaptation and

ﬁnal classiﬁcation, takes approximately 15− 25 min-

utes on standard PC with Intel DualCore 2.54GHz

processor depending on concrete number of slices,

and parameters of the meshing algorithm.

Results of the segmentation shown in Figure 5

outperforms the original method (Spanel et al., 2007).

Especially, the overall mesh quality in the sense of

shape of tetrahedra has been improved. In the Fig-

ure 5, histograms show distribution of the minimal di-

hedral angles within regions of the tetrahedral mesh.

The graph-based mesh segmentation algorithm

designed for the unsupervised clustering of feature

vectors performs almost same, sometimes slightly

better, then the original method based on Fuzzy C-

means and GMM+EM clustering techniques. Further

improvement of the classiﬁcation phase must incorpo-

rate more sophisticated image features modeling 3D

texture and spatial image properties.

An inconvenience of the described meshing tech-

nique is that slivers appear in the mesh, especially

close to the image edges. Regarding recent research

in this area, methods like the modiﬁed sliver exuda-

tion (Cheng et al., 1999), or sliver perturbation must

be incorporated in the meshing process in the future.

5 CONCLUSIONS

In this paper, the vector segmentation algorithm

based on isotropic Delaunay triangulation proposed

in (Spanel et al., 2007) is extended. To improve qual-

ity of the tetrahedral mesh, the variational meshing

is utilized. Instead of original clustering techniques,

the graph-cut algorithm is used to classify tetrahedra

VECTOR SEGMENTATION OF VOLUMETRIC IMAGE DATA Tetrahedral Meshing Constrained by Image Edges

137

a) b)

Figure 5: Result of the vector segmentation. Polygonal surfaces of meaningful image regions were extracted directly from the

classiﬁed tetrahedral mesh: soft tissues (a), hard tissues (b).

into individual regions. Both modiﬁcations have im-

proved quality of the output mesh without signiﬁcant

increase of runtime. Besides, there is still space for

improvement. It is necessary to deal with slivers, and

more sophisticated image features might be incorpo-

rated into the mesh classiﬁcation.

In general, this concept of the volumetric im-

age segmentation has several advantages. Tetrahe-

dral representation of image regions provides con-

tinuous approximation of region boundaries (image

edges), while the process of raster data vectorization

is eliminated. Moreover, a more effective representa-

tion of the image structure is obtained. Mesh structure

decreases complexity of any classiﬁcation algorithm

that processes a reduced number of tetrahedra instead

of voxels.

ACKNOWLEDGEMENTS

The authors were supported by the Faculty of

Information Technology, BUT under project no.

MSM0021630528 CZ, and CESNET association un-

der project no. MSM6383917201 CZ.

REFERENCES

Alliez, P., Cohen-Steiner, D., Yvinec, M., and Desbrun, M.

(2005). Variantional tetrahedral meshing. ACM Trans.

Graph., 24(3):617–625.

Boykov, Y. and Kolmogorov, V. (2004). An experimental

comparison of min-cut/max-ﬂow algorithms for en-

ergy minimization in vision. In IEEE Transactions

on PAMI, 26(9):1124–1137.

Cheng, S. W., Dey, T. K., Edelsbrunner, H., Facello, M. A.,

and Teng, S. H. (1999). Sliver exudation. In In Proc.

15th ACM Symp. Comput. Geom., pages 1–13.

Du, G. and Wang, D. (2003). Tetrahedral mesh generation

and optimization based on centroidal voronoi tessella-

tions. Inter. Journal on Numerical Methods in Engi-

neering, 56(9):1355–1373.

George, P. L. and Borouchaki, H. (1998). Delaunay Tri-

angulation and Meshing: Application to Finite Ele-

ments. Editions HERMES, Paris, France.

Gevers, T. (2002). Adaptive image segmentation by com-

bining photometric invariant region and edge informa-

tion. In IEEE Trans. on Pattern Analysis and Machine

Intelligence, volume 24.

Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:

A high resolution 3d surface construction algorithm.

In SIGGRAPH’87, volume 21, Anaheim. Computer

Graphics.

Owen, S. (1998). A survey of unstructured mesh genera-

tion technology. In Proceedings of the Seventh Inter-

national Meshing Roundtable, Dearborn, Michigan.

Sandia National Laboratories.

Shewchuk, J. R. (2002). Delaunay reﬁnement algorithms

for triangular mesh generation. Computational Ge-

ometry: Theory and Applications, 22:21–74.

Smith, S. M. and Brady, J. M. (1996). Susan - a new ap-

proach to low level image processing. Inter. Journal

of Computer Vision.

Spanel, M., Krsek, P., Svub, M., Stancl, V., and Siler, O.

(2007). Delaunay-based vector segmentation of vol-

umetric medical images. In In Proc. of CAIP 2007,

pages 261–269. LNCS 4673.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

138