VISUALIZATION BY EXAMPLE

A Constructive Visual Component-based Interface for Direct Volume Rendering

Bingchen Liu, Burkhard W¨unsche and Timo Ropinski

University of Auckland, Private Bag 92019, Auckland, New Zealand

University of M¨unster, M¨unster, Germany

Keywords:

Direct volume rendering, Transfer functions, Visual interfaces, Visualizations, Histograms.

Abstract:

The effectiveness of direct volume rendered images depends on ﬁnding transfer functions which emphasize

structures in the underlying data. In order to support this process, we present a spreadsheet-like construc-

tive visual component-based interface, which also allows novice users to efﬁciently ﬁnd meaningful transfer

functions. The interface uses a programming-by-example style approach and exploits the domain knowledge

of the user without requiring visualization knowledge. Therefore, our application automatically analysis his-

tograms with the Douglas-Peucker algorithm in order to identify potential structures in the data set. Sample

visualizations of the resulting structures are presented to the user who can reﬁne and combine them to more

complex visualizations. Preliminary tests conﬁrm that the interface is easy to use, and enables non-expert

users to identify structures which they could not reveal with traditional transfer function editors.

1 INTRODUCTION

Direct Volume Rendering (DVR) is a popular tech-

nique for exploring and visualizing 3D data sets

directly without requiring intermediate representa-

tions. Traditional DVR is described by the emission-

absorption model, where scalar values are interpreted

as densities of a gaseous material which emits and

absorbs light. An image is created by accumulating

the total light intensity for each pixel of a view plane.

This computation requires the deﬁnition of transfer

functions which associate intensities in the volume

with optical properties, i.e., color and opacity.

The main challenge in DVR is to ﬁnd transfer

functions which reveal structure in the data, differen-

tiate materials and reveal relationships between dif-

ferent structures. This requires an appropriate choice

of colors, opacities and boundaries between differ-

ent materials which requires careful selection of the

shape, extend and value of the color and opacity trans-

fer functions. This task is especially challenging for

users without visualization experience. Our prelimi-

nary tests with four inexperienced users revealed that

none of them was able to create meaningful visualiza-

tions for medical imaging data sets without a detailed

explanation of a traditional transfer function design

interface. Furthermore, the users required a detailed

explanation of what to look for and how these struc-

tures are represented in the data set’s histogram. In or-

der to make DVR available to a wider range of users a

more intuitive and easy-to-use interface for exploring

data sets must be found.

In this paper we present a novel spreadsheet-style

interface which allows inexperienced users to uti-

lize DVR applications without having to study the

complex underlying mathematical and optical mod-

els. Section 2 reviews existing interfaces for transfer

function design. Sections 3 and 4 present the design

and implementation details of our interface. Visual-

ization results and the ﬁndings of a preliminary user

study with our new interface are discussed in Sec-

tion 5. Section 6 concludes the paper and discusses

future work.

2 LITERATURE REVIEW

Existing tools for transfer function design can be dif-

ferentiated into image- and data-driven algorithms

and combinations of them (Yoo et al., 2002). Initial

research in transfer function design utilized a data-

driven approach, i.e., the transfer functions resulted

254

Liu B., Wuensche B. and Ropinski T. (2010).

VISUALIZATION BY EXAMPLE - A Constructive Visual Component-based Interface for Direct Volume Rendering.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 254-259

DOI: 10.5220/0002844102540259

 SciTePress

from an analysis of the underlying data set. Kindl-

mann and Durkin use the data values, ﬁrst derivatives

and second derivatives to construct a 3D histogram in

which they detect boundary features (Kindlmann and

Durkin, 1998). Sato et al. improve material differ-

entiation by characterizing local structures into line-

like, sheet-like, and blob-like features (Sato et al.,

2000). Kindlmann et al. present curvature-based

transfer functions using a convolution-based deriva-

tive measurement scheme (Kindlmann et al., 2003).

Caban et al. search for texture patterns in the data set

in order to differentiate materials (Caban and Rhein-

gans, 2008). Due to the lack of intuitive relationship

with the resulting visualization, data-driven methods

can be considered as less suitable for interactive ap-

proaches – especially for inexperienced users.

In contrast image-driven transfer function design

methods enable users to interact directly with the vi-

sualization. An early example (He et al., 1996) uses

randomly generated or predeﬁned transfer functions.

The resulting DVR images are presented to the user

as a table and are iteratively used to create new trans-

fer functions. Jankun-Kelly and Ma (Jankun-Kelly

and Ma, 2001) use a spreadsheet-like interface, which

captures all parameters modiﬁcations and intermedi-

ate visualization results. This allows the user to mod-

ify parameters of the transfer functions and DVR al-

gorithm based on desirable previous visualization re-

sults. In order to get more control about the visu-

alization results a higher-dimensional transfer func-

tion can be used. Tzeng et al. have chosen this way

and provide a sketch interface which enables users

to indicate regions of high and low interest in image

slices (Tzeng et al., 2003). A similar but more direct

approach is used by Ropinski et al. (Ropinski et al.,

2008). The user selects a feature of interest by draw-

ing strokes directly onto the volume rendering near

its silhouette. The information is used to identify the

feature in the histogram space and generate an appro-

priate component transfer function.

A promising approach is to combine the advan-

tages of both data- and image-driven approaches.

Kniss et al. achieve this by allowing the user to place

data probes into the visualization to capture regions

of interest (Kniss et al., 2002). The underlying data

is then highlighted in a multi-dimensional histogram

(e.g., data values and ﬁrst derivatives) and multi-

dimensional transfer functions can be constructed us-

ing interactive widgets in order to capture these fea-

tures. While the interface is intuitive and ﬂexible the

last step requires some knowledge of visualizations

and DVR.

3 DESIGN

The goal of our research is to create a DVR inter-

face for users without any experience in visualization

and DVR. Our only assumption is that the user has

some knowledge of the application domain. Since

the human brain has highly evolved pattern recog-

nition and 3D perception abilities we propose a vi-

sual “programming-by-example” approach: the user

is presented basic visualizations of the data set and

has to assemble more complex ones by interacting

with the images. This requires solutions to the fol-

lowing three problems. Automatically create basic vi-

sualizations which provide a good basis for exploring

the data set and creating complex meaningful visual-

izations. Present the visualizations in a way which

enables the user to assess and select desirable visual-

izations. Provide an interface which allows the user

to combine, reﬁne and modify existing visualizations.

3.1 Unit Transfer Functions

As seen in Section 2, designing a complex meaning-

ful transfer function is difﬁcult. A possible solution to

that problem is to create simple visualizations which

the user recognizes or at least can comprehend and

to “assemble” them to more complex ones using the

user’s application domain knowledge. To generate

such simple visualizations we introduce “unit trans-

fer functions”, which visualize only one structure in

the data set. In order to provide a good basis for ex-

ploration, the unit transfer function must cover a wide

variety of structures (different material properties).

Previous research has demonstrated that structures

in a scalar volume data set can often be characterized

by the ﬁrst and second order derivatives (Kindlmann

and Durkin, 1998). A region is classiﬁed as bound-

ary material, when two materials are relatively thick

and have a thin transition region or if two materials

have very different densities in which case the den-

sities increase/decrease rapidly throughout the transi-

tion region. In either case the materials form a peak

and the transition region a valley in the resulting his-

togram. We can therefore characterize many struc-

tures as peaks in the histogram where the size (num-

ber of voxels) of a peak corresponds to the size of the

corresponding structure(s).

We can hence construct unit transfer function as

follows: We generate a histogram by creating a bin

for each value of the range of density values in the

data set and compute the number of voxels with

that value. Since the difference between maximum

and minimum values of bins often varies dramati-

cally we use the normalized logarithmic values of

VISUALIZATION BY EXAMPLE - A Constructive Visual Component-based Interface for Direct Volume Rendering

255

the original histogram values (we use the function

log(ValueOfTheCurrentBin)/log(MaxValue)). The

histogram is represented by a 2D curve where each

tuple (binValue, #voxelsWithThatValue) is a point.

The key element of our algorithm is to simplify this

curve and identify its main peaks (key features of the

original histogram). We achieve this by using the

Douglas-Peucker algorithm (Peucker, 1973), which

works as follows. Specify an ε value for the maxi-

mum allowed error of the approximated curve. In our

case this value corresponds to the size of features we

capture. For ε = 0 we get the original smoothed his-

togram and for ε = maximumBinValue we get only

one peak corresponding to the peak of the histogram.

Afterwards a polyline S is created, which initially

only contains the ﬁrst and last point of the curve (left

and right most value in the histogram). Then the dis-

tances of all points to the line are computed. If the

maximum distance is smaller than ε then stop. Other-

wise add the point P which is of maximum distance to

the line to S and call the algorithm recursively for the

two sections of the curve on either side of P. Figure 1

demonstrates the effect of applying this algorithm.

Figure 1: The red line represents the original histogram of

the nucleon data set in Figure 4 and the black line represents

the result of applying the Douglas-Peucker algorithm with

ε = 10 to the histogram. Note that the second curve is scaled

in y-direction to improve readability.

We sort the peaks in the resulting histogram by im-

portance (currently determined by their height relative

to the valleys on either side) and deﬁne for each peak

a unit transfer function capturing only the region rep-

resented by that section of the histogram. Each unit

transfer function is associated with one random color

value and an opacity value which increases linearly

with the density value of the corresponding peak in

the histogram. Note that this decision makes the as-

sumption that the region with the highest density are

inside the data set and regions with lower density out-

side. This is the case for many physical and medical

data sets, e.g., computed tomography (CT) where the

density of bone is higher than the density of muscle

which in turn is higher than that of fat and skin.

3.2 Spreadsheet-Like Interface

In order to achieve a “programming-by-example” ap-

proach, we use two spreadsheet-like tables to display

the current and previous visualization results. The

ﬁrst row contains initially the automatically generated

unit transfer functions. The user can select meaning-

ful images and add them to the second row containing

previous visualizations. One or multiple visualiza-

tions in of this section can then be selected and mod-

iﬁed, combined or reﬁned – the results are displayed

in the top row. The bottom section of the interface

contains the buttons for the operations for modifying

visualizations (by modifying the underlying transfer

functions). Figure 2 demonstrates the interface. The

histogram in the bottom-left is for illustrativeand test-

ing purposes and is not shown to inexperienced users.

Figure 2: The spreadsheet-like interface deﬁning complex

transfer functions.

3.3 Operations on Unit Transfer

Functions

The user can “assemble” complex transfer functions

out of the selected unit transfer functions by using the

following operations:

The “search around a feature” function is applied

to one visualization selected by the user. It ﬁnds the

peaks in the histogram surrounding the peak corre-

sponding to the transfer function of the current visu-

alization and creates unit transfer functions for them.

Note that in contrast to the initial selection of peaks

this approach selects any peak regardless of the size

and the height of the peak.

The “interpolation” function is applied to two vi-

sualizations selected by the user. It examines the sec-

tion of the histogram between the peaks of the cor-

responding transfer functions and then ﬁnds the three

largest peaks within it or, if there are no peaks, places

the transfer functions equidistantly in between. This

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

256

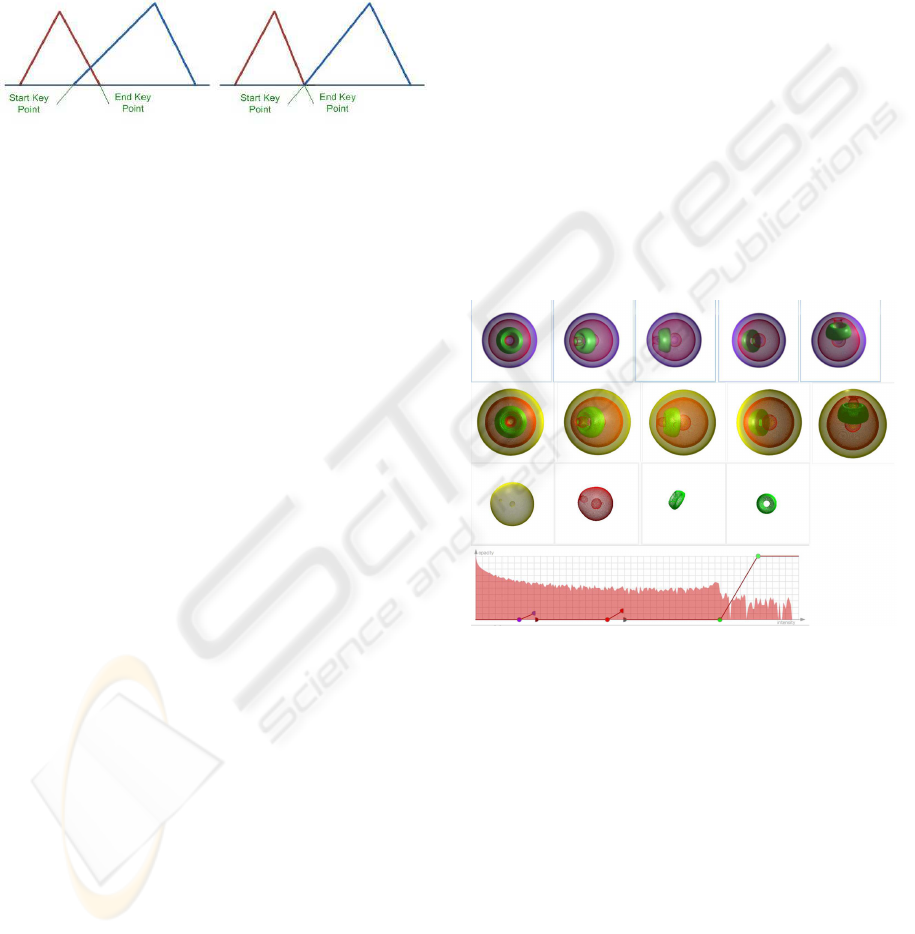
is achieved by using the Douglas-Peuker algorithm

with decreasing ε values until three peaks are found

or until ε = 2.

The “merge” function combines selected visual-

izations. Currently it can only be applied to unit

transfer functions and is achieved by combining them

and removing any overlapping sections as indicated

in Figure 3.

Figure 3: Merging of two overlapping transfer functions

(left) and the results after removing the overlapping section

(right).

4 IMPLEMENTATION

Our implementation is based on Voreen (Meyer-

Spradow et al., 2009), a rapid-prototyping environ-

ment for ray-casting-based volume visualizations.

Voreen uses GPU-acceleration for rendering, which is

abstracted through an object-oriented structure, which

represents each phase of the DVR process as individ-

ual processors. Since Voreen is developed with C++

and the Qt UI framework, we develop our interface

with Qt and integrate Voreen using a

QWidget

. We

set up all rendering steps of the DVR process by deﬁn-

ing a standard DVR network. Each transfer function

is stored as a

TransFuncIntensity

object and asso-

ciated with a

VoreenPainter

object and connected

with a

QtCanvas

representing a cell in the spread-

sheet.

5 RESULTS

We have evaluated our tool by using real and simu-

lated data sets from different application ﬁelds.

5.1 Visualization Results

For the NCAT phantom dataset (8 Bit, 128

voxels)

shown in Figure 2, we asked a computer science stu-

dent without any experience in medical imaging to

generate a transfer function with our technique. Cre-

ating the visualization took this inexperienced user

less than 30 seconds and was achieved by simply

combining the visualizations corresponding to the au-

tomatically created unit transfer functions. In con-

trast, an experienced user required about 90 seconds

for generating a comparable transfer function with the

original Voreen interface. Besides the used colors,

which are so far randomly assigned in our approach,

the results where almost identical.

The example shown in Figure 4, is a simulation of

the two-body distribution probability of a nucleon in

the atomic nucleus (8Bit, 41

voxels) obtained from

www.volvis.org

. We asked an inexperienced stu-

dent to create a meaningfulvisualization with both the

traditional transfer function design interface within

Voreen (Meyer-Spradow et al., 2009) and our inter-

face. The ﬁrst row of Figure 4 shows the visualization

rendered with Voreen, where the transfer functions

has been manually deﬁned by the user. The second

row shows the visualization obtained with our inter-

face. The third row shows the unit functions used to

generate the visualization in row one. The fourth row

shows the transfer function generating the visualiza-

tions in row two. This transfer function has been gen-

erated with Voreen’s standard transfer function editor.

Figure 4: Nucleon dataset DVR visualization. It includes

the visualization generated directly with Voreen in the ﬁrst

row, the visualization generated with our interface in the

second row, the unit function used in our interface in the

third row, and the transfer function used in the visualization

of Voreen in the last row.

It can be seen that the manually deﬁned trans-

fer functions result in sharper “material boundaries”

and more appropriate opacity values which makes

shape perception slightly easier. The reason for this

is that our unit transfer functions always have a tri-

angle shape and the user can not modify opacity

values. Note that the two visualizations seem to

show different “material boundaries”. Both solutions

are correct, however, since the nucleus data set has

smoothly varying values and hence the perceived ma-

terial boundaries are purely illustrative. The surfaces

VISUALIZATION BY EXAMPLE - A Constructive Visual Component-based Interface for Direct Volume Rendering

257

give an indication of the density value change, but

they do not indicate different “materials”. Overall,

the user in our test found it considerable easier to cre-

ate the visualization with our interface and required

much less time.

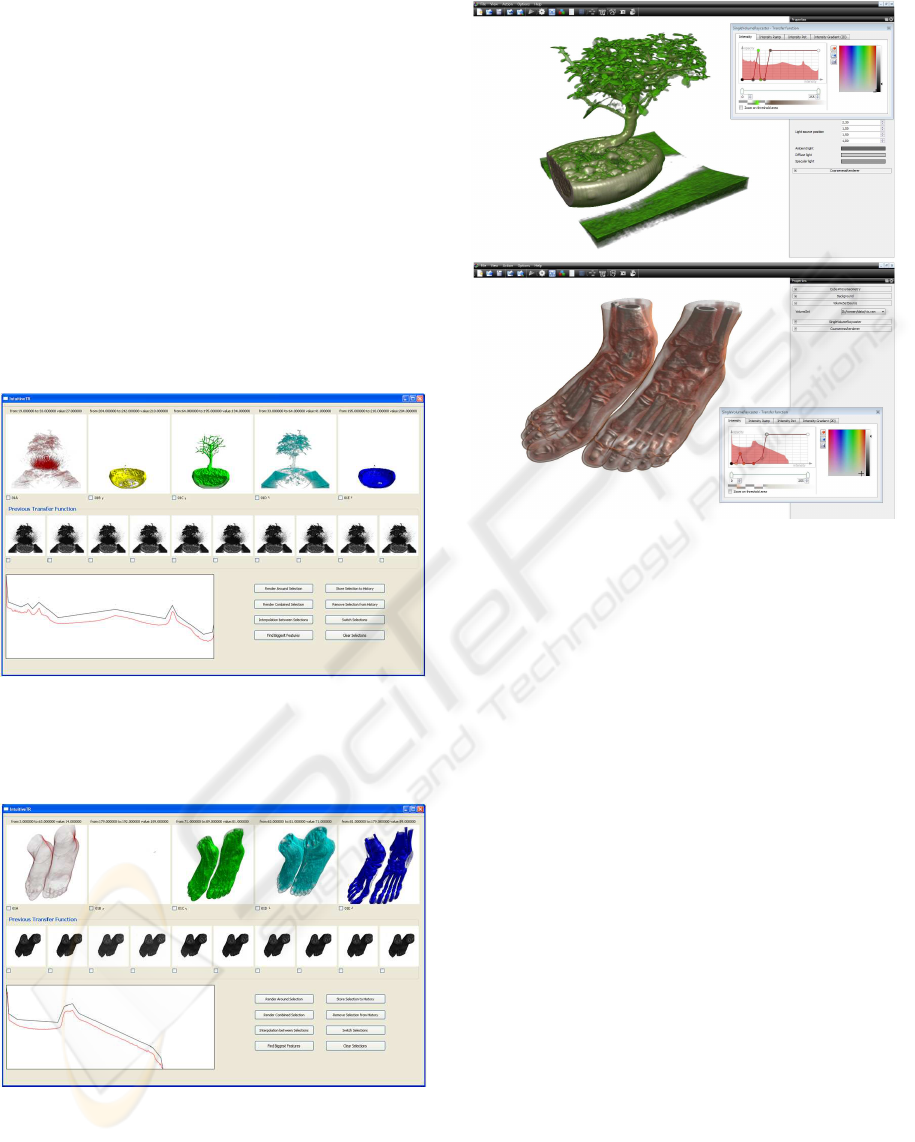
Figures 5 and 6 show two further examples us-

ing real world data sets. Note that in both examples

our interface results in meaningfulvisualizations. Our

method has limitations, though, as is illustrated by

the expert visualizations in ﬁgure 7. It can be clearly

seen that the visualization of the two feet CT using the

traditional Voreen interface shows considerable more

structures. The main reasons for this are that some tis-

sue structures do not correspond to histogram peaks,

but also that tissue boundaries have been enhanced

using shading functions.

Figure 5: Visualization of a Bonsai CT data set (8Bit, 256

voxels) with our spreadsheet-like interface. The bottom left

graph shows the original histogram (red) and its main peaks

identiﬁed with the Douglas-Peucker algorithm (black).

Figure 6: Visualization of CT scan of two feet (16Bit,

256× 256× 250 voxels) provided by Osirix and visualized

using our spreadsheet-like interface. The bottom left graph

shows the original histogram (red) and its main peaks iden-

tiﬁed with the Douglas-Peucker algorithm (black).

Figure 7: Expert results for the data sets in ﬁgure 5 and 6

obtained using the traditional Voreen transfer function in-

terface.

5.2 Usability

Our preliminary users tests suggest that meaningful

visualizations can be constructed with our interface

in less than a minute. Several users struggled with

the nucleus data set in ﬁgure 4 because they did not

know what it represents. None of the users was able

to create high quality visualization of the CT feet

data set because of the lack of relationship of data

set features and histogram features. Users were also

confused about the lack of spatial relationships when

modifying visualizations. In particular they expected

that reﬁning a visualization would result in structures

close to the currently visualized structure. This is of-

ten not the case since neighboring peaks in the his-

togram can correspond to spatially completely unre-

lated structures.

5.3 Discussion

Compared with a traditional transfer function design

tool our approach is faster and required no knowl-

edge of the DVR process and transfer functions. In

all cases we investigated our tool was able to cre-

ate meaningful visualizations. Since the user does

not have any direct control about the transfer func-

tions the resulting visualizations can be less accurate

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

258

than when using a traditional transfer function design

tool. Our examples show that there are three imple-

mentation issues which must be resolved: The lack

of color control can result in ambiguities if two dif-

ferent materials have very similar colors. The use

of increasing opacity values for the peaks of the vol-

ume’s histogram works well for objects where the in-

nermost structures have the highest densities, e.g., CT

data sets, but is not a suitable solution for general ap-

plications. Finally the use of a one-dimensional his-

togram and the restrictions to identifying peaks in the

histogram can be insufﬁcient for identifying all struc-

tures in a data set.

6 CONCLUSIONS AND FUTURE

WORK

The usage of DVR in science, engineering and other

application areas can be signiﬁcantly expanded by

providing users with a simple and intuitive tool for

representing structure in the data. We have de-

signed such a tool by combining a “programming-by-

example” approach with an automatic transfer func-

tion design technique. In contrast to previous publica-

tion our transfer functions are deﬁned as combination

of so-called unit transfer function. Each unit transfer

function captures one structure in the data set by rep-

resenting one feature in the data set’s histogram. Fea-

tures are identiﬁed by applying the Douglas-Peucker

algorithm to the histogram curve. By choosing dif-

ferent epsilon values for the Douglas-Peucker algo-

rithm features with different variations can be differ-

entiated, which in many cases will correspond to an

order by importance. Using a wide variety of data sets

we have demonstrated, that complex visualization can

be constructed without requiring knowledge regard-

ing the DVR algorithm, transfer functions or image

histograms.

We have only just started to explore the possibil-

ities offered with our new concept. Future research

will concentrate on improved unit transfer functions

as well as improved user interaction. Furthermore,

we are interested in extending the technique to multi-

dimensional transfer functions (Kniss et al., 2002).

We also believe, that the usability of the tool can be

improvedby determining an optimal layout of the ren-

dering results of unit transfer functions and interme-

diate visualization results, and by supporting the com-

bination via drag-and-drop. Interaction with transfer

functions can be improved by adding sketch-based in-

terfaces as presented in (Ropinski et al., 2008).

REFERENCES

Caban, J. J. and Rheingans, P. (2008). Texture-based

transfer functions for direct volume rendering. IEEE

Transactions on Visualization and Computer Graph-

ics, 14(6):1364–1371.

He, T., Hong, L., Kaufman, A., and Pﬁster, H. (1996).

Generation of transfer functions with stochastic search

techniques. In VIS ’96: Proceedings of the 7th confer-

ence on Visualization ’96, pages 227–ff.

Jankun-Kelly, T. J. and Ma, K.-L. (2001). Visualization ex-

ploration and encapsulation via a spreadsheet-like in-

terface. IEEE Transactions on Visualization and Com-

puter Graphics, 7(3):275–287.

Kindlmann, G. and Durkin, J. W. (1998). Semi-automatic

generation of transfer functions for direct volume ren-

dering. In VVS ’98: Proceedings of the 1998 IEEE

symposium on Volume visualization, pages 79–86.

Kindlmann, G., Whitaker, R., Tasdizen, T., and Moller, T.

(2003). Curvature-based transfer functions for direct

volume rendering: Methods and applications. In VIS

’03: Proceedings of the 14th IEEE Visualization 2003

(VIS’03), page 67.

Kniss, J., Kindlmann, G., and Hansen, C. (2002). Multi-

dimensional transfer functions for interactive volume

rendering. IEEE Transactions on Visualization and

Computer Graphics, 8(3):270–285.

Meyer-Spradow, J., Ropinski, T., Mensmann, J., and Hin-

richs, K. (2009). Voreen: A rapid-prototyping envi-

ronment for ray-casting-based volume visualizations.

IEEE Computer Graphics and Applications, 29(6):6–

13.

Peucker, D. D. . T. (1973). Algorithms for the reduction of

the number of points required to represent a digitized

line or its caricature. The Canadian Cartographer,

10(2):112–122.

Ropinski, T., Praßni, J.-S., Steinicke, F., and Hinrichs, K. H.

(2008). Stroke-based transfer function design. In

IEEE/EG Volume and Point-Based Graphics, pages

41–48.

Sato, Y., Westin, C.-F., Bhalerao, A., Nakajima, S., Shiraga,

N., Tamura, S., and Kikinis, R. (2000). Tissue classi-

ﬁcation based on 3d local intensity structures for vol-

ume rendering. IEEE Transactions on Visualization

and Computer Graphics, 6(2):160–180.

Tzeng, F.-Y., Lum, E. B., and Ma, K.-L. (2003). A novel

interface for higher-dimensional classiﬁcation of vol-

ume data. In Proceedings of the 14th IEEE Visualiza-

tion 2003 (VIS’03), page 66.

Yoo, T., Gerig, G., Whitaker, R., Kindlmann, G., Machiraju,

R., and M¨oller, T. (2002). Image processing for vol-

ume graphics. Course notes #50, ACM SIGGRAPH

2002.

VISUALIZATION BY EXAMPLE - A Constructive Visual Component-based Interface for Direct Volume Rendering

259