MRI

IMAGE ENHANCEMENT

A PDE-based Approach Integrating a Double-well Potential Function for Thin

Structure Preservation

A. Histace

ETIS UMR CNRS 8051, ENSEA-UCP, 6 avenue du Ponceau, 95014 Cergy, France

M. M

enard

L3i, University of La Rochelle, Pole Sciences et Technologie, 17000 La Rochelle, France

Keywords:

Image diffusion, Double well potential, Directional diffusion, Selectivity.

Abstract:

Non-linear or anisotropic regularization PDE’s (Partial Differential Equation) raised a strong interest in the

ﬁeld of medical image processing. The beneﬁt of PDE-based regularization methods lies in the ability to

smooth data in a nonlinear way, allowing the preservation of important image features (contours, corners or

other discontinuities). In this article, we propose a PDE-based method restoration approach integrating a

double-well potential as diffusive function. It is shown that this particular potential leads to a particular regu-

larization PDE which makes the integration of prior knowledge about the gradient intensity level to enhance

possible. The corresponding method shows interesting properties regarding stability and preservation of ﬁne

structures. As a proof a feasibility, results of restoration are presented on natural images to show potentialities

of the proposed method. We also address a particular medical application: enhancement of tagged cardiac

MRI.

1 INTRODUCTION

In the particular ﬁeld of image restoration, non-

linear or anisotropic regularization PDE’s are of pri-

mary interest. The beneﬁt of PDE-based regular-

ization methods lies in their ability to smooth data

in a nonlinear way, allowing the preservation of im-

portant image features (contours, corners or other

discontinuities). In the particular domain of scalar

image restoration, a lot of studies have been pre-

sented in the literature so far: (Perona and Malik,

1990), (Alvarez et al., 1992), (Catt

e et al., 1992),

(Geman and Reynolds, 1992), (Nitzberg and Sh-

iota, 1992), (Whitaker and Pizer, 1993), (Weick-

ert, 1995), (Deriche and Faugeras, 1996), (Weickert,

1998), (Terebes et al., 2002), (Tshumperl

e and De-

riche, 2002), (Tschumperle and Deriche, 2005) for the

main references.

In the particular ﬁeld of medical image process-

ing, PDE based approach for denoising are very

promising tools, but generally needs to be adapted to

the imaging context (PET, CT, Cone-beam CT, MRI,

etc.) since noise can be of very different types (Gaus-

sian, Poisson, Rayleigh). In (Histace et al., 2009), we

showed that, considering a particular general param-

eterizable PDE, it was possible to integrate selectiv-

ity regarding the gradient directions to diffuse or not

within the considered image. Qualitative and quanti-

tative results were also presented on a particular med-

ical application: enhancement of tagged cardiac MRI.

In this article, we propose a complementary PDE

to the one presented in (Histace et al., 2009) which en-

ables integration of selectivity regarding the intensity

of the gradient to restore and which makes the preser-

vation of thin structures from the diffusive effect pos-

sible. More precisely, we propose to make this selec-

tivity possible thanks to the integration of a double-

well potential diffusion function within the classical

Perona-Malik’s PDE (Perona and Malik, 1990). That

kind of approaches can be of interesting beneﬁts for

medical image restoration and particularly for MRI

enhancement, since even thin structures can be of pri-

mary importance to establish the most appropriate di-

agnosis.

Our aims and motivation for such a study are

mainly to show that, ﬁrstly, such a choice can lead to

501

Histace A. and Ménard M. (2010).

MRI IMAGE ENHANCEMENT - A PDE-based Approach Integrating a Double-well Potential Function for Thin Structure Preservation.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 501-508

DOI: 10.5220/0002887605010508

 SciTePress

a stable PDE-based approach for scalar image denois-

ing that can overpass classical approach of Perona-

Malik’s from which it is derived and which presents

instability problems as formerly shown in (Catt

e et al.,

1992). Secondly, we also want to show that this inte-

gration leads to a selective PDE-based approach that

overcomes classical mean curvature or tensor driven

diffusion problems, which in the particular case of di-

rectional diffusion are not suitable (see (Histace et al.,

2005) and (Terebes et al., 2002)) because they tend to

smooth transitions between patterns.

Regarding the medical application we want to ad-

dress in this article, we propose to tackle a known

problem of us: enhancement of tagged cardiac MRI.

Such a choice is guided by the fact that we have

already worked on that particular MR imaging se-

quence and that qualitative results have already been

computed for comparison. Moreover, as said in sec-

tion 3, this particular sequence of acquisition can be

of primary importance for the follow-up of cardiovas-

cular pathologies and totally ﬁt the problem we want

to address: preservation of thin structures within the

enhanced data.

This article is organized as follows: In a section

two, we propose some recalls about PDE-based reg-

ularization approaches. Section three deals with the

general presentation of the tagged cardiac MR im-

ages problematic. Fourth section is dedicated to the

study of the double well function and of its mathe-

matical properties. Prospective results on “lena” are

also shown in this section. Section ﬁve deals with

the enhancement of tagged MRI: Comparative results

are shown and commented. Finally, the proposed ap-

proach and the obtained results are discussed in last

section.

2 PDE BASED

REGULARIZATION

APPROACH: A GENERAL

SCHEME

In (Deriche and Faugeras, 1996), authors propose a

global scheme for PDE-based restoration approaches.

More precisely, if we denote ψ(r,t) : R

× R

→

R the time intensity function of a corrupted image

= ψ(r,0), the corresponding regularization prob-

lem of ψ

is equivalent to the minimization problem

described by the following PDE:

∂ψ

∂t

= c

(k∇ψk)

∂

∂ξ

+ c

(k∇ψk)

∂

∂η

, (1)

where η = ∇ψ/k∇ψk, ξ⊥η and c

and c

are two

weighting functions (also called diffusive functions).

This PDE can be interpreted as the superposition

of two monodimensional heat equations, respectively

oriented in the orthogonal direction of the gradient

and in the tangential direction: It is characterized by

an anisotropic diffusive effect in the privileged direc-

tions ξ and η allowing a non-linear denoising of scalar

image.

Eq. (1) is of primary importance, for all classical

methods can be expressed in that global scheme: For

instance, if we consider the former anisotropic diffu-

sive equation of Perona-Malik’s (Perona and Malik,

1990) given by

∂ψ

∂t

= div(c(k∇ψk)∇ψ) , (2)

with ψ(r,0) = ψ

and c(.) a monotonic decreasing

function, it is possible to express it in the global

scheme of Eq. (1) with

(

= c(k∇ψk)

= c

(k∇ψk).|∇ψ| + c(k∇ψk)

(3)

Formulation of Eq. (1) is also interesting, for it makes

stability study of classical proposed methods possible.

More precisely, a stable PDE-based method for de-

noising will be characterized by a weighting function

positive for all values of k∇ψk as formerly shown

in (Catt

e et al., 1992). In practice, c

(.) function has

also to be of small values in order to diffuse the data in

the tangential direction of the image boundaries only.

This last property is of primary importance for the

preservation of thin structures since only a “small”

diffusive effect in the orthogonal direction of the cor-

responding gradient can lead to a low alteration of

them.

What we proposed in this article is a study for the

integration of a double well potential as a diffusive

function c(.) in Eq. (2).

3 TAGGED CARDIAC MRI

Mainly, to help cardiologists to establish a pre surgery

scheme for reperfusion of myocardial tissue after an

infarction, a study of the myocardial local viability is

necessary: Whereas classical cardiac MRI does not

make the study of the local contraction of the my-

ocardium possible, tagged cardiac MRI allows this lo-

cal estimation. More precisely, the classical SPAMM

(Space Modulation of Magnetization) acquisition pro-

tocol (Zerhouni et al., 1988) used for the tagging of

MRI data, displays a deformable 45-degrees oriented

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

502

dark grid which describes the contraction of my-

ocardium (Fig. 1) on the images of temporal Short-

Axis (SA) sequences. This is the temporal tracking

of this grid that can enable radiologists to evaluate the

local intramyocardial displacements.

Figure 1: SA tagged MRI of the Left Ventricle (LV) ex-

tracted from a sequence acquired between end-diastole and

end-systole.

Tagged cardiac images present peculiar character-

istics which make the analysis difﬁcult. More pre-

cisely, images are of low contrast compared with clas-

sical MRI, the level of corrupting noise is more im-

portant than with classical acquisition and their reso-

lution is only of approximately one centimeter. Nu-

merous studies were carried out concerning the anal-

ysis of the deformations of the grid of tag on SA se-

quences (see (Petitjean et al., 2005; Axel et al., 2007)

for a complete overview) but all have in common

the necessary enhancement of tagged cardiac images

which can be considered as thin oriented structures

since they are only three or four pixels wide.

Classically, in such a framework (oriented pat-

tern enhancement), the classical Edge Enhancing Dif-

fusion (EED) (Weickert, 1995) normally leads to

very satisfying results of regularization. However, as

shown in Fig. 10.(c), the poor quality of tagged car-

diac images makes the computation of the local struc-

ture tensor difﬁcult and, as said in the introduction of

this article, that kind of approaches tends to always

smooth in the orthogonal direction of the image con-

tours: thin stucture are then altered.

As a consequence, diffusive restoration ap-

proaches like the Perona-Malik’s former one (Perona

and Malik, 1990) are more adapted to our purpose: A

non-linear smoothing of the data is performed by tak-

ing into consideration the local value of the gradient

intensity. If this value is small then the corresponding

data are diffused along the tangential direction of the

contour. On the contrary, if this value is important the

diffusive effect is stopped. That kind of approaches

makes the enhancement of the boundaries of the im-

age possible. Nevertheless, as one can notice on Fig.

2, due to the fact that norms of the gradient levels of

tagged MRI are very noisy, it is necessary to develop a

method that integrates within diffusion process more

than only this classical parameter: for instance, cal-

culation and integration of the direction of local gra-

dients of the grid could be of primary interest.

This can be achieved by considering some varia-

tions of the classical restoration approaches. We pro-

pose for example to consider a variant of the Perona-

Malik’s process (Perona and Malik, 1990) given by

∂ψ

∂t

= div(c(||A.∇ψ||)∇ψ) . (4)

with c(u) = e

−

(as proposed by Perona and Malik)

and A is a vector ﬁeld deﬁning the particular direc-

tion(s) to preserve from the diffusion process (in this

particular medical application, the gradient direction

of the grid). k represents here a soft threshold driv-

ing the decrease of c(.). In both cases, the directional

weighting of the diffusion process is driven by the

scalar product between the norm of the local gradient

and A. As a consequence when local gradient and A

are parallel, there is no diffusion, for c(||A.∇ψ||) = 0,

whereas all other directions are diffused: the grid of

tags is normally enhanced.

(a) (b)

Figure 2: (a) Original Image, (b) Norm of the corresponding

gradients.

Nevertheless, because of instability problems (see

section 4 for more details) of PM’s approach, it ap-

pears that process of Eq. (4) does not lead to inter-

esting results (see Fig. 10.(b)). Such a problem can

be overcome by a Gaussian ﬁltering of the gradient

data as proposed in (Catt

e et al., 1992). But, such

a Gaussian ﬁltering will also have for consequences

an increase of the values corresponding to the diffu-

sive effect in the orthogonal direction of the contours.

As explained before, the corresponding approach will

then not make preservation of thin structures possible.

Moreover, the classical c(.) function does not

allow to integrate within the iterative restoration

scheme selectivity regarding the preservation of par-

ticular gradient levels. However, such a selectivity

would be of signiﬁcant beneﬁts since value of the

tags’ gradient can be easily identiﬁed (Denney, 1999).

To overpass the drawbacks of Eq. (4) , we propose

to dethin c(.) as a double well potential function. This

particular function will make integration of gradient

level selectivity possible as well as the obtaining of a

stable PDE and the preservation of thin structures.

MRI IMAGE ENHANCEMENT - A PDE-based Approach Integrating a Double-well Potential Function for Thin Structure

Preservation

503

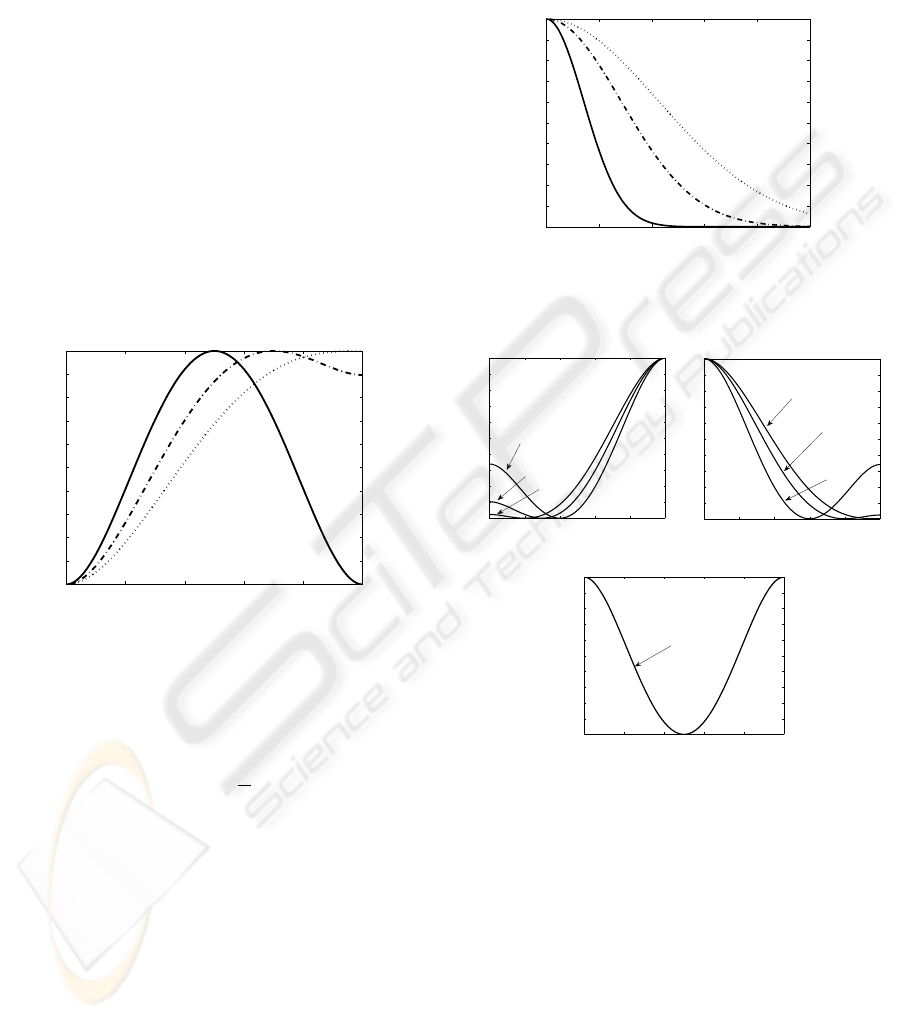
4 DOUBLE WELL POTENTIAL

AND CORRESPONDING PDE

4.1 Diffusive Function

The double well potential considered in this article is

dethind by the following function:

φ(u) =

v(α − v)(v − 1)dv . (5)

Some graphical representations of Eq. (5) for differ-

ent values of α are proposed Fig. 3.(a). The roots

of the corresponding non linear force (i.e. f (u) =

u(α − u)(u − 1)) 0, and 1 corresponds to the local

positions of the minima of the potential, whereas the

root α represents the position of the potential maxi-

mum. The non linearity threshold α dethins the po-

tential barrier between the potential minimum with

the highest energy and the potential maximum.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

φ(u)

Figure 3: Plots of double well potential φ(.) of Eq. (5) for

different values of α ∈ [0.5,1]. Solid lines stand for α = 0.5,

dash-dotted lines for α = 0.7 and dotted lines for α = 1.

This function has to be compared with the classi-

cal Perona-Malik’s function c

(.) given by:

(u) = e

−

, (6)

with k a soft threshold deﬁning selectivity of c

(.)

regarding values of image gradients. Fig. 4 shows

graphical representations of c

(.) dethind by Eq. (6)

for different values of k.

As one can notice on Fig. 4.(a), for k∇ψk →

0, c

(k∇ψk) → 1, whereas for k∇ψk → 1,

(k∇ψk) → 0. As a consequence, boundaries

within images which are on a threshold, function of

k, are preserved from the smoothing effect of Eq. (2).

Regarding Fig. 3, in order to preserve this major prop-

erty with integration of Eq. (5) as a diffusive function

in Eq. (2), it is necessary to dethin this diffusive func-

tion as follows:

(u) = 1 − φ(u) . (7)

Graphical representations of c

are proposed in Fig.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(u)

Figure 4: Plots of function c

(.) of Eq. (6) for different

values of k. Solid lines stand for k = 0.2, dash-dotted lines

for k = 0.4, and dotted lines for k = 0.6.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(u)

α=0.4

α=0.2

α=0.1

(a)

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(u)

α=1

α=0.8

α=0.6

(b)

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(u)

α=0.5

(c)

Figure 5: Plots of function c

(.) of Eq. (5) for different

values of α: (a) 0 < α < 0.5, (b) 0.5 < α < 1, and (c) α =

0.5.

One can notice on Fig. 3 that φ(.) has been nor-

malized. As a consequence, we are able to ensure that

0 ≤ c

(u) ≤ 1 for all values of u like classical PM’s

function of Eq. (2). For 0 ≤ α < 1, since c

is issued

from a double well potential, selectivity of Eq. (2) is

more important and centered on a particular gradient

value function of α. For instance, for α = 0.5, only

gradients of value 0.5 are totally preserved from the

diffusive effect in the tangential direction. This can

be interpreted as an integration of gradient level se-

lectivity within the restoration process.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

504

Moreover, we are now going to show, that inte-

gration of c

as diffusive function leads to interest-

ing stability property of corresponding PDE regarding

properties of the corresponding c

function.

4.2 Study of Stability

It is recognized that classical Perona-Malik’s PDE

presents instability problems. More precisely, as

shown in (Catt

e et al., 1992), sometimes noise can

be enhanced instead of being removed. This can be

explained considering Eq. (3). If we consider c

(.)

function of Eq. (6), it appears that corresponding c

function of Eq. (3), in the global scheme of Eq. (1),

can sometimes takes negative values (see Fig. 6 for

illustrations). This leads to local instabilities of the

Perona-Malik’s PDE which degrades the processed

image instead of denoising it.

0 0.2 0.4 0.6 0.8 1

−0.5

0.5

Figure 6: Plots of function c

for different values of k .

Solid lines stand for k = 0.2, dash-dotted lines for k = 0.4

and dotted lines for k = 0.6.

Now, if we calculate mathematical expression of

with c(.) = c

(.) of Eq. (7), one can obtain that:

(k∇ψk) = c

(k∇ψk).|∇ψ| + c

(k∇ψk) ,

(8)

Taking into account that |∇ψ| ∈ [0..1] and that

(k∇ψk) is a one-order-less polynomial function

than c

(k∇ψk), it happens that:

(k∇ψk) ≈ c

(k∇ψk) = c

(k∇ψk) . (9)

Considering Eq. (9), one can notice that cor-

responding c

function never takes negative values

(see Fig. 5 for illustrations): Diffusive process re-

mains stable for all gradient values of processed im-

age which is of primary importance.

Moreover, we can also notice that c

is exactly

equal to 0 when c

= 0. As a consequence, by a ju-

dicious choice of α, it becomes possible to completely

stop the diffusion process in the tangential and orthog-

onal directions of the contours at the same time. thin

structures characterized by an identiﬁed gradient level

can be preserved from any alterations.

4.3 Experimental Results

We propose in this section to make a visual and quan-

titative comparison between classical Perona-Malik’s

PDE of Eq. (2) with diffusive function c(.) = c

(.)

of Eq. (6), and the following PDE given by:

∂ψ

∂t

= div(c

(k∇ψk)∇ψ) . (10)

For practical numerical implementations, the pro-

cess of Eqs. (2) and (10) are sampled with a time step

τ. The restored images ψ(t

) are calculated at discrete

instant t

= nτ with n the number of iterations.

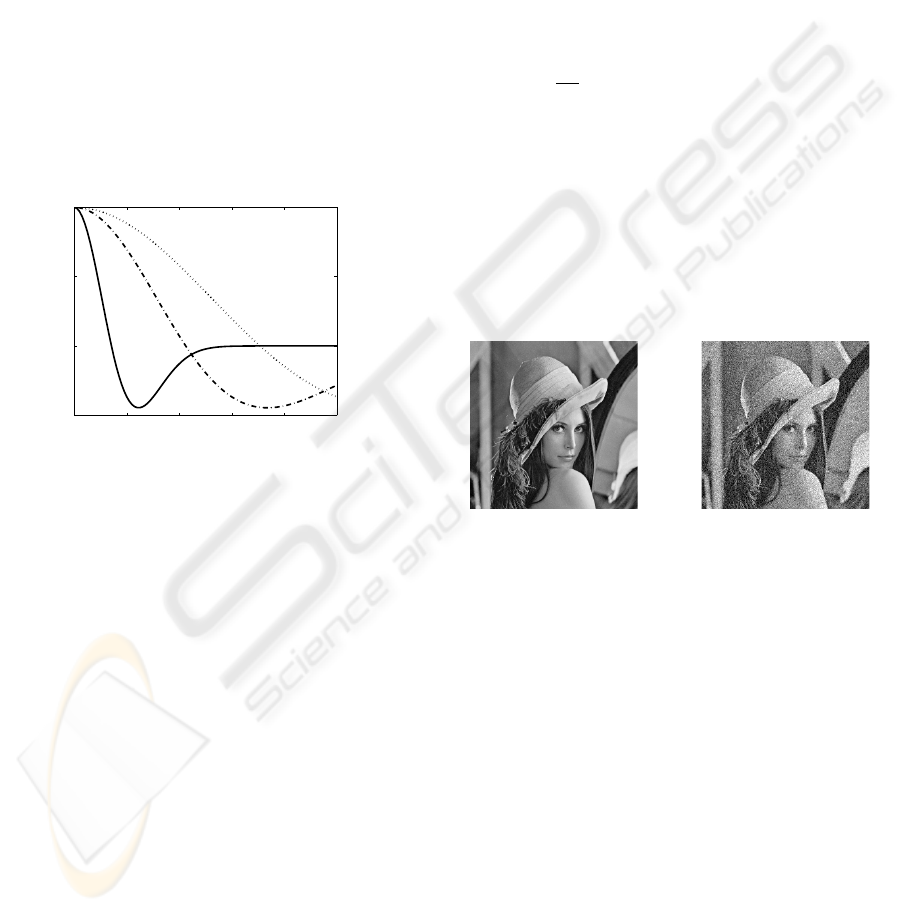
We propose to compare our proposed method with

PM’s approach on the classical “lena” image. For

our purpose, this latter has been corrupted by a white

Gaussian noise of mean zero and standard deviation

σ (see Fig. 7).

(a) (b)

Figure 7: (a) Original image “lena” and (b) its corrupted

version ψ

. Corrupting noise is a white Gaussian one of

mean zero and standard deviation σ = 0.1.

Considering nature of non corrupted image (Fig.

7.(a)), quantiﬁcation of the denoising effect of Eq.

(2) with c(.) = c

(.) and c(.) = c

(.), will be esti-

mated with a classical PSNR measurement.

Once again, because aim of this article is to show

potentiality of the described restoration method, only

optimal results for both compared approaches are pre-

sented Figs. 8 and 9.

One can notice on Figs. 8 and 9 that both visually

and quantitatively, it is possible to ﬁnd a value of α

that can outperform results of optimal classical PM’s

approach. Although the number of iterations corre-

sponding to the optimal restoration results is more im-

portant with the proposed approach of Eq. (10) than

with PM’s approach, quantitatively speaking PSNR is

around 2dB higher, and visually speaking, boundaries

on Fig. 8.(b) are preserved in a better way from the

MRI IMAGE ENHANCEMENT - A PDE-based Approach Integrating a Double-well Potential Function for Thin Structure

Preservation

505

(a)

(b)

Figure 8: (a) Restored image with c(.) = c

(.) (clas-

sical Perona-Malik’s approach), (b) Restored image with

c(.) = c

(.) (proposed approach). The red circles high-

light some regions of interest where the preservation of

edges are better than with Perona-Malik’s approach. k is

equal to 1 for PM’s restoration approach, α is equal to 0.2

for the proposed approach (Eq. (10) (these values have been

empirically tuned). Time step τ = 0.05

0 10 20 30 40 50

138

140

142

144

146

148

150

152

iteration number (n)

PSNR (dB)

Figure 9: PSNR function of iteration number n, solid lines

stands for classical Perona-Malik’s approach, dotted line

stands for the proposed method (Eq. (10). k is equal to 1, α

is equal to 0.2 (these values have been empirically tuned

to obtained the best denoising effects). Time parameter

τ = 0.05 These two curves have been computed by calcula-

tion of the mean results obtained for one hundred different

realizations of the Gaussian corrupting noise.

diffusion effect (see red circles on Fig. 8 for particular

regions of interest).

Nevertheless, this example do not permit to di-

rectly appreciate the possible gradient level selectivity

of the proposed approach. To show it, we are now go-

ing to present some results dedicated to the targeted

medical application : enhancement of tagged cardiac

MRI.

5 TAGGED MRI ENHANCEMENT

We now focus this study on tagged cardiac MRI en-

hancement.

What we propose here is to compare enhancement

results obtained with: (a) the classical PM’s approach,

(b) the classical Weickert’s approach (Weickert, 1995)

(Edge Enhancing Diffusion-EED), (c) with PM’s ap-

proach integrating c

(.) function (Eq. (10), and (d)

with the following PDE:

∂ψ

∂t

= div(c

(||A.∇ψ||)∇ψ) . (11)

function is set in order to entirely preserve the

gradient level of the tag from diffusion. To achieve

this, Fig. 2.(b) is processed so that gradient of the

tags are set to 0.5 and the parameter α is set to the

same value. This choice made for α is based on the

fact that for this particular value, we have shown that

the diffusion process is totally stop in both tangential

and orthogonal direction of the contours, and is the

most selective.

To obtain restoration results with Eq. (11) only

one direction of the grid has been taken into account

thanks a judicious computation of A. More precisely,

each local a priori direction of the corresponding gra-

dient has been estimated thanks to a frequential anal-

ysis of processed image (see (Histace et al., 2009) for

full detailed of the method). In order to compute a

precise estimation of A from the frequential analysis,

we propose to directly use the method of Rao (Rao

and Jain, 1992) and Terebes (Terebes et al., 2002).

As a consequence, each a priori gradient direction

computed from the frequential analysis is preserved

from diffusion effect thanks to A, and c

(.) func-

tion makes the enhancement of the tag possible by

preserving the gradient level of tags from diffusion.

As one can notice, the grid enhancement per-

formed thanks to the classical PM’s approach (Fig.

10.(b)) presents strong instabilities. As a conse-

quence, the resulting enhanced grid is corrupted and

presents no real interest for the tracking of the grid.

Considering now the classical Weickert’s EED (Fig.

10.(c), one can clearly notice that the method fails

in enhancing the tag pattern for the reasons we men-

tioned earlier in the paper. Fig. 10.(d) shows re-

sults obtained with classical PM’s approach but with

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

506

(a)

(c)

(e)

(b)

(d)

Figure 10: Tagged MRI restoration: (a) Original image, (b)

PM’s approach, (c) Weickert’s approach, (d) PM’s approach

with c(.) = c

(.), (e) Result obtained with Eq. (11). “Op-

timal” visual results for each methods are shown.

c(.) = c

(.). The ﬁrst consequence of such a choice

for c(.) function is the absence of stability problems

within the iterative enhancing resulting process. As

one can see, visually speaking the grid is enhanced

and the corresponding boundaries are preserved from

the diffusion effect. Moreover, compare to Weickert’s

EED approach, thin structures (tags mainly) are bet-

ter preserved. If such a result is of real interest, en-

hancement effect can be outperformed by considering

Eq. (11). This time, result shown Fig. 10.(e) clearly

demonstrates the possibility of enhancing the tag pat-

terns by selecting (i) a particular direction, locally

computed thanks to a frequential analysis, and (ii)

a particular gradient-level characterizing the bound-

aries of the tags.

6 DISCUSSION AND

CONCLUSIONS

In this article, we have proposed an alternative diffu-

sive function for restoration of scalar images within

the framework of PDE-based restoration approaches.

The proposed diffusive function allows integrating

prior knowledge on the gradient level to restore thanks

parameter α of Eq. (7) and remains always stable on

the contrary of classical PM’s approach. Proposed

method also remains fast and easy to compute. Visu-

ally and quantitatively speaking, better restoration re-

sults have been obtained, but this point must be now

discussed. Since α parameter ﬁnally corresponds to

integration of prior information about gradient level

to preserve from the diffusion process, it would be

interesting to make an adaptive local use of the pro-

posed approach more than a global use.

If interesting visual and quantitative results have

been obtained on “lena” image thanks to a global

use of the proposed PDE (Eq. (10)), we have also

shown that a judicious tuning of this parameter in

terms of particular localization within the processed

image (Eq. (11) could lead to more interesting results

than classical approaches on a particular medical ap-

plication: enhancement of tagged cardiac MR images.

More precisely, thin structures are less altered by the

proposed diffusive scheme. Strategy for a local tun-

ing of α still to be now completely automatized. For

instance, in the framework of tagged cardiac MRI,

it could be of primary interest for the method to be

able to adapt the value of α to the fading of the tags

due to the non persistency of the magnetization corre-

sponding to the grid (see Fig. 1). More precisely, the

fact that this fading phenomenon can be analytically

studied would permit such an adaptive setting of α.

Moreover, if in this example we choose to select the

gradient-level, one could also think about integrating

a selectivity upon the grey-level to diffuse or not. This

can be achieved by considering a variant of Eq. (11)

given by

∂ψ

∂t

= c

div(c

(||A.∇ψ||)∇ψ) . (12)

In this equation, c

, as shown in this article, permits

a selectivity regarding gradient-level, and c

could

permit a selectivity in terms of grey-level intensity.

Considering the fact that the grey-level intensity of the

myocardium is different from the grey-level intensity

of the tags, this approach could be a good alternative

for enhancement of tagged cardiac MRI, but also for

MR images in general.

MRI IMAGE ENHANCEMENT - A PDE-based Approach Integrating a Double-well Potential Function for Thin Structure

Preservation

507

REFERENCES

Alvarez, L., Guichard, F., Lions, P., and Morel, J. (1992).

Image selective smoothing and edge detection by non-

linear diffusion (ii). Arch. Rationnal Mech. Anal.,

29(3):845–866.

Axel, L., Chung, S., and Chen, T. (2007). Tagged mri anal-

ysis using gabor ﬁlters. In Biomedical Imaging: From

Nano to Macro, 2007. ISBI 2007. 4th IEEE Interna-

tional Symposium on, pages 684–687.

Catt

e, F., Coll, T., Lions, P., and Morel, J. (1992). Im-

age selective smoothing and edge detection by nonlin-

ear diffusion. SIAM Journal of Applied Mathematics,

29(1):182–193.

Denney, T. (1999). Estimation and detection of myocar-

dial tags in MR images without user-deﬁned myocar-

dial contours. IEEE Transactions on Medical Imag-

ing, 18(4):330–344.

Deriche, R. and Faugeras, O. (1996). Les edp en traitements

des images et visions par ordinateur. Traitement du

Signal, 13(6):551–578.

Geman, S. and Reynolds, G. (1992). Constrained restora-

tion and the recovery of discontinuities. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

14(3):367–383.

Histace, A., Cavaro-M

enard, C., Courboulay, V., and

enard, M. (2005). Analysis of tagged cardiac MRI

sequences. Lecture Notes on Computer Science (Pro-

ceedings of the 3rd Functional Imaging and Mod-

elling of the Heart (FIMH) Workshop), 3504:404–

413.

Histace, A., M

enard, M., and Cavaro-M

enard, C. (2009).

Selective diffusion for oriented pattern extraction: Ap-

plication to tagged cardiac mri enhancement. Pattern

Recognition Letters, 30(15):1356–1365.

Nitzberg, M. and Shiota, T. (1992). Nonlinear image ﬁlter-

ing with edge and corner enhancement. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

14(8):826–833.

Perona, P. and Malik, J. (1990). Scale-space and edge

detection using anistropic diffusion. IEEE Transca-

tions on Pattern Analysis and Machine Intelligence,

12(7):629–639.

Petitjean, C., Rougon, N., and Cluzel, P. (2005). Assess-

ment of myocardial function: A review of quantiﬁca-

tion methods and results using tagged MRI. Journal of

Cardiovascular Magnetic Resonance, 7(2):501–516.

Rao, A. and Jain, R. (1992). Computerized ﬂow ﬁeld anal-

ysis: Oriented texture ﬁelds. Transactions on pattern

analysis and machine intelligence, 14(7).

Terebes, R., Lavialle, O., Baylou, P., and Borda, M. (2002).

Mixed anisotropic diffusion. In Proceedings of the

16th International Conference on Pattern Recogni-

tion, volume 3, pages 1051–4651.

Tschumperle, D. and Deriche, R. (2005). Vector-valued im-

age regularization with pde’s: A common framework

for different applications. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 27:506–517.

Tshumperl

e, D. and Deriche, R. (2002). Diffusion PDEs on

vector-valued images. Signal Processing Magazine,

IEEE, 19(5):16–25.

Weickert, J. (1995). Multiscale texture enhancement. In

Computer Analysis of Images and Patterns, pages

230–237.

Weickert, J. (1998). Anisotropic Diffusion in image process-

ing. Teubner-Verlag, Stuttgart.

Whitaker, R. and Pizer, S. (1993). A multi-scale approach to

nonuniform diffusion. CVGIP:Image Understanding,

57(1):99–110.

Zerhouni, E., Parish, D., Rogers, W., Yang, A., and Shapiro,

E. (1988). Human heart : tagging with MR imaging

- a method for noninvasive assessment of myocardial

motion. Radiology, 169(1):59–63.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

508