
EFFICIENT LEARNING OF DYNAMIC BAYESIAN NETWORKS
FROM TIMED DATA
Ahmad Ahdab and Marc Le Goc
LSIS, UMR CNRS 6168, Université Paul Cézanne, Domaine Universitaire St Jérôme, 13397 Marseille cedex 20, France
Keywords: Machine Learning, Bayesian network, Stochastic representation, Data mining, Knowledge discovery.
Abstract: This paper addresses the problem of learning a Dynamic Bayesian network from timed data without prior
knowledge to the system. One of the main problems of learning a Dynamic Bayesian network is building
and orienting the edges of the network avoiding loops. The problem is more difficult when data are timed.
This paper proposes an algorithm based on an adequate representation of a set of sequences of timed data
and uses an information based measure of the relations between two edges. This algorithm is a part of the
Timed Observation Mining for Learning (TOM4L) process that is based on the Theory of the Timed
Observations. The paper illustrates the algorithm with an application on the Apache system of the
Arcelor-Mittal Steel Group, a real world knowledge based system that diagnoses a galvanization bath.
1 INTRODUCTION
This paper describes the BJM4BN algorithm (BJ-
Measure for Bayesian Networks) that learns a
Dynamic Bayesian networks from timed data
without prior knowledge to the process that
generates the timed data. Most of the contributions
to learn a bayesian network are based on un-timed
data. The main difficulties are orienting the edges of
the resulting graph and building the conditional
probability tables. These problems are more difficult
when data are timed.
The BJM4BN algorithm proposes an efficient
solution to solve these problems when data are
timed. The solution is based on a particular
representation of the timed data called the Stochastic
Representation. These representation is the basis of
the theory of Timed Observations (Le Goc, 2006).
This theory defines a learning process called Timed
Observation Mining for Learning (TOM4L) (Le
Goc, 2005). The TOM4L process aims at
discovering temporal knowledge about a set of time
functions xi(t) considered as a dynamic system
X(t)={x
i
(t)} called a process. To this aim, the theory
of Timed Observations defines an entropic measures
called the the BJ-Measure of (Benayadi, 2008) that
evaluates the flow of information between two nodes
in a graph and provides so an efficient mean to
orient the edges.
The next section presents a very short state of the
art about learning Dynamic Bayesian networks
(DBN). Section 3 introduces the basis of the
Stochastic Representation of TOM4L and the BJ-
Measure. Section 4 describes the BJM4BN
algorithm and section 5 shows a real life application
of the algorithm. Section 6 concludes the paper.
2 RELATED WORKS
A BN is a couple <G, θ> where G denotes a Direct
Acyclic Graph in which the nodes represent the
variables and the edges represent the dependencies
between the variables (Pearl, 1988), and θ is the
Conditional Probabilities Tables (CP Tables)
defining the conditional probability between the
values of a variable given the values of the upstream
variables of G. BN learning algorithms aims at
discovering the couple <G, θ> from a given data
base. BN learning algorithms fall into two main
categories: “search and scoring” and “dependency
analysis” algorithms. The “search and scoring”
learning algorithms can be used when the knowledge
of the edge orientation between the variables of the
system is given (Cooper, 1992), (Heckerman, 1997).
To avoid this problem, dependency analysis
algorithms uses conditional independence tests
(Cheng, 1997), (Cheesseman, 1995), (Friedman
1998), (Meyrs et al, 1999). But the number of test
exponentially increases the computation time
226
Ahdab A. and Le Goc M. (2010).
EFFICIENT LEARNING OF DYNAMIC BAYESIAN NETWORKS FROM TIMED DATA.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
226-231
DOI: 10.5220/0002897802260231
Copyright
c
SciTePress

(Chickering, 1994).
For example, Cheng’s algorithm (Cheng, 1997)
for learning BN is based on the d-separation concept
of (Pearl, 1988) to infer the structure G of the
Bayesian Network, and the mutual information I(X,
Y) (eq. 1) to detect conditional independence
relations.
()
(
)
()
()
ji
ji
ji
ji
yYPxXP
yYxXP
yYxXPYXI
==
==
===
∑
,
log,),(
,
(1)
The mutual information I(X, Y) is used to
evaluate all the potential pairs of variables (X, Y) and
to producing a list L sorted in descending order:
pairs of higher mutual information are supposed to
be more related than those having low mutual
information values. The List L is then pruned given
an arbitrary parameter
ε
: each pair (X, Y) so that
I(X, Y)<
ε
is eliminated of L. In real world
applications, list L should be as small as possible
using the
ε
parameter. The two main limitations such
approaches is the need of defining the
ε
parameter
and the exponential amount of Conditional
Independence tests to orient the edges of the graph.
3 TOM4L FRAMEWORK
The BJM4BN algorithm provides a solution to these
two problems that is based on the Stochasxtic
Representation of the TOM4L framework (Le Goc,
2005), (Le Goc, 2006), (Le Goc, 2008).
In this framework, a message timed at t
k
contained in a database is an occurrence C
i
(k) of an
observation class C
i
={(x
i
,
δ
i
)} which is an arbitrary
set of couples (x
i
,
δ
i
) where
δ
i
is one of the discrete
value of a variable x
i
. An observation class is often a
singleton because in that case, two classes C
i
= {(x
i
,
δ
i
)} and C
j
= {(x
j
,
δ
j
)} are only linked with the
variables x
i
and x
j
when the constants
δ
i
and
δ
j
are
dependent (Le Goc, 2006). in
The Stochastic Representation of a sequence
ω=(…, C
i
(k), …) of m occurrences C
i
(k) defining a
set Cl={ C
i
} of n timed observations is a set of
matrix (Le Goc, 2005), (Bouché, 2005) from which
the BJ-Measure is computed (Benayadi, 2008). This
measure is based on the Kullback-Leibler distance
D(P(Y|X=C
i
)||P(Y)) that evaluates the relation
between the distribution of the conditional
probability of Y knowing that X = C
i
and the prior
probability distribution of Y. The BJ-measure
decomposes the Kullback-Leibler distance in two
terms around the independence point
P(Y|X=C
i
)=P(Y) (i.e. D(P(Y|X=C
i
)||P(Y)) = 0).
The BJL-measure BJL(C
i
→C
j
) of binary relation
r(C
i
→C
j
) is the right part of the Kullback-Leibler
distance D(P(Y|X=C
i
)||P(Y)) so that:
• P(Y=C
j
|X=C
i
)<P(Y=C
j
) ⇒ BJL(C
i
, C
j
)=0
• P(Y=C
j
|X=C
i
)≥P(Y=C
j
) ⇒
BJL(C
i
→C
j
)= D(P(Y|X=C
i
)||P(Y))
The BJL(C
i
→C
j
) is not null when the observation
C
i
(k) provides some information about the
observation C
j
(k). Symmetrically, when
BJL(C
i
→C
j
)<0, the observation C
i
(k) provides some
information about ¬C
j
(k). The BJL-measure
BJL(C
i
→¬C
j
) of a binary relation r(C
i
→¬C
j
) is then
the left part of the Kullback-Leibler distance:
• P(Y=C
j
|X=C
i
)<P(Y=C
j
) ⇒
BJL(C
i
→¬C
j
)=D(P(Y|X=C
i
)||P(Y))
• P(Y=C
j
|X=C
i
)≥P(Y=C
j
) ⇒ BJL(C
i
→¬C
j
)= 0
Consequently:
D(P(Y|X=C
i
)||P(Y))=BJL(C
i
→C
j
)+BJL(C
i
→¬C
j
)
(2)
Similarly, the BJW-measure evaluates the
information distribution between the predecessors
(C
i
(k) or ¬C
i
(k)) of an observation C
j
(k+1) at time
t
k+1
:
D(P(X|Y=C
j
)||P(X))=BJW(C
i
→C
j
)+BJW(C
i
→¬C
j
)
(3)
Because (P(C
j
|C
i
)<P(C
j
))⇔P(C
i
|C
j
)<P(C
i
)), the
two measures are null at the same independence
point and can be combined in a single measure
called the BJM-measure which is the norm vector of
BJL(C
i
→C
j
) and BJW(C
i
→C
j
):
M(C
i
→C
j
)=
22
),(),(
jiji
CCBJWCCBJL +
–
22
),(),(
jiji
CCBJWCCBJL ¬+¬
(4)
The BJ-Measure is no more justifiable when the
θ
i,j
= n
i
/n
j
is greater of 4 or less than ¼ (Benayadi,
2008). This property is called the
θ
property.
When a BJ-measure M(C
i
→C
j
) is positive, the
timed observation distribution of the C
i
class bring
information about the timed observation distribution
of the C
j
class. So, considering the positive values
only, the BJ-measure M(C
i
→C
j
) satisfies the three
following properties:
1. Dissymmetry:
M(C
i
→C
j
)≠M(C
j
→C
i
) (generally)
2. Positivity: ∀ C
i
, C
j
, M(C
i
→C
j
) ≥ 0
3. Independence:
M(C
i
→C
j
)=0 ⇔ C
i
and C
j
are independant (i.e.
P(C
j
|C
i
)=P(C
j
))
4. Triangular inequality:
M(C
i
→C
j
) < M(C
i
→C
k
) + M(C
k
→C
j
)
This latter property can be used to reason with
the BJ-measure to deduce the structure of a dynamic
Bayesian network.
EFFICIENT LEARNING OF DYNAMIC BAYESIAN NETWORKS FROM TIMED DATA
227
4 LEARNING PRINCIPLES
Let us consider a set R={…, r(C
i
→C
j
), …} of n
binary relations. The operation that remove a binary
relation r(C
i
→C
j
) from the set R is denoted
Remove(r(C
i
→C
j
)): R ← R – { r(C
i
→C
j
) }.
The positivity property leads to remove the
r(C
i
→C
j
) relations having a negative value of the
BJ-measure:
• Rule 1 (“Positivity rule”):
∀r(C
i
→C
j
)∈R, M(C
i
→C
j
)≤0 ⇒
Remove(r(C
i
→C
j
))
The dissymmetry property allows deducing the
orientation of a hypothetical relation between two
timed observation classes C
i
and C
j
:
• Rule 2 (Orientation rule):
∀r(C
i
→C
j
), r(C
j
→C
i
)∈R,
M(C
i
→C
j
)>M(C
j
→C
i
) ⇒ Remove(r(C
j
→C
i
))
C
i+1
C
i
BJM(C
i
→C
i+1
)
C
j
BJM(C
i+1
→C
i+2
)
BJM(C
j
→C
i
)
C
i+2
C
i+n
BJM(C
i+n
→C
j
)
…
C
i+1
C
i
BJM(C
i
→C
i+1
)
C
j
BJM(C
i+1
→C
i+2
)
BJM(C
j
→C
i
)
C
i+2
C
i+n
BJM(C
i+n
→C
j
)
…
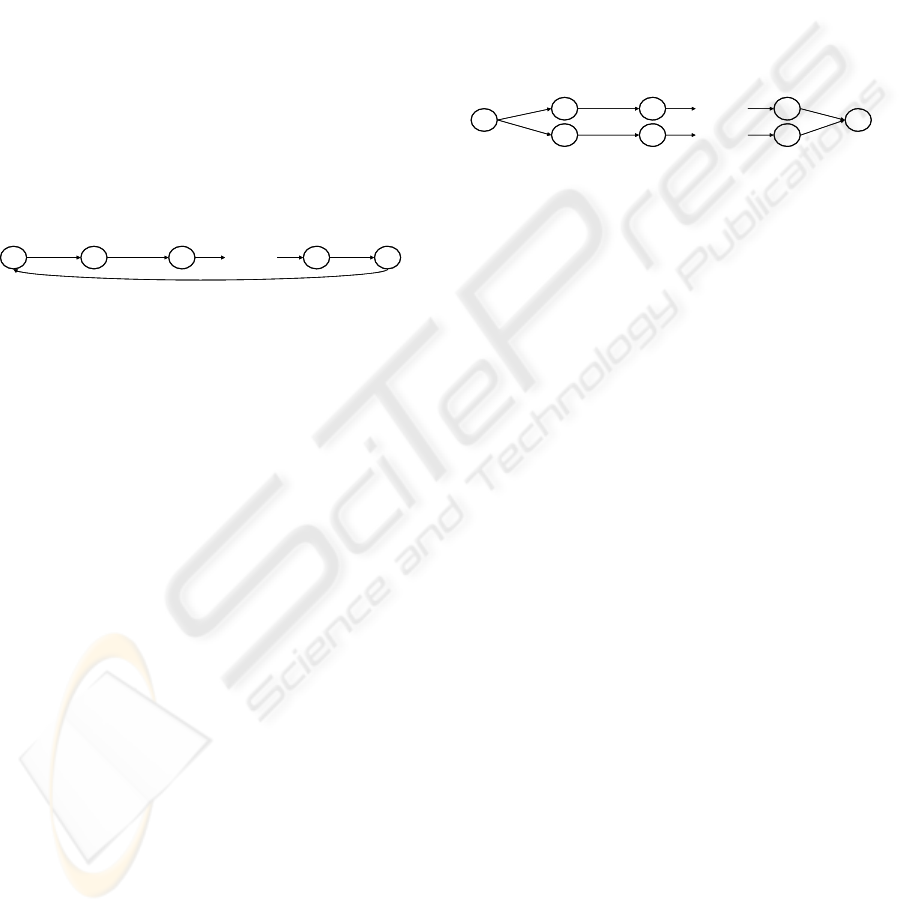
Figure 1: Loops.
Now, let us consider a set R={r(C
i
→C
i+1
),
r(C
i+1
→C
i+2
), ..., r(C
i+n
→C
j
), r(C
j
→C
i
)} of n+2
binary relations defining a loop (Figure 2) where:
• ∀r(C
x
→C
y
) ∈ R, M(C
x
→C
y
) > 0
The problem of the set R is that computing the
distribution of a class C
x
requires knowing its
distribution: loops must then be avoided. In other
words, a relation r(C
i
→C
j
) must be removed from R
to break the loop. To solve this problem, the idea is
to used the monotonous property of the BJ-measure:
finding two of class C
i
and C
j
so that the BJ-measure
of the relation r(C
i
→C
j
) is the lowest of the loop:
• Rule 3 (Loop Rule):
∀r(C
x
→C
y
)∈R, ∃r(C
i
→C
j
)∈R, x≠i, y≠j,
M(C
x
→C
y
)>M(C
i
→C
j
) ⇒ Remove(r(C
i
→C
j
))
When M(C
x
→C
y
)=M(C
i
→C
j
)), any of the
relations can be removed. The extreme case of loop
is can be find in a set R containing a reflexive
relation r(C
i
→C
i
) where M(C
i
→C
i
)>0. Rule 3 must
then be adapted to this extreme (but frequent) case:
• Rule 4 (Reflexivity rule):
∀r(C
i
→C
i
) ∈ R, M(C
i
→C
i
) > 0 ⇒
Remove( r(C
i
→C
i
) )
Finally, to build naïve Bayesian Networks, the
algorithm must avoid the multiple paths leading to a
same C
i
class (Figure 3). To avoid this problem, the
idea is to use the monotonous property of the BJ-
measure: finding two of class C
i
and C
j
so that the
BJ-measure of the relation r(C
i
→C
j
) is the lowest of
the paths. To use this idea, all the paths leading to a
particular C
i
class must be find in R. Let us suppose
that R contains n paths R
1
⊆R, R
2
⊆R, …, R
n
⊆R
leading to the C
i
class (i.e. each R
i
is of the form
R
i
={r(C
i
→C
k-n
), r(C
k-n
→C
k-n+1
), ..., r(C
k
→C
j
),
r(C
i
→C
l-n
), r(C
l-n
→C
l-n+1
), r(C
l
→C
j
)}. The algorithm
must find the r(C
i
→C
j
) relation with the lowest BJ-
measure to remove it in R (“Transitivity rule”):
• Rule 5 (Transitivity rule):
∀r(C
x
→C
y
)∈R
1
∪R
2
∪…∪R
n
,
∃r(C
i
→C
j
) ∈ R
1
∪R
2
∪…∪R
n
, x≠i, y≠j,
M(C
x
→C
y
)>M(C
i
→C
j
)⇒Remove(r(C
i
→C
j
))
C
k-n
C
i
C
j
C
k-n-1
C
k
…
C
l-m
C
l-m-1
C
l
…
C
k-n
C
i
C
j
C
k-n-1
C
k
…
C
l-m
C
l-m-1
C
l
…
Figure 2: Multiple Paths.
These five rules are necessary (but no sufficient)
to design an algorithm, but its efficiency depends
mainly of the number of relation in the initial set R.
The TOM4L framework provides the mathematical
tools to remove the relations that can not play a
significant role in the building of a naïve Bayesian
Network. Given the set R={…, r(C
i
→C
j
), …} of n
binary relations that can be build from a sequence
ω
of timed observation C
i
(k) defining a set C={C
x
} of
N(C) classes C
x
. The size of the Stochastic
Representation matrix of the TOM4L framework is
then N(C)
⋅
N(C)=N(C)
2
. This provides two ways to
eliminate a relation r(C
i
→C
j
) having no interest for
building a naïve Bayesian Network:
• Test 1: P(C
j
|C
i
)⋅P(C
i
, C
j
)≤1/N(C)
3
⇒ Remove(r(C
i
→C
j
))
This first test compares b
ij
≡P(C
j|
C
i
)⋅P(C
i
, C
j
)
with the hazard of having an occurrence C
i
(k) of the
C
i
class at time t
k
knowing that there is an
occurrence C
j
(k+1) of the C
j
class occurring at time
t
k+1
. Because
ω
defines N(C) classes, the a priori
probability of having an occurrence C
i
(k) of a C
i
class followed by an occurrence C
j
(k+1) of the C
j
class is P(C
j
|C
i
)=1/N(C) and the probability of
reading a couple (C
i
(k), C
j
(k+1)) in
ω
is P(C
i
, C
j
)=
1 / N(C)
2
. So each b
ij
value can be compared with
the “absolute” hazard 1 / (N(C) N(C)
2
).
• Test 2: P(C
j
|C
i
)⋅P(C
i
, C
j
)≤(1/(N(C)⋅P(C
i
)⋅P(C
j
))
⇒ Remove(r(C
i
→C
j
))
This second test defines the hazard when
supposing that C
i
and C
j
classes are independent. In
that case, the probability P((C
j
(k), C
i
(k+1)) in
ω
of
having a couple (C
i
(k), C
j
(k+1)) in
ω
is P(C
i
)⋅P(C
j
)
and having an occurrence C
i
(k) of a C
i
class, the
hazard is to read any occurrence C
j
(k+1) of the C
j
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
228

class: P(C
j
|C
i
)=1/N(C). So each b
ij
value can be
compared with the “relative” hazard
1/(N(C)⋅P(C
i
)⋅P(C
j
)).
The
θ
property of the BJ-measure complete these
two tests to eliminate the relation having no meaning
according to the BJ-measure:
• Test 3:
θ
i,j
>4 ∨
θ
i,j
<1/4 ⇒ Remove(r(C
i
→C
j
))
Within the TOM4L framework, these tree tests
are implemented in the F0/1=[f
ij
] matrix:
• (b
ij
>1/N(C)
3
) ∧ (b
ij
>(1/(N(C)⋅P(C
i
)⋅P(C
j
)) ∧ (1/4
≤
θ
i,j
≤ 4) ⇔ f
ij
= 1
So this lead to the rule number 6:
• Rule 6: ∀r(C
i
→C
j
)∈R,
f
ij
= 0 ⇒ Remove( r(C
i
→C
j
) )
These six rules are used by the BJM4BN
algorithm to build a naïve Bayesian Network.
5 THE BJM4BN ALGORITHM
The BJM4BN algorithm takes as inputs a sequence
ω of m timed observation C
i
(k) defining a set
Cl={C
x
} of N(Cl) classes C
x
and an output C
j
class
that is the class for which the DBN is computed. It
produces a set G={…, r(C
i
→C
j
), …} of n binary
relations that form the structure of a naïve Bayesian
Network (G,
Θ
).
The “BJM4BN” algorithm contains 5 stages. The
first stage computes the Stochastic Representation of
Θ
to produce the initial M=[m
ij
] matrix containing
the BJ-measure values of the N(Cl)
2
binary relations
r(C
i
→C
j
)) defined by ・ (line 1).
// Stage 1
1. Compute the M=[m
ij
] matrix
2. ∀i=0…N(Cl), ∀j=0…N(Cl), f
ij
=0
3. ∀i=0…N(Cl), ∀j=0…N(Cl),
(b
ij
>1/N(C)
3
)∧(b
ij
>(1/(N(C)⋅P(C
i
)⋅P(C
j
))
∧(1/4≤
θ
i,j
≤ 4) ⇒ f
ij
=1
4. M=M⋅F0/1
5. ∀i=0…N(Cl), ∀j=0…N(Cl),
5.1. m
ij
≤0 ⇒ m
ij
=0 // rule 1
5.2. i=j ⇒ m
ij
=0 // rule 4
Next, the F0/1=[f
ij
] matrix is computed using
test 4 (line 3) so that the new values m
ij
=m
ij
⋅f
ij
of
matrix M=[m
ij
] with rule 6 (line 4). Finally, the M
matrix is normalized using rules 1 (line 5.1) and 4
(line 5.2).
// Stage 2
6. L={
φ
}
7. ∀i=0…N(Cl), ∀j=0…N(Cl), m
ii
>0,⇒
L=L+{(r(C
i
→C
j
), m
ii
)}
Stage 2 computes the list L from the normalized
matrix M. The list L={(r(C
i
→C
j
), m
ii
)} contains
couples of the form (r(C
i
→C
j
), m
ii
) where m
ii
is
the BJ-measure value of the associated r(C
i
→C
j
)
binary relation. This list will be used to find the
relation r(C
x
→C
y
) so that m
xy
is the minimal value
of the BJ-measures contained in L.
// Stage 3
8. C
x
=C
j
, G={
φ
}
9. ∀r(C
y
→C
x
))∈L ⇒ G=G+{r(C
y
→C
x
)}
10. Build(G, C
x
){
∀r(C
y
→C
x
))∈G, ∀r(C
z
→C
y
))∈L,
G=G+{r(C
z
→C
y
)}
Build(G, C
y
)
}// End Build Function
Stage 3 builds recursively the initial G graph
from the C
j
class. This stage uses a recursive
function called “Build(G, C
x
)” where C
x
is the class
the graph of which is to build.
// Stage 4
11. R={
φ
}
12. ∀R
i
⊆G, R
i
≡{r(C
i
→C
i+1
), r(C
i+1
→C
i+2
), ...,
r(C
i+n
→C
j
), r(C
j
→C
i
)} ⇒ R=R+{R
i
}
13. ∀R
i
∈R, ∀r(C
x
→C
y
)∈R
i
, r(C
x
→C
y
)∉L
1
⇒
L
1
=L
1
+{(r(C
x
→C
y
), m
xy
)}
14. While R≠{
φ
} repeat
. ∃r(C
x
→C
y
)∈L
1
, m
xy
= Min(m
ij
, L
1
)
∀R
i
∈R, ∃r(C
x
→C
y
)∈R
i
⇒
R=R-{R
i
}
G=G–{r(C
x
→C
y
)}
L
1
=L
1
-{(r(C
x
→C
y
), m
xy
)}
Stage 4 finds and removes the loops in G with
Rule 3. This stage finds all the loops R
i
in G of the
form R
i
≡{r(C
i
→C
i+1
), r(C
i+1
→C
i+2
), ..., r(C
i+n
→C
j
),
r(C
j
→C
i
)} and put them in a set R (line 12). Next, a
new list L
1
is build containing all the relation
r(C
x
→C
y
) in R with its associated m
xy
BJ-measure
value (line 13). Every loops R
i
in R are then removed
using Rule 3 and the resulting G graph is updated
(line 14). At the end of this stage, G contains no
more loops. It is to note that the L
1
list being global
(i.e. containing all the relations r(C
x
→C
y
)
participating in a loop), it is guaranty that the set of
removed relation r(C
x
→C
y
) is optimal: it is minimal
and the removed relations are the smallest of the G
graph.
//Stage 5
15. R={
φ
}
16. ∀R
i
⊆G,
R
i
≡{r(C
i
→C
k-n
), r(C
k-n
→C
k-n+1
), ...,
r(C
k
→C
j
), r(C
i
→C
l-n
), r(C
l-n
→C
l-n+1
), ...,
r(C
l
→C
j
)} ⇒ R=R+{R
i
}
17. ∀R
i
∈R,
∀r(C
x
→C
y
)∈R
i
, r(C
x
→C
y
)∉L
1
⇒
L
1
=L
1
+{(r(C
x
→C
y
), m
xy
)}
18. While R≠{
φ
} repeat
∃r(C
x
→C
y
)∈L
1
, m
xy
= Min(m
ij
, L
1
)
∀R
i
∈R, ∃r(C
x
→C
y
)∈R
i
⇒
R=R-{R
i
}
G=G–{r(C
x
→C
y
)}
L
1
=L
1
-{(r(C
x
→C
y
), m
xy
)}
EFFICIENT LEARNING OF DYNAMIC BAYESIAN NETWORKS FROM TIMED DATA
229
Stage 5 removes the multiple paths in the G
graph with Rule 5. This stage proceeds as the stage
4, but the R set contains only paths R
i
of the form
R
i
≡{r(C
i
→C
k-n
), r(C
k-n
→C
k-n+1
), ..., r(C
k
→C
j
),
r(C
i
→C
l-n
), r(C
l-n
→C
l-n+1
), ..., r(C
l
→C
j
)} (line 16).
At the end of this stage, G contains no more multiple
paths and it is guaranty that the set of removed
relation r(C
x
→C
y
) is optimal.
Stage 6 computes the conditional probabilities
tables for G and finalizes the algorithm. The
computing of the Conditional Probabilities Tables
(CP Tables) is based on the numbering table N=[n
ij
]
of the Stochastic Representation of the ω sequence:
• P(Y=C
o
| X=C
i
) + P(Y=¬C
o
| X=C
i
) = 1.
The computing of the CP tables uses this
property (for simplicity, P(C
y
|C
x
) is rewritten P(y|x)).
For a root node C
x
:
• P(x)=(Σ
j
n
xj
) / Σ
i
Σ
j
n
ij
For a single relation r(C
x
→C
y
):
• P(y|x) = n
xy
/ (Σ
j
n
yj
)
• P(y|¬x) = (Σ
i
n
iy
)-n
xy
) / (Σ
i
Σ
j
n
ij
–(Σ
j
n
xj
))
For a set R={r(C
x
→
jy
), r(C
z
→C
y
)} of two
relations converging to the same C
y
class:
• P(y|x,z) = (n
xy
+n
zy
) / (Σ
j
n
xj
+Σ
j
n
zj
)
• P(y|¬x,z) = (Σ
i
n
iy
-n
xy
) / (Σ
i
Σ
j
n
ij
-Σ
j
n
xj
)
• P(y|x,¬z) = (Σ
i
n
iy
-n
zy
) / (Σ
i
Σ
j
n
ij
-Σ
j
n
zj
)
• P(y |¬x,¬z) = (Σ
i
n
iy
-n
xy
-n
zy
) / (Σ
i
Σ
j
n
ij
-Σ
j
n
xj
-Σ
j
n
zj
)
The next section illustrates the computation of
the CP tables with a real world process.
6 REAL WORLD APPLICATION
The Apache system is a clone Sachem, the
knowledge based systems that The Arcelor Group,
one of the most important steal companies in the
world, has developed to monitor and diagnose its
production tools (Le Goc, 2004). Apache aims at
controlling a zinc bath, a hot bath containing a liquid
mixture of aluminum and zinc continuously fed with
aluminum and zinc ingots in which a hot steel strip
is immerged. Apache monitors and diagnoses around
11 variables and is able to detect around 24 types of
alarms. The analyzed sequence ω contains 687
events of 13 classes for 11 discrete variables. The
counting matrix N contains then 156 cells n
ij
(Table
1). The corresponding M matrix is provided in Table
2, the F0/1 matrix in Table 3 and the normalized M
matrix in Table 4. These matrixes are computed in
the first stage of the “BJM4BN” algorithm.
The stage 2 computes the L list of Table 5. The
node of interest being 1006, the initial G graph
resulting of stage 3 of the “BJM4BN” algorithm is
given in Figure 4. This stage uses the normalized M
matrix and start with the 1006 column to add the
relations r(1001, 1006) and r(1001, 1006) in the
initial G. graph. Next, the Build(G, 1006) function is
executed to add the relation r(1004, 1001) in G
before calling Build(G, 1001) function and so on.
Table 1: Counting matrix N of ω.
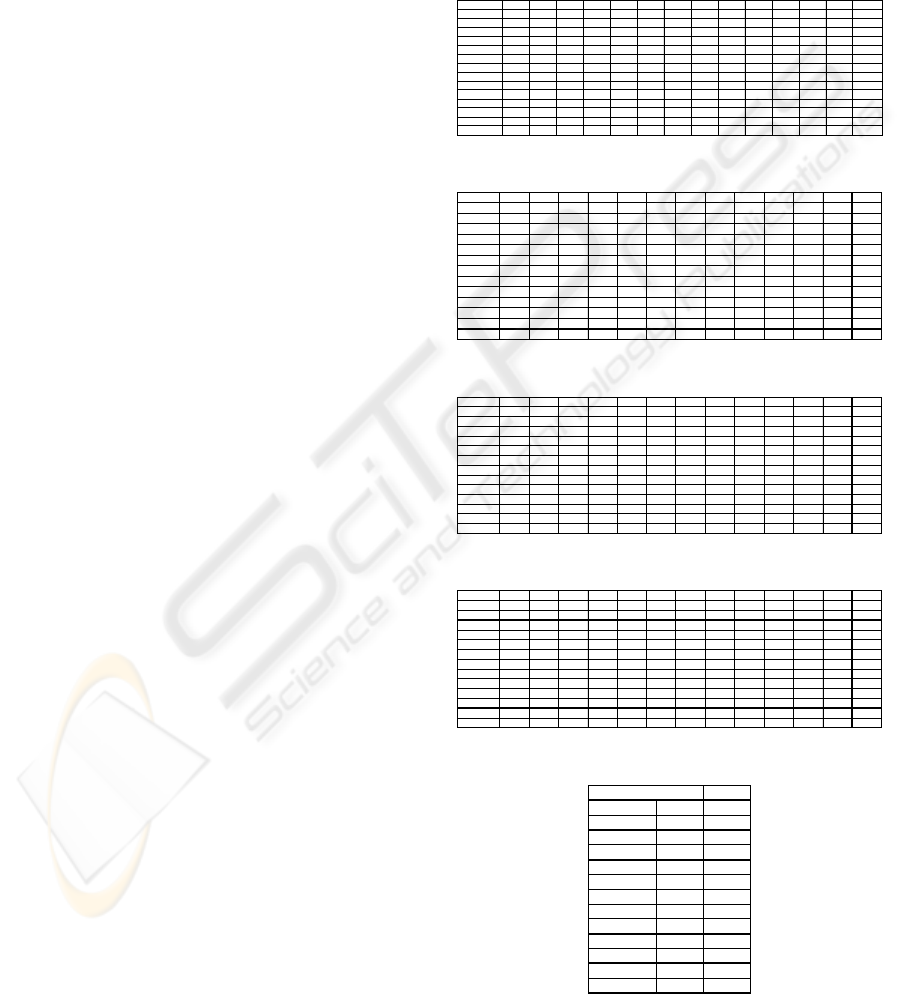
N 1001 1002 1004 1006 1014 1020 1022 1024 1025 1026 1029 1031 1037 TOTAL
1001
620150100604503
1002
411410000002402
1004
24020200301311
1006
10 5 7 35 1 15 1 6 20 4 21 23 0 148
1014
01040000140001
1020
1221805016251005
1022
0001000100200
1024
10230300216702
1025
2432207262633412112
1026
00080401200201
1029
4121507033931413010
1031
9622106171911136212
1037
0000010000210
9
6
8
0
2
4
5
2
7
1
1
39 26 19 148 11 51 4 25 124 18 102 116 4 68
4
7
Table 2: The M matrix of ω.
M 1001 1002 1004 1006 1014 1020 1022 1024 102
5
1026 1029 1031 1037
1001
0.0731 0.0104 -0.6851 0.0193 -0.7048 -0.1189 -0.7478 -0.6877 -0.0023 -0.6860 -0.0138 -0.0073 -0.7478
1002
0.0901 0.0000 0.0136 -0.0137 0.4975 -0.8044 -0.5332 -0.5741 -1.4754 -0.5351 -0.0572 -0.0010 -0.5332
100
4
0.0540 0.2722 -0.4630 -0.0678 -0.4035 0.0203 -0.3894 -0.5242 -0.0008 -0.4539 -0.1494 0.0000 0.7084
1006
0.0022 -0.0014 0.0279 0.0002 -0.1357 0.0053 0.0039 0.0012 -0.0032 0.0001 -0.0001 -0.0002 -2.0168
101
4
-0.7094 0.1322 -0.4136 0.0476 -0.3017 -0.8745 -0.2377 -0.5036 -0.0625 0.5957 -1.4682 -1.6083 -0.2377
1020
-0.1232 0.0000 0.0135 0.0107 -0.8802 0.0054 -0.9419 -0.0496 -0.0170 0.0185 -0.0164 0.0011 -0.9419
1022
-0.7478 -0.5332 -0.4079 0.0039 -0.2569 -0.9276 -0.1304 0.5404 -1.7875 -0.3894 0.2021 -1.7067 -0.1304
102
4
-0.0146 -0.5741 0.1290 -0.0457 -0.5041 0.0244 -0.5157 -0.5667 -0.0925 0.0226 0.0211 0.0225 -0.5157
1025
-0.1857 -0.0024 -0.0018 -0.0011 -1.6506 -0.0053 0.1506 0.0088 0.0008 -0.0005 0.0095 -0.015
2
0.0204
102
6
-0.6874 -0.5312 -0.4549 0.0557 -0.3895 0.1293 -0.3708 0.0294 -0.0276 -0.4451 -1.3792 -0.0194 -0.3708
1029
-0.0131 -0.2437 -0.0158 -0.0065 -1.4442 -0.0004 -1.5483 -0.0050 0.0124 0.0020 -0.0002 -0.0037 -1.5483
1031
0.0053 0.0070 -0.0390 -0.0017 -1.6411 -0.0138 0.0214 0.0191 -0.0007 -0.2127 -0.0132 0.0073 0.1528
1037
-0.7478 -0.5332 -0.4079 -2.0168 -0.2569 0.2355 -0.1304 -0.5157 -1.7875 -0.3894 0.2021 0.0268 -0.1304
Table 3: The F0/1 matrix of ω.
F0/1
1001 1002 1004 1006 1014 1020 1022 1024 1025 1026 1029 1031 1037
1001 1 1
1002 1 1
1004 1 1 1
1006 1 1 1
1014 1 1
1020 1 1 1
1022
1024 1 1
1025 11
1026 1 1
1029 1
1031 1 1
1037
Table 4: The normalized M matrix.
Normed M
1001 1002 1004 1006 101
4
1020 1022 1024 1025 1026 1029 1031 1037
1001 0.0193
1002 0.0901 0.4975
1004 0.0540 0.2722 0.0203
1006 0.0022 0.0053
1014 0.1322 0.5957
1020 0.0107 0.0011
1022
1024 0.1290 0.0244
1025 0.0095
1026 0.1293 0.0294
1029 0.0124
1031 0.0053
1037
Table 5: The L list of Stage 2.
M(i, j )
1014 1026 0.5957
1002 1014 0.4975
1004 1002 0.2722
1024 1004 0.1290
1002 1001 0.0901
1004 1001 0.0540
1026 1024 0.0294
1024 1020 0.0244
1004 1020 0.0203
1001 1006 0.0193
1020 1006 0.0107
1031 1001 0.0053
1020 1031 0.0011
r (i, j )
The G graph of Figure 3 having no loops, the
stage 4 modify noting and stage 5 is executed with
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
230
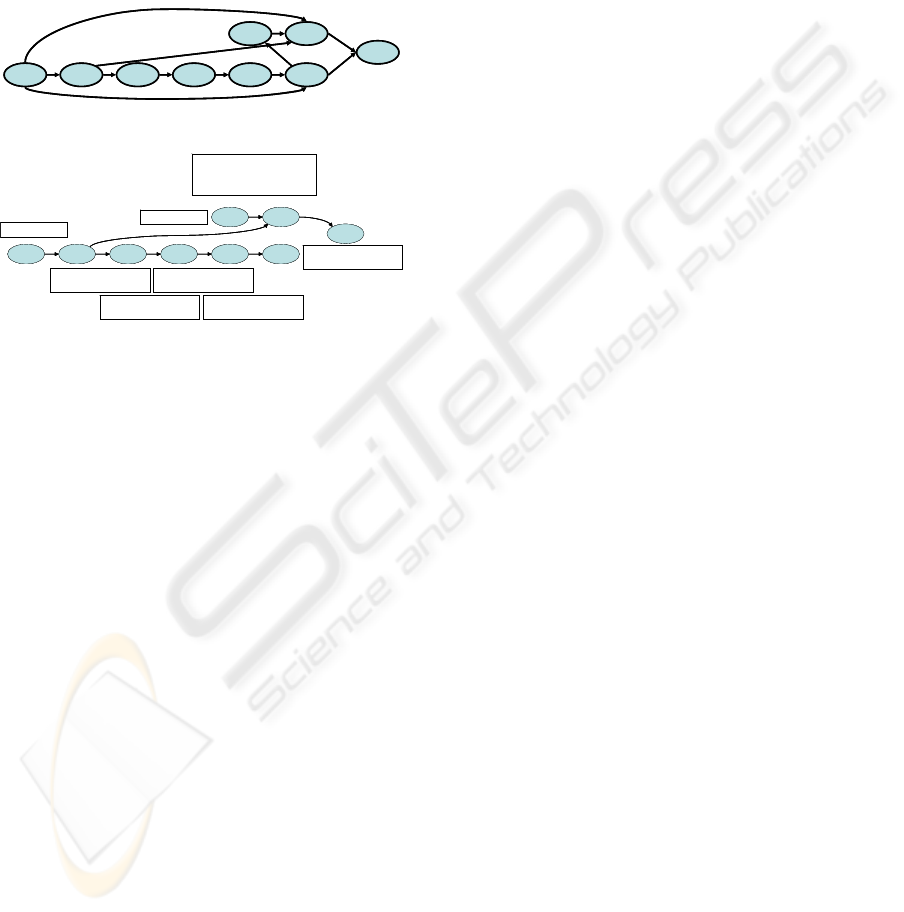
REFERENCES
this graph. Because each relation of the G graph
participates to the seven paths leading to the nodes
1006 and 1001, the L
1
list is equal to the L list of
Table 5. This table has been sorted so that the
minimal value m
ij
is at the end of the list. Its is then
easy to see that the relation r(1020, 1031) is the first
removed relation, before the relations r(1020, 1006)
and r(1004, 1001). The elimination of these three
relations is sufficient to build the final G graph of
Figure 4.
Benayadi, N., Le Goc, M., (2008). Discovering Temporal
Knowledge from a Crisscross of Timed Observations.
To appear in the proceedings of the 18th European
Conference on Artificial Intelligence (ECAI'08),
University of Patras, Patras, Greece.
Bouché, P., Le Goc, M., Giambiasi, N., (2005). Modeling
discrete event sequences for discovering diagnosis
signatures. Proceedings of the Summer Computer
Simulation Conference (SCSC05) Philadelphia, USA.
Cheeseman, P., Stutz, J., (1995). Bayesian classification
(Auto-Class): Theory and results. Advances in
Knowledge Discovery and Data Mining, AAAI Press,
Menlo Park, CA, p. 153-180.
1006
1001
1020
1031
10261004 10141002 1024
1006
1001
1020
1031
10261004 10141002 1024
Cheng, J., Bell, D., Liu, W., (1997). Learning Bayesian
Networks from Data An Efficient Approach Based on
Information Theory.
Figure 3: Initial G graph.
Cheng, J., Greiner, R., Kelly, J., Bell, D., Liu, W., (2002).
Learning Bayesian Networks from Data: An
Information-Theory Based Approach. Artificial
Intelligence, 137, 43-90.
P(1031) = 0,176
P(1004) = 0,026
P(1014 | 1002) = 0.385
P(1014 | ¬1002) = 0.024
P(1026 | 1014) = 0.400
P(1026 | ¬1014) = 0.010
P(1024 | 1026) = 0.059
P(1024 | ¬1026) = 0.025
P(1001 | 1031, 1002) = 0.088
P(1020 | 1031, ¬1002) = 0.053
P(1020 | ¬ 1031, 1002) = 0.053
P(1020 | ¬1031, ¬1002) = 0.048
P(1020 | 1024) = 0.120
P(1020 | ¬1024) = 0.033
P(1006 | 1001) = 0.385
P(1006 | ¬1001) = 0.037
1006
1001
1020
1031
10261004 10141002 1024
P(1031) = 0,176
P(1004) = 0,026
P(1014 | 1002) = 0.385
P(1014 | ¬1002) = 0.024
P(1026 | 1014) = 0.400
P(1026 | ¬1014) = 0.010
P(1024 | 1026) = 0.059
P(1024 | ¬1026) = 0.025
P(1001 | 1031, 1002) = 0.088
P(1020 | 1031, ¬1002) = 0.053
P(1020 | ¬ 1031, 1002) = 0.053
P(1020 | ¬1031, ¬1002) = 0.048
P(1020 | 1024) = 0.120
P(1020 | ¬1024) = 0.033
P(1006 | 1001) = 0.385
P(1006 | ¬1001) = 0.037
1006
1001
1020
1031
10261004 10141002 1024
1006
1001
1020
1031
10261004 10141002 1024
Chickering, D. M., Geiger, D., Heckerman, D., (1994).
Learning Bayesian Networks is NP-Hard. Technical
Report MSR-TR-94-17, Microsoft Research, Microsoft
Corporation.
Cooper, G. F., Herskovits, E., (1992). A Bayesian Method
for the induction of probabilistic networks from data.
Machine Learning, 9, 309-347.
Figure 4: Final G graph.
The CPT tables are computed using the N matrix
(table 1). This matrix provides all the information’s
to compute the probabilities of the root nodes of
figure 4. A handmade graph of the experts of the
Arcelor Group in 2003 can be find in (Bouché,
2005) and (Le Goc, 2005). The G graph is all
contained in the expert’s graph. But the expert’s
graph does not contain the 1024 class: corresponding
to an operator query for a chemical analysis, this
class has been removed by experts.
Friedman, N., (1998). The Bayesian structural EM
algorithm. Proceedings of the 14th Conference on
Uncertainty in Artificial Intelligence. Morgan
Kaufmann, San Francisco, CA, p. 129-138.
Heckerman, D., Geiger, D., Chickering, D. M., (1997).
Learning Bayesian networks: the combination of
knowledge and statistical data. Machine Learning
Journal, 20(3).
Le Goc, M., Bouché, P., and Giambiasi, N., (2005).
Stochastic modeling of continuous time discrete event
sequence for diagnosis. Proceedings of the 16th
International Workshop on Principles of Diagnosis
(DX’05) Pacific Grove, California, USA.
Le Goc, M., (2006). Notion d’observation pour le
diagnostic des processus dynamiques: Application a
Sachem et a la découverte de connaissances
temporelles. Hdr, Faculté des Sciences et Techniques
de Saint Jérôme.
7 CONCLUSIONS
This paper shows that the “BJT4BN” algorithm is
efficient both in terms of pertinence, simplicity and
speed. These properties come from the BJ-measure
that provides an operational way to orient the edges
of Bayesian Network without the exponential CI
Tests of Cheng’s method. It is then an advantage of
using the time of the data to learn a dynamic
Bayesian network. Our current works are concerned
with the combination of the Timed Data Mining
techniques of the TOM4L framework with the
“BJT4BN” algorithm to define a global validation of
the TOM4L learning process.
Myers, J., Laskey, K., Levitt, T., (1999). Learning
Bayesian Networks from Incomplete Data with
Stochastic Search Algorithms.
Pearl, J., (1988). Probabilistic Reasoning in Intelligent
Systems: Networks of Plausible Inference. San Mateo,
Calif.: Morgan Kaufmann.
EFFICIENT LEARNING OF DYNAMIC BAYESIAN NETWORKS FROM TIMED DATA
231
