A MULTIPHASE ACTIVE CONTOUR MODEL WITH DYNAMIC
MEDIAL AXIS CONSTRAINT FOR MEDICAL IMAGE
SEGMENTATION
Yan Zhang and Bogdan J. Matuszewski
Applied Digital Signal and Image Processing Research Centre, School of Computing Engineering and Physical Sciences
University of Central Lancashire, Preston PR1 2HE, U.K.
Keywords:
Medical image segmentation, Active contour, Shape constraint, Level-set, Multiphase segmentation.
Abstract:
A level-set based multiphase active contour model is proposed for medical image segmentation in this paper.
The proposed method allows multiple objects with very different features to be jointly segmented by simul-
taneously evolving multiple active contours, each responsible for the segmentation of a single object. In this
model, the forces exerted on each active contour mainly consists of two components. The first component
makes use of boundary as well as regional information present in the input images. The second component is
used to impose the so-called medial axis constraint, which is related to the force induced by interaction of mul-
tiple active contours. Experimental results on real medical images are also presented to show that the proposed
method has good performances on topology preservation of multiple contours, as well as joint segmentation
of similar objects in multiple images.
1 INTRODUCTION
Segmentation is a basic yet important problem in
medical image processing, which is widely used in
medical applications such as surgicalplanning, abnor-
mality detection and treatment progress monitoring.
Originally proposed in (Kass et al., 1988) as a tool
for image segmentation, active contour models have
attracted extensive research in the past two decades.
The basic idea of the active contour is to iteratively
evolve an initial curve towards the boundaries of the
target objects driven by the combination of internal
forces determined by the geometry of the evolving
curve and the external forces induced from the image.
Image segmentation method using active contour
is usually based on minimizing a functional which is
so defined that for curves close to the target bound-
aries it has small values. To solve the functional min-
imization problem, a corresponding partial differen-
tial equation (PDE) can be constructed as the Gateaux
derivative gradient flow to steer the evolution of the
active contour.
Either explicit or implicit method can be applied
to numerically approximate a curve evolution PDE.
For explicit methods, an active contour can be rep-
resented in parametric form such as linear and cubic
B-splines (Precioso et al., 2005). In that case, a finite
number of points are sampled on the active contour
and move according to the calculated forces, thereby
causing the evolution of the entire contour.
For implicit (or level set) methods, an active con-
tour is embedded as a constant level set (typically
level zero) in a function defined in a higher dimen-
sional space known as embedding function or level
set function. The evolution of the active contour is
carried out implicitly by the evolution of its embed-
ding function. Thanks to its inherent capability to
handle topological changes and straightforward ex-
tensibility to cope with high dimensional data, since
the pioneering work of (Malladi et al., 1995), level set
based segmentation has gained considerable research
attention and has prompted the development of a large
amount of models. Among these, two models, namely
geodesic active contour model (Caselles et al., 1997)
and Chan-Vese model (Chan and Vese, 2001), stand
out respectively as the paradigms for boundary-based
and region-based segmentation.
Most of the level-set algorithms in the aforemen-
tioned literature are focused on designing evolution
functions for a single level set. According to these
methods, although a single level set can embed mul-
tiple separate active contours, each active contour is
516
Zhang Y. and J. Matuszewski B. (2010).
A MULTIPHASE ACTIVE CONTOUR MODEL WITH DYNAMIC MEDIAL AXIS CONSTRAINT FOR MEDICAL IMAGE SEGMENTATION.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 516-521
DOI: 10.5220/0002917005160521
Copyright
c
 SciTePress

driven independently by the same evolution rule. To
simultaneously segment multiple objects with very
different features, multiphase methods have been pro-
posed to use more than one level set functions.
In (Brox and Weickert, 2006; Lankton and Tan-
nenbaum, 2008), the evolution rule for each level
set function consists of not only the traditional terms
derived from specific functionals, but also the extra
terms imposed by the proximity constraint. The prox-
imity constraint ensures that each image pixel belongs
to one and only one segmented region. To take the
proximity constraint into account, these methods em-
ploy extra terms based on the concept of region com-
petition, attempting to classify pixels on the region
boundaries only to the most probable regions they can
belong to.
In (Vese and Chan, 2002), the classic Chan-Vese
model is extended from object/background segmenta-
tion to multiple region segmentation. In this method,
different regions are binary coded by the signs of mul-
tiple level set functions so that the proximity con-
straint can be satisfied in an elegant and natural way.
In (Cremers et al., 2006), a quite different multi-
phase method was proposed, where auxiliary labeling
level set functions are introduced to dynamically di-
vide an image into multiple regions which are labeled
in a similar fashion as in (Vese and Chan, 2002) to
keep the proximity constraint. The uniqueness of the
method lies in that the labeled regions are not used
directly as the segmentation result but used to iden-
tify different regions so that different evolution rules
can be defined in differently labeled regions by using
a single “segmenting” level set function.
Based on the authors’ two earlier papers (Zhang
et al., 2008; Zhang and Matuszewski, 2009), we
propose a level-set based multiphase active contour
model dedicated to a different type of constraint —
the topology constraint. The model consists of two
major components. The first component, making use
of both boundary and regional information derived
from the input image, describes how each active con-
tour evolves independently. The second component
takes the interaction of multiple active contours into
account by using inter-object medial axes.
The rest of the paper is organized as follows. Sec-
tion 2 discusses the theory of the method. Section 3
shows results of applying the method on medical im-
ages, whereas the conclusions are drawn in Section 4.
2 THEORY
2.1 Hybrid Active Contour Model
First consider the case of a single active contour. Let
C denote an active contour and x denote a point in
the image domain Ω. Then, as illustrated in Fig-
ure 1, the level set function φ(x) can be defined to
have the following properties: (1) C = {x : φ(x) = 0};
(2) φ(x) > 0 for x inside the contour and φ(x) < 0
for x outside. The normal of the active contour
~
N is
defined as the unit direction expanding the contour.
~
N
−
~
N
C
φ(x) < 0
φ(x) > 0
Figure 1: An active contour and its level set function.
The proposed functional to be minimized can be
written as
E(φ(x)) = −
Z
Ω
P(I(x))H(φ(x))dx
+ α
Z
Ω
g(|∇I(x)|)|∇H(φ(x))|dx (1)
where: P(x) and g(x) are the regional and boundary
mapping functions related to the input image I(x),
H(x) represents the Heaviside function which has
value 1 when x ≥ 0 and 0 otherwise, and α is a scalar
factor used to balance the two terms. The first term of
the functional is the regional term, wherein the func-
tion P(x) is designed to map image intensities, ex-
pected to be typical for the object, to positive values
with all other image intensities being mapped to neg-
ative values. The selection of the regional mapping
function P(x) is image dependent but flexible. The
second term is the classical geodesic boundary term
as proposed in (Caselles et al., 1997). The bound-
ary mapping function g(x) is often chosen to be an
image edge indicator function which is a nonnegative
decreasing function of the image gradient.
By deriving the Gateaux derivative of the pro-
posed functional, the implicit PDE, describing the
evolution of active contour that minimizes the func-
tional, can be expressed as
A MULTIPHASE ACTIVE CONTOUR MODEL WITH DYNAMIC MEDIAL AXIS CONSTRAINT FOR MEDICAL
IMAGE SEGMENTATION
517

C
background
object
Figure 2: Regional term and its flow.
∂φ(x)
∂t
= P(I(x))|∇φ(x)|
+ α· ∇ ·

g(|∇I(x)|)
∇φ(x)
|∇φ(x)|

|∇φ(x)| (2)
The corresponding explicit PDE can be written as
∂C
∂t
= P(I(C)) ·
~
N
+α

g(|∇I(C)|)κ− < ∇g(|∇I(C)|),
~
N >

·
~
N (3)
with κ representing the curvature of C and < ·, · >
denotes the inner product of two vectors. A syn-
thetic P(x), where object pixels are mapped to 1 and
background pixels are mapped to -1, is shown in Fig-
ure 2 in order to illustrate the geometric interpretation
of the regional term. Superimposed on the image is
an active contour with arrows showing the motion of
the contour according to the regional term P(x)
~
N in
Equ. (3). It is clear that, in this case, the regional
term can always steer the active contour to the ob-
ject boundary (where the minimization of the regional
term in Equ. (1) is obtained) as long as the initial con-
tour has common interior area with the object. This
illustrates the robustness of the regional term which
can hardly be achieved by the boundary term alone
due to its narrow effective range and high sensitivity
to image noise. The value of the boundary term lies in
the fact that it can normally lead to more accurate seg-
mentation results when relatively strong boundaries
are presented in images. In case when boundary in-
formation is weak or ambiguous, the boundary map-
ping function can be chosen as g(x) = 1. Then the
boundary term in Equ. (3) is simplified to a curvature
flow term κ
~
N whose role is simply to smooth curve.
2.2 Multiphase Framework
In the proposed model, to jointly segment multi-
ple objects, multiple active contours, each associated
with a single object, need to be applied. If each active
contour evolves independently according to the evo-
lution rule in Equ. (3), a set of PDEs can be written
as
∂C
k
∂t
= V
k
(C
k
) ·
~
N, k = 1,...,n (4)
with n denoting the number of active contours and C
k
denoting the k
th
active contour. V
k
represents the ve-
locity along the normal direction of C
k
, which can be
written as
V
k
(x) = P
k
(I(x))
+α
k

g
k
(|∇I(x)|)κ− < ∇g
k
(|∇I(x)|),
~
N >

(5)
where the selections of P
k
(x), g
k
(x) and α
k
depend on
the corresponding object to be segmented.
In order to make active contours interact with
each other so that they can evolve in a more control-
lable way, a constraining component in the form of
D
k
(C
k
;C) is introduced into Equ. (4)
∂C
k
∂t
= V
k
(C
k
) ·
~
N + β
k
D
k
(C
k
;C) ·
~
N, k = 1,...,n
(6)
where C represent the entire set of active contours,
i.e, C = {C
1
,.. .C
n
}. In our study, medial axes are
found to be an elegant way to constrain the evolution
of multiple curves. The following two subsections de-
scribe how the medial axis can be related to the con-
straining component to impose topology and dynamic
shape constraints.
2.2.1 Topology Constraint
In medical images, topology of objects to be seg-
mented is often known and can be used as prior in-
formation. By using the prior, a set of initial contours
satisfying the topology can be established. The topol-
ogy constraint requires that the initial topology of the
contours should be preserved in the process of curve
evolution.
C
1
C
2
M
(a) Exclusion
C
1
C
2
M
(b) Inclusion
Figure 3: Two fundamental topological relationship studied
in this paper.
For any pair of curves, there are two fundamental
topological structures studied in this paper, namely,
exclusion and inclusion. The exclusion structure is il-
lustrated in Figure 3(a), where the two curves C
1
and
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
518

C
1
C
1
C
1
C
2
C
2
C
2
C
3
C
3
C
3
M
1
M
2
M
3
Figure 4: An example of topology of three curves and their
associated medial axes.
C
2
are disjoint, i.e., Ω
1
∩Ω
2
=
/
0 with Ω
k
denoting the
interior area ofC
k
throughout the paper. The inclusion
structure is illustrated in Figure 3(b), where one curve
contains the other, i.e., Ω
1
⊂ Ω
2
or Ω
2
⊂ Ω
1
. More
complicated topology can be built based on these two
fundamental structures. A example of three curve
configuration is shown in Figure 4. For the shown
configuration, the topological constraints can be writ-
ten as follows: Ω
1
∩ Ω
2
=
/
0, Ω
1
⊂ Ω
3
and Ω
2
⊂ Ω
3
.
For each evolving curveC
k
, a medial axis denoted
as M
k
is associated with it. The medial axis, depen-
dent on multiple curves, is defined as
M
k
(C) =

x : d(x;C
k
) = min
j6=k
d(x;C
j
)

(7)
with d(x;C) representing the Euclidean distance be-
tween the point x and the curve C. The medial axes
are shown as the dash curves in Figure 3 and Figure 4.
Note that the medial axes are identical if there are only
two curves. The details of an efficient way to calculate
medial axes can be found in (Zhang and Matuszewski,
2009).
A medial axis divides the image domain into two
regions — the region that only contains the associ-
ated active contour and the region that contains all
the other active contours. The topological structure
of multiple active contours is guaranteed to be pre-
served if none of the active contours ‘leak’ through
their corresponding medial axes to the other sides of
the regions. To prevent the leakage from happening,
forces induced from the medial axes can be exerted
on the corresponding active contours. Hence, the con-
straining term in Equ. (6) can be defined as
D
k
(x;C) = f
k
(sdf(x;M
k
(C))) (8)
where sdf(x;M
k
) represents the signed distance func-
tion which equals to d(x;M
k
) for the point x belong-
ing to the region that contains C
k
and −d(x;M
k
) oth-
erwise. f
k
(x) in Equ. (8) is the so-called distance-
to-force transfer function which maps the signed dis-
tance to medial axis to the force exerted on the as-
sociated active contour. An example of the transfer
function is f
k
(x) = x − γ with the positive distance
threshold γ, which indicates that the force exerted on
the associated active contour becomes more and more
repulsive (negative) as the active contour approaches
to its medial axis from its own side.
2.2.2 Dynamic Shape Constraint
Medial axis can also be used as a dynamic shape con-
straint for joint segmentation of multiple objects with
similar shapes in different images.
C
1
C
2
Figure 5: Basic idea of using medial axis as a dynamic
shape constraint.
The basic idea of dynamic shape constraint is il-
lustrated in Figure 5, where C
1
and C
2
are two active
contours taken from two different images and put into
the same figure for demonstration purpose. In this
case, the medial axis of the two curves, shown as the
dash curve in the figure, is defined as
M(C) = {x : d(x;C
1
) = d(x;C
2
) and x 6∈ Ω
1
∩ Ω
2
}
(9)
Consequently, the constraining term in Equ. (6) can
be defined as
D
k
(x;C) = sdf(x;M(C)) (10)
where sdf(x;M) represents the signed distance func-
tion that equals to d(x;M) for the point inside M and
−d(x;M
k
) otherwise. The medial axis can be consid-
ered as the mean shape of the two active contours and
it is dynamic in the sense that it also evolves as the ac-
tive contours evolve. The directions of the forces im-
posed on the active contours are indicated as arrows
in Figure 5. It can be seen that the forces tend to move
the contours towards their dynamic mean shape.
This approach can be easily extended to the case
of more than two curves as long as the mean shape of
multiple curves can be properly defined.
3 EXPERIMENTAL RESULTS
A couple of experiments on real medical images, us-
ing medial axis as topology constraint and dynamic
shape constraint respectively, are presented in this
section.
In the first experiment, the objective was to seg-
ment two ventriclesas well as the entire heart from the
MRI image of a mouse shown in the top-left image of
A MULTIPHASE ACTIVE CONTOUR MODEL WITH DYNAMIC MEDIAL AXIS CONSTRAINT FOR MEDICAL
IMAGE SEGMENTATION
519

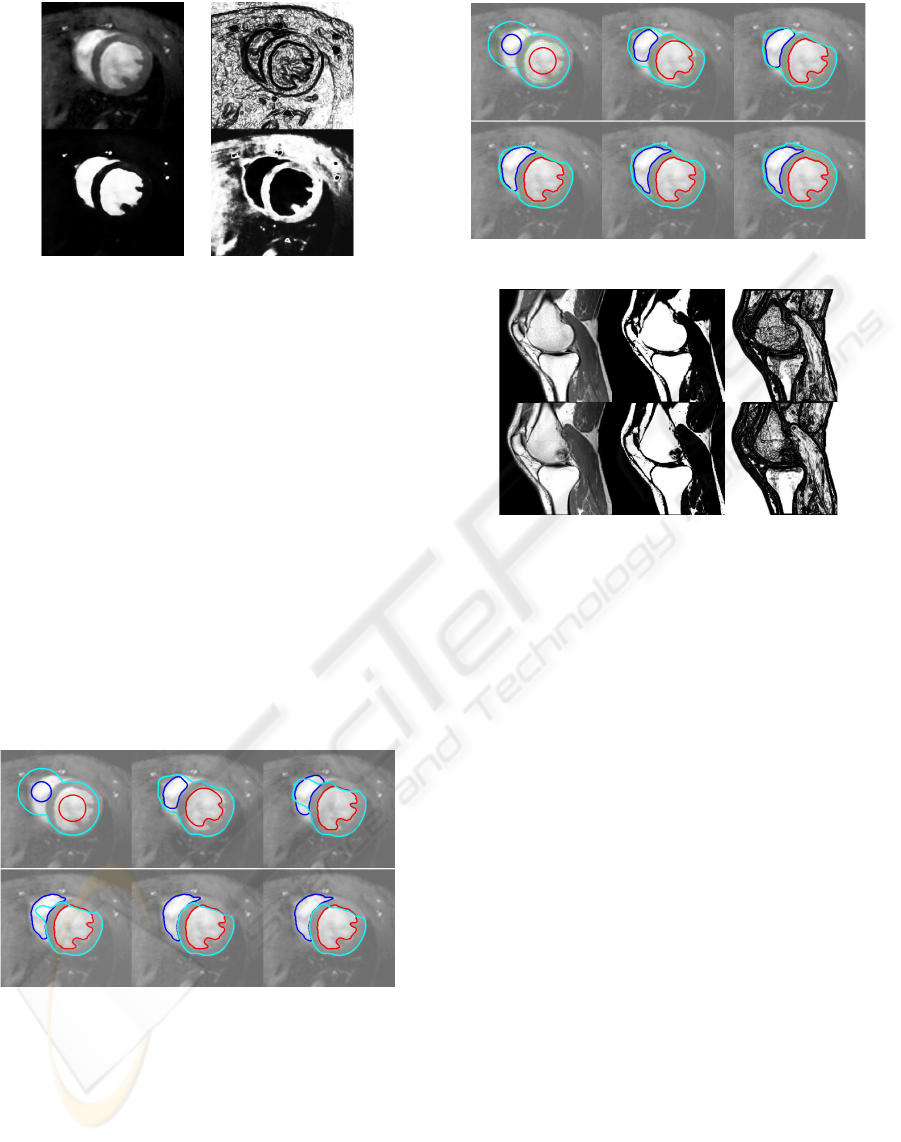
Figure 6: Original MRI image of mouse heart (left top); its
boundary term (right top) and regional terms (bottom). (Im-
age was kindly provided by the FUGE Molecular Imaging
Centre, Trondheim, Norway.)
Figure 6. The rest of the Figure shows the three im-
ages, obtained from the MRI image, encoding bound-
ary and regional terms (as g
k
and P
k
in Equ. (5)).
From the image slice, it can be seen that the objects to
be segmented have the same topological structure as
those in Figure 4, i.e., the heart includes both ventri-
cles and the ventricles are mutually exclusive. There-
fore three curves with the same topological structure
were initialized as shown in the first image of Fig-
ure 7. For comparison, curve evolution processes with
and without medial axis constraint are shown in Fig-
ure 7 and Figure 8 respectively. Curve evolution with-
out medial axis constraint clearly failed as the outer
contour collapsed, due to lack of well-defined infor-
mation of the outer heart wall, resulting in topological
changes.
iter. # 0 iter. # 5 iter. # 10
iter. # 15 iter. # 20 iter. # 30
Figure 7: Curve evolution without medial axis constraint.
In the second experiment, two knee images were
extracted from a volumetric MRI data. The objec-
tive was to segment bones from these images. The
original images as well as the processed images used
for regional and boundary terms are shown in Fig-
ure 9. Figure 10 shows the curve evolution when the
segmentation is performed independently. It can be
seen that the results for both images are not accept-
able — in the first image, leakage happened due to
weak boundary; in the second image, the resulting
iter. # 0 iter. # 5 iter. # 10
iter. # 15 iter. # 20 iter. # 30
Figure 8: Curve evolution with medial axis constraint.
Figure 9: First row: image 1; second row: image 2.
Columns from left to right: original image, regional term,
boundary term.
segmentation failed to include the lower right corner
of the upper bone due to dark shadow. As shown in
Figure 11, much better results were achieved by us-
ing the medial axis constraint with the two evolving
contours helping each other to converge to the correct
bone structures.
4 CONCLUSIONS
This paper proposes a multiphase active contour
method for simultaneous segmentation of multiple
objects in one or multiple images. In the method,
each object to be segmented is associated with an
active contour. The evolution PDE associated with
each active contour involves two main components —
the component responsible for analysis of the image
and each separate contour properties, and the com-
ponent encoding interaction between different evolv-
ing curves. For the former component, a model using
both boundary and regional information from input
images is proposed in order to achieve robust and ac-
curate results. In the model, medial axis plays an es-
sential role in composing the interaction components
to impose topology constraint or dynamic shape con-
straint to achieve robust results.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
520

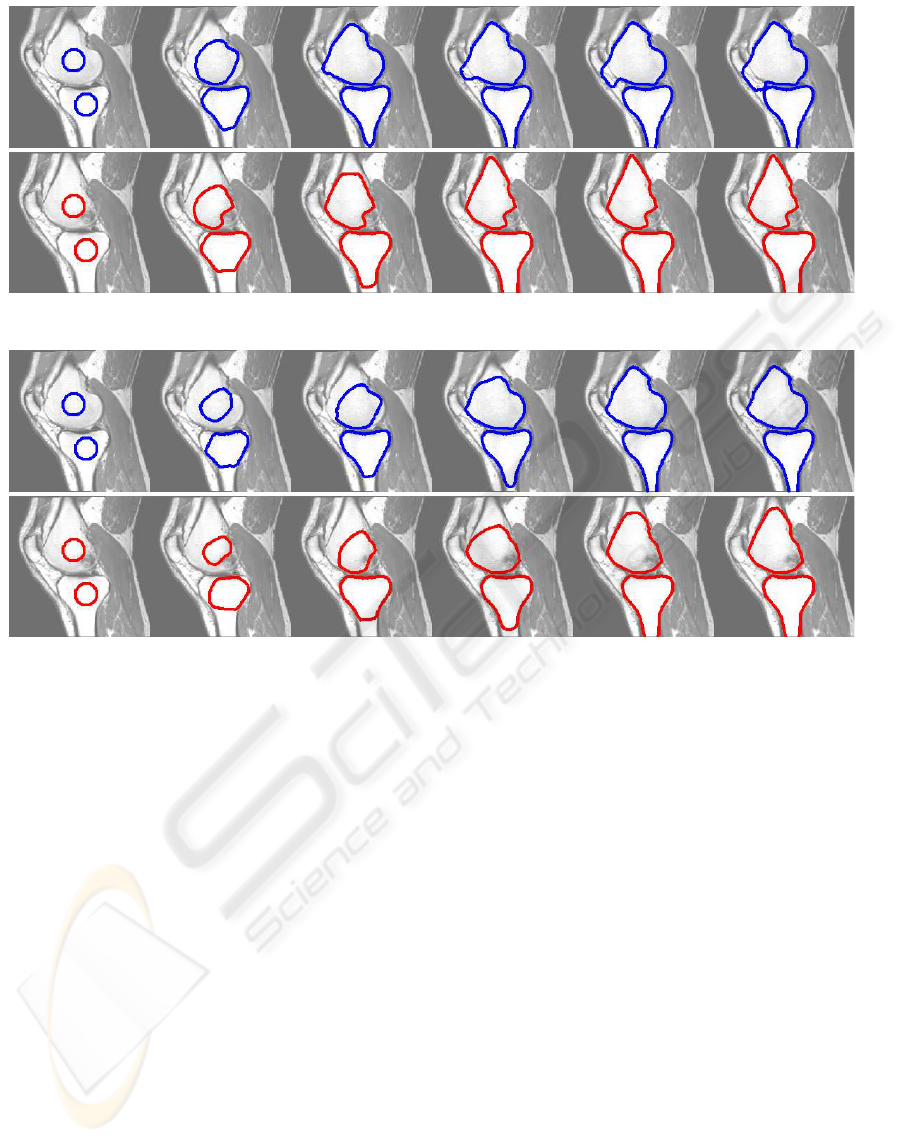
iter. # 0
iter. # 0
iter. # 10
iter. # 10
iter. # 20
iter. # 20
iter. # 30
iter. # 30
iter. # 40
iter. # 40
iter. # 50
iter. # 50
Figure 10: Curve evolution without medial axis constraint.
iter. # 0
iter. # 0
iter. # 10
iter. # 10
iter. # 20
iter. # 20
iter. # 30
iter. # 30
iter. # 40
iter. # 40
iter. # 50
iter. # 50
Figure 11: Curve evolution with medial axis constraint.
ACKNOWLEDGEMENTS
The work done in this paper has been supported
from the MEGURATH project (EPSRC project No.
EP/D077540/1).
REFERENCES
Brox, T. and Weickert, J. (2006). Level set segmentation
with multiple regions. IP, 15(10):3213–3218.
Caselles, V., Kimmel, R., and Sapiro, G. (1997). Geodesic
active contours. IJCV, 22:61–79.
Chan, T. F. and Vese, L. A. (2001). Active contours without
edges. IP, 10(10):266–277.
Cremers, D., Schen, N., and Schnrr, C. (2006). A
multiphase dynamic labeling model for variational
recognition-driven image segmentation. IJCV, 66:67–
81.
Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:
Active contour mdoels. IJCV, 1:321–331.
Lankton, S. and Tannenbaum, A. (2008). Localizing region-
based active contours. IP, 17(11):2029–2039.
Malladi, R., Sethian, J., and Vemuri, B. (1995). Shape mod-
eling with front propagation: A level set approach.
PAMI, 17:158175.
Precioso, F., Barlaud, M., Blu, T., and Unser, M. (2005).
Robust real-time segmentation of images and videos
using a smooth-spline snake-based algorithm. IP,
14(7):910–924.
Vese, L. A. and Chan, T. F. (2002). A multiphase level set
framework for image segmentation using the mum-
ford and shah model. IP, 50(3):271–293.
Zhang, Y. and Matuszewski, B. J. (2009). Multiphase active
contour segmentation constrained by evolving medial
axes. In ICIP’09, IEEE 16th International Conference
on Image Processing. IEEE Press.
Zhang, Y., Matuszewski, B. J., Shark, L.-K., and Moore,
C. (2008). Medical image segmentation using new
hybrid level-set method. In MediVis’08, 5th Inter-
national Conference BioMedical Visualization: Infor-
mation Visualization in Medical and Biomedical In-
formatics. IEEE Press.
A MULTIPHASE ACTIVE CONTOUR MODEL WITH DYNAMIC MEDIAL AXIS CONSTRAINT FOR MEDICAL
IMAGE SEGMENTATION
521