
On the Construction of Gestalt-Algebra Instances and a
Measure for their Similarity
Eckart Michaelsen
Fraunhofer IOSB, Gutleuthausstrasse 1, 76275 Ettlingen, Germany
Abstract. Four construction principles that compose more complicated percep-
tual gestalts from less complex ones are defined in detail: Mirror gestalts, lat-
tice gestalts, rotational mandalas, and clusters, respectively. These can be en-
capsulated as constructions in a production system. Since any of the four con-
structions can work on any gestalt, a recursive and very expressive scheme is
set up with many prospective applications in image mining. Of particular inter-
est is such analysis for aerial and satellite images and for façade images of
buildings.
1 Introduction
Gestalt is ubiquitous in nature as well as in man-made artifacts. Recognition of gestalt
goes far beyond today’s understanding of “pattern recognition”. We have to drop
back to a naïve understanding of the word “pattern”, to forget the feature vectors we
are used to deal with in the pattern recognition community and imagine patterns we
perceived occasionally in a more contemplative situation. Usually we are not aware of
the mathematics, particularly of the implicit algebra in our intuitive understanding of
gestalt, like symmetries, repetition, rotational mandalas, variation, etc. Understanding
the word “recognition” according to its Latin roots means to reconstruct the hidden
gestalt idea, resulting, as far as possible, in the most probable explanation. The
appearance of a gestalt is uncertain – there may be displacement, deletion and clutter.
Humans still recognize the gestalt. For a machine, however, this poses a very hard
search task which nonetheless is indispensible for real content-based image mining.
1.1 Related Work
For more than thirty years now automatic analysis of complex aerial images has been
a challenge and also basic approaches to their algebraic gestalt have been attempted
[11]. Today emphasis is more on learning of rules and stochastic modeling of con-
straints and relations [12]. Automatic understanding of buildings currently also in-
cludes façade analysis [17] including the grouping of semantically similar SIFT in-
stances in lattices [13]. The main economic motive is apparently application in the
games industry. The computer graphics community acknowledged that a deeper un-
derstanding of gestalt principles and design customs in architecture are prerequisite to
Michaelsen E. (2010).
On the Construction of Gestalt-Algebra Instances and a Measure for their Similarity.
In Proceedings of the Third International Workshop on Image Mining Theory and Applications, pages 51-59
DOI: 10.5220/0002962400510059
Copyright
c
SciTePress

swift setup and detailed elaboration of cyber city models [16]. This includes work for
archeologists as well. Up to now we are not aware of much other work on gestalt
recognition in our understanding in the machine vision community. This paper con-
tinues work presented in [8, 10]. Here we focus on the precise construction methods.
2 Constructions of Gestalts
Given a set of points and corresponding assignments to orbits a new gestalt instance
is constructed by error sum minimization. The errors are displacements between the
actual positions of the points and the set positions given by the gestalt principle and
the corresponding attribute values. All gestalts are given modulo the action of a par-
ticular group on the indices of the points, which do not alter the identity of an in-
stance. We distinguish the following constructions:
2.1 Mirror Symmetry Gestalt
Given k pairs (p
1,0
, p
1,1
), …, (p
k,0
,p
k,1
) of points in the usual 2D vector space, we are
looking for an optimal axis a such that by a mirror mapping according to this axis the
points p
i,j
are flipped into the points p
i,j+1
in the least squares error manner. Here we
have i=1…k, and j=0,1 to be understood modulo 2. We can decompose the constraint
into two parts: 1) The axis should be incident with the k midpoints (p
i,0
+p
i,1
)/2. And
2) the axis should be perpendicular to the k difference vectors p
i,0
-p
i,1
. This leads to a
linear one-step solution using singular value decomposition of the matrix
1,01,1 1,01,1
,0 ,1 ,0 ,1
1, 0 1,1 1, 0 1,1
,0 ,1 ,0 ,1
2
2
0
0
xx yy
xxyy
kkkk
yy xx
yyxx
kkkk
pp pp
pppp
pp pp
pppp
(1)
(upper indices x and y indicate the coordinates in 2D). The eigenspace corresponding
to the least singular value is accepted as solution a (axis equation for the new gestalt).
Furthermore the new gestalt obtains the center of gravity of all points as position o.
We state here without proof that this algebraic solution approaches the desired least
squares solution – for which according to its non-linear setting an iterative calculation
would be necessary – provided that the coordinate system is chosen properly. For our
preference towards one-step linear algebraic solutions we refer to [4]. Figure 1 dis-
plays such minimization and the histogram of residuals. We have used particular such
gestalt instances in SAR-image understanding [9]. It is evident that this definition is
invariant under action of the trivial finite group of order 2 on the second index 0↔1.
The gestalt is understood modulo this group.
52
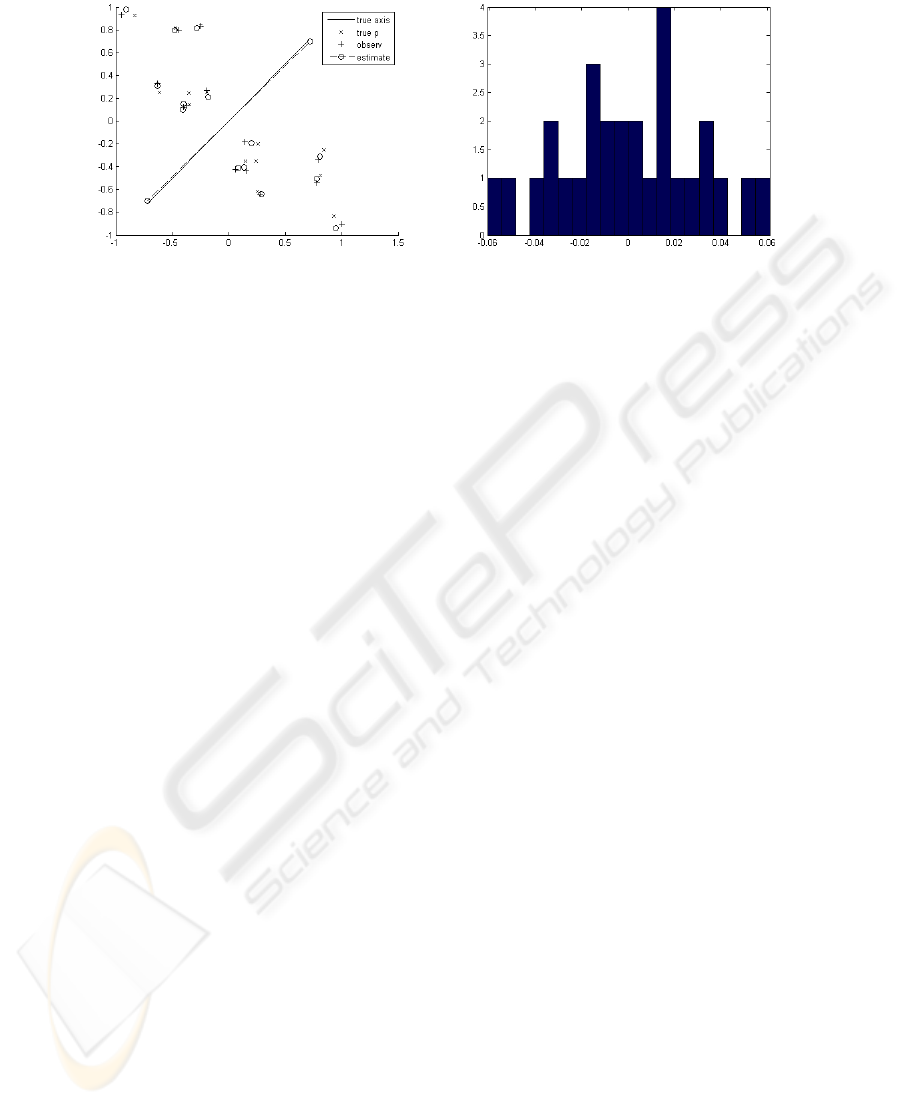
Fig. 1. Left: Construction of a mirror symmetry gestalt– here with k=7 point pairs and σ=0.07;
right: Histogram of the residuals.
2.2 Lattice Gestalt
Given k m-tuples (p
1,0
, …,p
1,m-1
), …, (p
k,0
, …, p
k,m-1
) of points, we are looking for an
optimal common start position p
o
and a shift vector v such that:
2
1
,,
10
()
km
io ij
ij
jpvp
(2)
This is a linear problem and thus the one-step linear algebraic solution is indeed
the least squared error sum solution. It is just averaging the differences for v and
taking the center of gravity for o is optimal. The construction of the starting points
p
,i,o
is also trivial. A typical lattice gestalt is depicted below in Figure 3.
2.3 Rotational Gestalts
Given k m-tuples (p
1,0
, …,p
1,m-1
), …, (p
k,0
, …, p
k,m-1
) of points, we are looking for an
optimal common center point o such that by rotation with angle 2π/m the points p
i,j
are mapped onto the points p
i,j+1
in the least squares error manner. Here we have
i=1…k, j=0…m-1. This leads to a sum of squared errors reading
2
1
2/ , ,
10
()()
km
jkio ij
ij
Mpopo
(3)
to minimized, where o and the vectors p
i,o
are varying. M
α
denotes the usual turning
matrix for angle α in 2D. Already from this definition can be seen that the gestalt has
to be understood modulo the finite rotation group of order m. I.e. a cyclic shift on the
indices j does not change the identity of the gestalt. The vector p
i,o
that results from
the minimization has to be understood as giving a radius for the ith orbit with its
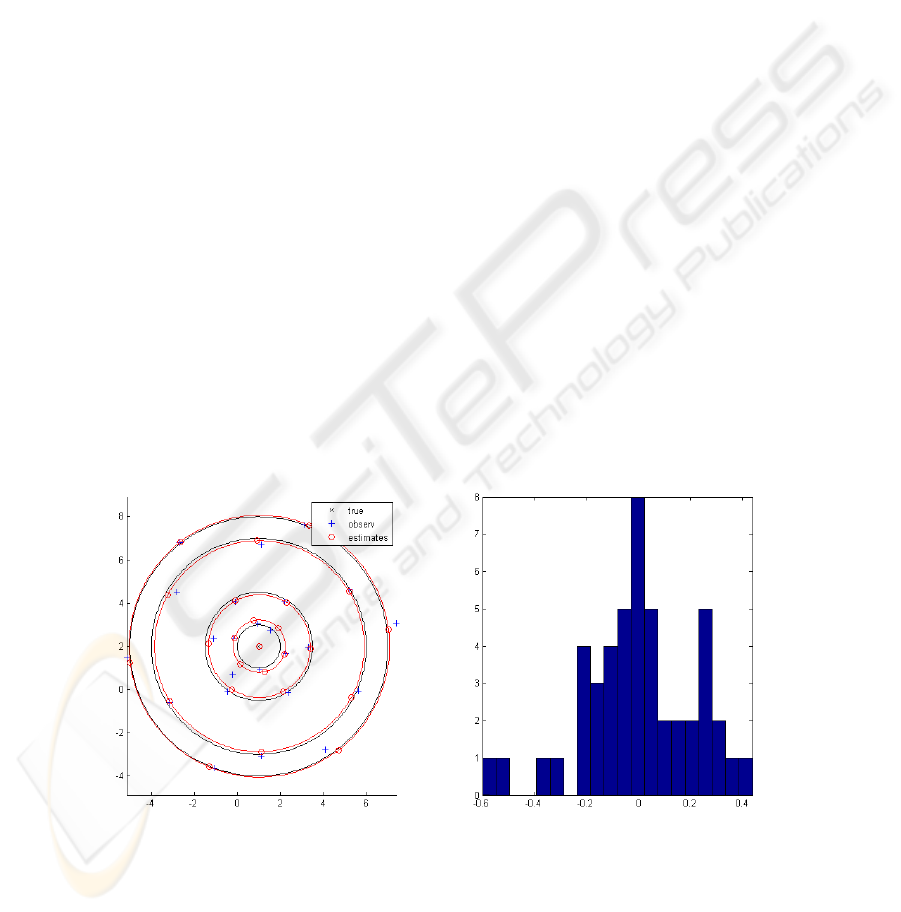
length and a phase modulo 2π/m. Figure 2 shows the situation. Minimization of (3) is
a non-linear problem closely related to circle fitting.
53
We are not aware of a direct linear algebraic setting for it (such as is presented for
mirror gestalts above). We refer to the closely related circle fitting problem [6], and
initialize o by the center of gravity of all observed points and p
i,o
by p
i,0
. The itera-
tion is performed using the Jacobian displayed in (4). Entries to the matrix are the
partial derivatives ρ for the current iteration. As above the lower indices denote i (the
index inside the orbit), and j (the index of the orbit) respectively. Upper index x or y
denotes the direction in the plane. The parameter vectors p
i,o
are treated with radius r
and phase p. These are the other upper indices.
1,0 1,0
10
1, 1 1, 1
10
00
01
10 10
01
1, 1 1, 1
00
10
,0 ,0
10
,1 ,1
00
01
00
01
,1 ,1
rx px
rx px
mm
ry py
ry py
mm
rx px
kk
rx px
km km
ry py
kk
ry py
km km
(4)
The columns of this matrix correspond to the parameters o
x
, o
y
, r
1
, p
1
, …, r
k
, p
k
and the rows to the current residuals. For iteration this matrix has to be squared and
inverted in each step. For the rotational gestalt we observed that convergence is
quick. Usually three or four steps are sufficient.
Fig. 2. Left: Construction of a rotational symmetry – here of order m=6 with k=4 orbits and
σ=0.25; right: Histogram of the residuals.
54

2.4 Cluster Gestalts
A very important principle in gestalt perception is proximity. This clusters a set of
adjacent points into a new gestalt by constructing the center of gravity as new posi-
tion o. Also the eigenspace corresponding to the larger eigenvector may be used as
orientation attribute v. Clustering also yields a sum of squared residuals. The parts are
added to the cluster gestalt as set – i.e. the full permutation group acting on the indic-
es of the parts does not alter identity of the cluster gestalt instance. Clusters are the
least significant gestalt. If any of the gestalt constructions listed above applies better,
they will be preferred.
3 Testing for Equality and Similarity
When entering a newly constructed gestalt instance into the database care has to be
taken that this gestalt has not yet been constructed in a different order or manner.
Actually, this is the part where algebraic knowledge is required most of all. In fact,
almost for any gestalt construction trees there are very many other possible construc-
tions. The same object may be described in different ways. Here we need canonic
representatives allowing swift tests for equality – and more important: A metric or
similarity measure that does not require extensive computational effort. For gestalts
with uncertainty care has to be taken, that all construction principles use the same
kind of residuals – here squared error sums – so as to compare two different descrip-
tions for the same set of primitives and decide for the simplest description with mi-
nimal squared error sum.
3.1 Sub-lattices and Lattices of Lattice Gestalts
Any lattice of size m can also be understood as lattice using -v as translation vector
and replacing j by m+1-j. Moreover, if m is not a prime number and thus can be de-
composed m=pq a lattice gestalt of order m can also be understood as lattice of size p
containing sub-lattices of size q (and vice versa). According to the Helmholtz prin-
ciple of the “maximal meaningful element” as claimed by A. Desolneux [3] the max-
imal gestalt is the preferred canonic description, in which the gestalt is to be stored in
the database. Particular lattice gestalts – of bright spots, i.e. salient scatterers - have
been investigated in [9] as well. This includes the preference for maximal gestalts
(scatterer rows).
Occasionally, we have coded a production system grouping rows of rows where
the outer gestalt has a different direction than the inner ones (preferably perpendicu-
lar) [15]. This can be seen as a practical step towards gestalt algebra. Columns of
objects which form again a row are one of the main examples, ubiquitous in facades
and remotely sensed industrial sites. Again, the situation is different with angle be-
tween the inner and the outer vector: Vectors of π/3, π/4 or π/6 difference in orienta-
tion and of equal length construct a 2D-lattice (triangular, orthogonal or hexagonal).
There is an elaborated theory on these wallpaper lattices [5] and also practical work
55
of recognition of such lattices [1]. We also refer to the investigations on 2D and 3D
lattices going on in Physics [14] and in particular in cristallography. In aerial images
or images of facades, in particular, orthogonal 2D lattices are not rare. However, we
do not introduce these as a special gestalt. Instead, the equality test has to take care of
the different possibilities. If the angle is not very close to one of the three wallpaper
possibilities, or if the length of the vectors v is different there will be a preferable
canonic representation: The classical gestalt principle proximity demands that the
closer objects are grouped first into the inner lattice, after that these columns are
grouped into rows – with longer distance vector v. Moreover, we are not treating
infinite lattices here.
3.2 Sub-rotations of Rotational Gestalts
In analogy to the lattice gestalts we have to take care here also whether m is a prime
number. If not it can be decomposed m=pq and the rotational gestalt can also be un-
derstood as rotational gestalt of order p or also q (in accordance to the decomposition
of the finite cyclic groups of order m). Again obeying the Helmholtz principle the
maximal gestalt is the preferred canonic description, in which the gestalt is to be
stored in the database, provided it yields no significantly larger error sum.
3.3 Equality of Lattice and Mirror Gestalts
It is easily verified that a lattice of symmetric gestalts can also be understood as mir-
ror symmetry provided that the symmetry axes of the parts a
i
are perpendicular to the
generating vector v. For an even m there will be k·m/2 mirror orbits created by flip-
ping i,j↔m-i,j and simultaneously switching the internal mirror indices. Figure 3
shows such a case. According to gestalt principles the simplest model is again pre-
ferred as canonic description – which is here of course the lattice.
Fig. 3. A lattice with m=5 and k=4 orbits (traces); it can also be understood as mirror gestalt
with the axis displayed dotted.
3.4 Equality of Rotational and Mirror Gestalt
Provided that the axes of symmetric parts of a rotational gestalt all are incident with
the center of this rotational gestalt it can also be understood as a symmetry gestalt
56

with respect to any of axes of its parts. Here we have to change the rotation direction
of the indices in the orbits and also flip the internal mirror indices around. Rotational
symmetry is regarded as stronger than mirror symmetry. Thus such a gestalt will be
stored as rotation in the database, provided it yields no significantly larger error sum
4 Coding the Search for Gestalts as Production System
Searching for gestalt instances in measured image data using the algebraic structures
outlined above poses a non-trivial challenge. We recommend using the production
system interpreter as outlined e.g. in [9]. It has any-time performance, avoids com-
plete search, is quality driven bottom-up per default and allows sophisticated top-
down acceleration. The class Gestalt is inherited from the class CImageObject and
may thus be handled by this interpreter. All other classes listed in Table 1 below are
in turn inherited from the class Gestalt.
Table 1. Productions coding the gestalt constructions above.
Right side
comment construction Left side
MirrorGestalt ← only 2 instances Sect. 2.1 Gestalt, Gestalt
LatticeGestalt ← starting a row Sect. 2.2 Gestalt, Gestalt
LatticeGestalt ← continuing “ LatticeGestalt, Gestalt
RotatGestalt ← starting a row Sect. 2.3 Gestalt, Gestalt
RotatGestalt ← cont. until full “ RotatGestalt, Gestalt
ClusterGestalt ← Sect. 2.4 Gestalt, …, Gestalt
Productions for this interpreter usually have not only a construction function for
the right hand side but also a condition on the left hand side objects in order to avoid
any object to be combined with any other (constrained set grammar). This is omitted
here, because our approach attempts to construct a gestalt algebra – where indeed any
member should be a possible partner for any other member. In practice, however, a
threshold should be set on the residual error sum (which of course sets the quality
assessment driving the search). The constraint resulting from such a threshold can be
transformed into a search region setting a focus where to look for prospective partner
gestalts.
The productions listed in the table can construct arbitrarily complex gestalt alge-
bra instances such as sketched in [10]. First parts of this coding endeavor have al-
ready been accomplished. But there remain some questions which have to be ans-
wered before the whole system can be set up. These are discussed below.
5 Discussion and Conclusions
This contribution introduced in more detail the constructions necessary for setting up
gestalt algebra as indicated earlier in [8, 10]. It is our goal to add more precision and
detail on the way to the implementation of this structure for practical applications.
57

As long as the set of equality and similarity relations and canonical forms for ges-
talts, as listed in chapter 3, is not complete there is little sense in starting the coding
endeavor. While for infinite 2D lattices there is an elaborated mathematical theory at
hand for more than hundred years [2], we have no proof for completeness of the list
of Section 3 indicating possible different appearances of the same finite gestalt with
respect to all our gestalt constructions yet.
As indicated in Section 3 in the description of a composed gestalt simplicity in the
tree structure (flatness of hierarchy) has to be balanced against the achieved squared
residual sum. Another open problem concerns the scale: Gestalt instances with a deep
tree composed from many objects distributed on a large area should be assessed on a
different scale. But the common displacement error measure is a prerequisite of mu-
tual comparison for the gestalts. We are looking forward to interesting future work.
References
1. Agusti-Melchor, M., Valiente-Gonzalez, J.-M., Rodas-Jorda, A.: Lattice Extraction Based
on Symmetry Analysis. VISAPP 2008, INSTIC, Portugal, ISBN: 978-989-8111-21-0
(2008) 396-402
2. Bravais, A., "Mémoire sur les systèmes formés par les points distribués régulièrement sur
un plan ou dans l'espace", J. Ecole Polytech. Vol. 19 (1850) 1–128
3. Desolneux A., Moisan L., Morel J.-M.: From Gestalt Theory to Image Analysis. Springer,
Berlin (2008)
4. Hartley, R., Zisserman, A.: Multiple View Geometry. Cambridge Unv. Press, sec. edition
(2003)
5. Horne, C. E.: Geometric symmetry in patterns and tilings. Woodhead Publishing. Abington
Hall, England, ISBN 1 85573 492 3 (2000)
6. W. Gander, G. H. Golub, R. Strebel: Least Squares Fitting of Circles and Ellipses. BIT
Numerical Mathematics, Springer Netherlands, Volume 34, Number 4 / Dezember (1994)
7. van Leeuwen, J. (ed.): Computer Science Today. Recent Trends and Developments. Lec-
ture Notes in Computer Science, Vol. 1000. Springer-Verlag, Berlin Heidelberg New York
(1995)
8. Michaelsen, E., Meidow, J.: Basic Definitions and Operations for Gestalt Algebra. In:
Gurevich, I., Niemann, H., Salvetti, O. (eds.) Image Mining Theory and Applications. In-
stic Press, Portugal, ISBN 978-989-8111-42-5 (2009) 53-62.
9. Michaelsen, E., Stilla, U., Soergel, U., Doktorski L.: Extraction of building polygons from
SAR images: Grouping and decision-level in the GESTALT system. Pattern Recognition
Letters, to appear 2010, online under http://dx.doi.org/10.1016/j.patrec.2009.10.004 (2009)
10. Michaelsen, E., Arens, M., Doktorski, L.: Elements of a Gestalt Algebra: Steps Towards
Understanding Images and Scenes. In: Gurevich, I., Niemann, H., Salvetti, O. (eds.): Image
Mining Theory and Applications. Instic Press, Portugal, ISBN 978-898-8111-25-8 (2008)
65-73.
11. Nagao, M., Matsuyama, T.: A Structural Analysis of Complex Aerial Photographs. Plenum
Press, New York London (1980)
12. Porway, J., Wang, Q., Zhu, S. C.: A Hierarchical and Contextual Model for Aerial Image
Parsing. Int. J. Comput. Vis. DOI 10.1007/s11263-009-0306-1, online at Springerlink.com,
(2009)
13. Priese, L., Schmitt, F., Hering, N. (2009): Grouping of Semantically Similar Image Posi-
tions. In: Salberg, A-B., Hardeberg, J. Y., Jenssen, R. (eds.): SCIA 2009, Oslo, Norway,
58

June 15-18, Proceedings. Bd. 5575. (2009) 726--734
14. Sternberg, S.: Group Theory and Physics. Cambridge University Press (1995)
15. Stilla, U., Michaelsen, E., Soergel, U., Schulz K.: Perceptual Grouping of Regular Struc-
tures for Automatic Detection of Man-Made Objects Examples from IR and SAR. IGARS
2003, IEEE, 0-7803-7930-6, (2003)
16. Watson, B., Wonka, P. (Guest editors): Perceptual Methods for Urban Modeling. IEEE
Computer Graphics, Vol. 28, No. 3 (May/June 2008)
17. The e-TRIMS project. http://www.ipb.uni-bonn.de/projects/etrims/ (last accessed Februar
2010)
59
