
A STUDY ON ALIGNING DOCUMENTS USING THE CIRCLE OF
INTEREST TECHNIQUE
Daniel Joseph and C´esar A. Mar´ın
Centre for Service Research, The University of Manchester, Booth Street West, Manchester M15 6PB, U.K.
Keywords:
Document alignment, Circle of interest, Formal concept analysis, Rough set theory, Semantic alignment.
Abstract:
In this paper we present a study on applying a technique called Circle of Interest, along with Formal Concept
Analysis and Rough Set Theory to semantically align documents such as those found in a business domain.
Indeed, when companies try to engage in business it becomes crucial to keep the semantics when exchanging
information usually known as a business document. Typical approaches are not practical or require a high cost
to implement. In contrast, we consider the concepts and their relationships discovered within an exchanged
business document to find automatically an alignment to a local interpretation known as a document type.
We present experimental results on applying Formal Concept Analysis as the ontological representation of
documents, the Circle of Interest for selecting the most relevant document types to choose from, and Rough
Set Theory for discerning among them. The results on a set of business documents show the feasibility of our
approach and its direct application to a business domain.
1 INTRODUCTION
The lack of a semantic alignment drives companies to
misinterpret any exchanged information known as a
business document (cf. a purchase order) when trying
to collaborate. This is due to the individual focus of
each company on different pieces of information lea-
ding to missing important data or having extra non-
relevant data.
Typical approaches address this issue by 1) ali-
gning ontologies (Chalupsky, 2000); 2) merging dif-
ferent ontologies (Dou et al., 2006); or 3) creating
standards meant for all companies to adopt (OASIS,
2001). However, they convey to troublesome situa-
tions such as agreeing on a common ontology re-
presentation in advance, creating specialised mapping
rules, and incurring in high cost for standardising in-
ternal information, respectively. In essence, these so-
lutions are costly and impractical especially for me-
dium and small companies that frequently exchange
business documents.
In this paper we present a study on the applica-
tion of a technique called Circle of Interest, along
with Formal Concept Analysis (FCA) and Rough
Set Theory (RST) for document alignment. We use
the discovered ontology within a business document
(simply named document hereafter) to align it to a lo-
cal abstraction of information called document type.
Our choice of semantic descriptors for discovered
concepts within a document maintains both the rela-
tions between concepts and the semantic structure of
the document.
We show experimental results on using FCA as
the ontology representation, the Circle of Interest for
creating the pool of the most relevant document types
to choose from, and RST for determining the appro-
priate one. Moreover, our results demonstrate the
feasibility of such a combination of techniques and
its applicability to document alignment in a practi-
cal business domain. This work has been carried
out within the scope of the EC-funded project Com-
mius (Community-based Interoperability Utility for
SMEs.)
The remaining of the paper is structured as fol-
lows: Section 2 provides the backgrounddetails about
FCA, RST and our choice for document descriptors.
Then Section 3 introduces the relevant definitions to
the document alignment process and the Circle of In-
terest technique. The experimental results are descri-
bed in Section 4 followed by a discussion and a lite-
rature review in Sections 5 and 6 respectively, before
summarising and concluding in Section 7.
374
Joseph D. and A. Marín C. (2010).
A STUDY ON ALIGNING DOCUMENTS USING THE CIRCLE OF INTEREST TECHNIQUE.
In Proceedings of the 5th International Conference on Software and Data Technologies, pages 374-383
DOI: 10.5220/0002965003740383
Copyright
c
SciTePress
2 PRELIMINARIES
2.1 Formal Concept Analysis (FCA)
FCA is a mathematical theory developed in the early
1980s (Wille, 2005) mainly used for analysing data,
representing knowledge, and managing information
by identifying conceptual structures within data sets
(Priss, 2006), cf. an ontology. We briefly present its
definitions.
Definition 1 (Formal Context (Wille, 2005)). It is
defined as a triple K := (G, M, I) where G is a set
of objects, M is a set of attributes, and I ⊆ G × M
is the set of binary relations between the elements of
the two.
Definition 2 (Formal Concept (Wille, 2005)). It is
defined within the context K as a pair (A, B) such that
A = B
⊳
and B = A
⊲
, where for A ⊆ G, A
⊲
is defined
as {m ∈ M | ∀g ∈ A : (g, m) ∈ I}, i.e. A
⊲
is the set of
attributes that all objects in A possess. For B ⊆ M,
B
⊳
is defined as {g ∈ G | ∀m ∈ B : (g, m) ∈ I}, i.e.
B
⊳
represents the set of objects that possess all the
attributes in B. For a formal concept (A, B), A and B
are called the extent and the intent respectively.
Definition 3 (The Sub Concept - Super Concept
Relation (Wille, 2005)). It is a partial order repre-
sented as (A
1
, B
1
) ≤ (A
2
, B
2
) :⇐⇒ A
1
⊆ A
2
(⇐⇒ B
1
⊇
B
2
), i.e. the concept (A
1
, B
1
) is a sub concept of (A
2
,
B
2
) if all the objects in A
1
are also contained in A
2
which is equivalent to have all the attributes in B
2
also
in B
1
. The same relation representation allows us to
call (A
2
, B
2
) a super concept of (A
1
, B
1
).
Definition 4 (Concept Lattice (Wille, 2005)). A
concept lattice of a given context K is that complete
lattice formed by the set of all formal concepts in
I for which a sub concept - super concept relation
is maintained. That is, for any given set of formal
concepts { (A
i
, B
i
) | i ∈ I} the supremum is the least
super concept of all the concepts in the set. Like-
wise, the infimum is the greatest sub concept of all
the concepts in the set. However, neither the supre-
mum nor the infimum is necessarily within the set.
A formal context K can be represented by a table
where the objects are shown in the first column and
the attributes in the first row. A cross ’X’ indicates
the binary relation between an object and an attribute
in the appropriate cell.
For example, Table 1 depicts a formal contextwith
five objects and four attributes. Let us say we want to
identify a formal concept containing DOC 1. We find
out that DOC 2 also contains the same attributes as
DOC 1 ({cc-b, cc-d}). Thus, we say that A = {DOC
1, DOC 2} is the set of objects we are interested in
Table 1: A formal context K.
cc-a cc-b cc-d cc-d
DOC 1 X X
DOC 2 X X
DOC 3 X X
DOC 4 X X X
DOC 5 X X X
and B = {cc-b, cc-d} is the set of attributes contained
by the objects in A, i.e. B is the intent and A is the
extent of the formal concept (A, B).
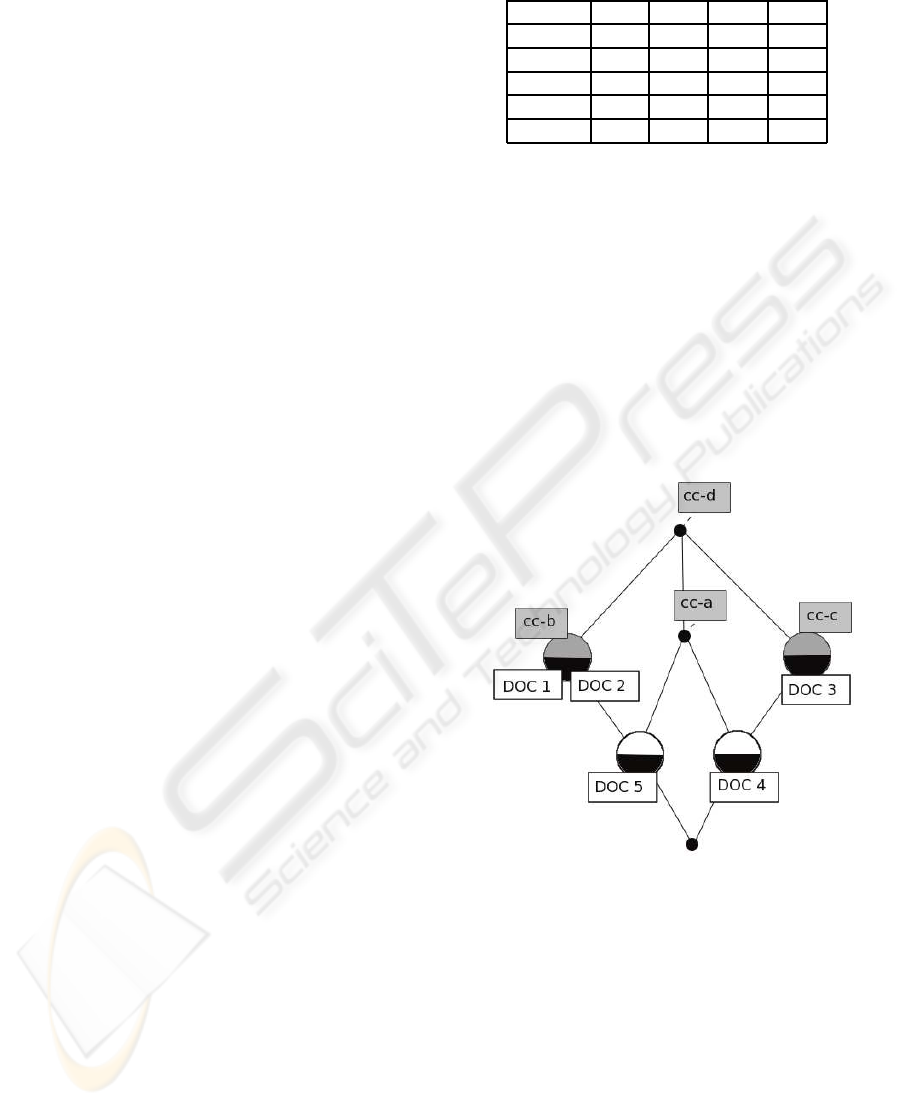
A concept lattice of the formal contextrepresented
by Table 1 is illustrated by Figure 1, in which a formal
concept is a node in the lattice whose intent are the
attributes in the direct path all the way up the lattice.
Its extent are the objects (DOC) found in the direct
path all the way down the lattice.
For instance in the same figure, the node contai-
ning {DOC 1, DOC 2} has the attribute set {cc-b, cc-
d} as the intent, and the object set {DOC 1, DOC 2,
DOC 5} as the extent.
Figure 1: A concept lattice of K.
2.2 Rough Set Theory (RST)
RST is a mathematical approach to deal with vague-
ness, uncertainty, and imprecision (Pawlak, 1982). It
replaces a “vague concept” by two “precise concepts”
named the lower and upper approximations. The
former contains those elements that are definitely
members of the “vague concept”, whereas the lat-
ter contains those elements that might belong to the
concept.
Definition 5 (The Indiscernible Relation (Zdzislaw,
1997)). Let U be a finite set of objects (cf. concept
set G in FCA), C be a finite set of attributes (cf. M
A STUDY ON ALIGNING DOCUMENTS USING THE CIRCLE OF INTEREST TECHNIQUE
375

in FCA), and for each c ∈ C a set of its values V
c
is
associated. Every attribute c determines a function
f
c
: U → V
c
. Then every subset of attributes B ⊆ C
has an associated indiscernible relation on U defi-
ned as I(B) = {(x, y) ∈ U × U : f
b
(x) = f
b
(y), ∀b ∈
B}. If (x, y) belongs to I(B) it is said that x and
y are B-indiscernible. Moreover, B(x) ⊆ U repre-
sents an equivalence class of x where x and y are B-
indiscernible. Notice that x ∈ B(x) since (x, x) is a
valid relation in I(B).
Table 2 represents a universe (cf. a context) in
which DOC 2 and DOC 3 are B-indiscernible with
respect to the attribute set {cc-a, cc-b, cc-c} as they
have the same attribute values. If we consider the
attribute set B = {cc-b, cc-c} then the equivalence
classes would be {DOC 1, DOC 2, DOC 3}, {DOC
4}, and {DOC 5, DOC 6}. Finally, an equivalence
class to DOC 5 would be B(DOC5) = {DOC 5, DOC
6} using B = {cc-b, cc-c} as the attribute set.
Table 2: A formal context with arbitrary concepts.
cc-a cc-b cc-c
DOC 1 X X
DOC 2 X
DOC 3 X
DOC 4
DOC 5 X
DOC 6 X X
Definition 6 (Lower and Upper Approximations
(Zdzislaw, 1997)). Let X be a subset (cf. a concept)
of the universe U and B be a subset of attributes C.
Then the following two sets are assigned to every sub-
set X
B
∗
(X) = {x ∈ U : B(x) ⊆ X} (1)
B
∗
(X) = {x ∈ U : B(x) ∩ X 6=
/
0}. (2)
Such sets are called B-lower and B-upper approxima-
tions of X respectively, where the former is the equi-
valence class of x actually existing within X, and the
latter represents the elements of the equivalence class
of x that could be in X.
RST gives us the ability to determine to what de-
gree an object is an element of a particular rough
set. To determine the similarity, (Zdzislaw, 1997)
defines a rough membership function giving an alge-
braic method to determine the numeric value of an
object membership to a rough set without the need to
define it as opposed to fuzzy memberships functions
(Geng et al., 2008).
Definition 7 (The Rough Membership (Zdzislaw,
1997)). It is the degree of certainty that an object x is
a member of a set X with respect to a set of attributes
B. This is defined as
µ
B
x
=
|B
∗
(X)|
|B(x)|
. (3)
For example, using Table 2 as the universe we let
our target concept X be ({DOC 1, DOC 3, DOC 6},
{cc-a, cc-b, cc-c}); we want to know to what degree
x = DOC 3 actually belongs to X. Thus we calculate
an equivalent class and the B-upper approximation
and determine that for a B = {cc-b}, B(x) = {DOC
1, DOC 2, DOC 3} and B
∗
(X) = {DOC 1, DOC 3}.
Therefore, the rough membership value is µ
B
x
=
2
3
.
2.3 Document Representation
In order to represent documents as objects, we need
to choose a set of well defined semantic descriptors
to be used as attributes within FCA and RST. There
have been efforts to standardise document definitions
based on XML by normalising the internal informa-
tion structures, cf. RossetaNet
1
and ebXML (OASIS,
2001). In this paper we simply subscribe to one of
such efforts.
The Core Components standard (UN/CEFACT,
2003) introduces an initial set of semantic descriptors
to characterise business data and a methodology for
identifying more in particular cases. They are grou-
ped in three types: Basic Core Component, Aggre-
gate Core Component, and Association Core Com-
ponent. The former represents a datum with a spe-
cific business meaning; the second one comprises a
set of Basic Core Components with a related business
meaning; and the third one links two Aggregate Core
Components in a hierarchical structure always leaving
the Basic Core Components as the leaf nodes.
For example, consider the Aggregate Core Com-
ponents address and person and some of their related
Basic Core Components shown below in XML:
<Address>
<BuildingID>42b</BuildingID>
<Street>Baker St</Street>
<City>London</City>
</Address>
<Person>
<Name>Daniel</name>
<FamilyName>Joseph</FamilyName>
</Person>
Just by themselves these Aggregate Core Compo-
nents represent independently an address and a per-
son concepts respectively. But when combined toge-
ther by an Association Core Components the meaning
1
http://www.rossetanet.org
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
376

is different. For instance, the address above can be
associated to the person by a residence concept
2
We
show this in a more elaborated example in which we
also put an extra address within another Aggregate
Core Component as shown below:
<Payment>
<AmountToPay>125.0</AmountToPay>
<PaymentMeans>
<CreditFinancialAccount>
<ID>12345678</ID>
<Owner> <!--Assoc Person-->
<Name>Daniel</Name>
<FamilyName>Joseph</FamilyName>
<Residence><!--Assoc Address-->
<BuildingID>42b</BuildingID>
<Street>Baker St</Street>
<City>London</City>
</Residence>
</Owner>
<FinancialInstitution>
<Name>Bank Ltd</Name>
<Location><!--Assoc Address-->
<BuildingID>15</BuildingID>
<Street>Kind St</Street>
<City>Manchester</City>
</Location>
</FinancialInstitution>
</CreditFinancialAccount>
</PaymentMeans>
</Payment>
Each of the addresses in each of the XML ex-
cerpt above has a semantically meaning depending on
where the concept is within the hierarchical structure
that ultimately represents a document. Therefore in
order to use the concepts whilst keeping the semantic
structure of the document and meaning, we consider
the hierarchical paths from the root element in XML
to the Basic Core Components. Notice that Basic
Core Components can be repeated at different levels
of the hierarchy whilst uniquely representing different
parts of the structure.
For example, using a dot (‘.’) to denote an infix
notation of aggregation and a dash (‘-’) for an as-
sociation between the connected concepts, the paths
Person. Residence- Address. City and Payment. Pay-
mentMeans. CreditFinancialAccount. Owner- Per-
son. Residence- Address. City represent different
meanings of the same City concept due to a seman-
tic structure being kept.
2
The possible concept associations are explicitly shown
at the XML schema level, which is not reflected at the XML
instance level. We refer the interested reader to the Core
Components standard itself (UN/CEFACT, 2003) for fur-
ther details since this is out of the scope of this paper.
Therefore we use such hierarchical paths as attri-
butes within FCA and RST to represent documents.
The detection of these semantic concepts within a do-
cument is left out of the scope of this paper. We as-
sume that existing approaches can extract such an in-
formation from documents, cf. (Laclav´ık et al., 2008).
3 DOCUMENT ALIGNMENT
Our study focuses on the applicability of FCA and
RST to the alignment of documents to specific docu-
ment types as in a business domain. For such a pur-
pose, we call an FCA object x a documentwhose attri-
butes with which it can be represented are in the form
of Core Component paths (named CC paths hereaf-
ter). Thus, we define a document type and a document
alignment as follows.
Definition 8 (Document Type). A document type dt
is a pre-selected (FCA) formal concept such that each
document x
i
∈ G could be represented by a dt. Deter-
mining the formal concept to be a document type is a
subjective decision process by the interested owner of
the document set G.
Definition 9 (Document Alignment Process). Do-
cument alignment is the process to determine the do-
cument type dt that best represents a new document x
(called NewDoc hereafter) to the context K. We can
assume that the number of document types remains
constant for such a context. Notice that a NewDoc
could be represented by many document types, but
one of them should be the most representative.
In order to do this using FCA and RST, the formal
concept X (a document type) with the highest rough
membership value to an equivalence class B(x) has
to be found in the concept lattice. We introduce the
Circle of Interest as a mechanism to build the equiva-
lence class by using a reduced set of documents close
to NewDoc in the concept lattice. Our hypothesis is
that NewDoc is likely to be aligned to the same do-
cument type as one of those documents, thus minimi-
sing the size of equivalence class B(x) to build. We
also present other two mechanisms for comparison
purposes, namely the rough inclusive, and the rough
exclusive.
Notice that our focus is on building the equiva-
lence class rather than improving the similarity mea-
sure as in (Zhao et al., 2006) and (Wang and Liu,
2008). The Circle of Interest and is defined as fol-
lows.
Definition 10 (Circle of Interest). The Circle of In-
terest of a NewDoc x is represented by the set of docu-
ment types assigned to the documents that best match
A STUDY ON ALIGNING DOCUMENTS USING THE CIRCLE OF INTEREST TECHNIQUE
377

x, defined as
N
B
(x) = {best
s
(S) ∪ best
p
(P) ∪
best
t
(x, T) ∪ σ} (4)
where best is a generic function that first calculates
the best match to x from a given set and then obtains
its document type; S is the set of documents to which
x is a sub concept; P is the set of documents to which x
is a super concept; T is the set of documents to which
x is an intersected concept; and σ is simply the set of
document types of the exact matches to NewDoc
3
.
If one or more documents are equal to the best
match to x in a given set, then the assigned document
types of all those documents are returned by the func-
tion best. Moreover, this function uses three different
selection criteria depending on the selection case. As
long as two documents share at least one CC path then
it is possible to describe one document in terms of the
other. Thus we can compare a document h against a
document k based on the number of CC paths shared
with a NewDoc x as defined below for the three com-
parison cases.
Definition 11 (The Sub Concept Case). A document
x is a sub concept of h if h contains all the CC paths
of x but it is not an exact match, and there is a direct
link between the two in the concept lattice. The set S
represents such sub concepts. Thus, given a document
h ∈ S, a documentk ∈ S, and a NewDoc x, h is selected
over the other if h contains less CC paths than k, i.e.
best
s
(S) =
∀h, k ∈ S : h
|h|≤|k|
→ dt
(5)
where x ⊂ h, x ⊂ k, and → obtains the related docu-
ment type.
Definition 12 (The Super Concept Case). A docu-
ment x is a super concept of h if x contains all the CC
paths of h but it is not an exact match, and there is a
direct link between the two in the concept lattice. The
set P represents such super concepts. Therefore, given
a document h ∈ P, a document k ∈ P, and a NewDoc
x, h is selected over the other if h contains more CC
paths than k, i.e.
best
p
(P) =
∀k ∈ P : h
|h|≥|k|
→ dt
(6)
where h ⊂ x, k ⊂ x and → obtains the related docu-
ment type.
Definition 13 (The Intersected Concept Case). A
document x is an intersected concept to h if they share
some of their CC paths without being an exact match,
and there is a direct link to a common super concept
from the two in the concept lattice. The set T contains
3
The authors do not see any pragmatic need to calculate
the “best match” from a set of “exact matches.”
such intersected concepts. Thus, given three docu-
ments d, h, k ∈ T and a NewDoc x, h and k are selected
over d according to the maximum count of absolute
and relative matching CC paths, i.e.
best
t
(x, T) = {AbsC(x, T) ∪ RelC(x, T) → dt} (7)
where → obtains the document types from the resul-
ting set; and
AbsC(x, T) =
∀h, d ∈ T : h
|h ∩ x|≥|d ∩ x|
(8)
is the set of documents with which x shares the grea-
test number of CC paths; and
RelC(x, T) =
∀k, d ∈ T : k
|k ∩ x|
|k|
≥
|d ∩ x|
|d|
(9)
is the set of documents with which x shares the grea-
test percentage of CC paths. Notice that nothing is
said about the relation between h and k, thus it could
be possible that they are the same document.
Obviously if any of the sets S, P, or T is either
empty or contains only one document then there is
no need for a comparison. In the latter case such a
document is selected.
The other two mechanisms we use to build the
equivalence class for comparison purposes, rough in-
clusive and rough exclusive, are defined respectively
as follows.
Definition 14 (Rough Inclusive). The rough inclu-
sive of a NewDoc x is the equivalence class B(x) re-
presenting NewDoc and the documents contributing
with their document types to the Circle of Interest.
That is, its set of attributes B is the greatest attribute
set such that NewDoc and the documents contribu-
ting to the Circle of Interest remain B-indiscernible.
Consequently, the rough inclusive set of documents is
equal or greater than the Circle of Interest. Then this
mechanism includes those document types not origi-
nally found in the Circle of Interest.
Finally,
Definition 15 (Rough Exclusive). The rough exclu-
sive of a NewDoc x is the equivalence class similar to
the rough inclusiveexcept that the document types not
originally found in the Circle of Interest are excluded
from the set.
It seems intuitive that the document types added
by the rough inclusive are less likely to be better re-
presentatives of NewDoc than those of the Circle of
Interest. Yet the rationale for the rough inclusive is to
test whether the right document type for an alignment
was left just outside of the boundary of the Circle of
Interest. Then the rationale for the rough exclusive
is to test whether by adding only extra documents to
the equivalence class without adding their document
types, the rough membership function produces a bet-
ter result than the Circle of Interest alone.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
378
4 EXPERIMENTS
We developed a piece of software for our experiments
(using the FCA colibri-java
4
) and created a concept
lattice of documents using the CC paths to represent
their structure. Part of these documents and their assi-
gned document type comes from real business scena-
rios within the context of our project Commius. Be-
cause the software does not know about document
types, we utilise an approach where the NewDoc is
assumed to be of the document type that we are cal-
culating its rough membership value of, i.e. the cal-
culation of the rough membership can interpreted as
“how much of this document type is the NewDoc.”
This is explained further when describing the experi-
ments themselves.
For our experiments we measure whether a New-
Doc is aligned to the correct document type within
a specific set of documents. Therefore, we calcu-
late the rough membership value of a NewDoc x to
a document type dt (which is a concept X in RST)
of each of the B-indiscernible documents within the
equivalence class. The document type with the hi-
ghest rough membership value is the one selected for
the alignment. If the highest rough membership value
for a particular alignment technique is the same for
multiple document types, we still consider this case
as successful but it is marked as tied. Therefore, we
analyse both the tied and the exact cases of the suc-
cessful alignments.
A NewDoc marked as “wrong” does not imply in-
correct alignment. It is feasible that the composition
of NewDoc is the closest to another document type
in the concept lattice. However, as there is a level of
subjectivity involved in stating whether a document is
more aligned with one document than another, align-
ment is only judged based on whether the stated do-
cument type of NewDoc according to our document
set source, is the same as the software-chosen docu-
ment type that it is aligned with. Such a subjectivity
resembles the difference of preference to information
pieces from one company to another.
4.1 Experiment 1: Varied Number of
Document Type Representatives
For this experiment, we test the three alignment tech-
niques using a different number of documents per do-
cument type. In this case, to build the concept lattice
we use a total of 28 documents consisting of a number
of types namely Sales Order [7 documents], Purchase
Order [5 documents], Quotation [5 documents], Quo-
4
http://code.google.com/p/colibri-java/
tation Request [5 documents], and Sales Invoice [6
documents].
In order to maintain the concept lattice standard
for all tests, the software was asked to align each of
the documents in the lattice with respect to the remai-
ning 27 document. That is, the software considers
each document as if it were the NewDoc for each case,
thus maintaining the document inter-relations static
for the whole experiment.
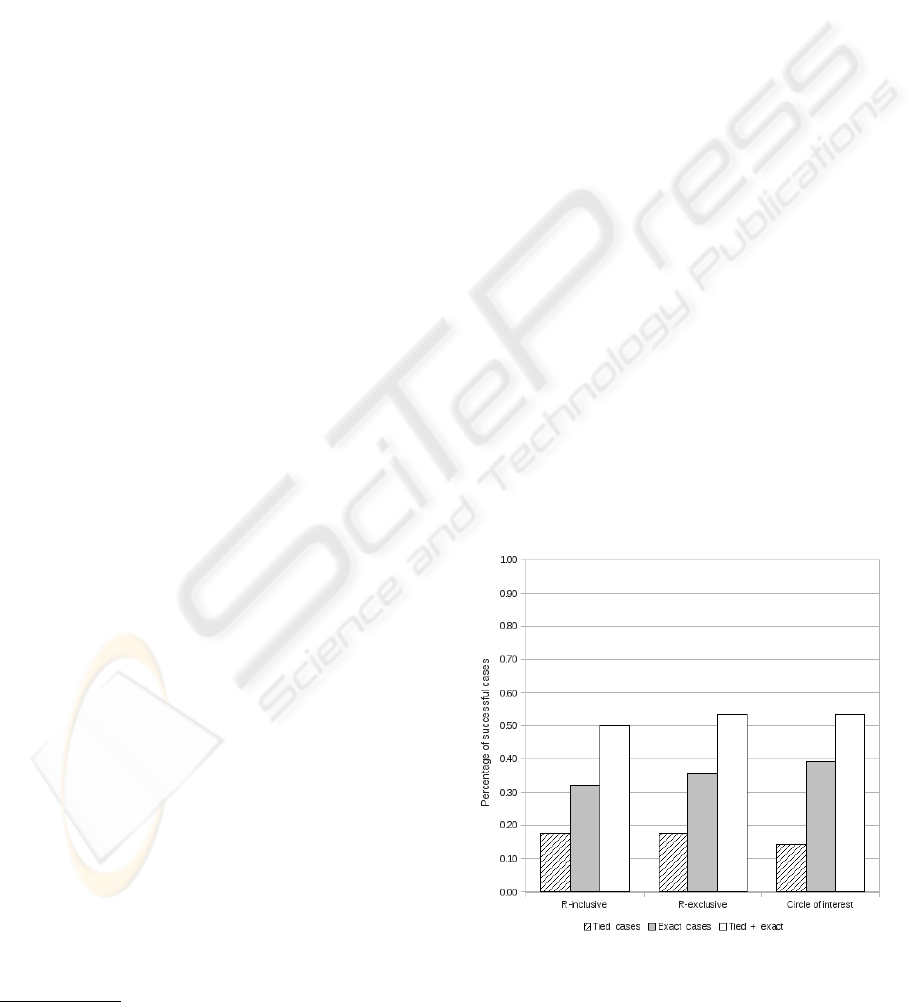
Figure 2 shows the percentage of successful ali-
gnments for each alignment technique. Moreover,
it depicts the percentage of exact matches and tied
matches to the right document type. As can be ap-
preciated, for each of the three techniques the total
percentage is around 50% from which the exact cases
are noticeable higher than the tied cases, yet the ove-
rall is not convincing.
Nevertheless, the exact cases of the Circle of In-
terest is considerable higher than the tied cases, 39%
against 14%. Although the Circle of Interest tech-
nique appears to be the most successful, the margins
between the levels of success of the other techniques
are too small to state conclusively the superiority of
one over the other.
It was noticed empirically that the uneven repre-
sentation of document types skews the concept lattice
by concentrating on those document types with the
most representatives. This results in biasing the align-
ment techniques towards those document types better
represented. In order to reduce such an influence and
possibly increase the successful cases, the number of
representative per document type is then standardised
for the second experiment.
Figure 2: Experiment results with varied number of docu-
ment type representatives.
A STUDY ON ALIGNING DOCUMENTS USING THE CIRCLE OF INTEREST TECHNIQUE
379
4.2 Experiment 2: Equal Number of
Document Type Representatives
For this experiment we test again the three alignment
techniques but using the same number of document
representatives per document type when a NewDoc is
introduced. We use the same set of documents and we
randomly choose four documents per document type
and created a new concept lattice with them, i.e. we
use a total of twenty documents in the concept lattice.
However to represent the introduction of a New-
Doc, a different process was followed: For each docu-
ment type, a “neutral document” of that type is intro-
duced to the lattice. Such a document plays no role in
the count of successful cases, but is used only to keep
the lattice with the same number of document repre-
sentatives whilst the three alignment techniques are
applied to the original four documents for that docu-
ment type. Immediately afterwards, the “neutral do-
cument” is removed from the concept lattice.
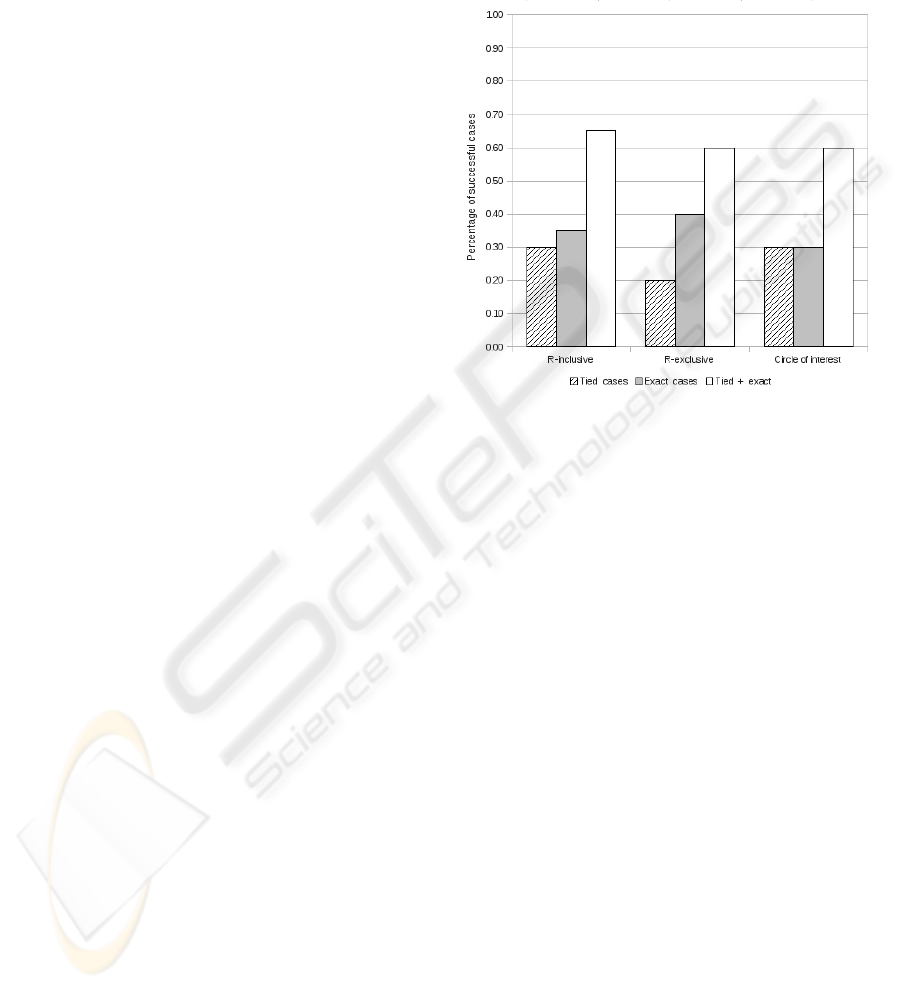
Figure 3 presents the percentages of successful
alignments for each alignment technique. Likewise,
it shows the percentage of tied matches and exact
matches to the correct document type. As can be
seen there is an improvement in the overall success-
ful cases when compared against the first experiment.
In this occasion, the rough inclusive seems the most
successful with 65% of correct cases, however a 30%
of the total is of tied cases which is not significantly
different from a 35% of the total of exact cases. A
similar situation occurs with the Circle of Interest.
On the other hand, the percentage of exact cases
of the rough exclusive (40%) is twice as much as the
tied cases (20%). In the first experiment a similar pro-
portion is maintained for the same technique: 35% of
exact cases and 18% of tied cased, suggesting that this
technique could be promising even with varied num-
ber of document type representatives. Yet a 60% of
total successful cases is arguably good enough.
The overall improvement seems to be due to the
even number of document type representatives. Ho-
wever, a concept lattice with few documents reduces
the number of possible values the rough member-
ship function can return because the size of document
types (concepts) and the equivalence class are smal-
ler, thus increasing the likelihood of tied cases.
Furthermore, the number of attributes with which
a document can be represented also influence the si-
milarity when obtaining the best matches (function
best). That is, a document highly described in terms
of its semantic content will have a large set of attri-
butes. Even if their semantic descriptors represent the
same aggregate semantic concept (Aggregate Core
Component), in the concept lattice they will be dif-
ferent attributes.
Therefore, for our next experimentwe increase the
number of documents likely to be considered for the
equivalence class B(x) by using only the Aggregate
Core Components to describe the documents as ex-
plained further in the following section.
Figure 3: Experiment results with equal number of docu-
ment type representatives.
4.3 Experiment 3: Using Aggregate
Descriptors to Represent
Documents
This experiment is designed to increase the number
of documents to consider when calculating the Circle
of Interest. So we update the representation of docu-
ments by using the CC paths up to Aggregate Core
Components such that they become the leaf nodes of
the hierarchical structure (see Section 2.3), yet Asso-
ciation Core Component are still used. For example,
if a document contains the details of an address
<Address>
<BuildingID>42b</BuildingID>
<Street>Baker St</Street>
<City>London</City>
</Address>
where the inner elements are Basic Core Components,
then the new representation will only contain the Ag-
gregate Core Component like
<Address>
42b Baker St London
</Address>
Thus reducing the number of CC paths used for
representing such a piece of information. Apart from
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
380
that, the experiment set up remains the same as in the
Experiment 2.
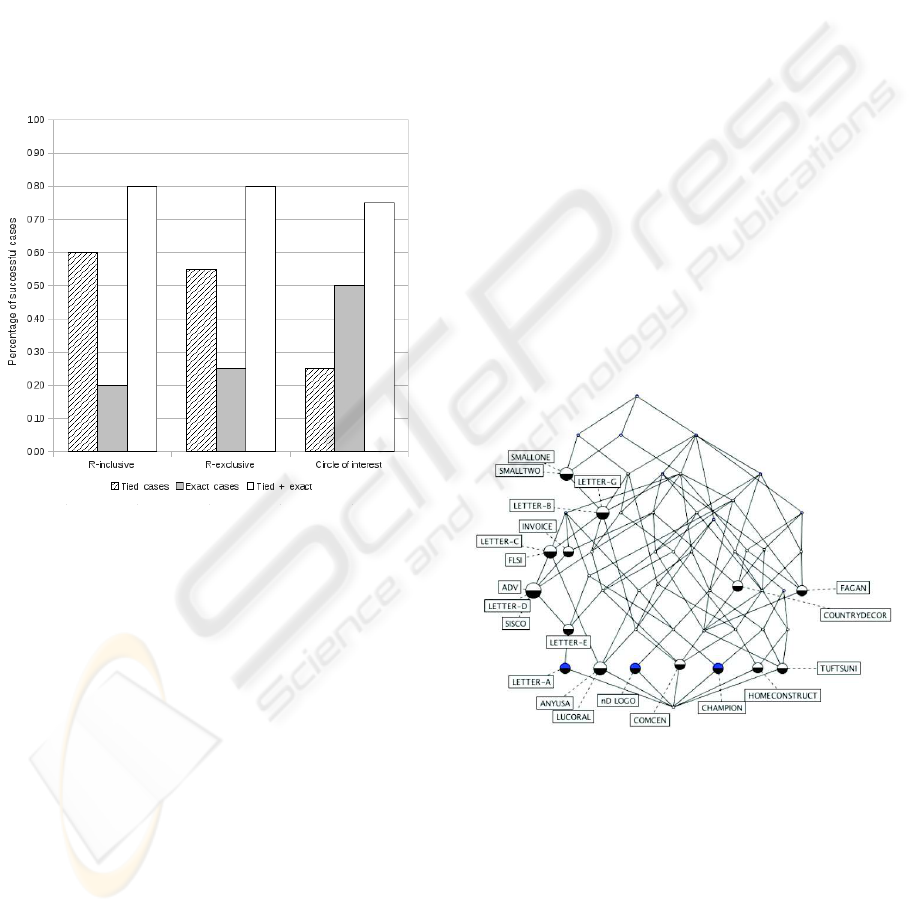
As can be easily appreciated in Figure 4, there is
an increase of successful cases in the three alignment
techniques: for both the rough inclusive and the rough
exclusive there is an 80% of successful cases, whereas
the Circle of Interest is 75%. However, the Circle
of Interest reports a better percentage of exact cases
than its tied counterpart, 50% against 25%, as well
for the other two techniques in which the tied cases
are more than twice the percentage of the exact cases.
The rough inclusive reports a 60% of tied cases and
a 20% of exact cases. The rough exclusive shows a
55% of tied cases and a 25% of exact cases.
Figure 4: Experiment results with aggregate descriptors to
describe documents.
Such results are caused by an increase of the num-
ber of documents that can be represented by a small
set of attributes, which it appears directly co-related
to the reduction of CC paths used to represent a docu-
ment. The Circle of Interest in this case seems nota-
bly better than the other two techniques suggesting its
potential use when the document set contains a large
number of documents represented by a small set of
attributes. Yet the actual co-relation between the two
is out of the scope of this paper.
5 DISCUSSION
The rough exclusive and the rough inclusive seem to
get confused in the Experiment 3 because the number
of tied cases increases considerably when compared
against the Experiment 2. Such a confusion is due to
a super concept - sub concept problem among the do-
cuments. For these two techniques, additional do-
cuments and document types are considered which
might have been pruned by the Circle of Interest tech-
nique. The Circle of Interest pre-analyses the most
similar documents to a NewDoc. This pre-analysis
already considers the super concept sub concept rela-
tionships among the documents, thus such a problem
is not likely to occur when building the equivalence
class in contrast to the other two techniques. Figure
5 shows a concept lattice generated for Experiment
3, where can be appreciated along the left hand side
of the lattice that many instances appear in a super
concept sub concept relationship.
The effectiveness of the Circle of Interest is expo-
sed in the Experiment 3 in which the results show an
increase of exact cases when compared to the Expe-
riment 2 and a higher percentage when compared to
the other techniques within the same experiment. Al-
though appearing empirically sound, the result is not
conclusive because the documents had to be descri-
bed with more general CC paths to increase the simi-
larity of documents by fewer CC paths. This suggests
the potentiality of the Circle of Interest as a technique
for calculating the equivalence class, yet experiments
with a bigger set of documents and comparing against
more common techniques are necessary.
Figure 5: Generated concept lattice for the Experiment 3.
It is also observed in the experiments that having a
small Circle of Interest with a very few document ins-
tances leads to a large number of ties. A small number
of instances in the Circle of Interest would intuitively
reduce the number of possible values for rough mem-
bership calculations. It is necessary then to make this
set of a sufficient size while still maintaining the re-
levance to all document found within. Using the Ag-
gregate Core Components contributes to an enlarged
Circle of Interest as it is more likely that the function
best returns multiple values for each comparison case.
A STUDY ON ALIGNING DOCUMENTS USING THE CIRCLE OF INTEREST TECHNIQUE
381

Alternative methods of enlarging the Circle of Inter-
est, without relying on Aggregate Core Components
is considered for future work.
6 RELATED WORK
Other research efforts have targeted similar problems
for various applications with different degrees of suc-
cess. This section describes the differences between
our approach and other related efforts on (1) FCA and
RST combined, (2) semantic alignment, (3) classifi-
cation, and (4) business related domains.
Indeed, FCA and RST have been used in cluste-
ring and ontology mapping because of their intrin-
sic characteristics which make them suitable for such
tasks. (Bao, 1999) present models and algorithms
to create document clusters by enriching documents
with “approximations” of their own terms then ap-
plying a clustering method using such “approxima-
tions.” Although this approach is applied on docu-
ments, their target problem is different from our own
in the sense that our document types are predefined
“clusters” which a document is to be aligned to, whe-
reas in (Bao, 1999) the approach is to create the clus-
ters.
(Zhao et al., 2006) addresses the problem of on-
tology mapping by introducing an improved simila-
rity measure between two concepts of different onto-
logies. Such an approach differs from ours in that the
Circle of Interest deals with improving the construc-
tion of the equivalence class rather than its evalua-
tion. Moreover, our objective consists of finding an
aligning of a document to a document type (cf. a
concept) whereas in (Zhao et al., 2006) the aim is on
mapping concepts. A more recent effort in improving
the similarity measure is presented in (Wang and Liu,
2008).
The increasing interest in the Semantic Web is at-
tracting efforts on semantic alignment such as Onto-
Morph (Chalupsky, 2000) and FCA-merge (Stumme
and Maedche, 2001). OntoMorph (Chalupsky, 2000)
is a rule based system that uses both syntactic and
semantic “rewriting” mechanisms for merging onto-
logies as symbolic knowledge bases. A recent simi-
lar approach called OntoMerge is presented in (Dou
et al., 2006). In turn FCA-merge (Stumme and
Maedche, 2001) combines ontologies extracted from
documents by merging them in an FCA concept lat-
tice and detecting common concepts, which requires
a knowledge engineer. These approaches target a dif-
ferent problem from ours since they focus on finding a
mapping between ontologies, whereas we use the on-
tology found within a document to find an alignment
to a predefined document type.
Classification can be related to alignment if a tar-
get cluster is sought for a given object. For instance
consider a neural model based on significant vectors
for classifying Reuters news articles (Wermter and
Hung, 2002). Initially clusters have to be defined be-
fore any classification, cf. document types before any
alignment, and the neural model has to be trained with
examples before actually classifying. Yet at runtime
their approach considers the tied cases as a new po-
tential document class. Regardless of the difference
between classification and alignment, FCA by itself
does not need any training at all.
In turn (Cui and Potok, 2006) describes an algo-
rithm where digital documents are clustered by being
modelled as conceptual birds forming flocks. As a
result those birds (documents) flocking together form
a cluster of similar documents. Although they show
that their proposed model achieves clustering with
existing documents, no details are given on what oc-
curs with newly introduced documents.
An E-mail is a form of document exchanged bet-
ween companies, in (Scerri et al., 2007) an approach
called Semanta is introduced to apply speech act
theory to E-mails to interpret and keep track of actions
related to ad-hoc E-mail based workflows. Although
(Scerri et al., 2009) shows Semanta as a supportiveE-
mail based system for workflows, its semantic com-
ponent relies on ontologies based on verbs and nouns
rather than on document alignment, rendering their
problem different from ours.
Finally, another FCA based approach is presen-
ted in (Geng et al., 2008) to find topics of discus-
sion in a set of E-mails using fuzzy membership func-
tions to determine the significance of individual for-
mal concepts in an FCA concept lattice. Their study
differs from ours in that their FCA model creates the
definitions of the document groups whereas our ap-
proach determines whether a document falls into an
already defined group for a specific business domain.
7 CONCLUSIONS
In this paper we present a technique called Circle of
Interest which along with FCA and RST is used for
document alignment. The Circle of Interest is used on
FCA concept lattices to determine a set of document
types closely related to a document to align, thus re-
ducing the size of the equivalence class used by RST
to choose the precise document type from.
Experimenting with documents from real business
scenarios, we demonstrate that our choice for an ali-
gnment is more effective when there is an equal re-
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
382

presentation of document types in the FCA concept
lattice at the point of introduction of a document of
unknown type. It was also shown in the experiments
that using the Circle of Interest as the equivalence
class leads to a more precise alignment, as long as
the number of documents compared to construct the
Circle of Interest is sufficiently large. This supports
the claim that using the Circle of Interest, FCA and
RST is feasible for aligning documents in a business
domain. Future work in this line consists of experi-
menting with a larger set of documents and document
types, and comparing against other techniques.
REFERENCES
Bao, H. T. (1999). Formal Concept Analysis and Rough Set
Theory in Clustering. In The Mathematical Founda-
tion of Informatics. World Scientific Publishing.
Chalupsky, H. (2000). OntoMorph: A Translation System
for Symbolic Knowledge. In Principles of Knowledge
Representation and Reasoning, pages 471—-482.
Cui, X. and Potok, T. E. (2006). A Distributed Agent Im-
plementation of Multiple Species Flocking Model for
Document Partitioning Clustering. In Cooperative In-
formation Agents, volume 4149 of Lecture Notes in
Artificial Intelligence, pages 124–137, Heilderberg.
Springer-Verlag.
Dou, D., McDermott, D., and Qi, P. (2006). Onto-
logy Translation by Ontology Merging and Automa-
ted Reasoning. In Tamma, V., Cranefield, S., Finin,
T. W., and Willmott, S., editors, Ontology for Agents:
Theory and Experiences, Whitestein Series in Soft-
ware Agent Technologies and Autonomic Computing,
pages 73–94. Birkh¨auser, Basel.
Geng, L., Korba, L., Wang, Y., Wang, X., and You,
Y. (2008). Finding Topics in Email Using Formal
Concept Analysis and Fuzzy Membership Functions.
In Advances in Artificial Intelligence: 21st Confe-
rence of the Canadian Society for Computational Stu-
dies of Intelligence, volume 5032 of Lecture Notes in
Artificial Intelligence , pages 108–113, Heilderberg.
Springer-Verlag.
Laclav´ık, M.,
ˇ
Seleng, M., and Hluch´y, L. (2008). Towards
Large Scale Semantic Annotation Built on MapRe-
duce Architecture. In ICCS ’08: 8th International
Conference on Computational Science Part III, pages
331–338, Berlin, Heidelberg. Springer-Verlag.
OASIS (2001). ebXML Technical Architecture Specifica-
tion. Technical report, ebXML.
Pawlak, Z. (1982). Rough sets. International Journal of
Information and Computer Sciences, 11:341–356.
Priss, U. (2006). Formal Concept Analysis in information
science. Annual Review of Information Science and
Technology, 40.
Scerri, S., Davis, B., and Handschuh, S. (2007). Impro-
ving Email Conversation Efficiency through Semanti-
cally Enhanced Email. In Proceedings of the 18th In-
ternational Conference on Database and Expert Sys-
tems Applications, pages 490–494, Washington. IEEE
Computer Society.
Scerri, S., Davis, B., and Handschuh, S. (2009). Se-
manta Supporting E-mail Workflows in Business Pro-
cesses. In Proceedings of the 2009 IEEE Conference
on Commerce and Enterprise Computing, pages 483–
484, Washington. IEEE Computer Society.
Stumme, G. and Maedche, A. (2001). FCA-MERGE:
Bottom-Up Merging of Ontologies. In IJCAI, pages
225–234.
UN/CEFACT (2003). Core Components Technical Specifi-
cation – Part 8 of the ebXML Framework. Technical
report, UN/CEFACT.
Wang, L. and Liu, X. (2008). A New Model of Evalua-
ting Concept Similarity. Knowledge-Based Systems,
21(8):842–846.
Wermter, S. and Hung, C. (2002). Selforganizing classifi-
cation on the Reuters news corpus. In Proceedings of
the 19th international conference on Computational
linguistics, pages 1–7, Morristown, USA. Association
for Computational Linguistics.
Wille, R. (2005). Formal Concept Analysis as Mathema-
tical Theory of Concepts and Concept Hierarchies.
In Ganter, B., Stumme, G., and Wille, R., editors,
Formal Concept Analysis: Foundations and Applica-
tions, Lecture Notes on Artificial Intelligence 3626.
Springer-Verlag, Heilderberg.
Zdzislaw (1997). Rough set approach to knowledge-based
decision support. European Journal of Operational
Research, 99:48–57.
Zhao, Y., Wang, X., and Halang, W. (2006). Ontology
Mapping based on Rough Formal Concept Analy-
sis. In Proceedings of the Advanced International
Conference on Telecommunications and International
Conference on Internet and Web Applications and Ser-
vices. IEEE.
A STUDY ON ALIGNING DOCUMENTS USING THE CIRCLE OF INTEREST TECHNIQUE
383
