
MINING TIMED SEQUENCES TO FIND SIGNATURES
Nabil Benayadi and Marc Le Goc
LSIS Laboratory, University Saint Jerome, Marseille, France
Keywords:
Information-theory, Temporal knowledge discovering, Chronicles models, Markov processes.
Abstract:
We introduce the problem of mining sequential patterns among timed messages in large database of sequences
using a Stochastic Approach. An example of patterns we are interested in is : 50% of cases of engine stops
in the car are happened between 0 and 2 minutes after observing a lack of the gas in the engine, produced
between 0 and 1 minutes after the fuel tank is empty. We call this patterns “signatures”. Previous research
have considered some equivalent patterns, but such work have three mains problems : (1) the sensibility of
their algorithms with the value of their parameters, (2) too large number of discovered patterns, and (3) their
discovered patterns consider only ”after“ relation (succession in time) and omit temporal constraints between
elements in patterns. To address this issue, we present TOM4L process (Timed Observations Mining for
Learning process) which uses a stochastic representation of a given set of sequences on which an inductive
reasoning coupled with an abductive reasoning is applied to reduce the space search. A very simple example
is used to show the efficiency of the TOM4L process against others literature approaches.
1 INTRODUCTION
A ”MonitoringCognitiveAgent” (MCA) is a software
system that aims at monitoring, diagnosing and con-
trolling dynamic processes like manufacturing pro-
cesses, telecommunication networks or web servers.
The main task of an MCA is to analyze the sensor
data provided by the instrumentation to inform about
the observed behavior of the process with timed mes-
sages. Huge amounts of timed messages so collected
in temporal databases (so-called ”event log”). There
is an increasing interest in mining these timed mes-
sages to discover patterns that describe relations be-
tween the variables that govern the dynamic of the
process and so improving its management.
In this paper, we introduce the problems of mining
such a pattern: 50% of cases of engine stops in the car
are happen between 0 and 2 minutes after observing a
lack of the gas in the engine, produced between 0 and
1 minutes after the fuel tank is empty. We call this pat-
terns “signatures”. Finding signatures are valuable in
many fields, for example, when targeting markets us-
ing DM (Direct Mail), market analysts can use signa-
tures to learn what actions they should take and when
they should act to inform their customers to buy. We
propose in this paper the basis of the TOM4L pro-
cess (Timed Observations Mining for Learning pro-
cess) defined to discover signatures among timed
messages in large database of sequences. TOM4L
process avoids also the two remains problems of
Timed Data Mining techniques: the sensitivity of the
Timed Data Mining algorithms with the value of their
parameters and the too large number of generated pat-
terns. TOM4L avoids these two problems with the
use of a stochastic representation of a given set of
sequences on which an inductive reasoning coupled
with an abductive reasoning is applied to reduce the
space search. In the literature, the common charac-
teristic of techniques that mine sequences is the dis-
covery of patterns that are frequents (Agrawal and
Srikant, 1995), (Mannila et al., 1997): the more fre-
quently a pattern occurs, the more likely a pattern is
important. Mining sequential patterns was originally
proposed for market analysis (Agrawal and Srikant,
1995) where the temporal relations between retail
transactions are mined with the AprioriAll algorithm.
This algorithm is based on a interestingness criteria
called the ”support” of a sequential pattern, defined as
the number of time a pattern is observed at least one
time in a sequence. A pattern is then frequent when
its support is greater than a given arbitrary threshold.
Because this approach fails when there is only one
sequence, two principal solutions have been proposed
to gets around of this problem: the Maximal window
size constraint solution and the minimal occurrence
solution (Mannila et al., 1997). The Maximal win-
450
Benayadi N. and Le Goc M. (2010).
MINING TIMED SEQUENCES TO FIND SIGNATURES.
In Proceedings of the 5th International Conference on Software and Data Technologies, pages 450-455
DOI: 10.5220/0003007604500455
Copyright
c
SciTePress
dow size constraint solution devises the sequence in
set of sub-sequences so that a support can be com-
puted (Winepi algorithm). Because the cutting of the
sequence is arbitrary, Minepi algorithm is proposed
that uses the minimal occurrences solution to define
the windows. The problem with these ”Frequential
Approaches” is that the support allows to discover a
lot of frequently observed patterns that are not rep-
resentative of the relations between the process vari-
ables. So ”informativeness” criteria are required to
reduce the set of frequent patterns. The Stochastic
Approach proposes to reverse this sequence mining
process to first identify the potential interesting pat-
terns before looking for frequently observed patterns.
The next section presents a simple illustrative ex-
ample to show the main problems of previous ap-
proaches. Section 3 introduces the basis of the
TOM4L process and the section 4 discusses and com-
pares the results obtained by TOM4L process and oth-
ers literature approaches on the illustrative example.
The section 5 makes a synthesis of the paper and in-
troduces our current works.
2 ILLUSTRATIVE EXAMPLE
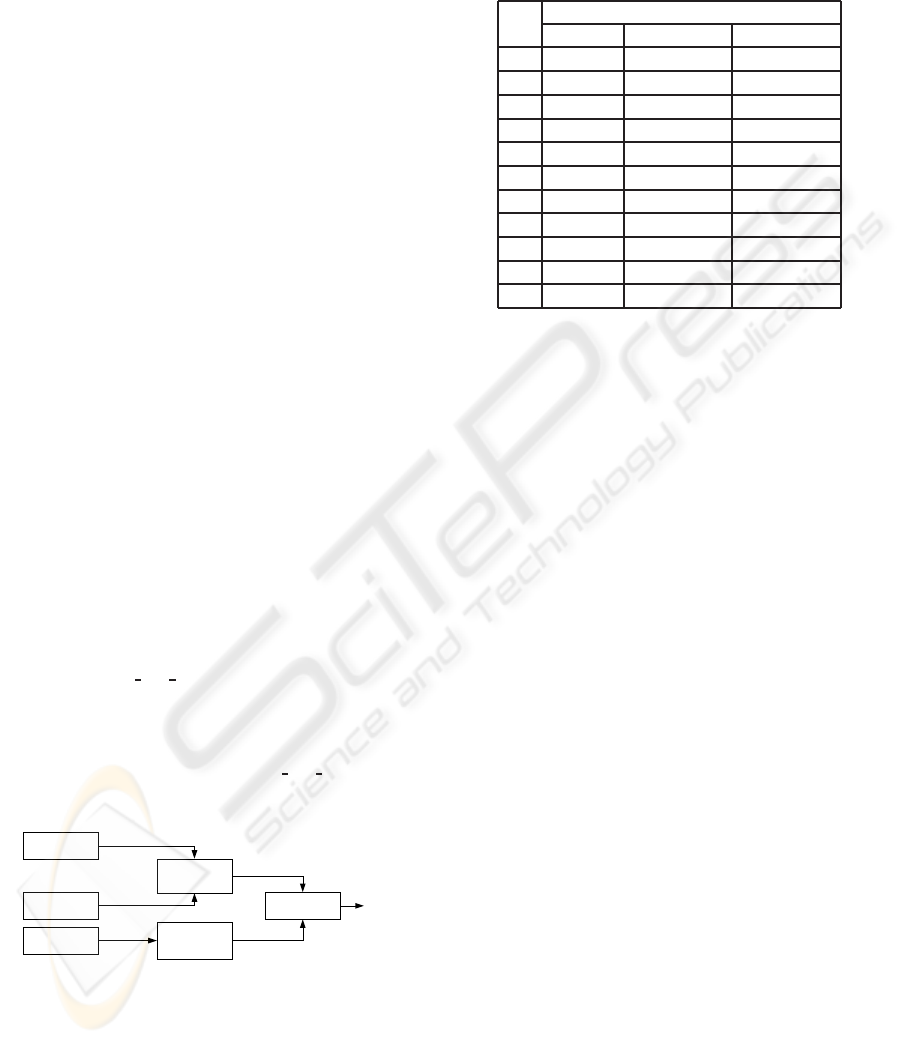
Consider a system that monitors the stopping problem
of a car. Figure 1 shows the structure of the monitored
variables that might affect the stopping of a car. There
are 6 variables (x1,x2,x3,x7,x8,x9) in the car system
that can be assigned to following constants: ∆= {x1 =
{Blown},x2 = {Low},x3 = {Empty},x7 = {Of f },x8 =
{False},x9 = {Does Not Start}}.
Let suppose that the car system was moni-
tored for 30 minutes, this leads to the following
sequence of 100 observations :
ω
= (Low,t
1
),
(Empty,t
2
),(Empty,t
3
),(False,t
4
),(Does Not Start,t
5
),
·· ·, (O f f,t
98
), (Empty,t
99
), (Low,t
100
)}.
c7
electric_
alimentation
c8
gas_
alimentation
c9
engine
c1
fuse
c2
battery
c3
fuel_tank
x1t
x2t
x3 t
x8 t
x9 t
x7 t
Figure 1: Temporal evolution of variables.
To illustrate the sensibility of the ApprioriAll,
Winepi and the Minepi algorithms with the parame-
ters, we defines a set of parameters and apply the al-
gorithms to the sequence
ω
. The window widths W
are set from 2 to 12, and for every window width W,
the window movement v is set to W/3.
The table 1 provides the number of patterns dis-
covered by each algorithm with the set of parameters.
Table 1: Number of discovered patterns.
W
Number of the discovered patterns
Winepi AprioriAll Minepi
2 16 16 27
3 28 28 41
4 51 51 57
5 79 79 74
6 133 133 111
7 211 211 145
8 293 293 197
9 282 282 256
10 381 381 329
11 494 494 464
12 825 825 593
These experimentationsshowthe sensibility of the
Winepi, AprioriAll and the Minepi algorithms with
the parameters: from the first to the end experimen-
tation, the number of patterns increase of more than
5156% for Winepi and AprioriAll, and more than
21961% from Minepi. The main problem is the too
large number of discovered patterns. The paradox is
then the following: to find the ideal set of parameters
that minimizes the number of discovered patterns, the
user must know the system while this is precisely the
global aim of the Data Mining techniques. There is
then a crucial need for another type of approach that is
able to provide a good solution for such a simple sys-
tem and provide operational solutions for real world
systems. The aim of this paper is to propose such an
approach: the TOM4L process which find only 3 re-
lations with the example without any parameters.
3 STOCHASTIC APPROACH
FRAMEWORK
The TOM4L process is based on the Theory of Timed
Observations of (Le Goc, 2006) that defines an in-
ductive reasoning and an abductive reasoning on a
stochastic representation of a set of sequences Ω =
{
ω
i
}, this set not necessarily a singleton. This theory
provides the mathematical foundations of four steps
that reverses the usual Data Mining process in order
to minimize the size of the set of the discovered pat-
terns.
Basic Definitions
A discrete event e
i
is a couple (x
i
,
δ
i
) where x
i
is
the name of a variable and
δ
i
is a constant. The
MINING TIMED SEQUENCES TO FIND SIGNATURES
451

constant
δ
i
denotes an abstract value that can be
assigned to the variable x
i
. The illustrative exam-
ple allows the definition of a set E of six discrete
events: E = {e
1
≡ (x1, Blown), e
2
≡ (x2, Low), e
3
≡
(x3,Empty), e
7
≡ (x7,Of f), e
8
≡ (x8,False), e
9
≡
(x9,Does Not Start)}. A discrete event class C
i
=
{e
i
} is an arbitrary set of discrete event e
i
= (x
i
,
δ
i
).
Generally, the discrete event classes are defined as
singletons because when the constants
δ
i
are inde-
pendent, two discrete event classes C
i
= {(x
i
,
δ
i
)}
and C
j
= {(x
j
,
δ
j
)} are only linked with the vari-
ables x
i
and x
j
(Le Goc, 2006). The illustrative ex-
ample allows the definition of a set Cl of 6 discrete
event classes: Cl = {C
1
= {e
1
}, C
2
= {e
2
}, C
3
= {e
3
},
C
7
= {e
7
}, C
8
= {e
8
}, C
9
= {e
9
}}.
An occurrence o(k) of a discrete event classC
i
= {e
i
},
e
i
= (x
i
,
δ
i
), is a triple (x
i
,
δ
i
,t
k
) where t
k
is the time
of the occurrence. When useful, the rewriting rule
o(k) ≡ (x
i
,
δ
i
,t
k
) ≡ C
i
(k) will be used in the follow-
ing. A sequence Ω = {o(k)}
k=1...n
, is an ordered
set of n occurrences C
i
(k) ≡ (x
i
,
δ
i
,t
k
). For exam-
ple, the illustrative example defines the following se-
quence: Ω = {(C
2
(1), C
3
(2), C
3
(3), C
8
(4), C
9
(5), ··· ,
C
7
(98), C
3
(99), C
2
(100)}. When the constants
δ
i
∈ ∆
are independent, a sequence Ω = {o(k)} defining a
set Cl = {C
i
} of m classes is the superposition of m
sequences
ω
i
= {C
i
(k)} (Le Goc, 2006):
Ω = {o(k)} =
[
i=1...m
ω
i
= {C
i
(k)} (1)
Where each sequence
ω
i
= {C
i
(k)} contains only the
observations of the same class C
i
. For example, the Ω
sequence of the illustrative example is then the super-
position of six sequences
ω
i
= {C
i
(k)}.
3.1 Step 1: Stochastic Representation
The stochastic representation transforms a set of se-
quences Ω in a Markov chain X = (X(t
k
);k > 0)
where the state space Q = {q
i
}, i = 1...m, of X is
confused with the set of m classes Cl = {C
i
} of Ω.
Consequently, two successive occurrences (C
i
(k− 1),
C
j
(k)) correspond to a state transition in X: X(t
k−1
) =
q
i
−→ X(t
k
) = q
j
. The conditional probability
P[X(t
k
) = q
j
|X(t
k−1
) = q
i
] of the transition from a
state q
i
to a state q
j
in X corresponds then to the
conditional probability P
C
j
(k) ∈ Ω|C
i
(k− 1) ∈ Ω
of observing an occurrence of the class C
j
at time t
k
knowing that an occurrence of a class C
i
at time t
k−1
has been observed:
∀i, j, ∀k ∈ K,
P
X(t
k
) = q
j
|X(t
k−1
) = q
i
=
P
C
j
(k) ∈ Ω|C
i
(k− 1) ∈ Ω
≡ p
ij
=
N
ij
m
∑
l,l6=i
N
il
The transition probability matrix P = [p
i, j
] of X
is computed from the contingency table N = [n
i, j
],
where n
i, j
∈ N is the number of couples (C
i
(k),C
j
(k+
1)) in Ω. The stochastic representation of a given
set Ω of sequences is then the definition of a set
R = {R
i, j
(C
i
,C
j
,[
τ
−
ij
,
τ
+
ij
])} where each the condi-
tional probability p
i, j
= P
C
j
(k) ∈ Ω|C
i
(k− 1) ∈ Ω
of each binary relation R
i, j
(C
i
,C
j
,[
τ
−
ij
,
τ
+
ij
]) is not
null. The timed constrains [
τ
−
ij
,
τ
+
ij
] is provided by a
function of the set D of delays D = {d
ij
} = {(t
k
j
−
t
k
i
)} computed from the binary superposition of the
sequences
ω
i, j
=
ω
i
∪
ω
j
:
τ
−
ij
= f
−
(D),
τ
+
ij
= f
+
(D).
For example, the authors of (Le Goc, 2006) use the
properties of the Poisson law to compute the timed
constraints:
τ
−
ij
= 0,
τ
+
ij
=
1
λ
i, j
where
λ
i, j
is the Pois-
son rate (i.e. the exponential intensity) of the expo-
nential law that is the average delay d
ij
moy
=
∑
(d
ij
)
Card(D)
.
The set R of the illustrative example is a set of 26
binary relations : R = {R
i, j
(C
i
,C
j
,[
τ
−
i, j
,
τ
+
i, j
])} where
p
i, j
=
n
i, j
n
i
> 0.
3.2 Step 2: Induction of Binary
Relations
Considering a binary relation R
i, j
(C
i
,C
j
,[
τ
−
ij
,
τ
+
ij
]), a
sequence Ω defining the set Cl of m classes with n
occurrences contains n − 1 couples (o(k), o(k + 1)).
Each of them is one of the four following types:
(C
i
(k),C
j
(k + 1)), (C
i
(k),C
j
(k + 1)), (C
i
(k),C
j
(k +
1)), and (C
i
(k),C
j
(k + 1)), where C
i
(resp. C
j
) is
an abstract class denoting any classes of Cl except
C
i
(resp. C
j
). The n − 1 couples (o(k),o(k + 1))
can then be seen as n− 1 realizations of one of the
four relations linking two abstract binary variables X
and Y of a discrete binary memoryless channel in a
communication system according to the information
theory (Shannon, 1949), where X(t
k
) ∈ {C
i
,C
i
} and
Y(t
k+1
) ∈ {C
j
,C
j
} (Figure 2). To use this model, the
Figure 2: Two abstract binary variables connected by a dis-
crete memoryless channel.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
452

number of occurrences of the abstract classes C
i
and
C
j
can not be the number of the occurrences of the
classes Cl −C
i
and Cl −C
j
but an average value:
• n
i, j
is the number of couples (C
i
(k),C
j
(k+ 1)) in
Ω.
• n
i, j
is the average number of couples
(C
i
(k),C
j
(k+ 1)) in Ω:
• n
i, j
=
1
m− 1
∑
∀C
l
∈C
j
n
i,l
.
• n
i, j
is the average number of couples
(C
i
(k),C
j
(k+ 1)) in Ω:
• n
i, j
=
1
m− 1
∑
∀C
l
∈C
i
n
l, j
• n
i, j
is the average number of couples
(C
i
(k),C
j
(k+ 1)) in Ω:
• n
i, j
=
1
(m− 1)
2
∑
∀C
l
∈C
i
,∀C
f
∈C
j
n
l, f
This leads to m·(m−1) binary contingency tables
of the form of the Table 2.
Table 2: Contingency table for X and Y.
@
@
X
Y
C
j
C
j
∑
C
i
n
i, j
n
i, j
n
i
=
∑
y∈{ j, j}
n
i,y
C
i
n
i, j
n
i, j
n
i
=
∑
y∈{ j, j}
n
i,y
∑
n
j
=
∑
x∈{i,i}
n
x, j
n
j
=
∑
x∈{i,i}
n
x, j
N =
∑
x∈{i,i},y∈{ j, j}
n
x,y
These contingency tables allow computing
two conditional probabilities matrix P
s
(i.e.
P(Y(t
k+1
)|X(t
k
))) and P
p
(i.e. P(X(t
k
)|Y(t
k+1
)).
These two matrix allow the definition of the BJ-
measure to build a criterion to evaluate the interest of
a binary relation R
i, j
(C
i
,C
j
,[
τ
−
ij
,
τ
+
ij
]).
3.2.1 Interestingness of Binary Relations
The idea for defining an efficient interestingness
criterion to induce binary relations is that if know-
ing C
i
(k) increases the probability of observing
C
j
(k + 1) (i.e. p(C
j
|C
i
) > p(C
j
)), then the ob-
servation C
i
(k) provides some information about
an observation C
j
(k + 1) (Blachman, 1968). We
propose then to use the distance of Kullback-Leibler
D(p(Y|X = C
i
)kp(Y)) to evaluate the relation
between the a priori distribution p(C
j
) of an observa-
tion C
j
(k) and the conditional distribution p(C
j
|C
i
):
D(p(Y |X = C
i
)kp(Y)) =
p(Y = C
j
|X = C
i
) ×log
2
p(Y=C
j
|X=C
i
)
p(Y=C
j
)
+
p(Y = C
j
|X = C
i
) ×log
2
p(Y=C
j
|X=C
i
)
p(Y=C
j
)
(2)
In order to remove the symmetry introduced when
evaluating the relation R
i, j
(C
i
,C
j
) and R
i, j
(C
i
,C
j
) ,
we propose to use an oriented Kullback-Leibler dis-
tance, called BJL.
Definition 1. The BJL-measure BJL(C
i
,C
j
) of binary
relation R(C
i
,C
j
) is the right part of the Kullback-
Leibler distance D(p(Y|X = C
i
)kp(Y)):
• p(Y = C
j
|X = C
i
) < p(Y = C
j
) ⇒ BJL(C
i
,C
j
) =
0
• p(Y = C
j
|X = C
i
) ≥ p(Y = C
j
) ⇒ BJL(C
i
,C
j
) =
D(p(Y|X = C
i
)kp(Y))
The BJL(C
i
,C
j
) is the information brought by the
occurrences of the class C
i
about the occurrences of
the class C
j
. The Kullback-Leibler distance can be
written as the sum of two BJL as follow:
D(p(Y|C
i
)kp(Y)) = BJL(C
i
,C
j
) + BJL(C
i
,C
j
) (3)
Contrary to Kullback-Leibler distance,
BJL(C
i
,C
j
) is an asymmetric measure which
differently evaluates the binary relations R
i, j
(C
i
,C
j
)
and R
i, j
(C
i
,C
j
) . The same reasoning can be done
when considering the information distribution be-
tween the predecessors X(t
k
) = C
i
or X(t
k
) = C
i
of
the assignation Y(t
k+1
) = C
j
:
Definition 2. The BJW-measure BJW(C
i
,C
j
) of
binary relation R(C
i
,C
j
) is the right part of the
Kullback-Leibler distance D(p(X|Y = C
j
)kp(X)):
• p(X = C
i
|Y = C
j
) < p(X = C
i
) ⇒ BJW(C
i
,C
j
) =
0
• p(X = C
i
|Y = C
j
) ≥ p(X = C
i
) ⇒ BJW(C
i
,C
j
) =
D(p(X|Y = C
j
)kp(X))
Both the BJL(C
i
,C
j
) and BJW(C
i
,C
j
) measures
are combined in a single measure called BJM(C
i
,C
j
):
Definition 3. The BJM-measure BJM(C
i
,C
j
) of a
binary relation R(C
i
,C
j
) is the norm of the vector
BJL(C
i
,C
j
)
BJW(C
i
,C
j
)
:
• (p(C
j
|C
i
) ≥ p(C
j
)) ∨ (p(C
i
|C
j
) ≥ p(C
i
)) ⇒
BJM(C
i
,C
j
) =
p
BJL(C
i
,C
j
)
2
+ BJW(C
i
,C
j
)
2
• (p(C
j
|C
i
) < p(C
j
)) ∨ (p(C
i
|C
j
) < p(C
i
)) ⇒
BJM(C
i
,C
j
) = −
q
BJL(C
i
,C
j
)
2
+ BJW(C
i
,C
j
)
2
MINING TIMED SEQUENCES TO FIND SIGNATURES
453
The minus sign is used to build a monotonous
measure that distinguishes the position of a relation
R(C
i
,C
j
) around the independence point. The BJM-
measure BJM(C
i
,C
j
) of a relation R(C
i
,C
j
) is then
simply:
BJM(C
i
,C
j
) =
q
BJL(C
i
,C
j
)
2
+ BJW(C
i
,C
j
)
2
−
q
BJL(C
i
,C
j
)
2
+ BJW(C
i
,C
j
)
2
The maximum value BJM(C
i
,C
j
)
max
(obtained
when n
i, j
= min(n
i
,nj)) and the minimum value of
BJM(C
i
,C
j
)
min
(obtained when n
i, j
= 0) depend on
the ratio
θ
i, j
=
n
i
n
j
. The comparison of two BJM-
measures is not possible. To avoid this problem, the
BJM-measure BJM(C
i
,C
j
) is made linear with a M-
measure M(C
i
,C
j
) defined as follows:
Definition 4.
M(C
i
,C
j
) =
1
2
·
BJM(C
i
,C
j
)
BJM(C
i
,C
j
)
max
+
1
2
if p(C
j
|C
i
) > p(C
j
)
−
1
2
·
BJM(C
i
,C
j
)
BJM(C
i
,C
j
)
min
+
1
2
else
Whatever is the ratio
θ
i, j
, the M-measure M(C
i
,C
j
)
as the following properties:
• M(C
i
,C
j
) = 1 ⇔ BJM(C
i
,C
j
) = BJM(C
i
,C
j
)
max
(ideal crisscross)
• M(C
i
,C
j
) = 0,5 ⇔ BJM(C
i
,C
j
) = 0 (C
i
and C
j
are independent)
• M(C
i
,C
j
) = 0 ⇔ BJM(C
i
,C
j
) = BJM(C
i
,C
j
)
min
(C
i
and C
j
are not linked)
For example, the values of the M-measure of the 26
binary relations of R of the illustrative example are
given in table 3. The measure M can finally used as
Table 3: Matrix M.
M C
1
C
2
C
3
C
7
C
8
C
9
C
1
0.56 0 0 0.8 0 0
C
2
0 0 0 0.64 0 0
C
3
0 0.52 0.49 0 0.54 0
C
7
0 0 0.501 0 0 0.59
C
8
0 0.501 0.51 0 0 0.59
C
9
0 0.51 0.54 0 0.51 0
interestingness criterion for inducing binary relations
as follows :
M(C
i
,C
j
) > 0.5 ⇒ R
i, j
(C
i
,C
j
) ∈ I (4)
For example, the set I of binary relations that
can be induced from R of the illustrative ex-
ample contains 13 binary relations : I =
{R(C
1
,C
1
,[
τ
−
1,1
,
τ
+
1,1
]),R(C
1
,C
7
,[
τ
−
1,7
,
τ
+
1,7
]),·· · }.
3.3 Step 3: Deduction of n-ary Relations
The set I of binary relations contains then the minimal
subset of R where each relation R
i, j
(C
i
,C
j
) presents
a potential interest. From this set, we can build a
set of n-ary relations having some potential to be ob-
served in the initial set Ω of sequences. To this aim,
an heuristic h(m
i,n
) can be used to guide an abduc-
tive reasoning to build a minimal set M = {m
k,n
} of
n-ary relations of the form m
k,n
= {R
i,i+1
(C
i
,C
i+1
)},
i = k, · · · ,n− 1, that is to say paths leading to a partic-
ular final observation class C
n
. The heuristic h(m
i,n
)
makes a compromise between the generality and the
quality of a path m
i,n
:
h(m
i,n
) = card(m
i,n
) × BJL(m
i,n
) × P(m
i,n
) (5)
In this equation, card(m
i,n
) is the number of relations
in m
i,n
, BJL(m
i,n
) is the sum of the BJL-measures
BJL(C
k−1
,C
k
) of each relation R
k−1,k
(C
k−1
,C
k
) in
m
i,n
and P(m
i,n
) corresponds to the Chapmann-
Kolmogorovprobability of a path in the transition ma-
trix P = [p(k−1,k)] of the Stochastic Representation.
The interestingness heuristic h(m
i,n
) being of the form
φ
· ln(
φ
), it can be used to build all the paths m
i,n
where h(m
i,n
) is maximum (Benayadi and Le Goc,
2008a). For the illustrative example, let suppose that
we are interested by explaining observations of the
class C
9
(C
9
= {e
9
≡ (x9,Does Not Start)}). So, the
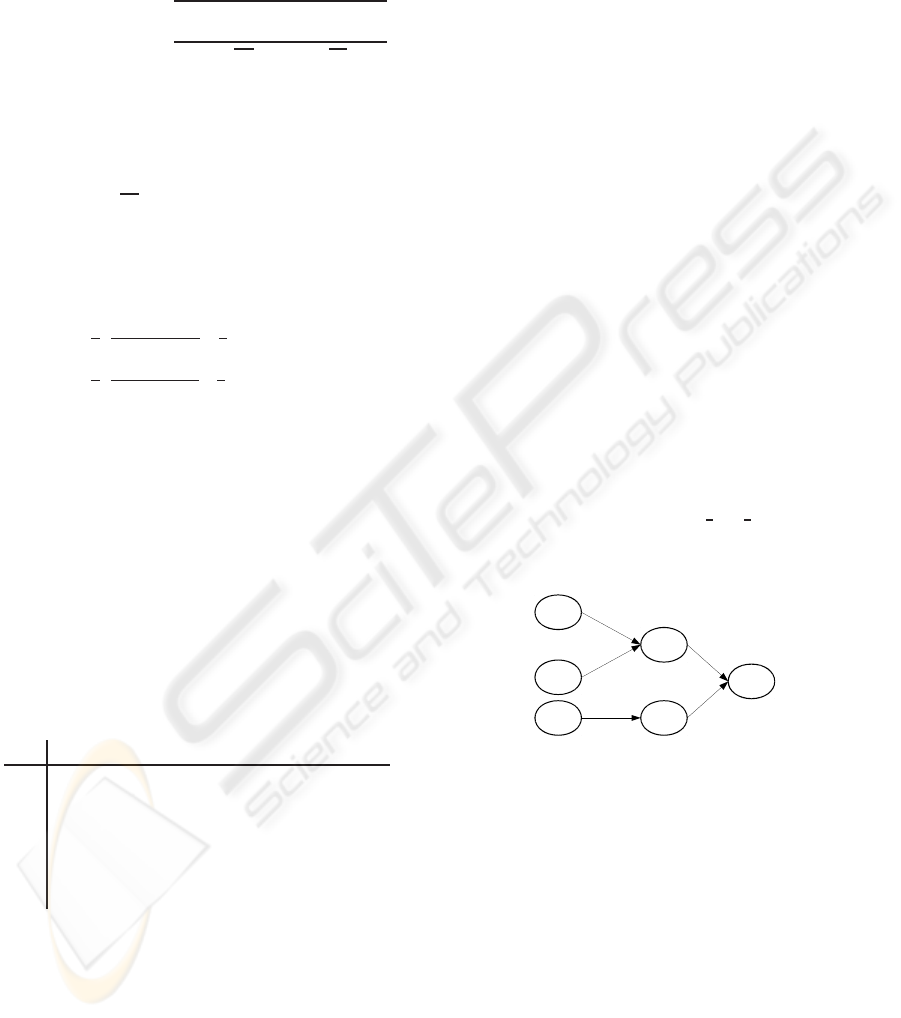
deduction step found three n-ary relations leading to
the class C
9
(Figure 3).
C
9
C
7
C
8
C
2
C
1
C
3
[
7,9
,
7,9
]
[
8,9
,
8,9
]
[
3,8
,
3,8
]
[
2,7
,
2,7
]
[
1,7
,
1,7
]
Fuse= blown
Battery= low
Power= off
Gas in Engine= false
Engine behavior =does not start , stops
Fuel Tank =empty
Figure 3: The discovered three n-ary relations.
3.4 Step 4: Find Representativeness
n-ary Relations
Given a set M = {m
k,n
)} of paths m
k,n
=
{R
i,i+1
(C
i
,C
i+1
)}, i = k,·· · ,n − 1, the TOM4L
process uses two representativeness criteria to build
the subset S ⊆ M containing the only paths m
k,n
being representative according the initial set Ω of
sequences. These criteria are a timed version of
support and confidence notions:
Definition 5. Anticipation Rate. The anticipation
rate Ta(m
i,n
) of a n-ary relation m
i,n
is the ratio
between the number of instances of m
i,n
in Ω with
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
454

the number of occurrences of the m
i,n−1
(i.e. the
n-ary relation m
i,n
without the last binary relation
R
n−1,n
(C
n−1
,C
n
)).
Definition 6. Cover Rate. The cover rate Tc(m
i,n
) of
a n-ary relation m
i,n
is the ratio between the number
of occurrences of m
i,n
with the number of occurrences
of the final class C
n
of the n-ary relation m
i,n
.
When an n-ary relation m
i,n
satisfies these crite-
ria, m
i,n
is called a signature (Benayadi and Le Goc,
2008b). For Ta = 25% and Tc = 20%, all the n-ary
relations of the set M of the illustrative example are
signatures (S = M). These signatures are the only re-
lations (patterns) that are linked with the car system.
4 DISCUSSION
To evaluate the performance of TOM4L process, we
will report on the results obtained on the car exam-
ple (section 2) by TOM4L process and the three pop-
ular timed data mining algorithms Winepi(Mannila
et al., 1997), AprioriAll (Agrawal and Srikant, 1995)
and Minepi (Mannila et al., 1997). It shows that the
TOM4L process outperforms Winepi, AprioriAll and
Minepi in terms of the number of discovered patterns
and theirs accuracy. As we can see from the table
1 and the figure 3, TOM4L process outperforms the
three algorithms Winepi, AprioriAll and Minepi in
terms of number of the discovered patterns. Further-
more, TOM4L discovers patterns witch are consis-
tent with the structural model of the car system, while
most of the patterns discovered by Winepi, AprioriAll
and Minepi contradict this structural model.
Also, the three algorithms Winepi, AprioriAll and
Minepi require the setting of a set of parameters, so
the discovered patterns depend therefore on the val-
ues of this parameters (Mannila, 2002). To obtain an
interesting patterns, we must found the ideal set of pa-
rameters witch need to have some a priori knowledge
about the car system while this is precisely the global
aim of the Data Mining techniques.
Others experiments were made on sequences gen-
erated by complex dynamic process as blast furnace
process where they show that TOM4L approach con-
verges towards a minimal set of operational relations
and outperforms Winepi, AprioriAll and Minepi.
5 CONCLUSIONS
This paper presents the basis of the TOM4L process
for discovering temporal knowledge from timed mes-
sages generated by monitored dynamic process. The
TOM4L process is based on four steps: (1) a stochas-
tic representation of a given set of sequences from
which is induced (2) a minimal set of timed binary
relations, and an abductive reasoning (3) is then used
to build a minimal set of n-ary relations that is used to
find (4) the most representativen-ary relations accord-
ing to the given set of sequences. The induction and
the abductive reasoning are based on an interesting-
ness measure of the timed binary relations that allows
eliminating the relations having no meaning accord-
ing to the given set of sequences. Our experiment
on a very simple illustrative process, the car system
shows that TOM4L process outperforms literature ap-
proaches.
REFERENCES
Agrawal, R. and Srikant, R. (1995). Mining sequential pat-
terns. Proceedings of the 11th International Confer-
ence on Data Engineering (ICDE95), pages 3–14.
Benayadi, N. and Le Goc, M. (2008a). Discovering tempo-
ral knowledge from a crisscross of observations timed.
The proceedings of the 18th European Conference on
Artificial Intelligence (ECAI’08). University of Patras,
Patras, Greece.
Benayadi, N. and Le Goc, M. (2008b). Using a measure of
the crisscross of series of timed observations to dis-
cover timed knowledge. In Proceedings of the 19th
International Workshop on Principles of Diagnosis
(DX’08), Blue Mountains, Australia.
Blachman, N. M. (1968). The amount of information that
y gives about x. IEEE Transcations on Information
Theory IT, 14.
Le Goc, M. (2006). Notion d’observation pour le diagnostic
des processus dynamiques: Application `a Sachem et `a
la d´ecouverte de connaissances temporelles. HDR,
Facult´e des Sciences et Techniques de Saint J´erˆome.
Mannila, H. (2002). Local and global methods in data min-
ing: Basic techniques and open problems. 29th In-
ternational Colloquium on Automata, Languages and
Programming.
Mannila, H., Toivonen, H., and Verkamo, A. I. (1997). Dis-
covery of frequent episodes in event sequences. Data
Mining and Knowledge Discovery, 1(3):259–289.
Shannon, C. E. (1949). Communication in the presence of
noise. Institute of Radio Engineers, 37.
MINING TIMED SEQUENCES TO FIND SIGNATURES
455
