p-MDAG

A Parallel MDAG Approach

Joubert de Castro Lima

and Celso Massaki Hirata

Federal University of Ouro Preto (UFOP), Brazil

Instituto Tecnológico de Aeronáutica (ITA), Brazil

Keywords: Cube Computation, Parallel Cube Computation, Data Warehous, OLAP.

Abstract: In this paper, we present a novel parallel full cube computation approach, named p-MDAG. The p-MDAG

approach is a parallel version of MDAG sequential approach. The sequential MDAG approach outperforms

the classic Star approach in dense, skewed and sparse scenarios. In general, the sequential MDAG approach

is 25-35% faster than Star, consuming, on average, 50% less memory to represent the same data cube. The

p-MDAG approach improves the runtime while keeping the low memory consumption; it uses an attribute-

based data cube decomposition strategy which combines both task and data parallelism. The p-MDAG

approach uses the dimensions attribute values to partition the data cube. It also redesigns the MDAG

sequential algorithms to run in parallel. The p-MDAG approach provides both good load balance and

similar sequential memory consumption. Its logical design can be implemented in shared-memory,

distributed-memory and hybrid architectures with minimal adaptation.

1 INTRODUCTION

The Data Warehouse (DW) and Online Analytical

Processing (OLAP) technologies perform data

generalization by summarizing huge amount of data

at varying levels of abstraction. They are based on a

multidimensional model. The multidimensional

model views the stored data as a data cube. The data

cube was introduced in (Gray, 1997). It is a

generalization of the group-by operator over all

possible combinations of dimensions with various

granularity aggregates. Each group-by, named

cuboid or view, corresponds to a set of cells,

described as tuples over the cuboid dimensions.

Since the introduction of DW and OLAP,

efficient computation of cubes has become one of

the most relevant and pervasive problems in the DW

area. The problem is of exponential complexity with

respect to the number of dimensions; therefore, the

materialization of a cube involves both a huge

number of cells and a substantial amount of time for

its generation.

One alternative for dealing with the data cube

size is to allow partial cube computation. Instead of

computing the full cube, a subset of a given set of

dimensions or a smaller range of possible values for

some of the dimensions is computed. We have

iceberg-cubes (Beyer, 1999) (Han, 2001) (Lima,

2007) (Xin, 2007), closed-cubes (Xin, 2006),

quotient-cubes (Lakshmanan, 2002) and frag-cubes

(Li, 2004) which address different solutions to

compute partial data cubes.

The second alternative for dealing with the data

cube size is to introduce parallel processing which

can increase the computational power through

multiple processors. Moreover, the parallel

processing can increase the IO bandwidth through

multiple parallel disks. There are several parallel

cube computation and query approaches in the

literature (Chen, 2004) (Chen, 2008) (Dehne, 2001)

(Dehne, 2002) (Goil, 1997) (Goil, 1998) (Goil,

1999) (Lu, 2003) (Muto, 1999).

In this paper, we present a novel parallel

approach to compute data cubes named Parallel

Multidimensional Direct Acyclic Graph Approach

(p-MDAG). The p-MDAG approach combines both

data and task parallelism. It is designed to be

executed in distributed-memory, shared-memory or

hybrid architectures. Low cost hybrid architecture

can be represented by a cluster of multiprocessor

PCs interconnected by a network or switch.

The p-MDAG approach uses the dimensions

attribute values to partition the data cube. It also

redesigns the two phase (base and aggregation

322

de Castro Lima J. and Hirata C. (2010).

p-MDAG - A Parallel MDAG Approach.

In Proceedings of the 12th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages

322-331

DOI: 10.5220/0003017703220331

 SciTePress

phases) MDAG sequential algorithms to run in

parallel.

The MDAG approach, proposed in (Lima, 2007),

outperforms the Star approach, proposed in (Xin,

2007), in dense, skewed and sparse scenarios,

computing full or iceberg cubes. The Star approach

outperforms some classical cube approaches, as

presented in (Zhao, 1997), (Beyer, 1999) and (Han,

2001), in the same scenarios. In general, the MDAG

approach is 25-35% faster than Star, using, on

average, 50% less memory to represent the same

data cube.

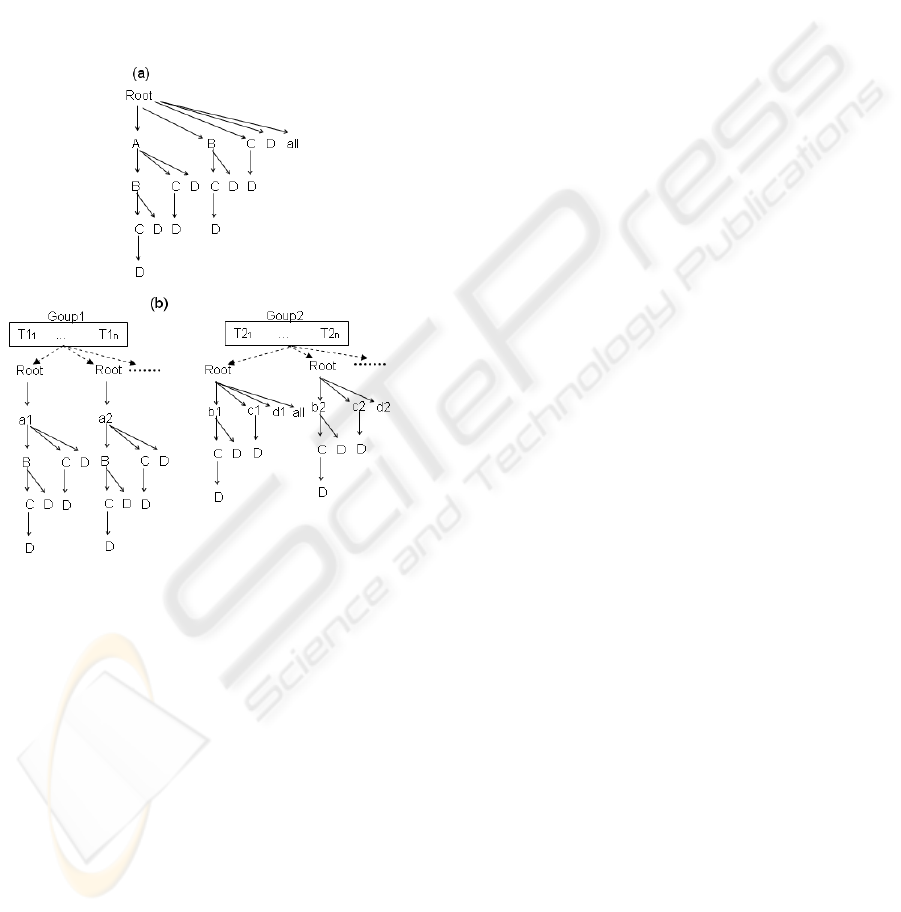
Figure 1: p-MDAG decomposition strategy.

Figure 1 illustrates the basis of p-MDAG data

cube decomposition strategy. In Figure 1, we

illustrate a data cube composed by four dimensions

A, B, C and D with cardinalities C

, C

and C

respectively. We consider A={a

; a

; . . .}, B={b

;

; . . .}, C={c

; c

; . . .} and D={ d

; d

; . . .}.

In Figure 1-a, we have a unique lattice of

cuboids, representing the cuboids A, B, C, D, AB,

AC, AD, BC, BD, CD, …, ABCD, all(*). We use a

prefixed data structure to represent such cuboids. A

path from root to a node represents a cuboid.

The challenge is to find a set of disjoint cube

partitions with similar size and a set of parallelizable

tasks during the cube computation. In Figure 1-b, we

first divide the lattice into partitions rooted by A

attribute values. These partitions form the cuboids

ABCD, ABC, AB and so on. The base cuboid

ABCD is created from the base relation and the

remaining aggregated cuboids are created from the

base cuboid, in a top-down fashion. All the cuboids

rooted by A attribute values are created by the thread

group 1.

In Figure 1, T1

, … T1

, T2

, … T2

represent

the threads. The number of threads in a group

depends on the number of processors in a machine.

The number of partitions that each thread handles

depends on the frequency of the attribute values of

the dimensions. If the data is skewed, we can adopt

sampling techniques to identify the approximate

frequencies without full base relation scans.

After the execution of thread group 1, the thread

group 2 starts its execution. The number of threads

on both groups is not necessarily identical. We use

identical thread group size to facilitate the

explanation.

The second thread group creates the remaining

cuboids, i.e., cuboids not started with dimension A

(BCD, BC, B and so on). The threads in the second

group are associated to the remaining dimensions

attribute values. They read the partitions generated

by the thread group 1 and update their own cube

partitions. After the second thread group execution,

the full cube is complete.

In summary, the p-MDAG approach minimizes

regions of the algorithms that must be run

sequentially. These regions are limited to the thread

groups configuration, start-up and join. No

synchronization is required to generate the

aggregated cuboids. The p-MDAG approach

achieves a good load balance, since each partition

have similar size. Finally, p-MDAG and MDAG

have similar memory consumption. The unique

redundancy in p-MDAG approach is the internal

node. Each cube partition has its shared internal

nodes to avoid synchronizations, but the number of

internal nodes is insignificant when compared with

the number of non internal nodes.

We run the p-MDAG approach using base

relations with different cardinalities, dimensions

tuples and skew. In general, the p-MDAG approach

scales very well in a shared-memory multiprocessor

machine, where a linear speedup is not reachable to

a memory-bound application, since the intensive

memory access increases the bus system contention.

Most bus-based systems do not scale well because of

contention on the bus (Dongarra, 2003).

The remaining of the paper is organized as

follows: Section 2 the sequential MDAG approach is

explained. In Section 3, the p-MDAG approach is

explained in details, the algorithms are described

and the performance results are presented.

Discussion on the potential extensions and

p-MDAG - A Parallel MDAG Approach

323

limitations of the p-MDAG approach is described in

Section 4. We conclude our work in Section 5.

2 MDAG APPROACH

The sequential MDAG approach, proposed in (Lima,

2007), computes a full cube in two phases: first, it

scans the base relation to generate the base cuboid;

second, it scans the base cuboid to generate the

aggregated cuboids. The aggregated cuboids are

generated in a top-down fashion.

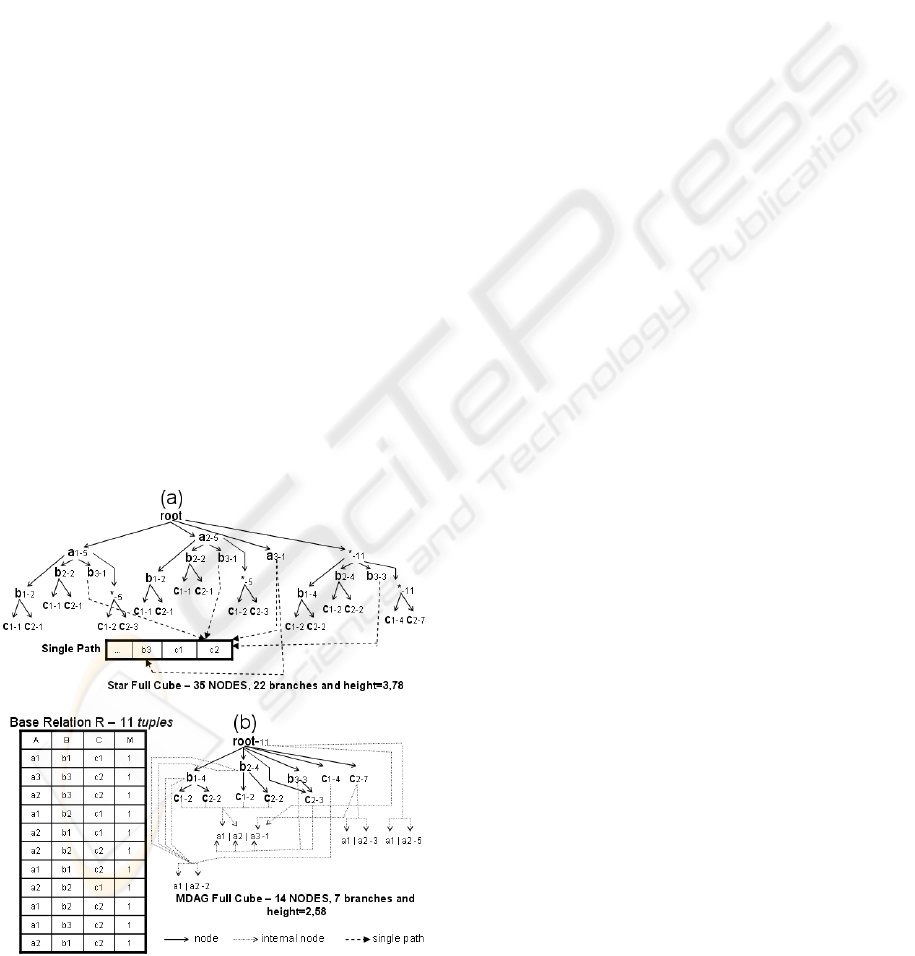
The MDAG approach uses internal nodes in a

data cube representation to reduce the number of

redundant nodes. The presence of internal nodes also

reduces both the number of branches and the height

of the MDAG cube representation, as Figure 2

illustrates. During the base and aggregated cuboids

construction, the MDAG guarantees no internal node

redundancies in the lattice.

Figure 2 illustrates Star and MDAG full cubes,

computed from R. R is a base relation with 11

tuples, one measure and three dimensions (ABC)

with cardinalities 3, 3 and 2, respectively.

The MDAG approach uses Direct Acyclic

Graphs (DAGs) to represent individual cuboids. In

Figure 2-b, a path from root to a leaf node or a path

from root to leaf node plus an internal node

represents a MDAG cube cell. In Figure 2-a, a path

from root to a leaf node represents a Star cube cell.

Figure 2: Star and MDAG full cubes.

During the aggregated cuboids construction,

there are several single paths in the lattice. Consider

a single path a branch of a data structure where no

forks exist. In Star approach, the first node of the

single path points to some attribute values and the

remaining single path nodes are removed, as Figure

2-a illustrates. In MDAG, a similar idea is proposed.

In Figure 2-b, path b

is a single path and c

used as both base and aggregated node. Both Star

and MDAG approaches avoid the creation of new

nodes to represent the aggregations derived from

single paths.

In general, MDAG is 25-35% faster than Star,

consuming, on average, 50% less memory to

represent the same data cube.

3 p-MDAG APPROACH

The p-MDAG approach adopts the

producer/consumer model to minimize

synchronizations. Figure 3 illustrates the logical

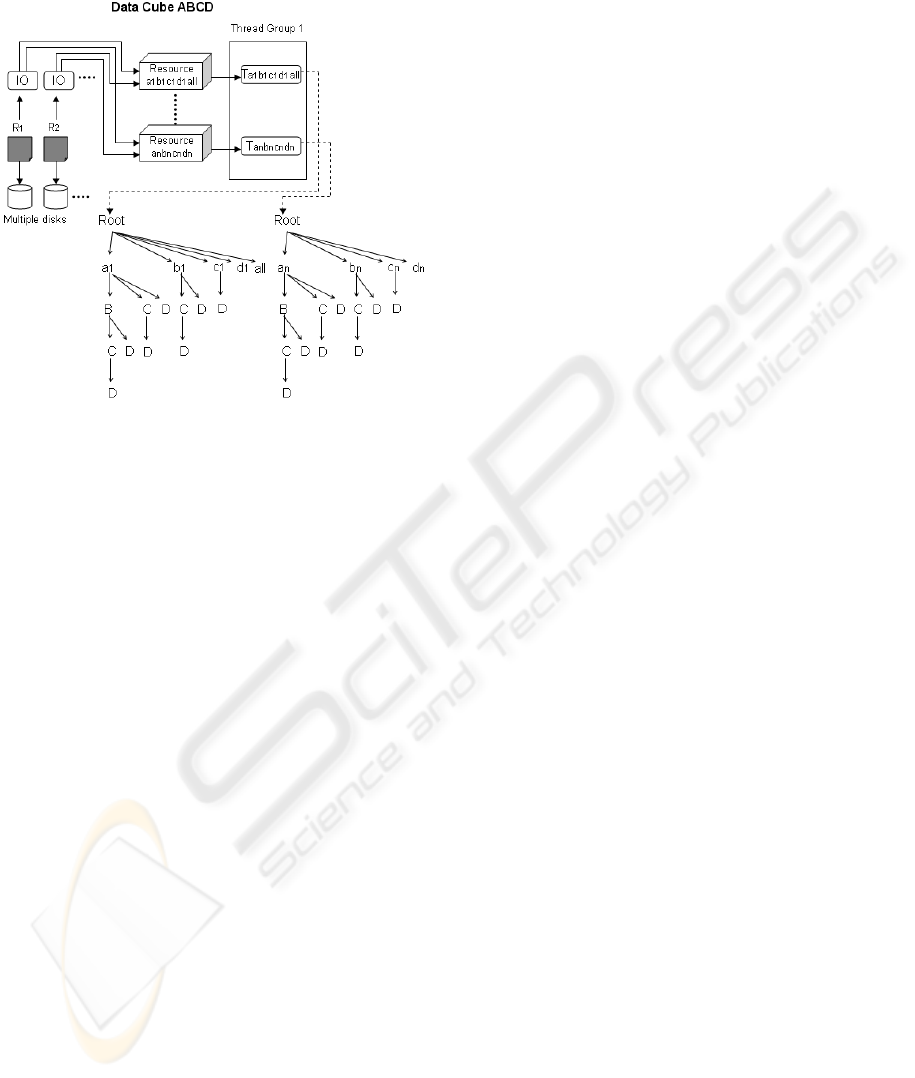
design of p-MDAG approach. A 4D data cube

ABCD is used to exemplify our approach. Each

dimension has equal cardinality n to facilitate the

explanation.

The original base relation R can be partitioned

according to the number of disks and processors. R

can be partitioned into R

, R

, …, R

where

RRRR  ...



. Each R

, R

, …, R

, base

relation represents a subset of R without any

arrangement, i.e., the original R tuples order is

maintained in R

, R

, …, R

base relations. These

independent relations are stored into independent

disks, being read simultaneously by IO threads. Each

independent relation has its own IO thread. The IO

threads implement the producer in the

producer/consumer model. They share the resources

where the tuples are inserted. The unique

synchronization point of the entire solution is the

resource, i.e., the resource access methods putTuple

and getTuple.

The IO threads have the information where each

tuple must be inserted. The criterion for

classification is based on the first dimension

attribute values. In our example, dimension A

attribute values are selected. In the MDAG

sequential approach, one dimension (the highest

cardinality dimension) is used to produce the

internal nodes. If dimension A is selected to form

such internal nodes, the dimension B attribute values

become the criteria for classification. In general, it is

easy to adequate our logical design to a cube compu-

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

324

tation algorithm.

Figure 3: p-MDAG logical design.

Figure 3 illustrates the creation of one resource

per attribute value of dimension A. The same

criterion occurs to the number of threads in groups 1

and 2. The 1-1 relationship is used to facilitate the

explanation. The number of IO threads is

proportional to both number of disks and processors.

The number of resources and threads in group 1 and

2 are proportional to the number of processors. As

mentioned before, the number of attribute values

that each thread of each group is associated depends

on the frequency of each attribute value in the base

relation.

We use Figure 3 to simulate a complete example

execution. We use a tuple t:a

in our

execution. First, t must be stored in one file.

Suppose it is stored in R

. The IO thread associated

to R

loads t and decides which resource t must be

inserted. In our example, t is inserted in resource

After t insertion, one thread of group 1 is notified,

indicating that there is a resource to be consumed.

The threads of group 1 implement the consumer of

the producer/consumer model.

In our example, thread T

is notified. It inserts t

on its cube partition. After t insertion, T

tries to

obtain more tuples from its resource. If there is no

tuple, the thread waits until a notification occurs.

This step continues until there is no more tuples to

be loaded from the disks. The IO threads indicate the

resources when such a condition occurs.

To complete the explanation, we consider t as the

last tuple to be inserted. After T

inserts t on its

partition, it verifies that there is no more tuples to be

inserted in the resource and starts the generation of

the aggregations which begins with a

. In our

example, a

, a

and a

cells are created.

Note that, the remaining aggregated cells a

, a

and a

have being created during the base cuboid

construction.

After the thread group 1 execution, the thread

group 2 starts its execution. To continue the

explanation, we consider thread T

the last thread

that finishes the generation of the aggregations.

After T

execution, the threads T

b1c1d1all

, T

b2c2d2

, …

bncndn

start. The thread T

b1c1d1all

scans the cube

partitions generated previously by thread group 1,

identifying sub-structures that begin with b

, c

and

. These sub-structures are copied to a new cube

partition, maintained by T

b1c1d1all

. The all node are

updated with the measure values of nodes a

… a

during the same scan. The result is another part of a

data cube, composed by cells b

, c

, d

, b

and all.

Assuming that thread T

b1c1d1all

is the last thread

that completes the generation of the remaining

aggregations, after its execution, the full data cube is

complete, as Figure 3 illustrates.

3.1 Architectures

The abstractions, such as IO thread, resource,

threads of group 1 and 2 can be configured in any

architecture. Suppose a shared-memory

multiprocessor architecture with multiple disks. In

such architecture, we instantiate IO threads

according to the number of disks and threads of

group 1 according to the total number of processors

minus the used to IO (suppose there are sufficient

processors for IO and group 1). Since the group 2

threads run after IO and group 1 threads, the number

of threads of group 2 can be equal the total number

of processors. Each thread of group 1 and 2 are

associated with different number of attribute values,

but there is no restriction to this configuration. If the

attribute values are combined according to their

frequencies, the system scales well if we consider

the hardware limitations described before.

In distributed-memory architecture each

processing node can store a part of the base relation,

one IO thread, one resource, one thread of group 1

and one of group 2. Each thread of group 1 shares a

resource with one IO thread and the group 2 threads

must scan all partitions manipulated by group 1

threads. Due to these observations, in a distributed

implementation both resources and cube partitions

manipulated by group 1 must enable remote access.

The remaining producer/consumer ideas can be used

without change.

If each processing node is a multiprocessor

machine with multiple disks, a similar shared-

memory solution can be proposed to each processing

p-MDAG - A Parallel MDAG Approach

325

node. The producer/consumer model modifications

also occur to enable remote access to some

abstractions of p-MDAG approach.

Due to the limited space in this paper, we

compute only full cubes. We run the p-MDAG

approach in a shared-memory multiprocessor

machine with multiple disks. In Section 4, we

discuss some p-MDAG extensions to both compute

iceberg cubes and run p-MDAG in distributed-

memory or hybrid architectures. In the next section,

we describe the main algorithms of p-MDAG

approach.

3.2 Algorithms

In this section, we describe some algorithms of p-

MDAG approach. The IO thread and resource

algorithms are not detailed due to they simplicity.

The first algorithm reads a flat file tuple-by-tuple,

inserting each tuple in a resource. The second

algorithm maintains a collection of tuples, enabling

to insert or remove tuples from it. Each insertion

causes a notification and if the collection of tuples is

empty the resource waits until a new insertion

occurs.

The thread group 1 algorithm is described as

follows:

Algorithm 1 Group 1

Input: A resource Ri

Output: A cube partition

Call Group1();

procedure Group1(){

var: resource Ri;

1: while(Ri has tuples or Ri is not

finished) do{

2: tuple t ← one Ri tuple;

3: measure m ← t measure;

4: traverse the partition creating

new nodes or updating nodes measure,

according to t attribute values;

5: Node l ← leaf node of the

traversal;

6: insert or update l internal node,

using t and m;}//end while

7: Node n ← root node of the partition;

8: for (Node d : n descendants)

9: call mdagAggreg(null, d);}

Lines 2-5 of procedure Group1 generate part of

the base cuboid from the tuples inserted in R

. One

dimension is used to form the internal nodes, so the

respective t attribute value and m measure are used

to create such an internal node (line 6). One of the

main advantages of MDAG approach is to share

internal nodes among non internal nodes. The

internal node sharing method is summarized by line

6. A detailed description of how internal nodes can

be shared is found in (Lima, 2007).

After generating part of the base cuboid, the

aggregation process starts. The aggregations must be

rooted by the attribute value(s) selected to form the

partitions. For example, in Figure 3 the aggregations

generated by thread group 1 must be rooted by a

the first partition, a

in the second, and so on. In

Group1 procedure (lines 7-9), we generate the

aggregations of one partition. For each descendant

of the partition root node a mdagAggreg procedure

call is made. In Figure 3, for each B attribute value a

mdagAggreg call occurs, resulting in a

BD, a

and a

D cells of cuboids ABD, ACD and AD,

respectively. The second partition produces a second

set of cells of ABD, ACD and AD, and so on. The

mdagAggreg procedure is described in (Lima, 2007).

It is important to stress that the direct

aggregation method, proposed in (Lima, 2007), can

also be used by Group1 procedure to avoid the

creation of some aggregated nodes. The direct

aggregation method is an alternative to the single

path compression method, proposed in (Xin, 2007).

The direct aggregation method maintains the single

path nodes with no new nodes to represent their

aggregations. The presence of such single path

nodes guarantees the group 2 partitions integrity,

since a single descendant node in group 1 partition

can become a multiple descendant node in group 2

partition.

The thread group 2 algorithm is described as

follows:

Algorithm 2 Group 2

Input: Partitions of group 1

Output: A cube partition

For (partition f: partitions of group

Call Group2(f root);

procedure Group2(Node n){

var map of attribute values M;

1: for (Node d: n descendants)

2: for (Node d’: d descendants)

3: if (M contains d’ attribute

value) copy d’, including d’ sub-

structure, to the current partition;}

The procedure Group2 scans all partitions

generated by group 1 and copies them to its

partition. The copy is filtered by the attribute values

contained in a map. Only sub-structures rooted by

attribute values contained in such a map are copied.

The map is generated by a main application which

executes a sampling algorithm to identify the

attribute values approximate frequencies. The

investigation of the best sampling techniques is out

of the scope of this work. In p-MDAG, we

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

326

implement a version of the simple random sampling,

proposed in (Olken, 1990).

The main application also starts the IO threads,

group 1 and 2 threads. It controls the start of thread

group 2 after the last thread of group 1 has finished.

In this section, we present the main algorithms

contained in p-MDAG approach. The algorithms

guarantee a unique point of synchronization. Only

the simple getTuple and putTuple methods of the

resource are synchronized. Moreover, the attribute-

based data cube decomposition strategy gives

flexibility to specify the number of threads

according to the hardware. In the next section, we

present the p-MDAG approach performance

analysis.

3.3 Performance Analysis

A comprehensive performance study is conducted to

check the efficiency and the scalability of the

proposed algorithms. All the algorithms are coded in

Java 64 bits (JRE 6.0 update 7). We run the

algorithms in a dual Intel Xeon E5405 with 16GB of

RAM. Each Intel Xeon E5405 is a quad-core

processor, so we have a total of 8 processors (2 GHz

each) in the machine. The 16GB of RAM is shared

among the 8 processors. There are 4 SATAII disks

(7200rpm). The system runs Windows Server 2003

R2 64 bits. All base relations can fit in the main

memory.

For the remaining of this section, D is the

number of dimensions, C the cardinality of each

dimension, T the number of tuples in a base relation,

and S the skew of the data. When S is equal to 0, the

data is uniform; as S increases, the data is more

skewed.

The first set of experiments test all abstractions,

illustrated in Figure 3, running together. We fix the

number of IO threads to two, i.e., each base relation

is divided and stored into two disks. The number of

resources varies from one to six. The number of

threads of group 1 and 2 also varies from one to six.

The number of threads on both groups is always

identical.

The runtimes are compared with respect to the

cardinality (Figure 4), tuple size (Figure 5),

dimension (Figure 6) and skew (Figure 7). In all

scenarios, the runtime decreases almost linear from

experiment with one thread (one thread of group 1

and one of group 2) to two threads (two threads of

group 1 and two of group 2). After two threads, the

runtime decreases slowly, almost stopping after five

threads running simultaneously.

We accomplish an experiment without the IO

threads, i.e., assuming the resources with all tuples

of the base relation. The runtime decreases, but the

curves continue similar, so due to the limited space

we omit the graphics in this paper.

This behaviour is justified by the contention on

the bus system. The cube partitions are shared

nothing, but the architecture is shared-memory. With

one thread, the cube partitions manipulated by group

1 and 2 are created/updated with no concurrence. As

the number of threads increases, the number of

simultaneous operations also increases and the bus

system becomes the bottleneck of the execution.

To prove our assumption that the bus system

becomes the bottleneck of the execution, we run

only one thread per time, collecting the worst time

of thread group 1 and 2. We consider all tuples in

their resources. We instantiate all threads to consider

the main application controls in our results. In

Figure 8, we present the result when computing a

base relation with 8 dimensions, cardinality 10 on

each dimension, skew 0 and 1M tuples. In Figure 9,

we present the result when computing a base relation

with 6 dimensions, cardinality 100 on each

dimension, skew 1.5 and 1M tuples. Due to the

similarity in the results, we omit the graphics where

we change the cardinality and number of tuples.

The speedup, illustrated in Figures 8 and 9, is

one of the key metrics for the evaluation of parallel

database systems (DeWitt, 1992). It indicates the

degree to which adding processors decreases the

runtime. In our context, the relative speedup for p

threads is defined as S

=RT

/RT

, where RT

is the

runtime with one thread and RT

is the runtime with

p threads. An ideal S

is equal to p. That is, the curve

of an ideal S

is a linear diagonal line.

Figures 8 and 9 illustrate an almost linear curve

for p-MDAG approach. There are some points in the

curve where the p-MDAG runtime is bellow the

linear. The attribute-based data cube decomposition

strategy associates a set of attribute values to group

1 and 2. Sometimes, each thread is associated to

more attribute values than others. In our example,

when we run three threads one thread of group 1 is

associated to four attribute values and the other two

threads are associated to three attribute values of

dimension A. The same occur to group 2 threads,

i.e., B, C and D cardinalities have no exact division

by three. Besides unbalanced attribute values

association, the skew can be high and the sampling

method can output incorrect approximate

frequencies, as illustrated in Figure 9. The skew

affects the sampling methods results and all other

data cube decomposition strategies of the literature.

p-MDAG - A Parallel MDAG Approach

327

In the second set of experiments, we present the

runtime and memory consumption of each thread of

groups 1 and 2. We use the same base relation with

8 dimensions, cardinality 10 on each dimension,

skew 0 and 1M tuples. Due to the similarity in the

load balance results, we omit the graphics where we

change the skew, cardinality and number of tuples.

Figures 10 and 11 illustrate the runtime when we

increase the number of threads from one to six. In

Figure 12 and 13, we present the memory

consumption for the same experiment.

In Figures 10-13, we consider T11, T12, … T16

threads of group 1 and T21, T22, … T26 threads of

group 2. In general, the p-MDAG has a good load

balance, since group 1 and 2 are not executed

simultaneously. Groups 1 and 2 must be analysed

separately.

In Figure 14, we test the IO thread scalability.

We simulate a base relation with 5 dimensions, skew

0, cardinality 30 on each dimension and 5M tuples.

The base relation is divided into 2, 3 and 4 equal

size files. Each IO thread reads its file and inserts the

tuples in the resources according to the attribute

values of one dimension. In general, the IO threads

scale well, since we have a synchronized point in the

resources and a contention on the bus system to

consider.

123456

threads

runtime (sec)

pMDAG-C100 pMDA G-C80 pMDA G-C60 pMDA G-C40 pMDA G-C20

Figure 4: Cardinality D=5, T=1M, S=0.

123456

threads

runtime (sec)

pMDAG-T5M pMDAG-T4M pMDA G-T3M pMDAG-T2M

Figure 5: Tuples D=5, C=30, S=0.

100

120

123456

threads

runtime (sec)

pMDAG-8D pMDAG-7D pMDAG-6D pMDA G-5D

Figure 6: Dimension C=10, T=1M, S=0.

100

120

140

123456

threads

runtime (sec)

pMDAG-S0.5 pMDAG-S1 pMDA G-S1.5 pMDAG-S2 pMDAG-S2.5

Figure 7: Skew D=6, T=1M, C=100.

123456

threads

speedup

pMDAG linear

Figure 8: p-MDAG dimension speedup.

123456

threads

speedup

pMDAG linear

Figure 9: p-MDAG skew speedup.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

328

T11T21T11T12T21T22T11T12T13T21T22T23T11T12T13T14T21T22T23T24

1 thread 2 threads 3 threads 4 threads

runtime (sec)

Figure 10: Threads runtime from 1-4.

T11T12T13T14T15 T21T22T23T24T25T11T12T13T14T15T16T21T22T23T24T25T26

5 threads 6 threads

runtime (sec)

Figure 11: Threads runtime from 5-6.

100

200

300

400

500

600

T11 T21 T11 T12 T21 T22 T11 T12 T13 T21 T22 T23 T11 T12 T13 T14 T21 T22 T23 T24

1 thread 2 threads 3 threads 4 threads

memo ry ( MB)

Figure 12: Threads memory consumption from 1-4.

100

120

T11 T12 T13 T14 T15 T21 T22 T23 T24 T25 T11 T12 T13 T14 T15 T16 T21 T22 T23 T24 T25 T26

5 threads 6 threads

memo ry ( MB)

Figure 13: Threads memory consumption from 5-6.

024681012

1 disk

2 disks

3 disks

4 disks

IO runtime (sec)

Figure 14: IO threads scalability.

4 DISCUSSION

In this section, we discuss a few issues related to p-

MDAG and point out some research directions.

There is vulnerability in p-MDAG design,

illustrated in Figure 3. The MDAG sequential

approach can compute full or iceberg cubes. Iceberg

cubes cannot be computed efficiently using thread

group 1 and 2. Unfortunately, the hybrid iceberg

computation of MDAG (top-down computation with

bottom-up pruning) cannot prune infrequent nodes

of group 1 partitions, since these infrequent nodes

can become frequent when aggregated in group 2

partitions. An alternative to solve the iceberg cube

problem is illustrated in Figure 15.

In the second design, the resources and the

threads of group are associated to one or more

attribute values of each dimension of a data cube.

We use a simple association a

… a

facilitate the explanation. For each tuple the IO

thread inserts, in the worst case, D different tuples in

D different resources, where D is the number of

dimensions in a data cube. For example, if the

resources are configured using the attribute values of

Figure 15, a tuple a

will demand a

insertion on resource

a1b1c1d1all

, b

insertion on

resource

a2b2c2d2

, c

insertion on resource

a3b3c3d3

and

insertion on resource

a4b4c4d4

. The same example

using the logical design presented in Figure 3

demands one insertion of a

on resource

The original thread group 1 generates part of the

base cuboid during the tuples insertion. Only after

the complete tuples insertion the threads of group 1

start the generation of the aggregations. Using the

logical design illustrated in Figure 14, each thread of

group 1 generates part of both base cuboid and each

aggregated cuboid, i.e., it generates, for example,

BCD, b

CD, c

D and d

cells instead of only

BCD cells.

In summary, each thread of group 1, illustrated in

Figure 15, will demand longer time to insert the

p-MDAG - A Parallel MDAG Approach

329

same number of tuples when compared to each

thread of group 1, illustrated in Figure 3.

Figure 15: p-MDAG logical design II.

On the other hand, after the base and some

aggregated cuboids generation by thread group 1,

the same group can perform the generation of the

remaining aggregations, pruning infrequent nodes

efficiently, as (Lima, 2007) (Xin, 2007) do

sequentially. The all node can be generated by one

of the resources. After a tuple insertion in the

resource the IO thread also updates the all node in

the same resource. After the last tuple insertion in

the last file, a specific thread is notified to insert the

all node on its cube partition.

The logical design illustrated in Figure 15

increases the number of tuples on each resource and

the number of initial insertions of thread group 1, so

it must be studied carefully.

The advantage of a distributed-memory or

shared-nothing architecture is that accesses to local

data can be quite fast. On the other hand, accesses to

remote memories require much more effort. In

general, data placement is important to reduce the

number of data references, since any data reference

requires communication. (Dongarra, 2003)

The logical design proposed in Figure 3 requires

remote access to resources and partitions

manipulated by thread group 1. Each partition can

have million of nodes and each thread of group 2

must scan all partitions of group 1, so there is a

communication overhead. The logical design,

illustrated in Figure 15, requires remote access to

resources only, but additional tuples can increase the

communication overhead. In summary, we have to

accomplish some experiments with different

architectures and both logical designs presented in

this paper, since distributed-memory architecture

introduces communication overhead and shared-

memory architecture introduces contentions on the

bus system.

The utilization of secondary memory is another

aspect to be considered. Parallel approaches partition

the data cubes. Each partition can be stored to disk,

enabling one partition per time in main memory.

One may also consider the case that even a specific

partition may not fit in memory. For this situation,

occurred specially in distributed-memory

architectures where each processing node has only

one cube partition, the projection-based pre-

processing, proposed in (Han, 2001), can be an

interesting solution.

Finally, we must consider how queries can be

designed. We believe that any cube query method,

including iceberg, top-k, point, inquired and rank

query methods, can be easily integrated with p-

MDAG approach.

5 CONCLUSIONS

In this paper, we present a novel parallel cube

computation and representation approach, named p-

MDAG. The p-MDAG approach proposes an

attribute-based data cube decomposition strategy

which combines both task and data parallelism. The

p-MDAG approach uses the dimensions attribute

values to partition the data cube. It also redesigns the

two phase (base and aggregation phases) MDAG

sequential algorithms to run in parallel. In general,

p-MDAG approach has both good load balance and

similar memory consumption among its threads, as

our experiments demonstrate. Its logical design can

be implemented in shared-memory, distributed-

memory and hybrid architectures with minimal

adaptation.

The logical design has vulnerability in

computing iceberg-cubes. We propose an alternative

design to solve the problem. The iceberg logical

design, illustrated in Figure 15, must be tested in

shared-memory architecture. Moreover, both designs

must be tested in distributed-memory and hybrid

architectures. Finally, an interesting study is the

development of some extensions to enable p-MDAG

to use efficiently secondary memory during the cube

computation.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

330

REFERENCES

Beyer, K. and Ramakrishnan, R. Bottom-up computation

of sparse and Iceberg CUBEs. SIGMOD, 28(2):359–

371, 1999.

Chen, Y., Dehne, F., Eavis, T. and Rau-Chaplin, A.

Parallel ROLAP data cube construction on shared-

nothing multiprocessors. Distributed and Parallel

Databases, 15:219-236, 2004.

Chen, Y., Dehne, F., Eavis, T. and Rau-Chaplin, A. PnP:

sequential, external memory, and parallel iceberg

cube computation. Distributed and Parallel Databases,

23(2):99-126, 2008.

Dehne, F., Eavis, T., and Rau-Chaplin, A. Parallelizing

the data cube. Distributed and Parallel Databases,

11(2):181-201, 2002.

Dehne, F., Eavis, T., Hambrush, S. and Rau-Chaplin, A.

Parallelizing the data cube. International Conference

on Database Theory, 2001.

DeWitt, D. and Gray, J. Parallel database systems: the

future of high performance database systems.

Communications of the ACM, 35(6):85-98, 1992.

Dongarra, J., Foster, I., Fox, G., Gropp, W., Kennedy, K.,

Torczon, L. and White, A. Source Book of Parallel

Computing. Morgan Kaufman, 2003.

Goil, S. and Choudhary, A. High performance OLAP and

data mining on parallel computers. Journal of Data

Mining and Knowledge Discovery, (4), 1997.

Goil, S. and Choudhary, A. High performance

multidimensional analysis of large datasets. First

ACM International Workshop on Data Warehousing

and OLAP, pages 34-39, 1998.

Goil, S. and Choudhary, A. A parallel scalable

infrastructure for OLAP and data mining.

International Database Engineering and Application

Symposium, pages 178-186, 1999.

Gray, J., Chaudhuri, S., Bosworth, A., Layman, A.,

Reichart, D., Venkatrao, M., Pellow, F. and Pirahesh,

H. Data cube: A relational aggregation operator

generalizing group-by, cross-tab, and sub totals. Data

Mining and Knowledge Discover, 1(1):29–53, 1997.

Han, J., Pei, J., Dong, G. and Wang, K. Efficient

computation of iceberg cubes with complex measures.

SIGMOD, pages 1–12. ACM, 2001.

Han, J., Kamber, M. Data Mining Concepts and

Techniques. Morgan Kaufman, 2006.

Lakshmanan, L.V.S., Pei, J. and Han, J. Quotient cube:

How to summarize the semantics of a data cube.

VLDB’02, pages 778–789. Morgan Kaufmann, 2002.

Lima, J.C. and Hirata, C.M. MDAG-Cubing: A Reduced

Star-Cubing Approach. SBBD, 362-376, October

2007.

Lu, H., Yu, J., Feng, L. and Li, X. Fully dynamic

partitioning: Handling data skew in parallel data cube

computation. Distributed and Parallel Databases,

13:181-202, 2003.

Li, X., Han, J. and Gonzalez, H. High-dimensional OLAP:

A minimal cubing approach. In VLDB’04, pages 528–

539. Morgan Kaufmann, 2004.

Muto, S. and Kitsuregawa, M. A dynamic load balancing

strategy for parallel data cube computation. ACM 2

Annual Workshop on Data Warehousing and OLAP,

pages 67-72, 1999.

Olken, F., and Rotem, D. Random sampling from database

files - a survey. In 5th International Conference on

Statistical and Scientific Database Management, 1990.

Xin, D., Han, J., Li, X. and Wah, B.W. Star-Cubing:

Computing Iceberg Cubes by Top-Down and Bottom-

Up Integration. VLDB’03, pages 476-487. Morgan

Kaufmann, 2003.

Xin, D., Han, J., Li, X., Shao, Z. and Wah, B.W.

Computing Iceberg Cubes by Top-Down and Bottom-

Up Integration: The StarCubing Approach. IEEE

Transactions on Knowledge and Data Engineering,

19(1): 111-126, 2007.

Xin, D., Shao, Z., Han, J., and Liu, H. C-cubing: Efficient

computation of closed cubes by aggregation-based

checking. ICDE’06, page 4. IEEE Computer Society,

2006.

Zhao, Y., Deshpande, P., and Naughton, J. F. An array-

based algorithm for simultaneous multidimensional

aggregates. SIGMOD, pages 159–170. ACM, 1997.

p-MDAG - A Parallel MDAG Approach

331