THE CHEMNITZ HYBRID EVOLUTIONARY

OPTIMIZATION SYSTEM

Ulf Nieländer

Chemnitz University of Technology, Computer Science Department, Modelling & Simulation Group

09107 Chemnitz, Germany

Keywords: Genetic algorithms, Single

objective

Multi

objective optimization, CHEOPS, Omni Optimizer, Bench-

marking, Test functions.

Abstract: This paper introduces the Chemnitz Hybrid Evolutionary Optimization System to the scientific community.

CHEOPS is a non

standard, high

performance genetic algorithm framework allowing simple as well as

advanced modes of operation. Universal genetic algorithms well

suited for solving both single

and multi

objective optimization problems are still a matter of serious research. The Omni Optimizer was a milestone

that

research

topic,

but

now

dramatically

outperformed

CHEOPS

single

objective

optimization.

The comparison should soon continue, because CHEOPS will be straightforwardly enhanced to solve multi

objective problems as well.

1 INTRODUCTION

This paper introduces the Chemnitz Hybrid Evolu-

tionary Optimization System to the scientific com-

munity. Being developed as an Eng.

D. project, it is

described in full detail by Nieländer (2009). Basical-

ly, CHEOPS is a non

standard, high

performance

genetic algorithm framework. However, CHEOPS is

still under construction. That is why the author

presents only single

objective optimization results

in the present paper, whereas CHEOPS will be

straightforwardly enhanced to solve multi

objective

problems as well. Omni Optimization, i.

e. using a

single algorithm for successfully and efficiently

solving different kinds of optimization problems

often encountered in practice, is a relevant research

topic. It has been coined by Deb and Tiwari (2005,

2008) in their pioneering papers. Therein they have

proposed the (extended) Omni Optimizer. However,

its single

objective optimization performance does

indeed cause serious doubts.

After this introduction, Section 2 presents and

discusses the basic features of CHEOPS. These

include representational issues, genetic operators,

selection methods, the cyclic mode of operation, and

the generational concept. Section 3 gives a brief out-

line of the opponent for the following comparison,

e. the Omni Optimizer proposed by Deb and Tiwa-

ri (2005, 2008). Afterwards, the comparison between

the two GA is executed and assessed in Section 4.

running the original benchmark tests now, CHE-

OPS outperforms the Omni Optimizer dramatically.

Section 5 discusses advanced modes of operation of

CHEOPS, whereas Section 6 points out to future

work of straightforwardly enhancing CHEOPS to

solve multi

objective problems as well. Finally,

Section 7 concludes the paper with a short summary.

2 THE BASIC FEATURES

OF CHEOPS

When developing and implementing an evolutionary

algorithm, the programmer has to think about five

major subjects:

How to represent candidate solutions and how to

arrange them in a population? How to produce new

candidate solutions from existing ones? How to

select preferably good and

or rather bad candidate

solutions from the population? How does it work

altogether in some optimization cycle? How to pro-

ceed to the next generation?

All these issues will be discussed in the follow-

ing subsections.

311

Nieländer U..

THE CHEMNITZ HYBRID EVOLUTIONARY OPTIMIZATION SYSTEM .

DOI: 10.5220/0003059203110320

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 311-320

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

2.1 Representation of Candidate

Solutions

Originally, genetic algorithms have just used binary

chromosomes especially with Gray coding of all the

variables of the current optimization problem. Such

binary chromosomes can be used in CHEOPS that

are built

up from a sequence of bits. Evolution

strategies, however, have always used floating

point

chromosomes (i.

e. vectors of real numbers) being

much more suitable for real

parameter optimization.

Likewise, integer chromosomes are appropriate for

integer

parameter

optimization.

Moreover,

CHEOPS

handles permutation chromosomes for combinatorial

optimization solving e.

g. the famous traveling sales-

man problem.

For all the chromosome types there is an initiali-

zation procedure (random uniform sampling within

the search space) built into CHEOPS. A population

is just a large, panmictic set containing such indi-

viduals as current candidate solutions.

2.2 Genetic Operators

Remember the default mode of operation of genetic

algorithms: Two previously selected parent indi-

viduals are recombined with the offspring being

slightly modified afterwards to obtain some child

individuals. Thus, recombination

crossover is pri-

mary, whereas modification

mutation is secondary.

Quite the contrary applies to evolution strategies.

In nature, however, some species alternate the

way they reproduce themselves from one generation

to the next (agamogenesis vs. sexual reproduction),

whereas other creatures perform metagenesis to

survive the struggle for life. CHEOPS adapts this by

implementing a variety of genetic reproduction

operators for each chromosome type. In the context

of the present paper, only genetic operators for

floating

point chromosomes are relevant:

 one

point crossover (biased

shuffled);

 two

points crossover;

 uniform crossover;

 generalized linear crossover (standard

mixed);

 BLX crossover;

 intermediate crossover (standard

/ arithmetical

mixed);

 shifting mutation (standard

reversed);

 universal mutation (just copy, or uniform

mutation, or boundary mutation, or average

mutation, or Gaussian mutation, or Breeder

mutation as well as mixed).

All these genetic operators implemented in CHE-

OPS are well

known from GA literature. That is

why the author does not go into detail here but refers

to Nieländer (2009) for further explanations.

Unlike the default mode of operation of genetic

algorithms and evolution strategies, CHEOPS does

not distinguish between primary and secondary

operators. Consequently, each such genetic operator

is just a procedure that takes some parent indi-

vidual(s) and produces some child individual(s).

How it actually does its job

by a mutation of one

parent individual or by crossover from two parent

individuals, and in doing so directly inspired by

genetics or otherwise by some heuristics or even

with another local or global optimization procedure

built into (i.

e. hybrid optimization)

is completely

irrelevant. Please note that arbitrary such genetic

operators can be implemented in CHEOPS by the

user as desired and

or required.

2.3 Selection Methods

The following selection methods are implemented in

CHEOPS for single

objective optimization:

 unbiased roulette selection;

 ranking selection (linear

exponential);

 threshold uniform selection;

 tournament selection (first

better

all

best).

Again, these selection methods are very common

in genetic algorithms and do not need further ex-

planations here (see Nieländer, 2009, again). They

are implemented in CHEOPS both ways, selecting

preferably good candidate solutions to reproduce

and rather bad ones to die. Moreover, CHEOPS

handles maximization as well as minimization prob-

lems without requiring the user to re

formulate them

prior to optimization. Thus, selecting a candidate

solution directly depends on how good or bad it

solves the current optimization problem compared to

all other individuals within the current population.

Please note that CHEOPS does not restrict selection.

Thus, at least in principle, each candidate solution

within the population may have a chance to repro-

duce and

or to die. That is why elitism is separately

keeping track of the best candidate solution(s) found

so far while the genetic algorithm is running.

2.4 Cyclic Mode of Operation

The successive sequence of what genetic operator

when produces new children is not predetermined.

This is due to chance in the randomized evolution

process. Of course, each genetic operator knows

how many parent individuals it needs to do its job.

Thus, so many candidate solutions will be selected

from the current population each by one of the

several selection methods implemented in CHEOPS.

ICEC 2010 - International Conference on Evolutionary Computation

312

What follows is the CHEOPS optimization cycle

pseudo

code:

Generate the initial population

using random uniform sampling

Repeat

Randomly choose one of the

genetic operators to apply next

Repeat

Randomly choose one of the

selection methods and select

(according to the current

optimization direction) an

individual from the population

to reproduce

Until all necessary parent indi-

viduals have been selected

Apply that genetic operator

producing child(ren) from the

parent(s)

Repeat

Randomly choose one of the

selection methods and select

(contrary to the current

optimization direction) an

individual from the population

to die

Replace that individual by

a child just produced

Until all the child individuals

have been assimilated into

the population

Until some stopping criterion is met

Someone might argue that this is too simple to

work well. Note, however, that CHEOPS does also

allow advanced and elaborated modes of operation

(see Section 5 for details). In the context of the

present paper, due to the reminder of De Jong (2006,

p. 3), we intentionally “‘Keep it simple, stupid!’

which turns out to be a surprisingly useful heuristic

for building evolutionary systems that we have some

hope of understanding!”

2.5 Steady State Concept

Resulting from the aside pseudo

code, good candi-

date solutions must first be selected as parents for

reproduction, and their children then replace bad

candidate solutions within the population (not allow-

ing a duplicate solution to be inserted). That is the

concept of a steady state genetic algorithm.

The main advantage of steady state genetic algo-

rithms is, that any good candidate solution produced

in the evolution process can immediately be selected

as parent individual for reproducing and hopefully

breeding still better child individual(s). Usually, this

speeds up the evolution process enormously com-

pared to generational genetic algorithms. Those fill

up some intermediate population and

or the next

generation with child individuals all of them being

produced from old parent individuals.

However, there is a drawback with steady state

genetic algorithms: inbreeding. Any especially good,

but maybe just locally optimal candidate solution

might be selected as parent again and again, thus

forcing too much exploitation over exploration and

continuously producing children related and possibly

similar to each other. Thus, it is essential for a

steady state genetic algorithm to implement some

counter

forces against inbreeding. That is why

CHEOPS simultaneously uses many different se-

lection methods as well as genetic operators. Hence,

the selective pressure varies and the genetic diversity

within the population is long

term maintained: Even

if the same parent individuals are being selected,

different child individuals will usually be produced

from them.

CHEOPS’ main control parameter setting a good

balance between exploitation and exploration is the

population size counting the number of candidate

solutions therein. Of course, a smaller population

favors exploitation over exploration

vice versa for

a larger population. Thus, optimization performance

depends on the population size as Section 4 reveals.

3 THE OMNI OPTIMIZER

Prior to 2005, single

and multi

objective problems

as well as uni

optimal or multi

optima problems

have usually been dealt with different optimization

algorithms. Then, in their pioneering paper, Deb and

Tiwari (2005) have proposed an unique approach for

solving different kinds of function optimization

problems often encountered in practice. They have

introduced the Omni Optimizer to the scientific

community and, as far as the author knows, it was

the first genetic algorithm that can automatically

adapt to solving those problems in a single opti-

mization run. This idea has immediately spread out

(see Coelho and Von Zuben, 2006, Klanac and

Jelovica, 2007, for example). Later, Deb and Tiwari

(2008) have published their extended Omni Opti-

mizer: “In this paper, for the first time, we suggest

an omni

optimizer, in which a single optimization

algorithm attempts to find one or more near

optimal

solutions for the following four types of optimization

problems [single

or multi

objective problems and

uni

optimal or multi

optima problems] in a single

simulation run of the algorithm ” (p. 1064).

THE CHEMNITZ HYBRID EVOLUTIONARY OPTIMIZATION SYSTEM

313

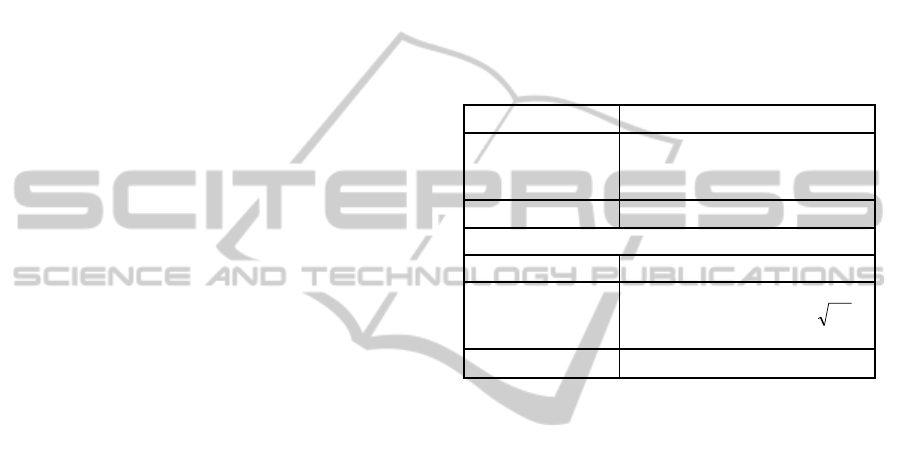
Let us present a brief outline of their proposed

Omni Optimizer. It is a generational genetic algo-

rithm that makes use of Latin

hypercube sampling

to generate its initial population. Simulated binary

crossover followed by polynomial mutation are

being used to produce two child individuals from

two parent individuals. Basically, the Omni Opti-

mizer works similar to the well

known fast and

elitist Non

dominated Sorting Genetic Algorithm

NSGA

II (see Deb, Pratap, Agarwal and Meyarivan,

2000, 2002) with some improvements resulting from

restricted selection and a more disruptive mutation

operator. Thus, excellent multi

objective optimi-

zation performance is out of question as confirmed

for the NSGA

II by many qualified studies.

However, if just one objective function is pre-

sent, the Omni Optimizer automatically “degener-

ates” (Deb and Tiwari really call it that way) and

adapts itself to solving the current single

objective

optimization problem efficiently. Here, a tournament

selection method is used with just two candidate

solutions taking part.

We refer to Deb and Tiwari (2005, 2008) them-

selves for a detailed description of the Omni Opti-

mizer and its extended version including pseudo

code.

4 COMPARISON

BETWEEN CHEOPS AND THE

OMNI OPTIMIZER

Definitely, the Omni Optimizer is a milestone in that

research topic, but does its extended version also

mark the end of the road? In this section we discuss

the single

objective optimization performance of the

(extended) Omni Optimizer comparing it with

CHEOPS re

running the original benchmark tests

now. Let us see whether simple CHEOPS in its basic

mode of operation can challenge the Omni

Optimizer successfully or not.

4.1 First Round of the Comparison:

Single

Objective Optimization

Results

To assess the efficiency of their proposed Omni Op-

timizer algorithm for single

objective optimization,

Deb and Tiwari (2005) present results of two bench-

mark functions only. Both functions are taken from

GA literature: the 20-variable Rastrigin function and

the 20-variable Schwefel function are well

known.

Table 1 reprints the functions’ definitions of Deb

and Tiwari. They claim that both functions have

many local minima, but there is only one global

minimum

= 0.0. Note, however, that this is a mis-

take for the Schwefel function: Using 418.9829 ⋅ n,

as Deb and Tiwari did, zero cannot be achieved as

the global minimum. Instead,

= 0.000012727566

2937252135648043992913093849 ⋅ n results for the

Schwefel function. Anyway, to be comparable with

their results we use those definitions of Deb and

Tiwari as reprinted in Table 1 throughout the present

paper.

Table 1: Definitions of the two test functions according to

Deb and Tiwari (2005, 2008).

Test function Rastrigin

=)(xf

(

)

∑

⋅π⋅−⋅+

))2(cos1(10

Variables’ range

−

10 ≤ x

≤ 10

Test function Schwefel

)(xf

∑

⋅−⋅

xxn

||sin9829.418

Variables’ range

−

500 ≤ x

≤ 500

The population size

counting the number of

candidate solutions therein

is an essential control

parameter of any genetic algorithm to set a good

balance between exploitation and exploration. Thus,

optimization performance depends on the population

size, but Deb and Tiwari do not explain whether

they set it arbitrary or intentionally. Using a popu-

lation size of 20 individuals (for the 20-variable

Rastrigin function) respectively 50 individuals (for

the 20-variable Schwefel function), they execute

some optimization runs and present the best, median,

and worst number of objective function evaluations

required by their Omni Optimizer to achieve and

fall below

= 0.01. However, it is hardly compre-

hensible why such a rough approximation solely

determines their performance criterion? Any

advanced optimization tool should quickly achieve

and fall below that predefined threshold value,

because such an (in-)

accuracy of the approximation

is only worth a low grade 4 of merit according to

Schwefel (1975, 1995) himself. Afterwards,

convergence to the true global minimum is often a

difficult job and much more challenging, because it

requires very fine tuning of all the x

variables.

To assess the optimization performance of the

extended Omni Optimizer, both the Rastrigin func-

tion and the Schwefel function are again used by

ICEC 2010 - International Conference on Evolutionary Computation

314

Table 2: Single

objective optimization results for the Rastrigin function.

Omni Opt CHEOPS Ext Omni Opt CHEOPS Ext Omni Opt CHEOPS

Test function

Rastrigin (n = 20 variables) Rastrigin (n

20 variables) Rastrigin (n = 10 variables)

Population size

20 40 40

Best run

260 2

369 24 520 2 570 8 120 1

588

Median

660 3

206 41 760 4 250 15 520 2

336

Worst run

120 5

419 106 440 6 730 53 480 3

117

objective function evaluations until f

0.01

Table 3: Single

objective optimization results for the Schwefel function.

Omni Opt CHEOPS Ext Omni Opt CHEOPS Ext Omni Opt CHEOPS

Test function Schwefel (n = 20 variables) Schwefel (n = 20 variables) Schwefel (n = 10 variables)

Population size 50 16 16

Best run 54

950 3

348 26

128 2

075 6

304 1

244

Median 69

650 4

290 36

272 3

235 11

360 1

814

Worst run 103

350 6

069 82

096 4

607 24

704 2

513

objective function evaluations until

< 0.01

Deb and Tiwari in their second paper (2008) as

single

objective, uni

optimal benchmark functions

(but now with 10 and 20 variables). They execute

some optimization runs

unlike before now with

different population size(s) without giving the

reason for that. Again, they present the best, median,

and worst number of objective function evaluations

required by the extended Omni Optimizer to achieve

and fall below

= 0.01 as predefined threshold

value.

Tables 2 and 3 compare the results of the Omni

Optimizer and its extended version with the results

of CHEOPS. Setting the same population size(s), the

(extended) Omni Optimizer is dramatically out-

performed, because CHEOPS is much more resolute

and faster when optimizing. Its worst runs required

only fractions of the objective function evaluations

of the best Omni Optimizer runs. Remember that

CHEOPS just uses random uniform sampling to

generate its initial population, whereas the Omni

Optimizer makes use of Latin

hypercube sampling

in all its runs. Due to such a jump start, the poor

performance of the Omni Optimizer and its extended

version is disappointing. Sometimes its runs have

really been long

term requiring a huge number of

objective function evaluations to achieve and fall

below that predefined threshold value.

Let us now compare the Ext Omni Opt columns

in Tables 2 and 3 with the corresponding Omni Opt

columns. On the one hand there is a better perform-

ance for the 20-variable Schwefel function; on the

other hand there is a much worse performance for

the 20-variable Rastrigin function. Thus, from that

comparison we cannot draw obvious conclusions

about the extended Omni Optimizer.

Let us also compare the CHEOPS columns in

Tables 2 and 3 for n = 20. CHEOPS runs more effi-

cient in smaller populations keeping only 20 rather

than 40 respectively 16 rather than 50 candidate

solutions. This also indicates that the 20-variable

Rastrigin function and the 20-variable Schwefel

function both are not too difficult to be minimized

until achieving and falling below that predefined

threshold value.

Setting the original population size of 20 indivi-

duals (for the 20-variable Rastrigin function) respec-

tively 50 individuals (for the 20-variable Schwefel

function), let us continue the CHEOPS runs beyond

that predefined threshold value until 19

260 respec-

tively 54

950 objective function evaluations at most.

Remember that the Omni Optimizer for the first time

ever has achieved

< 0.01 at those moments. In all

its runs, CHEOPS has approximated the true global

minimum with a small difference of less than 10

−9

not just at those moments, but thousands of objective

function evaluations earlier. According to the

original grades of merit by Schwefel (1975, 1995)

himself, this is worth a high grade 2. Note that for

the highest grade 1, the approximation to the true

global minimum has to be as precise as 10

−38

. How-

ever, we did not use such an extended floating

point

precision when compiling CHEOPS.

Please note that the Rastrigin function and the

Schwefel function are the only single

objective,

THE CHEMNITZ HYBRID EVOLUTIONARY OPTIMIZATION SYSTEM

315

uni

optimal benchmark functions used by Deb and

Tiwari (2005, 2008) to assess the optimization

performance of the (extended) Omni Optimizer. It

follows from the definitions in Table 1 that both

functions are separable in all of their variables. Each

function can be re

formulated by a sum

∑

xfxf

)()(

of one

dimensional sub

functions. Thus, every x

variable may take its best value (without regard to

the others) to optimize by itself its contribution to

the desired objective function value. Usually, such

separable functions are of low or medium difficulty

for any advanced optimization tool, and they are

rarely coming across in real

world optimization

practice.

4.2 Second Round of the Comparison:

Further Single

Objective

Optimization Results

So far, optimization performance is assessed by how

many objective function evaluations are being

required until achieving and falling below a pre-

defined threshold value. Alternatively, how precise

does the optimization tool approximate the global

minimum within a limited number of objective

function evaluations?

Such tests are furthermore examined by Deb and

Tiwari only in their second paper (2008). They have

collected the objective function value of the best

candidate solution achieved within 10

000 objective

function evaluations at most, and then they have

averaged over 99 executed runs. Unfortunately, they

do not state the population size(s) used in the runs

when collecting their results of the extended Omni

Optimizer. Did it remain constant throughout all the

executed runs, or did it change from one test

function to another (as in the previous tests), or did it

vary for all the test functions with the number of

variables increasing (as not in the previous tests)?

Note that there are now 10 to 100 variables (at steps

of 10). We have opted for the second case in the

corresponding CHEOPS runs, and a population size

of 26 (for the Rastrigin function) respectively 24 (for

the Schwefel function) seem to work well for

n = 100. However, we did not execute numerous

pre

runs to find out the best population size(s) for

all n < 100 specifically. If we had done such tuning,

then we would have opted for the third case, because

the test functions are obviously more difficult to

minimize in high dimensions rather than in low

dimensions. Thus, as a rule of thumb, the population

size may also increase somewhat with increasing n

to achieve the very best optimization performance.

Table 4: Further single

objective optimization results for

the Rastrigin function.

Ext Omni Opt CHEOPS

Test function Rastrigin

Population size

?? 26

n = 10 variables

1.65

⋅

−3

1.071 ⋅ 10

−10

n = 20 variables

1.71

⋅

−2

4.398 ⋅ 10

−6

n = 30 variables

6.71

⋅

−2

6.884 ⋅ 10

−6

n = 40 variables

1.44

⋅

−1

3.520 ⋅ 10

−5

n = 50 variables

2.51

⋅

−1

3.833 ⋅ 10

−3

n = 60 variables

3.75

⋅

−1

2.144 ⋅ 10

−3

n = 70 variables

5.00

⋅

−1

2.979 ⋅ 10

−2

n = 80 variables

6.40

⋅

−1

6.672 ⋅ 10

−2

n = 90 variables

7.85

⋅

−1

4.090 ⋅ 10

−1

n = 100 variables

9.37

⋅

−1

2.195 ⋅ 10

−1

averaged

after 10

000 objective

function evaluations

Note, however, that Deb and Tiwari (2008) have

narrowed the variables’ range for the Rastrigin func-

tion by almost 50

% to −

5.12 ≤ x

≤ 5.12 now with-

out giving the reason for that. It was only recently

noticed by the author when writing this paper. That

is why CHEOPS did run with the original variables’

range −

10 ≤ x

≤ 10 for the Rastrigin function when

collecting the results in the above Table 4.

Remember that the definition of the Schwefel

function by Deb and Tiwari is used throughout this

paper (see Table 1). Thus, its global minimum is not

zero, but ~ 1.273 ⋅ 10

−5

⋅ n instead

which has really

been achieved for n = 10 and n = 20 variables in all

CHEOPS runs within 10

000 objective function

evaluations at most.

Furthermore, Deb and Tiwari (2008) use another ten

single

objective, uni

optimal benchmark functions

(with 10 to 100 variables at steps of 10) and present

results of how precise does the extended Omni

Optimizer approximate their global minimum within

000 objective function evaluations at most.

However, six out of them are again separable in all

of their variables. As mentioned before, such func-

tions are commonly inappropriate for assessing the

performance of optimization tools, because the so

called curse of dimensionality only strikes linearly

with increasing n, rather than exponentially. Thus,

their statement “that the omni

optimizer is ideally

suited for solving large

scale optimization problems

and its performance does not degrade significantly

by increasing the dimension of decision space” (p.

1074) is not sincerely justified. Rather than re

running further tests with only limited significance,

ICEC 2010 - International Conference on Evolutionary Computation

316

Table 5: Further single

objective optimization results for

the Schwefel function.

Ext Omni Opt CHEOPS

Test function Schwefel

Population size

?? 24

n = 10 variables

2.00

⋅

−2

1.273 ⋅ 10

−

n = 20 variables

7.98

⋅

−1

2.546 ⋅ 10

−

n = 30 variables

2.73

⋅

3.846 ⋅ 10

−

n = 40 variables

5.90

⋅

1.397 ⋅ 10

−

n = 50 variables

7.74

⋅

5.747 ⋅ 10

−

n = 60 variables

9.62

⋅

5.847 ⋅ 10

−

n = 70 variables

1.16

⋅

2.654 ⋅ 10

−

n = 80 variables

1.37

⋅

1.231 ⋅ 10

n = 90 variables

1.48

⋅

1.092 ⋅ 10

n = 100 variables

1.63

⋅

1.798 ⋅ 10

averaged f after 10

000 objective function

evaluations

the author refers to the very stringent benchmark

functions for single

objective optimization compiled

by Nieländer (2009), and to the excellent CHEOPS

results presented therein.

5 CHEOPS’ ADVANCED

MODES OF OPERATION

Remember that CHEOPS simultaneously uses many

different selection methods as well as genetic op-

erators in its basic optimization cycle. Hence, the

selective pressure varies and the genetic diversity

within the population is long

term maintained: Even

if the same parent individuals are being selected,

different child individuals will usually be produced

from them.

If some genetic operator turns out to be well

suited for the current optimization problem, because

it frequently or even regularly produces still better

child chromosomes, then it would make sense to ap-

ply it more often

likewise the selection methods

involved. This may speed up the evolution process

and

or increase robustness. Reflecting the evolution

of the population, CHEOPS builds up a dynamic pe-

digree and uses reinforcement learning (systematic

reward and penalty) to adjust the probabilities of

applying each genetic operator and each selection

method adaptively while the algorithm is running.

Note, unfortunately, that this does not suspend the

No Free Lunch theorem of Wolpert and Macready

(1995, p. 24): “It should be noted that this applies

even if one considers ‘adaptive’ search algorithms

which modify their search strategy based on pro-

perties of the population of

[

candidate solution

its

objective function value

]

pairs observed so far in

the search, and which perform this ‘adaptation’

without regard to any knowledge concerning salient

features of

f.”

Someone might argue that simultaneously using

many different selection methods as well as genetic

operators would not be enough against the risk of

inbreeding with steady state genetic algorithms. That

is why further counter

forces for advanced modes of

operation are implemented in CHEOPS:

 After being selected for reproduction, a candi-

date solution may get older by automatically

making its objective function value a little bit

worse. Thus, any especially good, but maybe

just locally optimal candidate solution cannot

determine the evolution process forever.

 Since all the selection methods are imple-

mented both ways, CHEOPS may occasionally

revert the current optimization direction

(maximization vs. minimization) for a short

time to find its way back from local optima not

being stuck therein forever.

 Once in a while, CHEOPS can re

initialize

some good, or bad, or randomly picked candi-

date solutions thus stimulating the evolution

process again by bringing new individuals

(random uniform sampling within the search

space) into the population.

 Multiple populations can evolve simultaneous-

ly in parallel with occasional exchange

migra-

tion of candidate solutions.

When separately or in combination activating

those advanced modes of operation and running,

unfortunately, CHEOPS’ optimization performance

is difficult to analyze both theoretically as well as

systematically. There are many control parameters to

set

up initially, but no obvious relationship between

parametrization and current optimization per-

formance could be established yet. General rules for

automatic optimal, at least reasonable set

up would

be nice to have to avoid numerous pre

runs prior to

actual optimization. Thus, there is a lot of on

going

research on each of these advancements and their

particular usefulness.

6 FUTURE WORK: SOLVING

MULTI

OBJECTIVE

PROBLEMS

Many mathematical, techn(olog)ical, or economic

optimization problems from scientific, industrial,

and commercial practice do not involve just one

objective function. Instead, several objectives have

THE CHEMNITZ HYBRID EVOLUTIONARY OPTIMIZATION SYSTEM

317

to be fulfilled simultaneously. Generally, these

objectives will be independent of each other and

conflicting as well as incommensurable with some

of them to be maximized and the other(s) to be

minimized. However, in a Cost Benefit Analysis for

example, minimum expenses cannot yield maximum

profits due to economic reasons. Hence, a unique

and perfect solution meeting all the objectives’

optimal values does hardly exist. Instead, improve-

ment in one objective can only be achieved by some

other objective’s deterioration. That is why the

requirements to the optimization tools and their

search and solution procedures are more challenging

for multi

objective optimization compared to usual

single

objective optimization.

6.1 Appropriate Selection Methods

In single

objective optimization, all candidate solu-

tions can be compared and sorted according to their

objective function value. The selection methods of

evolutionary algorithms rely on such a comparison

and ranking. In multi

objective optimization, how-

ever, two candidate solutions are incomparable if the

first is better than the second for some objective(s)

whereas the second is better than the first for another

objective(s). Thus, the two candidate solutions do

not dominate each other. Consequently, appropriate

selection methods are particularly necessary for an

evolutionary algorithm not only to handle single

objective optimization problems, but also to tackle

multi

objective optimization problems and to solve

them successfully in a single run. The usual weight-

ed sum approach might not be adequate.

As mentioned before, a unique and perfect solu-

tion meeting all the objectives’ optimal values does

hardly exist. Instead, the optimization tool should

output lots of such candidate solutions that cannot be

dominated by any other(s), thus spanning the trade

off surface for the current optimization problem in

the objective space. That is known as Pareto

optimality, and according to that Pareto ranking of

all candidate solutions within the population is

commonly used by the selection methods of multi

objective evolutionary algorithms. More than twenty

years ago, Goldberg (1989) outlined the basic idea

which is implemented in the Omni Optimizer, too:

All non

dominated candidate solutions within the

current population are identified, top

ranked and

temporarily suspended. Thereafter, all non

dominated candidate solutions within the remaining

population are identified, next

ranked and

temporarily suspended. This process continues until

the entire population is ranked. Finally, selection

methods can be applied based on that ranking. An-

other population ranking can be defined by counting

how many other individuals each candidate solution

dominates and

or is dominated by within the current

population.

According to Hughes (2005), however,

optimization tools using selection methods based on

Pareto ranking to sort the population will be very

effective only for optimization problems with few

objectives. Coello Coello, Lamont and Van Veld-

huizen (2007) also explain that Pareto ranking

becomes inappropriate when dealing with a large

number of objectives. For such optimization

problems, all the individuals within the population

will soon become non

dominated and selective

pressure decreases. That is why the CHEOPS

selection methods for multi

objective optimization

should not rely on Pareto ranking of all the candidate

solutions with-in the population. Remember that

they have to be implemented both ways, selecting

preferably good candidate solutions to reproduce

and rather bad ones to die.

6.2 Elite Population Archiving

Strategies

In single

objective optimization, elitism was simply

keeping track of the best candidate solution(s) found

so far while the evolutionary algorithm is running.

However, in multi

objective optimization all such

candidate solutions should be kept that are not

dominated by any other(s). That is why a separate

elite population must be reviewed continually and

updated accordingly. Eventually it may contain hun-

dreds even thousands of non

dominated candidate

solutions being as close as possible to the true trade

off surface for the current optimization problem.

Hence, some archiving strategy would make

sense to implement in CHEOPS not keeping all but

only a limited number of such candidate solutions.

Of course, they should cover the trade

off surface as

widespread as possible within the objective space.

This can be achieved by maximizing the inner

distances between the candidate solutions kept in the

elite population, or by maximizing the area

(hyper-

)

volume they dominate. According to Corne and

Knowles (2003), however, this essentially leads to

Free Lunch results for archived multi

objective

optimization.

ICEC 2010 - International Conference on Evolutionary Computation

318

7 SUMMARY

AND CONCLUSIONS

This paper has introduced the Chemnitz Hybrid

Evolutionary Optimization System to the scientific

community. Being a non

standard genetic algorithm

framework, CHEOPS allows simple as well as ad-

vanced modes of operation.

In the present paper we have restricted ourselves

to single

objective optimization, because CHEOPS

is still under construction. It will be enhanced to

solve multi

objective problems as well. Thus, an-

other paper might take up the comparison in the near

future. Surprisingly, steady state genetic algorithms

like CHEOPS are rather unusual in multi

objective

optimization practice

without any justification and

perhaps unaware of their main advantage. The

proposed enhancement to solve multi

objective

problems simply by appropriate selection methods

and elite population archiving strategies is indeed

quite straightforward. Furthermore, CHEOPS does

not need any other modifications such as variable

space and objective space crowding, or niche and

speciation methods.

In their pioneering papers, Deb and Tiwari

(2005, 2008) have argued that multi

objective,

multi

optima optimization problems are the most

generic ones. They have concluded that, if designed

carefully, an algorithm capable of solving such

problems should also solve single

objective and

uni

optimal problems in a straightforward, so

called

“degenerated” manner. However, due to the

disappointment of their (extended) Omni Optimizer

with regard to its single

objective optimization

results as assessed in the present paper, a high

performance genetic algorithm well

suited for solv-

ing both single

and multi

objective optimization

problems is still a matter of serious research. It

might be acknowledged by the scientific community

in the near future and should find increasing use in

real

world optimization practice, too.

Let us finally think about that reasoning of Deb

and Tiwari

in more detail. In multi

objective

optimization, the optimization tool should output

lots of such candidate solutions that cannot be

dominated by any other(s), thus spanning the trade

off surface for the current optimization problem in

the objective space. That is known as Pareto

optimality, but being a pareto

optimal candidate

solution does not require getting close to extreme in

one or more objective function(s). Unlike, getting

close to extreme is what single

objective

optimization is all about! In multi

objective

optimization, there are usually infinitely many

pareto

optimal candidate solutions

in single

objective optimization, the optimization tool has to

push the objective function to its very extreme to

find the true, one and only global optimum. Thus, it

is the author’s opinion, that single

and multi

objective optimization are two different jobs, and

you cannot perform well in one job just by “de-

generation” of the skills you have trained for and

practiced in another job.

REFERENCES

Coelho, Guilherme P.; Von Zuben, Fernando J. (2006).

Omni

aiNet: An Immune

Inspired Approach for

Omni Optimization. In Proceedings of the Fifth

International Conference on Artificial Immune

Systems ICARIS’2006 (pp. 294

308). Berlin:

Springer LNCS 4163.

Coello Coello, Carlos A.; Lamont, Gary B.; Van Veld-

huizen, David A. (2007). Evolutionary Algorithms for

Solving Multi

Objective Problems (Second Edition).

New York: Springer.

Corne, David W.; Knowles, Joshua D. (2003). Some

Multiobjective Optimizers are Better than Others. In

Proceedings of the 2003 IEEE Congress on Evolution-

ary Computation CEC’2003 (pp. 2506

2512). Pis-

cataway: IEEE Service Center.

Deb, Kalyanmoy; Pratap, Amrit; Agarwal, Sameer; Me-

yarivan, Thirunavukkarasu (2000). A Fast and Elitist

Multi

Objective Genetic Algorithm: NSGA

II. Indian

Institute of Technology Kanpur : KanGAL Report No.

200001.

Deb, Kalyanmoy; Pratap, Amrit; Agarwal, Sameer; Me-

yarivan, Thirunavukkarasu (2002). A Fast and Elitist

Multiobjective Genetic Algorithm: NSGA

II. IEEE

Transactions on Evolutionary Computation, 6

(2), pp.

182

197.

Deb, Kalyanmoy; Tiwari, Santosh (2005). Omni

Optimi-

zer: A Procedure for Single and Multi

Objective Opti-

mization. In Proceedings of the Third International

Conference on Evolutionary Multi

Criterion

Optimization EMO’2005 (pp. 47

61). Berlin:

Springer LNCS 3410.

Deb, Kalyanmoy; Tiwari, Santosh (2008). Omni

Optimi-

zer: A Generic Evolutionary Algorithm for Single and

Multi

Objective Optimization. European Journal of

Operational Research, 185

(3), 2008, 1062

1087.

De Jong, Kenneth A. (2006). Evolutionary Computation

A Unified Approach. Cambridge : MIT Press.

Goldberg, David E. (1989). Genetic Algorithms in Search,

Optimization, and Machine Learning. Boston: Addi-

son

Wesley.

Hughes, Evan J. (2005). Evolutionary Many

Objective

Optimisation: Many Once or One Many? In

Proceedings of the 2005 IEEE Congress on

Evolutionary Computation CEC’2005 (pp. 222

227).

Piscataway: IEEE Service Center.

THE CHEMNITZ HYBRID EVOLUTIONARY OPTIMIZATION SYSTEM

319

Klanac, Alan; Jelovica, Jasmin (2007). A Concept of

Omni

Optimization for Ship Structural Design. In

Advancements in Marine Structures

Proceedings of

the First International Conference on Marine Struc-

tures MARSTRUCT’2007 (pp. 473

481). London:

Taylor

Francis.

Nieländer, Ulf (2009). CHEOPS: Das Chemnitzer hybrid

evolutionäre Optimierungssystem. Chemnitz Univer-

sity of Technology: Eng.

D. Thesis. http://archiv.tu-

chemnitz.de/pub/ 2009/0100/data/UlfNielaender.pdf

Schwefel, Hans

P. (1975). Evolutionsstrategie und nume-

rische Optimierung. Technical University of Berlin:

Eng.

D. Thesis.

Schwefel, Hans

P. (1995). Evolution and Optimum

Seeking. New York: Wiley.

Wolpert,

David

H.;

Macready,

William

(1995).

Free

Lunch Theorems for Search. Santa Fe Institute:

Working Paper 95-02-010.

ICEC 2010 - International Conference on Evolutionary Computation

320