FUZZY ANP

A Analytical Network Model for Result Merging for Metasearch using Fuzzy

Linguistic Quantifiers

Arijit De

TCS Innovation Labs-Mumbai, Tata Consultancy Services, Pokhran Road, Thane (W), Mumbai, 400601, India

Elizabeth Diaz

Department of Math and Computer Science, University of Texas- Permian Basin, Texas, U.S.A.

Keywords: Information Retrieval, Fuzzy Sets, Soft Computing, Multi-criteria Decision Making.

Abstract: Search Engines are tools for searching the World Wide Web or any other large data collection. Search

engines typically accept a user query and returns a list of relevant documents. These documents are

generally returned as a result list for the user to see. A metasearch engine is a tool that allows an information

seeker to search information on the world wide web through multiple search engines. A key function of a

metasearch engine is to aggregate search results returned by many search engines. Result aggregation is an

important task for a metasearch engine. In this paper we propose a model for result aggregation for

metasearch, Fuzzy ANP, that employs fuzzy linguistic quantifier guided approach to result merging using

Saty's Analytical Network Process. We compare our model to two existing result merging models, the

Borda Fuse model and the OWA model for metasearch. Our results show that our model outperforms the

OWA model and Borda-Fuse model significantly.

1 INTRODUCTION

A metasearch engine expands the scope of web

search by using multiple search engines to search for

information in parallel in response to a user query.

Search engines return web documents relevant to a

query as a ranked result list of documents. The

metasearch engine then aggregates the ranks

obtained by documents from various search engines

to create a merged list of web documents. The result

aggregation problem for metasearch can be

modelled as multi criteria decision making (MCDM)

problem with search systems being the judges and

documents being the alternatives to be ranked by

them.

In this paper we propose a model for result

merging, Fuzzy ANP, which is based on Saty’s

Analytical Network Process (ANP) (Saty, 1996) and

employs Fuzzy Linguistic Quantifiers proposed by

Zadeh (Zadeh, 1983) and Yager (Yager, 1986) in

conjunction with ANP. We compare the

performance of our model with two well established

models for result merging. The first of these models

is the fuzzy result merging model OWA proposed by

Diaz (Diaz, 2004) based on Yager’s (Yager, 1983)

OWA operator and the second is the Borda-Fuse

model proposed by Aslam and Montage (Aslam and

Montague, 2001) based on Borda Count (Borda

1781). In subsequent sections of this paper we

review existing result merging models and then

discussing the proposed Fuzzy ANP model, our

experiments, and results of them and finally

summarize our discussions in a conclusion.

2 PREVIOUS WORK

The most popular model for result aggregation was

the Borda-Fuse model proposed by Aslam and

Montague (Aslam and Montague, 2001). Diaz (Diaz,

2004) applied Yager’s (Yager, 1983) OWA operator

to create a result aggregation model for metasearch.

The Borda-Fuse model was proposed by Aslam

and Montague (Aslam and Montague, 2001) based

De A. and Diaz E..

FUZZY ANP - A Analytical Network Model for Result Merging for Metasearch using Fuzzy Linguistic Quantiﬁers.

DOI: 10.5220/0003059400730078

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICFC-2010), pages

73-78

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

on the Borda-Count (Borda, 1781). The model

assigns a specific number of “Borda” points, let us

say d, to the top document in each list to be merged.

The next document is assigned d-1 Borda points and

so on. Remaining points are distributed amongst

documents that exist in some result lists but are

missing in others. The documents are ranked in

descending order according to the total number of

points accumulated in these lists.

Diaz (Diaz, 2004) applies the OWA operator for

result aggregation in a metasearch model. The OWA

model uses a measure similar to Borda points, called

positional values. The positional value (PV) of a

document d

in the result list l

returned by a search

engine s

is defined as (n – r

+ 1) where, r

is the

rank of d

in search engine s

and n is the total

number of documents in the result. Thus, the top

ranked document in a result list has the highest

positional value. One shortcoming of the Borda-Fuse

model is that it handles missing documents by

distributing the remaining points available to them

uniformly without considering individual document

popularities. Reasons for missing documents are

obvious as coverage of search systems vary. Diaz

(Diaz, De, and Raghavan, 2005) addresses this issue

by proposing two simple heuristics for handling

missing documents by calculating a virtual

positional value of the document from its positional

value in other lists where it appears

Let us now look at the OWA operator proposed

by Yager (Yager, 1983). The OWA operator was

original proposed by Yager as multi-criteria decision

making (MCDM) approach. Let A

, A

….. A

be n

criteria of concern in a multi-criteria decision

making problem and x be a alternative, being rated

by/against these criteria. A

(x) ε [0, 1] indicates the

degree to which x satisfies the j

criteria. Yager

(Yager, 1983) comes up with a decision function F

to combine these criteria and evaluate the degree to

which the alternative x satisfies the criteria. Let

(x), a

(x), and a

(x).The OWA

decision function is F (a

, a

, ..., a

) = ∑w

·b

for

all j, 1 ≤ j ≤ n. Here b

is the j

greatest a

. Here w

the ordered weight vector attached to the j

criteria

and such that the ordered weight vector W = [w

, w

…..,w

] associated with the OWA operator is key to

determining the “orness” of the aggregation.

In the OWA model for metasearch, Diaz (Diaz,

2004) uses the Yager (Yager, 1986) approach to

computing OWA weights using linguistic

quantifiers. The weight associated with the i

criterion (positional value associated with a search

engine) is given by w

= Q(i/n) – Q((i-1)/n). Here, Q

is a Regular Increasing Monotone quantifier of the

form Q(r) = r

. The orness associated with the

quantifier, orness(Q) = 1/(1+α). In the OWA model,

each search engine is a criteria, each document an

alternative and the positional value of the document

in a search engine result list corresponds to the

extent to which a document (alternative) satisfies a

search engine (criteria) for a specific query.

Documents are ranked in descending order of F

computed by the OWA operator.

The OWA model for metasearch assigns weights

to the positional values of documents based on the

order. While it is comprehensive in handling missing

documents, it does not explore the relationship

between documents and search engines in pair wise

comparisons. Saty (Saty, 2007) highlights the

advantages of pair wise comparisons in MCDM

problems. To create a model that explores the

relationship between documents and search engines,

we came with the Fuzzy ANP model for metasearch.

3 PROPOSED MODEL

Our main motivation was to build a model that

analyzed the close relationship between documents

and search engines in a pair wise comparison. While

Saty’s Analytical Hierarchy Process (AHP) is a

more popular MCDM approach, we chose to build

our model on the more generic Analytical Network

Process (ANP) as the core structure of the

metasearch problem is not hierarchical in nature.

Let us describe the Analytical Network Process,

before proceeding to give an overview of Fuzzy

Linguistic Quantifiers developed by Yager (Yager,

1986) which is used in transforming the ANP super

matrix to a weighted (column stochastic) super

matrix.

3.1 Analytical Network Process

Saty proposed two MCDM techniques, the

Analytical Hierarchy Process (AHP) (Saty, 1980)

and the Analytical Network Process (ANP) (Saty,

1996). While the AHP is considered the technique of

choice for most hierarchical MCDM problems, the

ANP is used when the problem cannot be structured

hierarchically because the problem involves the

interaction and dependence of higher level elements

on a lower level element (Saty, 1996). Moreover,

when the problem is not hierarchical in nature the

Analytical Network Process (ANP) is more

appropriate.

The first step in the ANP process is model

construction and problem structuring. In this step the

ICFC 2010 - International Conference on Fuzzy Computation

key components in the model, alternatives and

criteria need to be clearly identified and their

relationships captured through the creation of a

network. The structure can be obtained by the

opinion of decision makers through brainstorming or

other appropriate methods.

The second step is the creation of pair wise

comparison matrices and priority vectors. In ANP

decision elements at each component are compared

pair wise with respect to their importance towards

their control criterion, and the components

themselves are also compared pair wise with respect

to their contribution to the goal. Pair wise

comparisons where two alternatives or two criteria at

a time can be done quantitatively or by discussing

with experts. In addition, if there are

interdependencies among elements of a component,

pair wise comparisons also need to be created, and

an eigenvector can be obtained for each element to

show the influence of other elements on it. The

relative importance values are determined with

Saaty’s 1-9 scale where a score of 1 represents equal

importance between the two elements and a score of

9 indicates the extreme importance of one element

(row component in the matrix) compared to the

other one (column component in the matrix).

Let us formalize the notion of pair wise

comparisons and construction of the super matrix.

Let us say we have a set of alternatives A =

,……,a

} and a set of criterion C = {c

,……,c

Using the 9 point scale we can compare alternatives

pair wise for each criterion, based on the degree to

which the alternative satisfies the criterion. Thus for

each alternative a

in A we can obtain a pair wise

matrix M. Each element of the matrix M, m

represents a quantified result of pair wise

comparison of alternatives a

and a

. Here 1/9 ≤ m

≤9 as per the 9 point scale. In the 9 point scale, the

values m

is 1,3,5,7 and 9 if a

is equally, weakly,

strongly, very strongly and absolutely more

important than a

respectively. The values m

is 1/3,

1/5, 1/7 and 1/9 if a

is weakly, strongly, very

strongly and absolutely more important than a

. To

obtain the priority vectors we divide each element of

the matrix M by the sum of the column and then

average out the values. Thus we can obtain for each

criteria c

a priority vector V = {V

, where 1 ≤ j ≤ p}

and each V

represents the alternative a

. Thus for

each (c

, a

) we get a value V

Similarly, criteria can also be compared pair

wise with reference to alternatives, depending on

how each pair of criteria (c

, c

) measure up with

respect to an alternative, for all c

, c

in C. Similarly

priority vectors can be created for each alternative a

such that we obtain a priority value V

for (a

, c

The third step in the process is to create a super

matrix. The super matrix concept is similar to the

Markov chain process. To obtain global priorities in

a system with interdependent influences, the local

priority vectors are entered in the appropriate

columns of a matrix. As a result, a super matrix is

actually a partitioned matrix, where each matrix

segment represents a relationship between two nodes

(components or clusters) in a system.

To put it simply the super matrix is a matrix that

contains each priority vector corresponding to

criteria and alternatives. The super matrix is a square

matrix with each alternative and each criteria being a

row element and as well as a column element. Each

priority vector for an alternative and criterion is

placed in the column for that alternative or criterion

in the super matrix.

The super matrix created must be raised to a

higher power till it converges to a limiting super

matrix. Convergence occurs when each column of

the super matrix contain identical values. Thus final

scores are obtained for each alternative from their

corresponding row values in the limiting super

matrix. However for the initial super matrix created

to converge it needs to be column stochastic. This

means that all column values need sum up to 1. Thus

prior to creating a limiting super matrix, each

element in every column of the super matrix needs

to weighted such the sum of elements in the column

need to sum up to unity. This intermediate step

results in the creation of a weighted super matrix.

3.2 Linguistic Quantifiers

Our model for result merging, Fuzzy ANP is based

on the Analytical Network Process of ANP. While

the backbone of the model is the Analytical Network

Process, we use a Fuzzy Linguistic Quantifier

Guided approach to transforming the super matrix

into the column stochastic weighted super-matrix.

Linguistic quantifiers have been used to generate

ordered weights for aggregation in the OWA

operator (Yager, 1986). Zadeh (Zadeh, 1983)

introduced linguistic quantifiers as way to

mathematically model linguistic terms such as at

most, many, at least half, some and few and

suggested a formal representation of these linguistic

quantifiers using fuzzy sets. In classical logic, only

two fundamental quantifiers are used. These

quantifiers are “there exists” a certain number and

“all”. Zadeh breaks up quantifiers into two types:

absolute and relative. Absolute quantifiers can be

represented as zero or positive real numbers, such as

FUZZY ANP - A Analytical Network Model for Result Merging for Metasearch using Fuzzy Linguistic Quantifiers

“about 5,” “greater than 10.” Relative quantifiers are

terms such as “most,” “few,” or “about half.” Yager

(Yager, 1986) distinguished three categories of these

relative quantifiers. Of these the most popular

quantifier is the Regular Increasing Monotone

(RIM) quantifier of the form Q(r) = r

, mentioned

earlier. Yager (Yager, 1986) shows how to model

these quantifiers, to obtain weights for his OWA

operator as described earlier. When

criteria/alternative importances are available Yager

uses equation 1 to compute weights.

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

∑∑

−

Q(x)w

(1)

Here u

is the weights of the k

criteria to be

merged. One property of the weights so generated is

that they always add up to unity. We exploit this

feature in the construction of the weighted super

matrix.

In our Fuzzy ANP model for metasearch we

borrow this notion of linguistic quantifier guided

weights in transforming the constructed super matrix

to the weighted (column stochastic) super matrix.

Let us illustrate the working with the help of an

example. Let us say that a column of our super

matrix constructed is of the form [0, 0, 0, 0.8, 0.6,

0.4]

. Clearly these values do not add up to unity

and therefore the column is not stochastic. To

transform this column into a column stochastic

matrix we compute Fuzzy Linguistic Weights using

the equation 3. Here u

, u

and u

are 0 while u

0.8, u

= 0.6 and u

= 0.4. Let us say we apply a

weight of α = 1 (for simplicity). Weights w

, w

and

are 0. Weight w

= 0.44, w

= 0.337 and w

0.222. Now our column becomes [0, 0, 0, 0.44,

0.337, 0.222].

3.3 Proposed Model

Our proposed model Fuzzy ANP is based on Saty’s

(Saty, 1996) Analytical Network Process (ANP). In

our model in order to apply the Analytical Network

Process, we treat our search engines (criteria) and

documents (alternative) as nodes in a network. The

steps are outlined below.

Step 1 Modelling document and Search Engines

relationships in a network. Each document and

search engine appear as nodes in the network. If a

document is retrieved and ranked/scored by a search

engine then we model it by creating an edge between

the search engine and the document. If a document

does not appear in the result list of a search engine

then there is no edge created between the document

and the search engine. In all subsequent pair wise

comparison, involving the document and the search

engine the appropriate element in the matrix is

assigned a value of 0. Thus missing documents are

factored in without the employment of heuristics.

Step 2 Pair Wise Comparison of Documents and

Search Engines. With this creation of a network of

nodes, we can proceed to do pair wise comparison of

documents based on their ranks/scores obtained

from different search engines. Let us say we have

two documents D

and D

. A search engine SE

returns a relevance score of SC

and SC

for them

respectively. The pair-wise comparison value

P(SE

, D

) = ((SC

- SC

)/( SC

MAX

- SC

MIN

))*9. If

only ranks are available, then we replace ranks R

and R

are used for documents D

and D

respectively. Here SC

MAX

and SC

MIN

are the

maximum scores obtained by any document in the

list. These pair wise comparison values are stored in

a matrix, which can be normalized by dividing each

column by a sum of all elements in the column and

then by taking the average of each row. Similarly

search engines can be compared pair-wise based on

ranks/scores they give documents. Using the results

of pair-wise comparison we can construct pair-wise

comparison matrices and compute priority vectors

for documents specific to the search engine and

search engines specific to a document. The priority

vector specific to document D

would be Vector

SE1

,…,S

SEn

]. Here we assume n search engines.

Similarly a vector can be created for every search

engine whose results are being merged.

Step 3 Constructing the Super Matrix. Next we

create super matrix that holds all search engine and

document priority vectors as columns. The super

matrix is created with each search engine and

document being a row as well as a column element.

Each document priority vector is placed in a column

for the corresponding document with values in the

priority vector representing each search engine

going into the row for each search engine. Similarly

search engine priority vectors can be places in

columns for their specific search engines.

Step 4 Transforming the Super Matrix to form a

Weighted Super Matrix. For the ANP to converge

we need to transform the super matrix to a column

stochastic super matrix. This is done by applying

weights to elements in each column such that all

column values add up to unity. We take the column

values and use them as inputs in computing

linguistic fuzzy weights as developed by Yager

(Yager, 1986) and described in equation 3 and the

subsequent example (section 3.2). This makes the

ICFC 2010 - International Conference on Fuzzy Computation

matrix column stochastic as the linguistic fuzzy

weights add up to unity.

Step 5 Computing Limiting Super Matrix. This is

done raising the weighted super matrix to a higher

power to achieve column convergence. The rows

corresponding to the documents contain the final

scores for the documents. The documents can be

sorted by scores obtained in the merged result list.

4 EXPERIMENTS AND RESULTS

The focus of our experiments is to study the

performance of our Fuzzy ANP model for result

merging and compare it with the performance of the

Borda-Fuse and OWA models. We do this

performance comparison for score-based result

merging when document scores from search engines

are available.

We use the OHSUMED collection compiled by

Hersh (Hersh, Buckley, Leone, and Hickam, 1994)

constituted in LETOR 2 (Learning TO Rank) (Liu,

Xu, Qin, Xiong, and Li, 2007) dataset. The

collection consists of 106 queries. The degree of

relevance for each query-document pair is pre-

judged and categorized as 0 (non relevant), 1

(possibly relevant) and 2(definitely relevant). There

are a total of 16,140 query-document pairs with

relevance judgments. There are 25 features for each

document and relevance scores between 0 and 1,

based on these features are provided for each query.

For our experiments features are treated as search

systems and the result list of documents returned by

them along with document scores for the 106 queries

in the OHSUMED dataset are treated as result lists

for merging.

The objective of our experiments is to gauge the

performance of our model in terms of RB precision

of the aggregated result list and compare it with the

performance of the Borda-Fuse and OWA models.

In our experiments we vary the number of result lists

being merged from 2 and 12. Search systems and

queries are picked at random. We merge these result

lists using the OWA, Borda-fuse and Fuzzy ANP

models. For our Fuzzy ANP model and the OWA

model, we vary the Linguistic Quantifier parameter

α, from 0.25 to 2, that is used to compute ordered

weights in the OWA model and column stochastic

weights in our Fuzzy ANP model. We calculate the

RB-precision of the merged list from each of the

models based on relevance judgements provided as

part of the dataset for standard recall levels of 0.25,

0.5, 0.75 and 1 and compute the average. Over 1000

iterations of experiments are performed.

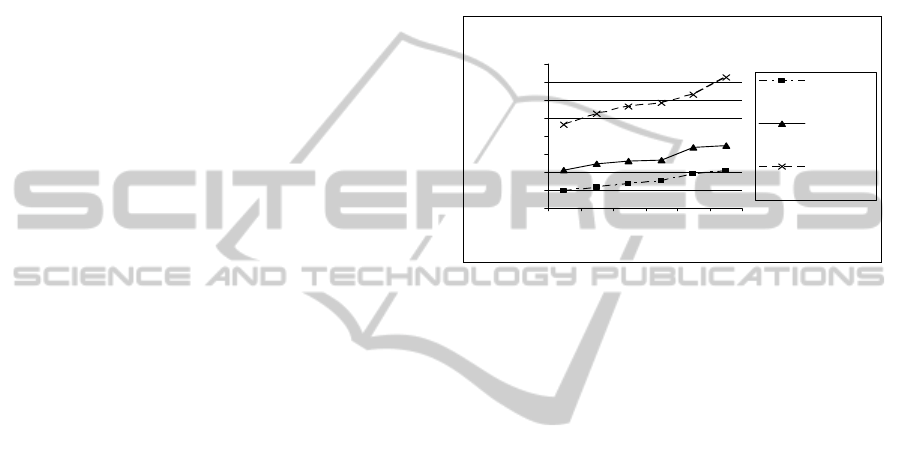
Figure 1 shows the variation is average precision

when the number of search engines being varied (N).

The benefits of metasearch are illustrated by the

results as the overall average precision of the

merged result list goes up when merging more

number of search engines. Clearly the OWA model

outperforms the Borda-Fuse. Also, our Fuzzy ANP

model outperforms the Borda-Fuse model and the

OWA model as demonstrated by Table 1.

Model pe rfor m ance: Average Precis ion vs. N

0.3000

0.3500

0.4000

0.4500

0.5000

0.5500

0.6000

0.6500

0.7000

246810

Average Precision

Average

Precis ion

Borda-Fuse

Average

Precis ion

OWA

Average

Precis ion

Fuzzy ANP

Figure 1: Model Performance over variation of N

Figure 2 shows the variation is average precision

when the Linguistic Quantifier parameter α used to

compute weights is varied from 0.25 through to 2.

Consistent with the findings of Diaz (Diaz, 2004),

the performance of the OWA model is best when α =

0.25 and goes down to a lowest value when α = 1.

When α increases beyond that value the performance

in terms of RB-precision goes up. However, this is

not the case for our Fuzzy ANP model. The

performance of the OWA model is poorest when

‘orness’ of aggregation is balances i.e., under simple

averaging conditions. Under conditions of high

orness when α ≤ 1 and under high andness

conditions when α ≥ 1 the model performance of the

OWA model is higher. However, the performance of

the Fuzzy ANP model gradually goes up when

orness aggregation goes down i.e., as α progresses

from 0.25 towards 2. The Fuzzy ANP model

improves significantly in terms of average Recall

Based (RB) precision by over the OWA and Borda-

Fuse models. Table 2 shows the percentage

improvements of the Fuzz ANP model over the

OWA and the Borda-Fuse models when Linguistic

Quantifier parameter α is varied from 0.25 to 2.5.

5 CONCLUSIONS

In this paper we have proposed a model for result

merging for metasearch that is based on the

FUZZY ANP - A Analytical Network Model for Result Merging for Metasearch using Fuzzy Linguistic Quantifiers

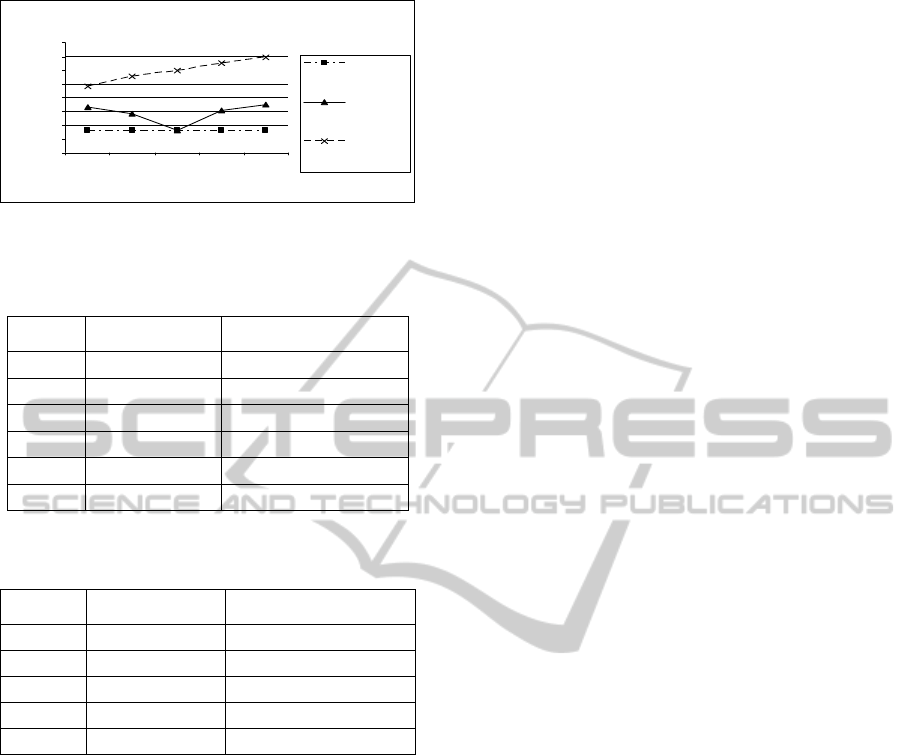
Model Perform ance: Average Precision for ALPHA

0.3

0.35

0.4

0.45

0.5

0.55

0.6

0.65

0.7

0.25 0.5 1 2 2.5

ALPHA

Average Precision

Average

Precision

Borda-Fuse

Average

Precision

OWA

Average

Precision

Fuzzy ANP

Figure 2: Model Performance over variation of α.

Table 1: % Improvement of Fuzzy ANP over OWA and

Borda Fuse when N is varied.

Over OWA Over Borda-Fuse

2 23.7387 97.7623

4 24.6219 97.7170

6 26.2190 97.7787

8 26.7376 97.7885

10 23.7000 97.4114

12 28.4656 97.6761

Table 2: % Improvement of Fuzzy ANP over OWA and

Borda Fuse when α is varied.

α Over OWA Over Borda-Fuse

0.25 14.1722 96.1813

0.5 23.4784 97.5437

1 36.1246 98.3471

2 27.5829 97.7366

2.5 26.8654 97.5906

Analytical Network Process that employs Fuzzy

Linguistic Quantifiers to construct a column

stochastic weighted super matrix for the

convergence of the ANP process. We compare our

model to two existing models for the result

aggregation. The first of these is the non fuzzy result

merging model called Borda Fuse. The second

model is the OWA model based on the Ordered

Weighted Average operator. In our experiments we

try to maximize the average precision of the merged

list coming out of these merging models. Using this

metric we demonstrate that our model improves

upon the OWA model for metasearch by 25% on the

average and by 97% over the Borda-Fuse model.

REFERENCES

Aslam, J., and Montague, M., 2001. Models for

metasearch. In Proceedings of the 24th annual

international ACM SIGIR Conference on Research

and Development in Information Retrieval, New

Orleans, LA, USA. ACM.

Bollmann, P., Raghavan, V. V., Jung, G. S., Shu, L. C.,

1992. On probabilistic notions of precision as a

function of recall. Information Processing and

Management.

Borda, J. C., 1781. Memoire sur les elections au scrutiny,

Paris: Histoire de l’Academie Royale des Sciences.

Diaz, E. D., De, A., Raghavan, V.V., 2005. A

comprehensive OWA-based framework for result

merging in metasearch. In Rough Sets, Fuzzy Sets,

Data Mining, and Granular-Soft Computing, Regina,

SK, Canada. Springer.

Diaz, E. D., 2004. Selective Merging of Retrieval Results

for Metasearch Environments, University of Louisiana

Press, Lafayette, LA.

Hersh, W., Buckley, C., Leone, T. J., and Hickam, D.,

1994. OHSUMED: An interactive retrieval evaluation

and new large test collection for research",

Proceedings of the 17th annual international ACM

SIGIR Conference on Research and Development in

Information Retrieval. ACM/Springer.

Liu, T., Xu, J., Qin, T., Xiong, W., Li, H., 2007. LETOR:

Benchmark dataset for re-search on learning to rank

for information retrieval, LR4IR 2007, in conjunction

with SIGIR 2007. ACM/Springer.

Saaty, T. L., 1980. The Analytic Hierarchy Process,

McGraw-Hill, New York.

Saaty, T.L., 2007. Relative Measurement and its

Generalization in Decision Making: Why Pair wise

Comparisons are Central in Mathematics for the

Measurement of Intangible Factors - The Analytic

Hierarchy/Network Process. Review of the Royal

Spanish Academy of Sciences, Series A, Mathematics.

Saaty, T.L., 1996. Decision Making with Dependence and

Feedback: The Analytic Network Process. RWS

Publications, Pittsburgh.

Yager, R. R., 1983. On ordered weighted averaging

aggregation operators in multi-criteria decision

making, Fuzzy Sets and Systems.

Yager, R. R., 1986.Quantifier guided Aggregating using

OWA operators, International Journal of Intelligent

Systems.

Zadeh, L. A., 1983. A computational approach to fuzzy

quantifiers in natural languages, Computational

Mathematics Application.

ICFC 2010 - International Conference on Fuzzy Computation