CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM

FOR THE SINGLE MACHINE SCHEDULING PROBLEM

WITH SEQUENCE-DEPENDENT SETUP TIMES

Aymen Sioud, Marc Gravel and Caroline Gagn

epartement d’Informatique et Math

ematique, Universit

e du Qu

ebec

a Chicoutimi

555 Boulevard Universit

e, Chicoutimi, Canada

Keywords:

Hybrid crossover, Constrained based scheduling, Total tardiness, Single machine.

Abstract:

This paper presents a hybrid approach based on the integration between Genetic Algorithm (GA) and Con-

straint Based Scheduling (CBS) approaches for solving a scheduling problem. The main contributions are the

integration of the CBS approach in the reproduction and the intensiﬁcation processes of a GA autonomously.

The proposed methodology is applied to a single machine scheduling problem with sequence-dependent setup

times for the objective of minimizing the total tardiness. A sensitivity analysis of the hybrid methodology

is carried out to compare the performance of the GA and the integrated GA-CBS approaches on different

benchmarks from the literature.

1 INTRODUCTION

Several researches on scheduling problems have been

done under the assumption that setup times are inde-

pendent of job sequence. However, in certain con-

texts, such as the pharmaceutical industry, metallur-

gical production, electronics and automotive manu-

facturing, there are frequently setup times on equip-

ment between two different activities. Production of

good schedules often relies on management of these

setup times (Allahverdi et al., 2008). This present

paper considers the single machine scheduling prob-

lem with sequence dependent setup times with the ob-

jective to minimize total tardiness of the jobs (SMS-

DST). This problem, noted as 1|s

i j

|ΣT

in accordance

with the notation of Graham, Lawler, Linstra and Ri-

nooy Kan (1979) , is an NP-hard problem (Du and

Leung, 1990).

The 1|s

i j

|ΣT

may be deﬁned as a set of n jobs

available for processing at time zero on a continu-

ously available machine. Each job j has a processing

time p

, a due date d

, and a setup time s

i j

which is

incurred when job j immediately follows job i. It is

assumed that all the processing times, due dates and

setup times are non-negative integers. A sequence of

the jobs S = [q

, q

,..., q

n−1

, q

] is considered where

is the subscript of the j

job in the sequence. The

due date and the processing time of the j

job in se-

quence are denoted as d

and p

, respectively. Thus,

the completion time of the j

job in sequence will be

expressed as C

∑

k=1

k−1

+ p

) while the tar-

diness of the j

job in sequence will be expressed as

= max(0, C

−d

). The objective of the schedul-

ing problem studied is to minimize the total tardiness

of all the jobs which will be expressed as

∑

j=1

In this paper, we present a hybrid approach based

on Genetic Algorithm (GA) and Constraint Based

Scheduling (CBS) to solve this problem. The CBS

approach has become a widely used form for model-

ing and solving scheduling problems using the con-

straint programming approach. The hybridization of

the CBS approach with the GA is done at two levels.

Indeed, the CBS is used in the reproduction and inten-

siﬁcation processes of GA separately and this repre-

sents the paper’s main contributions. In fact, the CBS

approach is integrated in a crossover operator and in

the intensiﬁcation search space process using addi-

tional constraints for both of them. Computational

testing is performed on a set of test problems avail-

able from literature. We report on our experimental

results and conclude with some remarks and future

research directions. As a constraint programming en-

vironment, we use the ILOG IBM CP environment

using ILOG Solver and ILOG Scheduler via the C++

APIs (ILOG, 2003b; ILOG, 2003a). The use of this

kind of platforms has been encouraged by the steady

137

Sioud A., Gravel M. and Gagné C..

CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING PROBLEM WITH SEQUENCE-

DEPENDENT SETUP TIMES.

DOI: 10.5220/0003060601370145

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 137-145

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

improvement of general purpose solvers over the past

decade. Such solvers have become signiﬁcantly more

effective and robust (Yunes et al., 2010). Also, the

C++ APIs allow users to develop their own strategies

for a particular problem. Moreover, this interface en-

ables a better interaction with other applications than

the OPL interface (ILOG, 2003b).

2 LITERATURE REVIEW

Considering the objective of minimizing the

makespan in the basic single machine problem

without setup times, any permutation of jobs gives

the same makespan. Nevertheless, the addition of

the sequence dependent setup times considerably

complicates the problem (Allahverdi et al., 2008).

This problem with the objective of minimizing the

makespan is equivalent to the Travelling Salesman

Problem (TSP), which is NP-hard. In addition, this

problem is even more difﬁcult when total tardiness

is the performance measure and there has been

relatively little research reported on it. Furthermore,

in presence of sequence dependent setup times, most

of the research has focused on either minimizing the

sum of setup times or minimizing the sum of job

completion times (Allahverdi et al., 2008).

Different approaches have been proposed by a

number of researchers to solve the problem. Rubin

and Ragatz (1995) proposed a Branch and Bound ap-

proach, which quickly showed its limitations. It could

solve to the optimality only small instances of bench-

mark ﬁles of 15, 25, 35 and 45 jobs proposed by these

authors. Bigras, Gamache and Savard (2008) solved

to the optimum all instances proposed by Rubin and

Ragatz (1995) using a Branch and Bound approach

with linear programming relaxation bounds. They

also demonstrated and used the problem’s similarity

with the time-dependent traveling salesman problem.

Such Branch and Bound approach solved some of

these instances by more than 7 days. Because this

problem is NP-hard, many researchers used a wide

variety of metaheuristics to solve this problem such

as genetic algorithm (Franca et al., 2001; Sioud et al.,

2009), memetic algorithm (Armentano and Mazzini,

2000; Franca et al., 2001; Rubin and Ragatz, 1995),

simulated annealing (Tan and Narasimhan, 1997),

GRASP (Gupta and Smith, 2006), ant colonies op-

timization (Gagn

e et al., 2002; Liao and Juan, 2007)

and Tabu/VNS (Gagn

e et al., 2005). Heuristics such

as Random Start Pairwise Interchange (RSPI) (Rubin

and Ragatz, 1995) and Apparent Tardiness Cost with

Setups (ATCS) (Lee et al., 1997) have also been pro-

posed for solving this problem. For their part, Spina,

Galantucci and Dassisti (2003) introduce a hybrid ap-

proach using constraint programming and genetic al-

gorithm sequentially. In this latter case, the authors

have considered a real world problem with a maxi-

mum of ten jobs.

3 THE HYBRID GENETIC

ALGORITHM

In their respective works, Rubin and Ragatz (1995)

and Sioud, Gravel and Gagn

e (2009) have shown the

importance of relative and absolute order positions for

the 1|s

i j

|ΣT

problem. Thereby, all the used crossover

operators into the genetic algorithms from literature

maintain the absolute position, or the relative posi-

tion or both. Indeed, Rubin and Ragatz (1995) used

a speciﬁc operator which alters the conservation of

the absolute and the relative order by generating ran-

dom sub-sequences of jobs separately for each off-

spring. Armentano and Mazzini (2000) modiﬁed the

ERX crossover while Franca, Mendes and Moscato

(2001) developed a genetic and a memetic algorithms

using the OX crossover. Sioud et al. (2009) proposed

RMPX, a new crossover operator which takes greater

account of the relative and absolute position job and

gives better results than other crossovers.

To reach good results, the presented hybrid ge-

netic algorithm must ensure the preservation of both

the relative and the absolute order positions while

maintaining diversiﬁcation during its evolving. In this

context, the genetic algorithm and the two hybridiza-

tion approaches will take this into consideration.

3.1 Genetic Algorithm

Genetic algorithms are methods based upon bio-

logical mechanisms such as the genetic inheritance

laws of Mendel and the natural selection concept of

Charles Darwin, where the best adapted species sur-

vive. The basic concepts of GA have been described

by the investigation carried out by Holland (1992)

who explained how to add intelligence into a program

computing with the crossover exchange of genetic

material and transfer as a source of genetic diversity.

In a GA, a population of individuals or chromosomes

incurs a sequence of transformations by means of ge-

netic operators to form a new population. Two main

operators are used for this purpose : crossover and

mutation. Crossover creates new individuals by com-

bining parts of two individuals and mutation creates

new individuals by a small change in a single individ-

ual.

Based on the GA proposed by Sioud et al. (2009),

ICEC 2010 - International Conference on Evolutionary Computation

138

we redeﬁne a simple genetic algorithm. A solution

is coded as a permutation of the considered jobs. The

population size is set to n to ﬁt with the considered in-

stance size. The initial population is randomly gener-

ated for 60% and also for 20% using a pseudo-random

heuristic which favors setup times and promotes a rel-

ative order for the jobs. The last 20% is generated

using a pseudo-random heuristic which depends on

due dates and promotes an absolute order for the jobs.

A binary tournament selects the chromosomes for the

crossover. The proposed GA uses the OX crossover

(Michalewicz, 1996) to generate 30% of offspring and

the RMPX crossover (Sioud et al., 2009) to generate

the rest of the children population. Both of the OX

and RMPX crossover maintain both of the relative and

the absolute order positions, but the RMPX crossover

seems to give better results. The RMPX crossover can

be described in the following steps : (i) two parents

P1 and P2 are considered and two distinct crossover

points C1 and C2 are selected randomly, as shown in

Figure 1; (ii) an insertion point p

is then randomly

chosen in the offspring E as p

= random (n – ( C2 –

C1)); (iii) the part [C1, C2] of P1, shaded in Figure 1,

is inserted in the offspring E from p

. The insertion is

to be done from the position 2 showing in Figure 1;

and (iv) the rest of the offspring E is completed from

P2 in order of appearance since its ﬁrst position.

3 7658241P1

8 2461375

7 6135824E

Figure 1: Illustration of RMPX.

The crossover probability pc is set to 0.8, i.e.

therefore n*0.8 offspring are generated at each gener-

ation in which a mutation is applied with a probability

pm equal to 0.3. The mutation consists of exchanging

the position of two distinct jobs which are randomly

chosen. The replacement is elitist and the duplicates

individuals in the population were replaced by chro-

mosomes which are generated by one of the pseudo-

random heuristics used in the initialization phase. The

stop criterion is set to 3000 generations.

3.2 Constraint based Scheduling

Constraint solving methods such as domain reduc-

tion and constraint propagation have proved to be

well suited for a wide range of industrial applications

(Fromherz, 1999). These methods are increasingly

combined with classical solving techniques from op-

erations research, such as linear, integer, and mixed

integer programming (Talbi, 2002), to yield power-

ful tools for constraint-based scheduling by adopting

them. The most signiﬁcant advantage of using such

CBS is to separate the model from the algorithms

which solve the scheduling problem. This makes it

possible to change the model without changing the

algorithm used and vice versa.

In the recent years, the CBS has become a widely

used form for modeling and solving scheduling prob-

lems using the constraint programming approach

(Baptiste et al., 2001; Allahverdi et al., 2008). A

scheduling problem is the process of allocating tasks

to resources over time with the goal of optimizing

one or more objectives (Pinedo, 2002). A scheduling

problem can be efﬁciently encoded like a constraint

satisfaction problem (CSP).

The activities, the resources and the constraints,

which can be temporal or resource related, are the

basis for modeling a scheduling problem in a CBS

problem. Based on representations and techniques

of constraint programming, various types of variables

and constraints have been developed speciﬁcally for

scheduling problems. Indeed, the domain variables

may include intervals domains where each value rep-

resents an interval (processing or early start time for

example) and variable resources for many classes of

resources. Similarly, various research techniques and

constraints propagation have been adapted for this

kind of problem.

In Constraint Based Scheduling, the single ma-

chine problem with setup dependent times can be efﬁ-

ciently encoded in terms of variables and constraints

in the following way. Let M be the single resource.

We associate an activity A

for each job j. For each

activity A

four variables are introduced, start(A

end(A

), proc(A

) and dep(A

). They represent the

start time, the end time, the processing time and the

departure time of the activity A

, respectively. The

departure time represents the needed setup time of an

activity when the latter starts the schedule.

A setup time s

i j

is introduced and it is incurred

when job j immediately follows job i. In our case,

the setup times are activity related and not resource-

related. For this purpose, we assign a type to each ac-

tivity and a lattice to the unary machine. Then, when

we calculate the objective function, it is possible to

CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING

PROBLEM WITH SEQUENCE-DEPENDENT SETUP TIMES

139

Figure 2: C++ API model for the 1|s

i j

|ΣT

problem.

associate the transition times between two distinct

types of activities. The tardiness criterion is repre-

sented by an additional variable Tard. Its value is de-

termined by Tard =

∑

max(end(A

) − d

, 0).

Figure 2 presents the pseudo-code for the 1|s

i j

|ΣT

problem modeling with the C++ API of ILOG Sched-

uler 6.0. The main procedure ModelSMSDST calls

the two procedures CreateMachine and CreateJob.

CreateMachine procedure (lines 3 to 6) uses the class

IloUnaryResource. This allows handling unary re-

sources, that is to say, a resource whose capacity is

equal to one. This resource cannot therefore handle

more than one job at a time. The use of the setup times

in CBS and also with ILOG Scheduler 6.0 (ILOG,

2003a) indicates that they are resource-related and not

activity-related such as is the case in our problem. It

is possible to overcome this problem by associating a

type for each activity and creating setup times asso-

ciated with these types. For this purpose, we use the

class IloTransitionParam which is managing and set-

ting setup times. The setup matrix is then associated

to this class which will be related to the unary ma-

chine (line 5). Thus, when we calculate the objective

function, it is possible to associate the setup times be-

tween two distinct types of activities. To model the

total tardiness, we must ﬁrst deﬁne a variable Tard

(line 16). Then we deﬁne an array C containing the

completion times C

of the different activities times A

during the research phase (line 15). When we create

the activities in the model, we add a constraint that

combines the activities A

to the corresponding times

(line 19). After that, we add a constraint which

combines the variable Tard with the sum of the C

the table C (line 21). Finally, we add a constraint that

minimizes the variable Tard (line 22). Thus, we ob-

tain the objective function which will be added to the

model.

ILOG Solver (2003) provides several predeﬁned

search algorithms named as goals and activity se-

lectors. We used the IloSetTimesForward algorithm

with the IloSelFirstActMinEndMin activity selector.

The IloSetTimesForward algorithm schedules activi-

ties on a single machine forward initializing the start

time of the unscheduled activities. The activity se-

lector deﬁnes the heuristic scheduling variables rep-

resenting start times, which chooses the next activ-

ity to schedule. The IloSelFirstActMinEndMin tries

ﬁrst the activity with the smallest start time and in

case of equality the activity with the smallest end

time. For his part, ILOG Scheduler (2003) provides

four strategies to explore the search tree : the default

Depth-First Search (DFS), the Slice-Based Search

(SBS) (Beck and Perron, 2000), Interleaved Depth-

First Search (IDFS) (Meseguer, 1997) and the Depth-

Bounded Discrepancy Search (DDS) (Walsh, 1997)

which is used in this work.

ICEC 2010 - International Conference on Evolutionary Computation

140

3.3 Hybrid Approach

The hybridization of an exact method such as the

CBS and a metaheuristic such as the GA can be car-

ried out in several ways. Talbi (2002) presents a

taxonomy dealing with the hybrid metaheuristics in

general. Puchinger and Raidl (2005) and Jourdan,

Basseur and Talbi (2009) present a taxonomy for the

exact methods and metaheuristics hybridizing. In

this paper we present two different approaches of hy-

bridization. The ﬁrst approach is to integrate the CBS

in the GA reproduction phase and more precisely in

a crossover operator, while the second approach is to

use CBS as an intensiﬁcation process in the GA.

When we handle a basic single machine model,

there is no precedence constraint between activities

as is the case in a ﬂow-shop or job-shop where adding

constraints improves the CBS approach. The main

idea of integrating the CBS in a crossover is to provide

to this latter precedence constraints between activi-

ties when generating offspring. In this work, we con-

sider only the direct constraints during the crossover.

Therefore, the conceived crossover promotes the rel-

ative order positions such as the PPX crossover (Bier-

wirth et al., 1996). The proposed crossover operator is

designated Precedence Constraint Crossover (PCX)

and can be described in the two following steps : (i)

two parents P1 and P2 are considered and the prece-

dence constraints between activities concurrently in

both parents are kept, as shown in Figure 3; and (ii)

the CBS approach tries to solve the problem while

adding the precedence constraints built in the previous

step and an upper bound consisting of the objective

function value of the best parent. The upper bound is

added to discard faster bad solutions when branching

during the solver process. As a reminder, the ILOG

Solver uses a Branch and Bound approach to solve

a problem (ILOG, 2003b). In the case of Figure 3,

the two precedence constraints (4 before 6) and (7 be-

fore 5) are added to the model and will be propagated.

Thus, these two constraints, preserve the relative po-

sitions of the pairs of activities (4,6) and (7,5). E1, E2

and E3 represent three potential offspring where the

two precedence constraints (4 before 6) and (7 before

5) are preserved. Then, if the two selected parents are

”good” solutions, preserving the relative order could

in turn generate also ”good” solutions. Finally, if no

solution is found by the PCX crossover, the offspring

is generated by one of the pseudo-random heuristics

used in the initialization phase. The PCX crossover

will be done under probability p

PCX

Integrating an intensiﬁcation process in a genetic

algorithm has been applied successfully in several

ﬁelds. The incorporation of heuristics and/or other

methods, i.e. an exact method such as the CBS ap-

proach, into a genetic algorithm can be done in the

initialization process to generate well-adapted initial

population and/or in the reproduction process to im-

prove the offspring quality ﬁtness. Following this lat-

ter reasoning, the strategy proposed in this paper is

based on the intensiﬁcation in speciﬁc space search

areas. However, we can ﬁnd in literature only few pa-

pers dealing with such hybridization (Puchinger and

Raidl, 2005; Talbi, 2009).

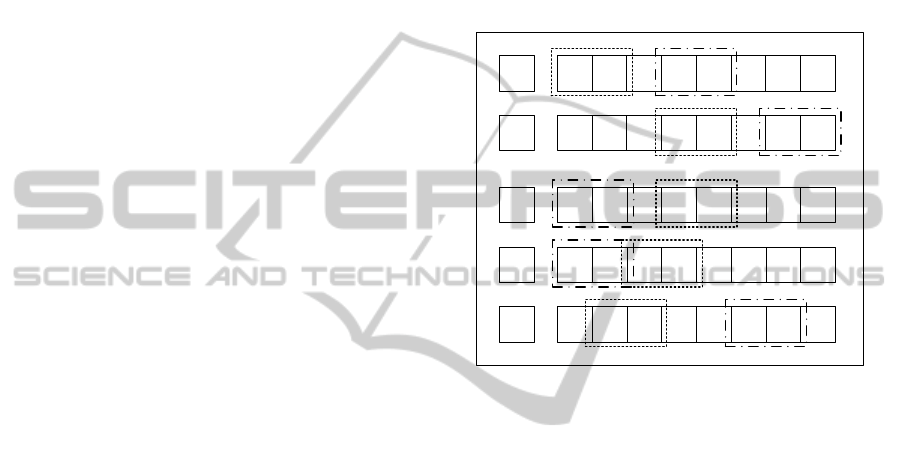
4 1285736P1

2 5716483P2

7 3126485E1

7 2381645E2

8 1572364E3

Figure 3: Illustration of PCX.

In the same vein of the PCX conservation prece-

dence constraints, an intensiﬁcation process is applied

by giving a generated offspring to the CBS approach

and ﬁxing a block of α positions. Thus, the abso-

lute order position will be preserved for these ﬁxed

positions while the relative order position will be pre-

served for the other activities. Indeed, the activities

on the left of the ﬁxed block will be scheduled before

this late block, while the activities on the right will

be scheduled after this block. The ﬁxed block size

should be neither too large nor too small : if its size is

too large, the CBS approach will have no effect and if

its size is too small the CBS approach will consume

more time to ﬁnd a better solution. Thereby, at each

time this intensiﬁcation is done, α continuous posi-

tions are ﬁxed with 0.2*n ≺ α ≺ 0.4*n. We use to

this end two different procedures based on the CBS

approach. The ﬁrst one, noted as IP

TARD

, selects a

generated offspring and tries to solve the problem us-

ing the CBS approach which minimizes the total tar-

diness described above while adding an upper bound

consisting of the objective function value of this off-

spring. So as a result, the CBS approach may return a

better solution when scheduling separately the activi-

ties on the left and the right of the ﬁxed block activi-

ties.

CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING

PROBLEM WITH SEQUENCE-DEPENDENT SETUP TIMES

141

Using the similarity of the studied problem with

the time-dependent traveling salesman problem (Bi-

gras et al., 2008), the second intensiﬁcation proce-

dure, noted as IP

T SP

, works like IP

TARD

but in this

case the CBS approach minimizes the makespan. The

makespan optimization aims to minimize the setup

times and then, in some speciﬁc conﬁgurations, will

give promising solutions under total tardiness opti-

mization otherwise explore a different areas search

space. The makespan criterion is represented by an

additional variable Makespan. Its value is determined

by Makespan =

∑

max(end(A

)). The model

minimizing the makespan is similar to that in Fig-

ure 2. Indeed, we just delete the declaration of the

array C at line 15 and deﬁne an activity Makespan

with time processing equal to 0 at line 16. Then, a

constraint stating that all jobs must be completed be-

fore the Maskespan start time is added in the for loop.

Finally, lines 19 and 21 are removed and line 22 min-

imizes in this case the Makespan end time.

Thereby, an offspring is selected with a tourna-

ment under probability p

and then, one of the two

intensiﬁcation procedures IP

TARD

and IP

T SP

is chosen

under probability p

cip

to be applied on this offspring.

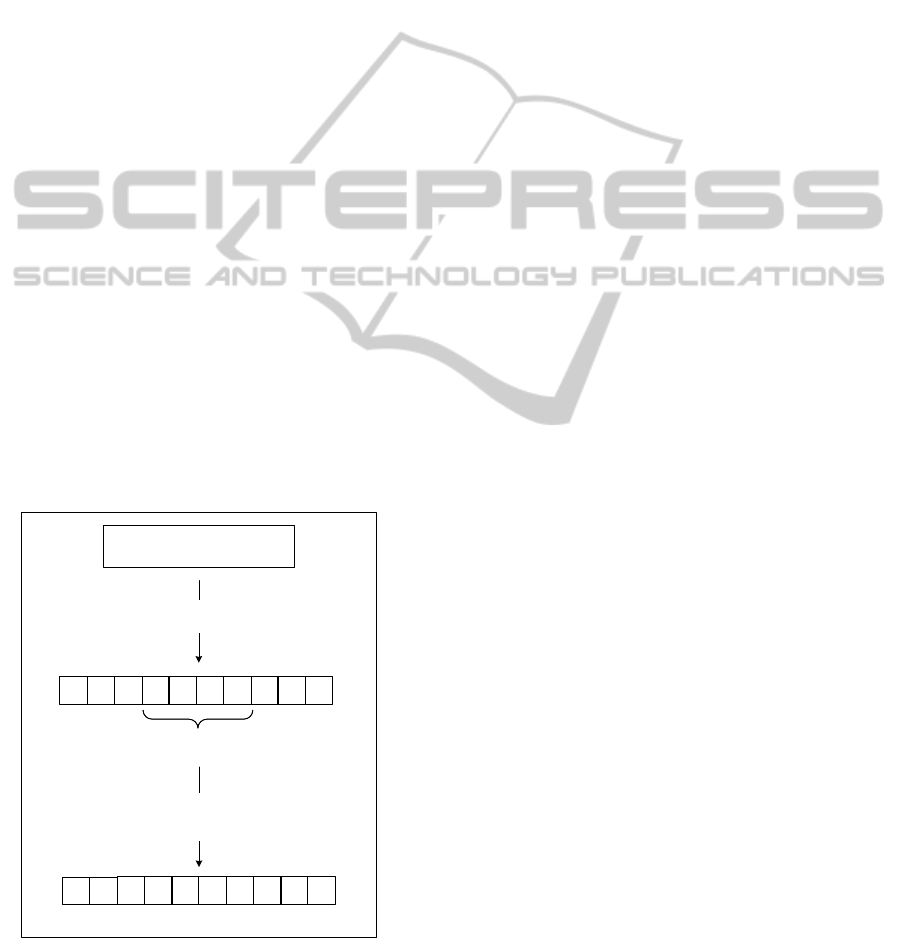
Figure 4 illustrates the intensiﬁcation process based

on the CBS approach. At each generation, an off-

spring is selected under probability p

with tourna-

ment selection. After ﬁxing α positions and choosing

an intensiﬁcation procedure, IP

TARD

or IP

T SP

under

probability p

cip

, the solver tries to ﬁnd a solution. If

no solution is found the offspring is unchanged.

Population (t)

α fixed positions

Tournament selection

under probability p

Final offspring

Choose and apply an intensification

procedure under probability p

cip

Figure 4: The intensiﬁcation process.

4 COMPUTATIONAL RESULTS

AND DISCUSSION

The benchmark problem set consists of eight in-

stances, each with a number of jobs of 15, 25, 35

and 45 jobs, and it is taken from the work of Ragatz

(1993). These instances are available on the Inter-

net at https://www.msu.edu/˜rubin/ﬁles/c&ordata.zip.

The job processing times are normally distributed

with a mean of 100 time units and the setup times

are also uniformly distributed with a mean of 9.5 time

units. Each instance has three factors which have both

high and low levels. These factors are due date range,

processing time variance and tardiness factor. The tar-

diness factor determines the expected proportion of

jobs that will be tardy in a random sequence. All the

experiments were run on an Itanium with a 1.4 GHz

processor and 4 GB RAM. Each instance was exe-

cuted 5 times and the results presented represent the

average deviation with the optimal results of Bigras

et al. (2008) . All the algorithms are coded in C++

language under the ILOG IBM CP constraint environ-

ment using ILOG Solver and Scheduler via the C++

API (ILOG, 2003b; ILOG, 2003a).

Table 1 compares the results of different ap-

proaches. In this table, PRB denotes the instance

names and OPT the optimal solution found by the

B&B of Bigras et al. (2008). These authors have not

given information about the execution time of their

approach. They only said that some instances have

been resolved after more than seven days. The GA

column shows the results average deviation to the op-

timal solution of the genetic algorithm described in

the section 3.1 which gives the best results among all

genetic algorithms in the literature without an inten-

siﬁcation process (Sioud et al., 2009). The GA av-

erage CPU time is equal to 13.4 seconds for the 32

instances. The GA generally obtained fairly good re-

sults only for the instances 601, 605, 701 and 705.

These instances are low due date range and large tar-

diness factor. Thus, for this kind of instances, ”good”

solutions may not generate ”good” offspring. Further-

more, considering that the tardy jobs are scheduled at

the end of the sequence, it may be sufﬁcient to sched-

ule the other jobs by minimizing the setup times. It is

the aim of introducing the IP

T SP

intensiﬁcation pro-

cedures.

The CBS column shows the deviations of the CBS

approach minimizing the total tardiness deﬁned in

Section 3.2. For this approach, the execution time

is limited to 60 minutes. It can be noticed that the

CBS approach results deteriorate with increasing the

instances size and especially for the **4, **5 and **8

instances. The GA

PCX

column shows the average de-

ICEC 2010 - International Conference on Evolutionary Computation

142

Table 1: Comparison of different algorithms.

PRB OPT GA CBS GA

PCX

HY B

401 90 0.0 0.0 0.0 0.0 0.0

402 0 0.0 0.0 0.0 0.0 0.0

403 3418 0.5 0.0 0.0 0.4 0.0

404 1067 0.0 0.0 0.0 0.0 0.0

405 0 0.0 0.0 0.0 0.0 0.0

406 0 0.0 0.0 0.0 0.0 0.0

407 1861 0.0 0.0 0.0 0.0 0.0

408 5660 0.2 0.9 0.0 0.1 0.0

501 261 0.5 0.4 0.0 0.5 0.0

502 0 0.0 0.0 0.0 0.0 0.0

503 3497 0.2 2.5 0.0 0.3 0.0

504 0 0.0 0.0 0.0 0.0 0.0

505 0 0.0 0.0 0.0 0.0 0.0

506 0 0.0 0.0 0.0 0.0 0.0

507 7225 0.7 1.8 0.0 0.7 0.0

508 1915 0.0 35.8 0.0 1.8 0.0

601 12 169.4 41.7 6.7 7.5 3.3

602 0 0.0 0.0 0.0 0.0 0.0

603 17587 1.8 6.5 0.8 1.1 0.2

604 19092 1.8 21.1 1.1 1.3 0.6

605 228 13.0 122.4 2.6 3.5 0.4

606 0 0.0 0.0 0.0 0.0 0.0

607 12969 1.6 17.7 0.7 1.9 0.2

608 4732 1.7 156.6 0.7 1.2 0.0

701 97 30.7 20.6 6.8 8.3 2.1

702 0 0.0 0.0 0.0 0.0 0.0

703 26506 1.9 2.8 1.2 1.8 0.9

704 15206 3.4 94.8 1.6 2.1 0.5

705 200 33.7 72.5 6.1 6.5 2.2

706 0 0.0 0.0 0.0 0.0 0.0

707 23789 2.2 20.4 1.0 1.9 0.3

708 22807 2.8 50.0 1.5 2.1 1.2

viation of the genetic algorithm in which the crossover

operator PCX is integrated. The probability p

PCX

equal to 0.2 and the CBS approach execution time is

limited to 15 seconds. The GA

PCX

average time ex-

ecution is equal to 15.2 minutes for the 32 instances.

The ﬁrst observation is that the GA

PCX

algorithm is

always optimal for 15 and 25 jobs instances. It should

be noted that the integration of the PCX crossover im-

proves all of the GA results and especially for the

instances **1 and **5 where the deviation became

less than 7%. For example, the deviation was re-

duced from 169.4% to 6.7% for the 601 instance. Us-

ing the direct precedence constraints allows the PCX

crossover to enhance both the GA exploration and the

CBS search; and consequently reaching better sched-

ules.

The GA

column shows the average deviation of

the genetic algorithm in which we include the IP

Tard

and IP

T SP

intensiﬁcation procedures under probabil-

ity p

equal to 0.1. The CBS approach execution

time is limited to 20 seconds for the IP

Tard

and IP

T SP

The GA

average time execution is equal to 16.5

minutes for the 32 instances. The GA

improves

most GA results and specially the **1 and **5 in-

stances but gives worse results than the GA

PCX

and

this was expected because in 50% of the cases the in-

tensiﬁcation procedure minimizes the makespan and

not the total tardiness.

The GA

HY B

column shows the average deviation

of the GA

PCX

algorithm where we include the IP

Tard

and IP

T SP

intensiﬁcation procedures. The probabil-

ities p

and p

cip

are equal to 0.1 and 0.5 respec-

tively like the GA

. The CBS approach execution

time is also limited to 20 seconds for the IP

Tard

and

T SP

in the GA

HY B

. The GA

HY B

average time exe-

cution is equal to 24.5 minutes for the 32 instances.

This hybrid algorithm improves all the results found

by the GA

PCX

. These improvements are more pro-

CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING

PROBLEM WITH SEQUENCE-DEPENDENT SETUP TIMES

143

nounced with the integration of local search proce-

dures. The introduction of the two intensiﬁcation pro-

cedures improves essentially the **1 and the **5 in-

stances. Also, the optimal schedule is always reached

by GA

HY B

for the 608 instance. The GA

HY B

found

the optimal solution for all the instances at least one

time and this was not the case either for GA

PCX

The convergence of both GA and the GA

PCX

al-

gorithms are similar. Indeed, the average conver-

gence generation is equal to 1837 and 1845 genera-

tions for GA and GA

PCX

, respectively. Concerning

the GA

algorithm, the average convergence gener-

ation is equal to 1325 generations. So, we can con-

clude that the two intensiﬁcation procedures based

on the CBS approach are permitting a faster genetic

algorithm convergence than the PCX crossover but

achieving worse results. The GA

HY B

average conver-

gence generation is equal to 825 and compared to the

PCX

, the introduction of the intensiﬁcation proce-

dures speeds up the convergence of the solution with

reaching better results.

Exact methods are well known to be time ex-

pensive. The same applies to their hybridization of

them with metaheuristics. Indeed, times execution in-

creases signiﬁcantly with such hybridization policies

due to some technicality during the exchange of infor-

mation between the two methods (Talbi, 2009; Talbi,

2002; Puchinger and Raidl, 2005; Jourdan et al.,

2009) and this is what has been observed here. How-

ever, in this paper, the solution quality is our main

concern. So, we concentrated our efforts on it.

5 CONCLUSIONS

In this paper, we describe the hybridization into a

Genetic Algorithm of both a crossover operator and

intensiﬁcation process based on Constraint Based

Scheduling. The PCX crossover operator uses the

direct precedence constraints to improve the CBS

search and consequently the schedules quality. The

precedence constraints are built from the selected par-

ents information in the reproduction process.

The intensiﬁcation procedures are based on two

different CBS approaches after ﬁxing a jobs block :

the ﬁrst minimizes the total tardiness which represents

the considered problem objective function while the

second minimizes the makespan which also enhances

the exploration process and is well adapted to some

instances. These three policies hybridization repre-

sent the main contribution of this paper.

Compared to a simple GA, the use of the PCX

crossover improves all the results but for some in-

stances the difference is still noticeable. The hybrid

algorithm which uses the PCX crossover and the in-

tensiﬁcation process improves the results and speeds

up the convergence of the solution. These results sug-

gest that the latter model seems to outperform the sin-

gle GA, the genetic algorithm with the hybrid PCX

crossover and the genetic algorithm with the intensi-

ﬁcation process.

A possible area of research in the future would

be to improve the precedence constraints quality. In-

deed, it is possible to consider constraints related to

a jobs set or to intervals time and indirect constraint.

Another possible area for further research would be

to employ a chromosome representation based on the

start times of activities. Hence, it will be possible to

get more accurate combination of start times.

REFERENCES

Allahverdi, A., Ng, C., Cheng, T., and Kovalyov, M. Y.

(2008). A survey of scheduling problems with setup

times or costs. European Journal of Operational Re-

search, 187(3):985 – 1032.

Armentano, V. and Mazzini, R. (2000). A genetic algo-

rithm for scheduling on a single machine with setup

times and due dates. Production Planning and Con-

troly, 11(7):713 – 720.

Baptiste, P., LePape, C., and Nuijten, W. (2001).

Constraint-Based Scheduling : Applying Constraint

Programming to Scheduling Problems. Kluwer Aca-

demic Publishers.

Beck, J. C. and Perron, L. (2000). Discrepancy bounded

depth ﬁrst search. In CP-AI-OR’2000: Fourth Inter-

national Workshop on Integration of AI and OR Tech-

niques in Constraint Programming for Combinatorial

Optimization Problems, pages 7–17.

Bierwirth, C., Mattfeld, D. C., and Kopfer, H. (1996). On

permutation representations for scheduling problems.

In PPSN IV: Proceedings of the 4th International

Conference on Parallel Problem Solving from Nature,

pages 310–318, London, UK. Springer-Verlag.

Bigras, L., Gamache, M., and Savard, G. (2008). The time-

dependent traveling salesman problem and single ma-

chine scheduling problems with sequence dependent

setup times. Discrete Optimization, 5(4):663–762.

Du, J. and Leung, J. Y. T. (1990). Minimizing total tar-

diness on one machine is np-hard. Mathematics and

Operations Researchs, 15:438–495.

Franca, P. M., Mendes, A., and Moscato, P. (2001). A

memetic algorithm for the total tardiness single ma-

chine scheduling problem. European Journal of Op-

erational Research, 132:224–242.

Fromherz, M. P. (1999). Model-based conﬁguration of ma-

chine control software. Technical report, In Conﬁgu-

ration Papers from the AAAI Workshop.

ICEC 2010 - International Conference on Evolutionary Computation

144

Gagn

e, C., Gravel, M., and Price, W. L. (2005). Using meta-

heuristic compromise programming for the solution of

multiple objective scheduling problems. The Journal

of the Operational Research Society, 56:687–698.

Gagn

e, C., Price, W., and Gravel, M. (2002). Comparing an

aco algorithm with other heuristics for the single ma-

chine scheduling problem with sequence-dependent

setup times. Journal of the Operational Research So-

ciety, 53:895–906.

Graham, R. L., Lawler, E. L., Lenstra, J. K., and Kan, A. G.

H. R. (1979). Optimization and approximation in de-

terministic sequencing and scheduling: a survey. An-

nals of Discrete Mathematics, 5:287–326.

Gupta, S. R. and Smith, J. S. (2006). Algorithms for sin-

gle machine total tardiness scheduling with sequence

dependent setups. European Journal of Operational

Research, 175(2):722–739.

Holland, J. H. (1992). Adaptation in natural and artiﬁcial

systems. MIT Press, Cambridge, MA, USA.

ILOG (2003a). ILOG Scheduler 6.0. User Manual. ILOG.

ILOG (2003b). ILOG Solver 6.0. User Manual. ILOG.

Jourdan, L., Basseur, M., and Talbi, E.-G. (2009). Hy-

bridizing exact methods and metaheuristics: A tax-

onomy. European Journal of Operational Research,

199(3):620–629.

Lee, Y., Bhaskaram, K., and Pinedo, M. (1997). A

heuristic to minimize the total weighted tardiness with

sequence-dependent setups. IIE Transactions, 29:45–

52.

Liao, C. and Juan, H. (2007). An ant colony opti-

mization for single-machine tardiness scheduling with

sequence-dependent setups. Computers and Opera-

tions Research, 34:1899–1909.

Meseguer, P. (1997). Interleaved depth-ﬁrst search. In

IJCAI’97: Proceedings of the Fifteenth international

joint conference on Artiﬁcal intelligence, pages 1382–

1387, San Francisco, CA, USA. Morgan Kaufmann

Publishers Inc.

Michalewicz, Z. (1996). Genetic algorithms + data struc-

tures = evolution programs (3rd ed.). Springer-Verlag,

London, UK.

Pinedo, M. (2002). Scheduling Theory, Algorithm and Sys-

tems. Prentice-Hall.

Puchinger, J. and Raidl, G. R. (2005). Combining meta-

heuristics and exact algorithms in combinatorial opti-

mization: A survey and classiﬁcation. In Proceedings

of the First International Work-Conference on the In-

terplay Between Natural and Artiﬁcial Computation,

Las Palmas, Spain, LNCS.

Ragatz, G. L. (1993). A branch-and-bound method for

minimumtardiness sequencing on a single processor

with sequence dependent setup times. In Proceedings

twenty-fourth annual meeting of the Decision Sciences

Institute, pages 1375–1377.

Rubin, P. and Ragatz, G. (1995). Scheduling in a sequence-

dependent setup environment with genetic search.

Computers and Operations Research, 22:85–99.

Sioud, A., Gravel, M., and Gagn

e, C. (2009). New

crossover operator for the single machine schedul-

ing problem with sequence-dependent setup times. In

GEM’09: The 2009 International Conference on Ge-

netic and Evolutionary Methods.

Spina, R., Galantucci, L., and Dassisti, M. (2003). A hy-

brid approach to the single line scheduling problem

with multiple products and sequence-dependent time.

Computers and Industrial Engineering, 45(4):573 –

583.

Talbi, E. (2002). A taxonomy of hybrid metaheuristics.

Journal of Heuristics, 8:541–564.

Talbi, E.-G. (2009). Metaheuristics : from design to imple-

mentation. John Wiley & Sons.

Tan, K. and Narasimhan, R. (1997). Minimizing tardi-

ness on a single processor with setup-dependent setup

times: a simulated annealing approach. Omega,

25:619 – 634.

Walsh, T. (1997). Depth-bounded discrepancy search. In

IJCAI’97: Proceedings of the Fifteenth international

joint conference on Artiﬁcal intelligence, pages 1388–

1393, San Francisco, CA, USA. Morgan Kaufmann

Publishers Inc.

Yunes, T., Aron, I. D., and Hooker, J. N. (2010). An Inte-

grated Solver for Optimization Problems. Operations

Resaearch, 58(2):342–356.

CONSTRAINT BASED SCHEDULING IN A GENETIC ALGORITHM FOR THE SINGLE MACHINE SCHEDULING

PROBLEM WITH SEQUENCE-DEPENDENT SETUP TIMES

145