THEOREM PROVING IN THE ONTOLOGY LIFECYCLE

Megan Katsumi and Michael Gr¨uninger

Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, Ontario, Canada

Keywords:

Ontology design, Veriﬁcation, Theorem proving, First-order logic.

Abstract:

In this paper we present a methodology for the veriﬁcation of ﬁrst-order logic ontologies, and provide a

lifecycle in which it may be implemented to develop a correct ontology. We discuss the need for a methodology

to address development issues and illustrate the way in which this characterization of the ontology lifecycle

supports the design and deployment of ontologies within software applications. Theorem proving plays a

critical role in the speciﬁcation of requirements, design, and veriﬁcation of the ontology. We illustrate the

application of theorem proving in the lifecycle using examples from the PSL Ontology.

1 INTRODUCTION

The design of ontologies is a complicated process,

and there has been much work in the literature de-

voted to the development of methodologies to assist

the ontology engineer in this respect. In this paper

we present an approach to the semiautomatic veriﬁ-

cation of ﬁrst-order logic ontologies, and describe a

lifecycle in which it may be implemented to develop

a correct ontology. Our objective is not to propose

a new ontology development methodology, but rather

to use theorem proving as the basis for formally deﬁn-

ing the steps within our methodology and their rela-

tionships to a notion of veriﬁcation that focuses on

the model-theoretic properties of the ontology. Al-

though the ontology lifecycle described in this paper

was developed to address issues that arise as a result

of the semidecidable nature of ﬁrst-order logic, the

methodology and lifecycle is applicable to automated

reasoning with less expressive languages.

We will discuss some existing methodologies for

ontology development, and provide motivation for the

methodology presented here. This work is a result of

experiences in the development of an extension of the

PSL ontology (Bock and Gr¨uninger, 2004; Gr¨uninger,

2009b) that is sufﬁcient to represent ﬂow modelling

notations such as UML, BPMN, and IDEF3. We

therefore provide a brief overview of the PSL ontol-

ogy, which will provide context for the examples of

the ontology lifecycle. The focus of the paper will be

a discussion of the role that theorem proving plays in

each phase of the lifecycle, with an emphasis on prag-

matic guidance for the semiautomatic veriﬁcation of

ontologies.

2 ONTOLOGY DEVELOPMENT

IN LITERATURE

High-level methodologies for ontology development

tend to cover the breadth of the development process,

however they do not provide techniques at the more

detailed level. The On-To-Knowledge Management

(OTKM) (Sure et al., 2003) methodology covers the

full lifecycle of ontology development. It provides

useful insights into the steps required both pre- and

post- application, but it does not provide exact details

on how activities like testing should be performed, or

what is to be done if an ontology fails to satisfy a

requirement. METHONTOLOGY (Fern´andez et al.,

1997) covers areas of the lifecycle similar to what is

presented in the OTKM methodology, with a focus

on the explanation of the concepts at each stage in de-

velopment. DILIGENT (Pinto et al., 2003) provides

guidance to support the distributed (geographically or

organizationally) development of ontologies; in par-

ticular, the authors present a method to enable the

adaptation of an ontology from different parties.

Low-level ontology design methodologiesprovide

detailed instruction, concentrating on means to ac-

complish some necessary step in ontology develop-

ment. The methodology that was used in the de-

sign of the TOVE Ontology for enterprise modelling

(Gr¨uninger and Fox, 1995) introduced the notion of

competency questions to deﬁne the requirements of

an ontology and to guide the formal deﬁnition of a

set of axioms for the ontology. The Enterprise On-

tology (Uschold and King, 1995), also arising from

work with enterprise ontologies, presents an approach

Katsumi M. and Grüninger M..

THEOREM PROVING IN THE ONTOLOGY LIFECYCLE.

DOI: 10.5220/0003076400370049

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2010), pages 37-49

ISBN: 978-989-8425-29-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

for ontology capture that emphasizes the notion of

“middle-out” design, givingequal weight to top-down

issues (such as requirements) and bottom-up issues

(such as reuse).

The evaluation of an ontology is generally ac-

cepted as a key process in its development. The

main efforts in this area focus on taxonomy evalua-

tion (G´omez-P´erez et al., 2004); to the best of our

knowledge, there have been no efforts towards evalu-

ation methodologies that are semantically deeper than

this. This is possibly due to the issue of semidecid-

ability ﬁrst-order logic and the inherent intractability

of theorem provers that presents a challenge for the

evaluation of test results. High level methodologies

typically do not specify the requirements in a veriﬁ-

able form. In any case, the existing methodologies do

not sufﬁciently address the issue of ontology veriﬁca-

tion, and our goal is to address this hole, in particular,

the challenges encountered in ﬁrst-order logic devel-

opment.

3 CASE STUDY: AN ONTOLOGY

FOR FLOW MODELLING

The motivating scenarios which initiated this work

and which will be used to illustrate the different

phases of the ontology lifecycle are based on an ef-

fort to provide a process ontology for ﬂow modelling

formalisms such as UML activity diagrams, BPMN,

and IDEF3. For example, consider the UML activity

diagram in Figure 1; any process ontology that cap-

tures the intended semantics of such a diagram needs

to be able represent the constraints that are implicit in

the notions of split/merge and fork/join nodes. Intu-

itively, there are three possible ways in which the pro-

cess described by the activity diagram can occur; in

all three occurrences of the process, there is an initial

occurrence of the subactivity A and a ﬁnal occurrence

of the subactivity E. One occurrence of the process

contains an occurrence of the subactivity F, while the

other two contain occurrences of the subactivities B,

C, and D. In order to developsuch an ontology, we be-

gan with the Process Speciﬁcation Language (PSL),

but in order to capture the intended semantics of the

UML constructs, we also needed to develop an exten-

sion to the ontology that explicitly captured the asso-

ciated ordering and occurrence constraints.

In this section, we give a brief introduction of the

PSL Ontology and an overviewof the relations for the

extension to the PSL Ontology. Throughout the re-

mainder of the paper, we will follow the development

of this extension from the speciﬁcation of the initial

requirements to the veriﬁcation of the proposed ax-

Figure 1: Example of a UML activity diagram.

iomatization.

3.1 The PSL Ontology

The Process Speciﬁcation Language (PSL) (Bock

and Gr¨uninger, 2004; Gr¨uninger, 2009b; Gr¨uninger,

2003) has been designed to facilitate correct and com-

plete exchange of process information.

The primary

purpose of PSL is to enable the semantic interop-

erability of manufacturing process descriptions be-

tween manufacturing engineering and business soft-

ware applications such as process planning, schedul-

ing, workﬂow, and project management. Additional

applications of PSL include business process design

and analysis, the implementation of business pro-

cesses as web services, and enterprise modelling.

The PSL Ontology is a modular set of theories

in the language of ﬁrst-order logic. All core theo-

ries within the ontology are consistent extensions of

a theory referred to as PSL-Core, which introduces

the basic ontological commitment to a domain of ac-

tivities, activity occurrences, timepoints, and objects

that participate in activities. Additional core theories

capture the basic intuitions for the composition of ac-

tivities, and the relationship between the occurrence

PSL has been published as an International Standard

(ISO 18629) within the International Organisation of Stan-

dardisation. The full set of axioms (which we call T

psl

)

in the Common Logic Interchange Format is available at

http://www.mel.nist.gov/psl/ontology.html.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

of a complex activity and occurrences of its subactiv-

ities.

In order to formally specify a broad variety of

properties and constraints on complex activities, we

need to explicitly describe and quantify over com-

plex activities and their occurrences. Within the

PSL Ontology, complex activities and occurrences

of activities are elements of the domain and the

occurrence of relation is used to capture the relation-

ship between different occurrences of the same activ-

ity.

A second requirement for formalising queries is

to specify composition of activities and occurrences.

The PSL Ontology uses the subactivity relation to

capture the basic intuitions for the composition of ac-

tivities. Complex activities are composed of sets of

atomic activities, which in turn are either primitive

(i.e., they have no proper subactivities) or they are

concurrent combinations of primitive activities.

Corresponding to the composition relation over

activities, subactivity occurrence is the composition

relation over activity occurrences. Given an occur-

rence of a complex activity, subactivity occurrences

are occurrences of subactivities of the complex activ-

ity.

Finally, we need some way to specify order-

ing constraints over the subactivity occurrences of

a complex activity. The PSL Ontology uses the

min precedes(s

, s

, a) relation to denote that subac-

tivity occurrence s

precedes the subactivity occur-

rence s

in occurrences of the complex activity a.

Note that there could be other subactivity occurrences

between s

and s

. We use next subocc(s

, s

, a) to

denote that s

is the next subactivity occurrence after

in occurrences of the complex activity a.

The basic structure that characterises occurrences

of complex activities within models of the ontology

is the activity tree, which is a subtree of the legal oc-

currence tree that consists of all possible sequences

of atomic subactivity occurrences of an activity; the

relation root(s, a) denotes that the subactivity occur-

rence s is the root of an activity tree for a. Elements

of the tree are ordered by the min precedes relation;

each branch of an activity tree is a linearly ordered set

of occurrences of subactivities of the complex activ-

ity. The same tree(s

, s

, a) is used to denote that s

and s

are both elements of the same activity tree for

a. Finally, there is a one-to-one correspondence be-

tween occurrences of complex activities and branches

of the associated activity trees.

In a sense, an activity tree is a microcosm of the

occurrence tree, in which we consider all of the ways

in which the world unfolds in the context of an oc-

currence of the complex activity. Different subactiv-

ities may occur on different branches of the activity

tree — different occurrences of an activity may have

different subactivity occurrences or different order-

ings on the same subactivity occurrences. The rela-

tion mono(s

, s

, a) indicates that s

and s

are occur-

rences of the same subactivity on different branches

of the activity tree for a.

3.2 Subactivity Occurrence Orderings

The approach taken in the development of the new

extension to the PSL Ontology is to represent ﬂow

models such as UML activity diagrams as a partial

ordering over a set of subactivity occurrences. This

partial ordering is embedded into an activity tree such

that the branches of the activity tree correspond to a

set of linear extensions for suborderings of the partial

ordering. For example, the subactivity occurrence or-

dering corresponding to the UML activity diagram in

Figure 1 can be found in Figure 2, while the activity

tree into which this partial ordering is embedded can

be found in Figure 3.

Figure 2: Example of a subactivity occurrence ordering.

Three relations are introduced to specify the rela-

tionship between the partial ordering (referred to as

the subactivity occurrence ordering) and the activ-

ity tree. The relation soo(s, a) denotes that the ac-

tivity occurrence s is an element of the subactivity

occurrence ordering for the activity a. The relation

soo precedes(s

, s

, a) captures the ordering over the

elements. For example

, the partial ordering in Figure

2 can be deﬁned by:

soo(o

, a) ∧ soo(o

, a), soo(o

, a) ∧ soo(o

, a)

∧ soo(o

, a) ∧ soo(o

, F) ∧ soo precedes(o

, o

, a)

∧ soo precedes(o

, o

, a) ∧ soo precedes(o

, o

, a)

Each activity occurrence is an occurrence of a unique

activity but activities can have multiple occurrences, so we

label activity occurrences using the following convention:

for activity occurrence o

, i is a unique label for the occur-

rence and j denotes the activity of which it is an occurrence.

For example, o

and o

are two occurrences of the activity

THEOREM PROVING IN THE ONTOLOGY LIFECYCLE

∧ soo precedes(o

, o

, a) ∧ soo precedes(o

, o

, a)

∧ soo precedes(o

, o

, a) ∧ soo precedes(o

, o

, a)

(1)

and the activity tree in Figure 3 can be speciﬁed by

min precedes(o

, o

, a) (2)

∧ min precedes(o

, o

, a) ∧ min precedes(o

, o

, a)

∧ min precedes(o

, o

, a) ∧ min precedes(o

, o

, a)

∧ min precedes(o

, o

, a) ∧ min precedes(o

, o

, a)

∧ min precedes(o

, o

, a) ∧ min precedes(o

, o

, a)

Two branches of the activity tree correspond

to linear extensions of the subordering of the par-

tial ordering in Figure 2 consisting of the elements

, o

} while the remaining branch corre-

sponds to the subordering consisting of the elements

, o

Finally, the preserves(s

, s

, a) relation

holds whenever the mono relation preserves the

min precedes relation; that is, if s

min precedes

, then there is no element of the activity tree that

is mono to s

that min precedes an element of the

activity tree that is mono to s

Figure 3: An activity tree corresponding to the subactivity

occurrence ordering in Figure 2.

The complete set of axioms for the subactivity oc-

currence ordering extension to the PSL Ontology can

be found in Appendix A.

4 THE ONTOLOGY LIFECYCLE

The lifecycle presented in Figure 4 is intended to

serve as a structured framework that provides guid-

ance during the ontology development process. This

lifecycle addresses the limitations of existing veriﬁ-

cation techniques while providing a structure within

which existing techniques for ontology design and re-

quirements identiﬁcation may be applied. The feed-

back and interactions between the various phases il-

lustrates the tight integration between the design and

the veriﬁcation of the ontology. Throughout this sec-

tion, we illustrate the efﬁcacy of this lifecycle frame-

work using examples from the design and mainte-

nance of the PSL Ontology.

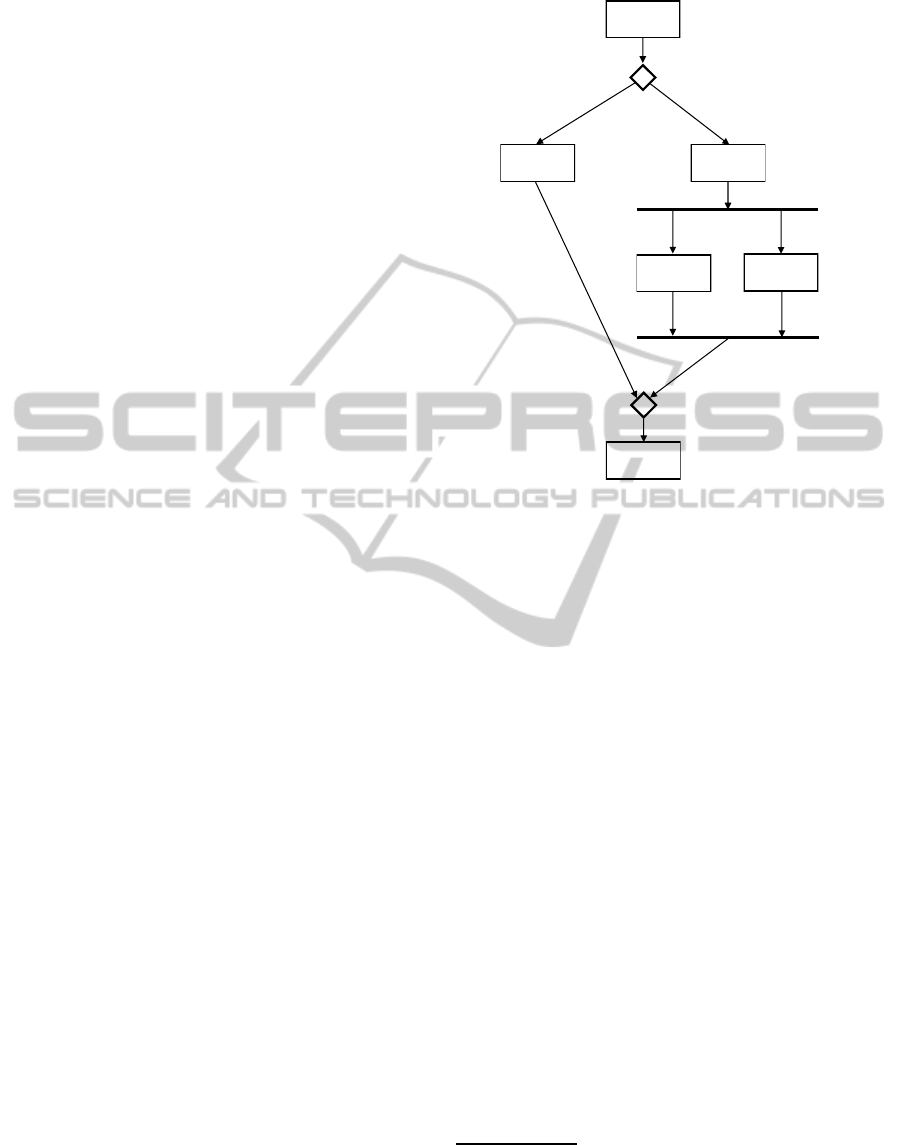
Figure 4: The Ontology Lifecycle.

We deﬁne ﬁve phases in the ontology lifecycle:

• The Requirements Phase produces a speciﬁcation

of the intended models of the ontology arising

from a set of use cases (also referred to as motivat-

ing scenarios in (Uschold and Gr¨uninger, 1996))

• The Design Phase produces an ontology to axiom-

atize the class of models that capture the require-

ments. The feedback loop that is shown in Fig-

ure 4 between the Design Phase and the Require-

ments Phase occurs as the ontology develops. In

the Requirements Phase the intended models must

initially be speciﬁed informally, until the design

of the ontology has matured such that its require-

ments may be speciﬁed using its vocabulary.

• The Veriﬁcation Phase guarantees that the in-

tended models of the ontology which are speci-

ﬁed in the Requirements Phase are equivalent to

the models of the axioms which are produced in

the Design Phase.

• The Tuning Phase addresses the pragmatic is-

sue of dealing with cases in which the theorem

provers used in the Veriﬁcation Phase fail to re-

turn a deﬁnitive answer.

• The Application Phase covers the different ways

in which the ontology is used, such as decision

support systems, semantic integration, and search.

Each phase in the ontology lifecycle is associated

with a set of reasoning problems that are deﬁned with

respect to the axioms of the ontology T

onto

, a domain

theory Σ

domain

that uses the ontology, and a query

Φ that formalizes the competency questions and On-

tological Stance scenarios produced in the Require-

ments Phase. Since these reasoning problems are en-

tailment problems of the form:

onto

∪ Σ

domain

|= Φ

we can utilize theorem provers to verify that the ax-

iomatization of the ontology satisﬁes its requirements.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

The relationships between the stages of the ontology

lifecycle and the different aspects of the reasoning

problems are shown in Figure 5.

The Design Phase provides the axioms T

onto

∪

domain

that form the antecedent of the reasoning

problem. In the Veriﬁcation Phase, we use theorem

provers to determine whether or not the sentences that

capture the requirements are indeed entailed by the

axioms of the ontology.

Design

z }| {

onto

∪ Σ

domain

Requirements

z}|{

| {z }

Verification

Figure 5: Reasoning problems and stages of the ontology

lifecycle.

4.1 Requirements

Requirements for an ontology are speciﬁed with re-

spect to the intended semantics of the terminology,

and the challenge of the initial phase of the ontology

lifecycle is to cast these requirements in a testable

form. From a mathematical perspective the require-

ments may be characterized by their intended models

(Section 4.1.1); to allow for semiautomatic veriﬁca-

tion we specify these semantic requirements as en-

tailment problems, with the use of competency ques-

tions (Section 4.1.2) or the Ontological Stance (Sec-

tion 4.1.3). From a reasoning problem perspective the

output of the Requirements Phase is a set of conse-

quents for the entailment problems described above.

4.1.1 Intended Models

In current ontology research, the languages for for-

mal ontologies (such as RDFS, OWL, and Common

Logic) are closely related to mathematical logic, in

which the semantics are based on the notion of an in-

terpretation. If a sentence is true in the interpretation,

we say that the sentence is satisﬁed by the interpreta-

tion. If every axiom in the ontology is satisﬁed by the

interpretation, then the interpretation is called a model

of the ontology. With a formal ontology, the content

of the ontology is speciﬁed as a theory, so that a sen-

tence is consistent with that theory if there exists a

model of the theory that satisﬁes the sentence; a sen-

tence can be deduced if it is satisﬁed by all models of

the theory. Therefore, the semantics of the ontology’s

terminology can be characterized by this implicit set

of models, which we refer to as the set of intended

models.

Intended models are speciﬁed with respect to

some well-understood class of mathematical struc-

tures (such as partial orderings, graph theory, and ge-

ometry). The extensions of the relations in the model

are then speciﬁed with respect to properties of these

mathematical structures.

For example, the intended models for the subac-

tivity occurrence ordering extension to the PSL On-

tology are intuitively speciﬁed by two properties:

• the partial ordering over the subactivity occur-

rences;

• the mapping that embeds the partial ordering into

the activity tree.

Formally, the intended models for the subactivity oc-

currence ordering extension are deﬁned by

Deﬁnition 1. Let M

soo

be the following class of

structures such that for any M ∈ M

soo

1. M is an extension of a model of T

psl

(i.e. the PSL

Ontology);

2. for each activity tree τ

, there exists a unique par-

tial ordering ρ

= (P

, ≺) and a mapping

θ : τ

→ ρ

such that

(a) hs

, s

, ai ∈ min precedes ⇒ θ(s

) 6≺ θ(s

)

(b) hθ(s), s, ai ∈ mono;

parable elements in τ.

3. hs, ai ∈ soo iff s ∈ P

;

4. hs

, s

, ai ∈ soo precedes iff s

≺ s

Although one can take this approach to explicitly

specify the intended models as a class of mathemat-

ical structures, in practice the speciﬁcation of the in-

tended models is based on use cases for the applica-

tion of the ontology. The two primary application ar-

eas for the PSL Ontology have been in semantic in-

tegration and decision support systems. In this ap-

proach, the intended models are deﬁned implicitly

with respect either to the set of sentences that are

satisﬁed by all of the intended models or to sets of

sentences that should be satisﬁed by some model. If

we recall that sentences satisﬁed by all models are

entailed by the axiomatization, then this leads us to

the idea of implicitly deﬁning the intended models of

the ontology with respect to reasoning problems. The

reasoning problems that are associated with the Re-

quirements Phase are competency questions (which

arise primarily from decision support use cases) and

Ontological Stance scenarios (which are motivated by

semantic integration use cases).

4.1.2 Competency Questions

Following (Gr¨uninger and Fox, 1995; Gruninger and

Fox, 1994; Uschold and Gr¨uninger, 1996), compe-

THEOREM PROVING IN THE ONTOLOGY LIFECYCLE

tency questions are queries that impose demands on

the expressiveness of the underlying ontology. Intu-

itively, the ontology must be able to represent these

questions and characterize the answers using the ter-

minology. The relationship between competency

questions and the requirements is that the associated

query must be provable from the axioms of the ontol-

ogy alone. Since a sentence is provable if and only if

it is satisﬁed by all models, competency questions im-

plicitly specify the intended models of the ontology.

In the area of decision support, the veriﬁcation of

an ontology allows us to make the claim that any in-

ferences drawn by a reasoning engine using the ontol-

ogy are actually entailed by the ontology’s intended

models. If an ontology’s axiomatization has unin-

tended models, then it is possible to ﬁnd sentences

that are entailed by the intended models, but which

are not provable from the axioms of the ontology.

Examples of competency questions for the subac-

tivity occurrence ordering extension include the fol-

lowing:

Which subactivities can possibly occur next after

an occurrence of the activity a

(∀o, s

) occurrence(s

, a

) ∧ occurrence(o, a) (3)

∧ subactivity occurrence(s

, o)

⊃ (∃a

, s

) occurrence(s

, a

) ∧ next subocc(s

, s

, a))

Does there exist a point in an activity tree for a

after which the same subactivities occur?

(∃a, a

, s

) subactivity(a

, a) ∧ occurrence of(s

, a

)

∧ ((∀o

, o

) occurrence of (o

, a) ∧ occurrence of(o

, a)

∧ subactivity occurrence(s

, o

)

∧ subactivity occurrence(s

, o

)

∧ min precedes(s

, s

, a)

⊃ (∃s

) subactivity occurrence(s

, o

)

∧ min precedes(s

, s

, a) ∧ mono(s

, s

, a) (4)

Recall that sentences such as these constitute the

consequent Φ of a reasoning problem (see Figure 5),

and that they are supposed to be entailed by the ax-

ioms of the ontology T

onto

together with a domain the-

ory T

domain

(which in this case is a process description

that formalizes a speciﬁc UML activity diagram). It

is in this sense that competency questions are require-

ments for the ontology – there must be sufﬁcient ax-

ioms in T

onto

∪ T

domain

to entail the sentences that for-

malize the competency questions.

4.1.3 Ontological Stance

We can say that two software systems are semanti-

cally integrated if their sets of intended models are

equivalent. However, systems cannot exchange the

models themselves – they can only exchange sen-

tences in the formal language that they use to repre-

sent their knowledge. We must be able to guarantee

that the inferences made with sentences exchanged in

this way are equivalent to the inferences made with

respect to the system’s intended models – given some

input the application uses these intended models to

infer the correct output. This leads to the notion of

the Ontological Stance (Gr¨uninger, 2009a) in which a

software application is described as if it were an in-

ference system with an axiomatized ontology which

is used to predict the set of sentences that the infer-

ence system decides to be satisﬁable. What is of rele-

vance for the ontologylifecycle is that the Ontological

Stance does not directly postulate a speciﬁc set of ax-

ioms, but rather a set of intended models: Given an

application A, there exists a class of models M

such

that any sentence Φ is decided by A to be satisﬁable

if and only if there exists a model M ∈ M such that

M entails Φ.

In the context of the subactivity occurrence order-

ing extension to the PSL Ontology, software appli-

cations that simulate ﬂow modelling diagrams such

as UML or IDEF3 form the basis of the Ontologi-

cal Stance scenarios. Reasoning problems associated

with such software applications typically involve ex-

ecutability – a particular execution of the process a

involving some subactivity a

is a possible output of

the software application if and only if the following

sentence is entailed:

(∀o) occurrence(o, a) ⊃ (∃s) occurrence(s, a

)

∧ subactivity occurrence(s, o) (5)

As we saw earlier with competency questions, this

sentence constitutes the consequent of the reasoning

problem that will be the focus of the Veriﬁcation

Phase (see Figure 5). The antecedent for the rea-

soning problem that corresponds to the Ontological

Stance is slightly different – T

onto

is the axiomatiza-

tion of the ontology for the software application while

domain

is the axiomatization of the input to the soft-

ware application.

4.2 Design

As we saw in Figure 5, the Design Phase produces

a set of axioms that is supposed to entail the com-

petency questions and Ontological Stance scenarios.

We do not prescribe a speciﬁc methodology for the

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

design of the axioms; rather the reasoning problems

associated with the Design Phase focus on the notion

of the design rationale for axioms. The task in this

case to characterize why speciﬁc axioms are required,

tracing each axiom back to the original set of require-

ments for the ontology.

4.3 Veriﬁcation

As we saw earlier, existing approaches to ontology

veriﬁcation focus on taxonomic relationships and ob-

vious logical criteria for ontology evaluation such as

consistency. Strictly speaking, we only need to show

that a model exists in order to demonstrate that a

ﬁrst-order theory is consistent. Constructing a sin-

gle model, however, runs the risk of having demon-

strated satisﬁability for a restricted case; for example,

one could construct a model of a process ontology in

which no processes occur, without realizing that the

axiomatization might mistakenly be inconsistent with

any theory in which processes do occur. We therefore

need a complete characterization of all models of the

ontology up to isomorphism.

In general, veriﬁcation is concerned with the rela-

tionship between the intended models of an ontology

and the models of the axiomatization of the ontology.

From a mathematical perspective this is formalized

by the notion of representation theorems. From a rea-

soning problem perspective this amounts to evaluat-

ing the entailment problems, and we are able to per-

form this veriﬁcation semiautomatically with the use

of a theorem prover.

4.3.1 Representation Theorems

Representation theorems are proven in two parts – we

ﬁrst prove every structure in the class is a model of

the ontology and then prove that every model of the

ontology is elementary equivalent to some structure

in the class.

For the new extension T

soo

to the PSL Ontology,

the representation theorem is stated as follows:

Theorem 1. Any structure M ∈ M

soo

is isomorphic

to a model of T

soo

∪ T

psl

Any model of T

soo

∪ T

psl

is isomorphic to a struc-

ture in M

soo

The characterization up to isomorphism of the

models of an ontology through a representation theo-

rem has several distinct advantages. First, unintended

models are more easily identiﬁed, since the represen-

tation theorems characterize all models of the ontol-

ogy. We also gain insight into any implicit assump-

tions within the axiomatization which may actually

eliminate models that were intended. Second, any de-

cidability and complexityresults that have been estab-

lished for the classes of mathematical structures in the

representation theorems can be extended to the ontol-

ogy itself. Finally, the characterization of models sup-

ports the speciﬁcation of semantic mappings to other

ontologies, since such mappings between ontologies

preserve substructures of their models.

Representation theorems are distinct from the no-

tion of the completeness of an ontology. A logical

theory T is complete if and only if for any sentence

Φ, either T |= Φ or T 6|= Φ. The ontologies that we

develop are almost never complete in this sense. Nev-

ertheless, we can consider representation theorems to

be demonstration that the ontology T

onto

is complete

with respect to its requirements (i.e. set of intended

models M

onto

). This allows us to say that T

onto

|= Φ

if and only if M

onto

|= Φ (that is, the ontology entails

a sentence if and only if the class of intended models

entails the sentence).

The typical way to prove the Representation Theo-

rem for an ontology is to explicitly construct the mod-

els of the ontology in the metatheory and then show

that these models are equivalent to the speciﬁcation

of the intended models of the ontology using classes

of mathematical structures. As we saw with the spec-

iﬁcation of the intended models, an alternative to the

mathematical speciﬁcation of the representation the-

orem is to employ a theorem prover to verify that the

models of the ontology are equivalent to the intended

models. Rather than proving the Representation The-

orem directly, we can utilize the speciﬁcation of the

requirements for the ontology as competency ques-

tions and Ontological Stance scenarios. We can do

this by proving that the extensions of the relations in

the models of the ontology have properties that are

equivalent to those satisﬁed by the extensions of the

relations in the intended models. For example, the

subactivity occurrence ordering ρ introduced in the

deﬁnition of the intended models M

soo

is a partial or-

dering, and this corresponds to the competency ques-

tions which asserts that the soo precedes relation is

also a partial ordering, and hence is a transitive rela-

tion:

(∀s

, s

, a) soo precedes(s

, s

, a) (6)

∧ soo precedes(s

, s

, a) ⊃ soo precedes(s

, s

, a)

This illustrates the technique of identifying com-

petency questions directly from the mathematical def-

inition of the intended models.

THEOREM PROVING IN THE ONTOLOGY LIFECYCLE

4.3.2 Outcomes of Veriﬁcation

As we have just seen, the reasoning problems as-

sociated with Veriﬁcation support the proofs of the

Representation Theorem. In addition to the compe-

tency questions, this also involves proving proposi-

tions which demonstrate that the extensions of the re-

lations in the models of the ontology have the same

properties as the extensions of relations in the in-

tended models.

For a test of any given requirement, there are three

possible outcomes of the Veriﬁcation Phase:

Case 1: Unintended Proof Found. In this case, a

proof was found of a sentence that contradicts the

intended semantics of the ontology. This is of-

ten encountered when the theorem prover ﬁnds

a proof without using all, or any clauses from

the proposition or query. Given this possibility,

a thorough inspection of all proofs found must be

performed; if this case is detected, it is indicative

of at least one of two possible errors with the on-

tology:

1. An examination of the proof may lead to the

identiﬁcation of some axiom in the ontology

which is not entailed by the intended models;

in this case we must return to the Design Phase.

One such result with the design of the sub-

activity occurrence ordering extension T

soo

the PSL ontology arose when testing its consis-

tency with the ﬁrst addition of T

soo

. A proof

was found, and normally this would indicate

an error in the set of deﬁnitions that was be-

ing tested. However, upon examination we re-

alized that the deﬁnition of the same tree rela-

tion made it inconsistent for any model of the

ontology to have an occurrence in the same ac-

tivity tree as the root of the tree:

soo

∪ T

psl

|= (∀s

, a) root(s

, a)

⊃ ¬(∃s

) same tree(s

, s

, a) (7)

This sentence should not be entailed by the in-

tended models of the PSL Ontology itself, yet

it was only identiﬁed when using the axioms of

soo

; it was a hidden consequence of the PSL

Ontology. In particular, it was the axiom below

from T

soo

that played the critical role in deriv-

ing the unintended sentence:

(∀s

, a)root(s

, a) ⊃ (∃s

) soo(s

, a)

∧ mono(s

, s

, a) ∧ same tree(s

, s

, a) (8)

As a result of this discovery, the axiom for

same tree was modiﬁed.

It is interesting to see the relationship between

this case and the failure of a potential represen-

tation theorem for the ontology. Part of the rep-

resentation theorem shows that a sentence that

is entailed by axioms is also entailed by the set

of intended models. Hidden consequences such

as we have just considered are counterexamples

to this part of the representation, since it is a

sentence that is provablefrom the axioms, yet it

is not entailed by the intended models. One can

either weaken the axioms (so that the sentence

is no longer provable), or one can strengthen

the requirements by restricting the class of in-

tended models (so that the sentence is entailed

by all intended models).

2. An examination of the proof may lead to the

detection of some error in the deﬁnition of the

requirements; in this case we must return to the

Requirements Phase. It is important to devote

considerable attention to the detection of this

possibility so that the ontology is not revised to

satisfy incorrect requirements.

We did not encounter an example of this in

our experiences, however it would be possible

for an error in the requirements speciﬁcation

to lead to an unintended proof. As discussed

above, this type of error could be addressed by

strengthening the requirements.

Case 2: No Proof Found. As a result of the semi-

decidability of ﬁrst-order logic and the inherent

intractability of automated theorem proving, if no

proof is found when testing for a particular re-

quirement then a heuristic decision regarding the

state of the lifecycle must be made. It could be the

case that no proof is found because the sentence

really is not provable; there may be a mistake in

the deﬁnition of the requirement that we are test-

ing, or there may be an error in the axiomatization

of the ontology, (i.e. we cannot prove that the re-

quirement is met because it is not met). However,

it could be the case that due to the intractability of

automated theorem provers, a proof exists but the

theorem prover is unable to ﬁnd it (at least within

some time limit). To avoid unnecessary work,

some effort must be made to ensure that we are

as informed as possible when making this deci-

sion; in particular, previously encountered errors

and the nature of the requirement that we are at-

tempting to prove is satisﬁed must be taken into

account. The heuristic decision is a choice be-

tween the following options:

1. If we believe there may be some error in the

requirements or the design of the ontology, then

we must revisit the Requirements Phase or the

Design Phase, respectively. It is recommended

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

that the Requirements Phase is revisited ﬁrst, as

generally a much smaller investment is required

to investigate the correctness of a requirement,

rather than that of the ontology.

In the course of proving the representation the-

orem for T

soo

, the theorem prover failed to

entail a property regarding the mono relation,

namely, that the mono relation should only hold

between different occurrences of the same sub-

activity. This requirement was initially ex-

pressed as the following proposition:

(∀s

, s

, o, a) mono(s

, s

, a) ∧ occurrence of(o, a)

∧ subactivity occurrence(s

, o)

⊃ ¬subactivity occurrence(s

, o) (9)

It seemed clear that the axiomatizations of the

mono relation should have restricted all satisfy-

ing models to instances where s

and s

were

not in the same activity tree. Returning to

the Requirements Phase, an examination of the

abovesentence led to the realization that the ax-

iomatization of the proposition had been incor-

rect. We had neglected to specify the condition

that s

was not the same occurrence as s

, (in

which case the subactivity occurrence relation

clearly holds for s

if it holds for s

). Once this

issue was addressed, we continued to the Ver-

iﬁcation Phase (no revisions were required to

the ontology’s design) and the theorem prover

was able to show that the ontology entailed the

corrected property, shown below.

(∀s

, s

, o, a) mono(s

, s

, a) ∧ occurrence of(o, a)

∧ subactivity occurrence(s

, o) ∧ (s

6= s

)

⊃ ¬subactivity occurrence(s

, o) (10)

The previous example was a case where the er-

ror that was corrected resulted from a misrep-

resentation of the intended semantics of the re-

quirements. Another interesting situation was

encountered where the requirements’ semantics

were redeﬁned following a series of inconclu-

sive test results. Originally, T

soo

was to be a

conservative extension of PSL

. In part, this

meant that the axiomatization of T

soo

had to ac-

count for all of the kinds of activity trees that

were represented in PSL. One particular class

of activity trees was represented by the zigzag

relation, deﬁned below.

A detailed discussion of conservative extensions and

the role that they play in ontology development can be

found in (Grau et al., 2009).

(∀s

, s

, a) zigzag(s

, s

, a) (11)

≡ (∃s

)preserve(s

, s

, a)

∧ preserve(s

, s

, a) ∧ ¬preserve(s

, s

, a)

With the inclusion of the zigzag class in T

soo

were unable to entail the transitivity of the pre-

serve relation. Review of the inconclusive test

results led to the belief that with the inclusion

of the zigzag class of activity trees:

soo

∪ T

psl

6|= (∀s

, s

, a) preserve(s

, s

, a)

∧ preserve(s

, s

, a) ⊃ preserve(s

, s

, a)

(12)

Careful consideration of the situation led to the

decision that the ability of T

soo

to entail the tran-

sitivity of the preserve relation was more im-

portant than developing it as a non-conservative

extension of PSL. This decision resulted in

a change in the axiomatization of T

soo

, how-

ever this change represented a change in the

requirements. We were no longer consider-

ing the zigzag class, because we had revised

the requirements such that T

soo

did not have to

be a conservative extension of PSL. After this

change was implemented, we were able to suc-

cessfully prove that the axioms of the ontology

entailed the transitivity of the preserve relation.

2. If we are strongly conﬁdent about the correct-

ness of both the requirements and the design of

the ontology, then we consider the possibility

that it is the intractable nature of the theorem

prover that is preventing a proof from being

found. In this case, we proceed to the Tuning

Phase and attempt to adapt the ontology so that

the theorem prover performance is improved to

a level where the requirements can be veriﬁed.

In another case, we were unsuccessful in

proving a particular property about the

min precedes and the preserve relations.

Based on the intended semantics of the two

relations, it would appear straightforward that

in any model where min precedes holds for

two occurrences, preserve must hold as well.

We attempted to verify this by proving that we

could entail the following proposition from the

ontology with the theorem prover, however the

results were inconclusive:

(∀s

, s

, a)min precedes(s

, s

, a)

⊃ preserve(s

, s

, a) (13)

Being fairly certain about the correctness of the

ontology and speciﬁcation of the property, we

moved to the Tuning Phase. In consideration of

THEOREM PROVING IN THE ONTOLOGY LIFECYCLE

the deﬁnition of the preserve relation and the

proposition we were attempting to verify, the

reﬂexivity of the preserve relation was an intu-

itively important property. Two lemmas regard-

ing the reﬂexivity of the mono relation that had

already been shown to satisfy the models of the

ontology were:

(∀s

, s

, a)min precedes(s

, s

, a)

⊃ mono(s

, s

, a) (14)

and

(∀s, o, a)subactivity occurrence(s, o) ∧ legal(s)

∧ occurrence of(o, a) ⊃ mono(s, s, a) (15)

The addition of these lemmas to the original

reasoning problem aided the theorem prover

sufﬁciently so that the property was proved and

we could continue testing the other require-

ments.

This example illustrates a phenomenon that

distinguishes theorem proving with ontologies

from more traditional theorem proving – we are

not certain that a particular sentence is actually

provable. Effectively, every theorem proving

task with an ontology is an open problem.

Case 3: All Requirements Met. If we obtain a

proof that a requirement is satisﬁed, and it is

consistent with the intended semantics of the

ontology, then we may proceed with testing the

remaining requirements. Once we obtain such

proofs for each requirement, the ontology we

have developed satisﬁes our requirements and we

can proceed to the Application Phase.

Note that the results of the Veriﬁcation Phase may

lead to revisions of either the design or the require-

ments of the ontology. The Design Phase is revis-

ited in the case that an error is detected or suspected

in the Veriﬁcation Phase. If an error in the design is

identiﬁed, it is noted that the developer must be cau-

tious and consider the entire design when making the

correction so that further errors are not created. Ad-

ditionally, when a correction is made to the design,

all previous test results should be reviewed, and any

tests (proofs) that were related to the error should be

rerun; an error in the design has the potential to posi-

tively or negatively impact the results of any tests run

prior to its identiﬁcation and correction. The Require-

ments Phase is revisited in the case that an error in the

requirements is found or suspected during the Veriﬁ-

cation Phase. It may also be revisited if revisions to

the requirements are necessary because of corrections

to the ontology that were implemented in the Design

Phase.

4.4 Tuning

The Tuning Phase focuses on the mitigation of theo-

rem prover intractability. Similar to the Design Phase,

the Tuning Phase develops a set of axioms, however

the input and the function of each phase makes the

two distinct. In contrast to the Design Phase, the in-

put of the Tuning Phase is a version of the ontology

that we believe to be correct, but have not been able to

conclusively test. Automated theorem provers some-

times have difﬁculty ﬁnding a proof, though one ex-

ists; the aim of this phase is to apply techniques to

streamline the ontology in an effort to mitigate theo-

rem prover intractability. This can be accomplished

with the development of subsets and the use of lem-

mas, discussed in further detail below.

To develop a subset requires that we remove some

of the axioms of the ontology that are not relevant (in

the axiomatization of the ontology) to the particular

reasoning problem we are considering. The idea is

that by excluding these axioms from the reasoning

problem, we can increase the efﬁciency of the theo-

rem prover, as it will not be considering axioms that

would not be used for the proof. By reducing the

number of clauses that must be considered by the the-

orem prover, there is the potential to reduce the time

required to ﬁnd a solution, if one exists. The selec-

tion of a subset could be, but is not necessarily based

on the modules of an ontology. Our work with the

PSL ontology often led to breaking up the axioms in a

module. We have currently not explored all aspects of

this technique in depth, however it appears that sub-

set selection introduces a new complication that must

be considered. When selecting a subset of the ontol-

ogy, we must ensure that all of the necessary axioms

have been included. If any related axiom is excluded,

this could allow for an inconclusive test result (we

might not prove a sentence because some of the ax-

ioms required to prove it have been excluded). At this

point, we do not provide any methodology to address

this challenge; a clear and complete understanding of

the ontology is required to be certain of what axioms

must be selected for a subset for a particular reasoning

problem.

For example, when working with the PSL ontol-

ogy, we could exclude axioms from PSL-Core that

had to do with timepoints when testing reasoning

problems that were related to the composition of ac-

tivities. This was possible because of our understand-

ing of the concepts of the ontology. The size of the

PSL ontology makes the use of subsets necessary for

most reasoning problems, however we have observed

that these subsets are often successfully reused for

other related reasoning problems. While testing the

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

ontology, we were able to use the same subset

successfully entail 14 of 16 propositions related to the

ordering of subactivity occurrences. .

We use the term lemma in its traditional, mathe-

matical sense. Their use to improve theorem prover

performance is a commonly accepted technique. In

the Tuning Phase, we can apply this technique to as-

sist in obtaining conclusive test results. Lemmas may

be used (in conjunction or independent of subsets)

to improve performance as a means of reducing the

number of steps required to obtain a proof. By adding

a lemma, we hope to provide the theorem prover with

a sentence that will be used in the proof; in this case

the number of steps required to obtain the proof is

reduced (since the theorem prover no longer needs

to prove the lemma before using it). We also spec-

ulate that the addition of such a lemma provides a

sort of guidance for the search, in the direction of

the desired proof. Lemmas should be developed in-

telligently, with some idea of how the addition of the

sentence to the ontology will assist in ﬁnding a proof.

Another point to consider is that of reusability. Some

effort should be made to design a lemma that is gen-

eral enough to be applied for other reasoning prob-

lems. In the event that we have already developed

a lemma for one reasoning problem, we should con-

sider its potential use in the Tuning Phase for a related

reasoning problem.

An example of the use of a lemma while testing

the PSL ontology is discussed in Case 2 in the previ-

ous section.

5 DISCUSSION

The description of the Veriﬁcation Phase in Sec-

tion 4.3.2 highlighted the heuristic decisions in the

methodology that result from the semidecidability

of ﬁrst-order logic, and the intractability of theorem

proving in this case. As discussed, if we do not obtain

a proof when testing a requirement, then we cannot be

certain if this is because a proof does not exist (if this

is the case, then we know that our current ontology

does not satisfy the requirement, unless it was incor-

rectly speciﬁed) or if a proof does exist but the theo-

rem prover reaches a speciﬁed time limit before it is

able to ﬁnd it (this would present us with either Case

1 or Case 2, as described above). We suspect that it

is this issue of uncertain paths resulting from Case 2

that will stimulate some criticism of our veriﬁcation

methodology and the lifecycle as it is proposed here.

We address this concern with the following remarks:

This subset can be found at http://stl.mie.utoronto.ca/

colore/process/psl-subset-519.clif.

• In two of the three possible cases that we have

identiﬁed, we can be certain of the direction we

must proceed in (the cases when a proof is found).

• In Case 2, when a proof is not found and there

is uncertainty about the cause, we can be certain

that the requirements for the ontology’s applica-

tion have not been met. Applications of the ontol-

ogy that utilize a theorem prover must be able to

answer a query (competency questions) or entail

a proposition (infer a property). In other words a

theorem prover must be able to ﬁnd a proof of the

requirements in some reasonable amount of time.

Therefore, we can say that in all cases the veriﬁ-

cation methodology is capable of testing if the re-

quirements are met; the uncertainty exists in how

to proceed in development when a requirement is

not met.

• The uncertainty of which path should be followed

when a requirement is not met may be mitigated.

If thorough documentation practices are followed

through development, we may seek out trends to

indicate the most likely source of the error. Addi-

tionally, sometimes a model building tool may be

used to test for the existence of counterexamples.

• Furthermore, we havedemonstrated the feasibility

and effectiveness of our methodology in practice

with examples of each possible case in the Veriﬁ-

cation Phase.

6 FUTURE WORK

One direction of future work that arose from the de-

velopment of the subactivity occurrence ordering ex-

tension of PSL is in the area of development envi-

ronments. Speciﬁcally, an environment capable of

capturing the development history of an ontology -

including test results, changes made to axioms and

requirements, and different versions of the ontology

developed in the Tuning Phase. This would be valu-

able not only from a documentation perspective, but

as a potential aid to heuristic decisions. A summary

of test results could indicate trends (design errors, or

lemmas required) that would assist the decision pro-

cess in the case that no proof is found. Also, if a

particular test remains inconclusiveafter considerable

effort, an environment capable of tracking test details

could allow the developer to temporarily leave the test

unresolved and return to it after additional tests have

been performed. With the necessary test history in-

formation available, the developer could easily and

efﬁciently apply any corrections, subsets, or lemmas

discovered in subsequent tests to the “problem” test.

THEOREM PROVING IN THE ONTOLOGY LIFECYCLE

An environment dedicated to this type of documen-

tation has the potential to be theorem prover indepen-

dent. This would be beneﬁcial since different theorem

provers may be more useful for different applications

or with different ontologies, so committing to one the-

orem prover restricts the potential application of the

methodology presented here.

Additional areas for future work that we have

identiﬁed are brieﬂy described below:

• Perform experiments to identify the possibility of

problem-general heuristics or techniques to re-

duce uncertainty in the heuristic decision follow-

ing a Case 2 of the Veriﬁcation Phase.

• Include maintenance considerations in the lifecy-

cle phases. Different types of maintenance activi-

ties (bug ﬁxes, changes in the ontology’s domain)

should be performed differently within the lifecy-

cle.

• Explore and expand on the presence of model gen-

eration as a tool for testing in the Veriﬁcation

Phase.

• Investigate the role of non-functional require-

ments in the ontology lifecycle. In keeping with

the analogy typically drawn between software and

ontology development, we identify the speciﬁca-

tion of intended models as the functional require-

ments of an ontology. This leaves the design and

evaluation of non-functional requirements to be

explored: how can these qualities be identiﬁed

and measured? and how can they be integrated

in the development lifecycle of ontologies?

7 CONCLUSIONS

Existing ontology development methodologies do not

provide an account of ontology evaluation that is ad-

equate for verifying ontologies with respect to their

model-theoretic properties. In this paper, we have

provided an approach to the ontology lifecycle that

focuses on support for semiautomatic veriﬁcation of

ontologies, including a methodology that takes into

account the pragmatic issues of semi-decidability in

ﬁrst-order logic. The effective use of such a method-

ology addresses the challenges posed by ontologies

that use more expressivelanguages, such as ﬁrst-order

logic.

Our presentation of the ontology lifecycle rests on

the connection between the mathematical deﬁnition

of the intended models of an ontology and the rea-

soning problems that are equivalent to the veriﬁcation

of these intended models with respect to the axiom-

atization of the ontology. It is this connection which

allows theorem provers to play a pivotal role in ontol-

ogy design, analysis, and evaluation.

Nothing in the methodology and semiautomatic

veriﬁcation presented here is speciﬁc to the PSL on-

tology, or to ﬁrst-order logic. The lifecycle accounts

for the difﬁculties of development with ﬁrst-order

logic; however, since the semiautomatic veriﬁcation

of requirements satisfaction could be beneﬁcial in any

application of ontology development, we close with

an invitation for the techniques presented here to be

applied with other ontologies.

REFERENCES

Bock, C. and Gr¨uninger, M. (2004). PSL: A semantic do-

main for ﬂow models. Software and Systems Model-

ing, 4:209–231.

Fern´andez, M., G´omez-P´erez, A., and Juristo, N. (1997).

Methontology from ontological art towards ontologi-

cal engineering. In Symposium on Ontological Engi-

neering of AAAI.

G´omez-P´erez, A., Corcho, O., and Fern´andez-Lopez,

M. (2004). Ontological Engineering : with ex-

amples from the areas of Knowledge Management,

e-Commerce and the Semantic Web. First Edition

(Advanced Information and Knowledge Processing).

Springer.

Grau, B., Parsia, B., and Sirin, E. (2009). Ontology inte-

gration using e-connections. In Modular Ontologies,

pages 293–320. Springer-Verlag, Berlin.

Gr¨uninger, M. (2003). Ontology of the process speciﬁcation

language. In Handbook of Ontologies, pages 599–618.

Springer-Verlag, Berlin.

Gr¨uninger, M. (2009a). The ontological stance for a man-

ufacturing scenario. Journal of Cases in Information

Systems, 11:1–25.

Gr¨uninger, M. (2009b). Using the PSL ontology. In Hand-

book of Ontologies, pages 419–431. Springer-Verlag,

Berlin.

Gruninger, M. and Fox, M. S. (1994). The role of compe-

tency questions in enterprise engineering. In Proceed-

ings of the IFIP WG5.7 Workshop on Benchmarking –

Theory and Practice.

Gr¨uninger, M. and Fox, M. S. (1995). Methodology for the

design and evaluation of ontologies. In International

Joint Conference on Artiﬁcial Inteligence (IJCAI95),

Workshop on Basic Ontological Issues in Knowledge

Sharing.

Pinto, H. S., Tempich, C., and Staab, S. (2003). Ontology

engineering and evolution in a distributed world using

diligent. In Handbook on Ontologies, International

Handbooks on Information Systems, pages 153–176.

Springer.

Sure, Y., Staab, S., Studer, R., and Gmbh, O. (2003). On-

to-knowledge methodology (otkm). In Handbook on

Ontologies, International Handbooks on Information

Systems, pages 117–132. Springer.

KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development

Uschold, M. and Gr¨uninger, M. (1996). Ontologies: Princi-

ples, methods and applications. Knowledge Engineer-

ing Review, 11:93–136.

Uschold, M. and King, M. (1995). Towards a methodol-

ogy for building ontologies. In In Workshop on Ba-

sic Ontological Issues in Knowledge Sharing, held in

conjunction with IJCAI-95.

APPENDIX

Axioms for Subactivity Occurrence

Orderings

Elements of the subactivity occurrence ordering are

elements of an activity tree.

(∀a, s) soo(s, a) ⊃ (16)

root(s, a) ∨ (∃s

) min precedes(s

, s, a)

The root of an activity tree is mapped to an el-

ement of the subactivity occurrence ordering by an

order homomorphism.

(∀s

, a) root(s

, a) ⊃ (17)

(∃s

)soo(s

, a)∧mono(s

, s

, a)∧same tree(s

, s

, a)

Every element of the activity tree is mapped to an

element of the subactivity occurrence ordering by an

order homomorphism.

(∀s

, s

, a) min precedes(s

, s

, a) ⊃ (18)

(∃s

)soo(s

, a)∧mono(s

, s

, a)∧same tree(s

, s

, a)

There is no order homomorphismbetween distinct

elements of the subactivity occurrence ordering.

(∀s

, s

, a) mono(s

, s

, a) ∧ soo(s

, a)

(19)

∧same tree(s

, s

, a) ⊃ (s

= s

)

The relation soo precedes is transitive.

(∀a, s

, s

) soo precedes(s

, s

, a)∧ (20)

soo precedes(s

, s

, a) ⊃ soo precedes(s

, s

, a)

The relation soo precedes orders elements in the

subactivity occurrence ordering.

(∀a, s

, s

) soo precedes(s

, s

, a) ≡ (21)

(soo(s

, a) ∧ soo(s

, a)

∧preserve(s

, s

, a) ∧ ¬preserve(s

, s

, a))

(∀s

, s

, a) preserve(s

, s

, a) ≡ (22)

(∃s

, s

) mono(s

, s

, a) ∧ mono(s

, s

, a)

∧min precedes(s

, s

, a)

∧same tree(s

, s

, a) ∧ same tree(s

, s

, a)

THEOREM PROVING IN THE ONTOLOGY LIFECYCLE