SUBGRAPH EXTRACTION AND MEMETIC ALGORITHM FOR

THE MAXIMUM CLIQUE PROBLEM

Duc-Cuong Dang and Aziz Moukrim

Universit

e de Technologie de Compi

egne

Laboratoire Heudiasyc, UMR UTC-CNRS 6599, BP 20529, 60205 Compi

egne, France

Keywords:

Maximum clique problem, Memetic algorithm, Triangulated graph, Circular-arc graph.

Abstract:

The maximum clique problem involves ﬁnding the largest set of pairwise adjacent vertices in a graph. The

problem is classic but still attracts much attention because of its hardness and its prominent applications.

Our work is based on the existence of an order on all the vertices whereby those belonging to a maximum

clique stay close enough to each other. Such an order can be identiﬁed via the extraction of a particular

subgraph from the original graph. The problem can consequently be seen as a permutation problem that

can be addressed efﬁciently with an evolutionary-like algorithm, here we use a memetic algorithm (MA).

Computational experiments conducted on DIMACS benchmark instances clearly show our MA which not

only outperforms existing genetic approaches, but also compares very well to state-of-the-art algorithms.

1 INTRODUCTION

A clique in a graph is a set of pairwise adjacent ver-

tices, that is to say an induced subgraph which is it-

self a complete graph. The Maximum Clique Prob-

lem (MCP) involves ﬁnding a clique with the greatest

cardinality. The MCP is one of the important prob-

lems of graph theory, and is computationally equiv-

alent to both the Maximum Independent Set Prob-

lem (MISP) and the Minimum Vertex Cover Prob-

lem (MVCP). The problem has been proved to be

NP-Hard (Garey and Johnson, 1979) for an arbitrary

graph. For some special graphs such as triangulated

graphs, interval graphs and circular-arc graphs, the

MCP can be solved in linear time (Golumbic, 2004).

The MCP has numerous applications in a variety of

domains including information retrieval, signal trans-

mission and bioinformatics (Balas and Yu, 1986; Ji

et al., 2004). Therefore, it is important to design ef-

ﬁcient heuristics to solve different instances in a rea-

sonable computation time.

Many heuristic approaches have been developed

for the MCP, most of which are modiﬁed version

of different local search techniques, while others are

metaheuristics (for an overview of these methods, see

(Bomze et al., 1999; Pardalos and Xue, 1994)). Re-

cent published methods have been tested using bench-

mark instances from the Second DIMACS Challenge

(Johnson and Trick, 1996), but comparing experimen-

tal results remains difﬁcult, from the point of view

of both the quality of the solutions and their com-

putation time, owing to differences in experimental

testing protocols and the large variety of machines

used. However, if we consider only the quality of

the solutions reported by authors of these methods,

two stand out as being state-of-the-art for the MCP.

First, Reactive Local Search (RLS) (Battiti and Pro-

tasi, 2001) is a tabu search with a feedback scheme to

adapt the tenure parameter and to restart the process

when required. A recent evolutionary approach ex-

tending the reactive scheme has been reviewed by the

authors

. Secondly, Variable Neighborhood Search

(VNS) (Hansen et al., 2004) is, as its name suggests,

a variable neighborhood search using the simplicial

vertex test during its descent steps. Certain other

methods, comparable to the state-of-the-art, are wor-

thy of note. K-opt Local Search (KLS) (Katayama

et al., 2005) is a quick variable-depth search tested

in a basic multi-start scheme. Ant Colony Optimiza-

tion (ACO) (Solnon and Fenet, 2006) is a recent ant

colony optimization approach for the MCP. Quick Al-

most Exact Maximum Weight Clique/Independent Set

Solver (QUALEX-MS) (Busygin, 2006) is a deter-

ministic greedy construction algorithm based on a

quadratic formulation of the MCP. Dynamic Local

Search (DLS) (Pullan and Hoos, 2006) is a stochastic

http://rtm.science.unitn.it/˜battiti/

Dang D. and Moukrim A..

SUBGRAPH EXTRACTION AND MEMETIC ALGORITHM FOR THE MAXIMUM CLIQUE PROBLEM.

DOI: 10.5220/0003081000770084

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 77-84

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

local search with dynamic penalty adjustment for ver-

tex selection. The DLS focuses on ﬁnding a clique of

given size. It was tested on different global schemes

(Pullan and Hoos, 2006; Pullan, 2006; Grosso et al.,

2008).

Genetic Algorithms (GA) have been shown to be

efﬁcient for many hard combinatorial optimization

problems, but pure genetic schemes applied for the

MCP have poor performances when compared to lo-

cal search techniques (Park and Carter, 1995). Con-

sequently, most efﬁcient GA designs for the MCP are

hybrids between a genetic scheme and a local search

(Bui and Eppley, 1995; Marchiori, 1998; Singh and

Gupta, 2006). One common feature of these GA is

that they use a binary representation of the chromo-

some.

In this paper we focus on GA designs in which

local search techniques replace the mutation proce-

dures of classic GA, and we refer to Memetic Algo-

rithms (Moscato, 1999). Moreover, we propose using

a permutation of the set of vertices as a representa-

tion, meaning that an evaluation process is then re-

quired to identify the associated clique. This iden-

tiﬁcation is performed using a subgraph extraction

approach which targets interval graphs, circular-arc

graphs and triangulated graphs. Three algorithms,

that we called VMTG (vertex-maximal extraction us-

ing triangulated graphs), EMTG (edge-maximal ex-

traction using triangulated graphs) and CAG (extrac-

tion using circular-arc graphs) are developed for this

purpose.

The paper is organized as follows. We ﬁrst

present, in Section 2, a formal description of the MCP

with a short description of our approach to solve the

problem. Different methods to evaluate a permuta-

tion of vertices using subgraph extraction are also de-

scribed in the section. The memetic algorithm is pre-

sented and discussed in Section 3. Numerical results

are provided in Section 4, and ﬁnally some conclu-

sions are drawn.

2 SUBGRAPH EXTRACTION

APPROACH

Let G = (V, E) be an arbitrary undirected graph where

V is the set of vertices and E ⊆ V ×V the set of edges.

The number of vertices in V will be denoted n, and the

number of edges in E will be denoted m. Given a sub-

set S of V , we refer to G[S] = (S,E ∩ (S × S)) as the

subgraph induced by S. A graph G = (V, E) is com-

plete if all its vertices are pairwise adjacent, meaning

that ∀x, y ∈ V, [x,y] ∈ E. A clique K is a subset of V

such that G[K] is complete. The MCP ask to ﬁnd a

clique K with the greatest cardinality.

Our approach to solving the MCP involves, ﬁrst,

considering a permutation of all the vertices in V , i.e.

a sequence which we shall denote π, and then using an

extraction procedure to identify associated solutions,

i.e. the most proﬁtable subsequences. Both the se-

quence and the identiﬁed solution can be improved

using appropriate optimization techniques.

The most intuitively straightforward extraction

method for a given sequence π is to ﬁnd the subse-

quence (π(i),...,π(i + l

)) that can form a clique and

that has the greatest length l

. Every permutation con-

taining the vertices of a maximum clique K

max

as a

subsequence yields K

max

in return. A naive algorithm

with complexity O(n

) can be used to extract such

a subsequence. More efﬁcient extraction methods in-

volve ﬁrst extracting a subgraph from the original one,

then identifying the maximum clique from the sub-

graph. The subgraph types are chosen such that the

MCP can be solved in polynomial time, or linear time

in the ideal case. For this reason, in this section we

investigate different extraction methods using interval

graphs, circular-arc graphs and triangulated graphs.

2.1 Triangulated Graph Extraction

A graph is triangulated or chordal if every one of its

cycles of four or more nodes has a chord, that is to say

an edge joining two nodes that are not consecutive in

the cycle. We are interested in triangulated graph ex-

traction, mainly because this method has already been

proposed by (Balas and Yu, 1986) (vertex-maximal

version) and by (Xue, 1994) (edge-maximal version).

Neither of these methods starts out with a predeﬁned

permutation of vertices, but both attempt to build one

dynamically while maximizing the edge or vertex cri-

teria. We have adapted their methods for our purposes

by including a predeﬁned permutation.

For a given graph G = (V,E), a permutation of its

vertices set is deﬁned as bijection π : [1..n] → V . We

set succ

G,π

(x) = {y|π

−1

(y) > π

−1

(x) and [x, y] ∈ E}

to denote the set of successors of x in π and t

G,π

(x) to

denote the ﬁrst successor (having the smallest π

−1

(y)

value). A vertex x is said to be quasi-simplicial in

π if t

G,π

(x) is connected to every other element of

succ

G,π

(x). A graph is triangulated if and only if there

exists a permutation of vertices π, such that the in-

duced subgraph G[{x} ∪ succ

G,π

(x)] is complete for

every x ∈ V . Such a permutation is called a perfect

elimination scheme (PES). A permutation π of V is

a PES of G if and only if for all x ∈ V , x is quasi-

simplicial in π (Balas and Yu, 1986).

For a given permutation π and a subset S of V , we

refer to π

: [1..|S|] → S as the permutation restricted

ICEC 2010 - International Conference on Evolutionary Computation

to S, such that π

−1

(x) < π

−1

(y) with (x,y) ∈ S × S

and x 6= y if and only if π

−1

(x) < π

−1

(y). A subgraph

= (V

) of G is said to be π-triangulated if and

only if π

is a PES of G

. In particular, when G

an edge-induced subgraph, that is to say V

= V , it is

said to be edge-maximal if and only if ∀e ∈ E \E

, the

subgraph G

= (V,E

∪ {e}) is not π-triangulated. In

the same way, when G

is a vertex-induced subgraph,

usually noted G[S], it is said to be vertex-maximal if

and only if ∀x ∈V \S, G[S∪{x}] is not π-triangulated.

Our ﬁrst triangulated subgraph extraction for a

given permutation π, noted VMTG, is as follows. A

subset S of vertices is initialized to π(n), then we

browse vertices in π from right to left. If the cur-

rent vertex x is quasi-simplicial in π

|S∪{x}

, it will be

added to S. An example of this extraction is given in

Figure 1.b. In this example, according to permutation

= (3,2,6, 7,1,5,4), S is initialized to vertex 4 from

the original graph (Figure 1.a), then vertices 5, 1, 7,

6 are progressively added to S because their ﬁrst suc-

cessors are connected to their all other successors in

1|S

during the process. Then vertex 2 is not added

to S because its ﬁrst successor in the current π

1|S

7 and it is not connected to vertex 1, the other suc-

cessor of 2. Finally, vertex 3 is added to S and we ob-

tain the π

-triangulated vertex-induced subgraph. The

largest clique is memorized for vertex 6, because its

set of successors in π

1|S

has the greatest cardinality.

Hence, for an arbitrary graph G = (V, E), the follow-

ing proposition holds.

Proposition 1. Algorithm VMTG ﬁnds a vertex-

maximal π-triangulated subgraph of G in O(n+m).

The second extraction, noted EMTG, is based on

an almost identical principle, but instead of remov-

ing the vertex we try to maximally integrate rela-

tive edges into the extracted graph while keeping the

quasi-simplicial property. An example is given in Fig-

ure 1.c. Here vertices are always added to G

at the

same time as necessary edges. With the same permu-

tation π

from previous example, the algorithm ini-

tializes G

with vertex 4 and empty edge set, then pro-

gressively adds vertex 5 and edge 5-4, vertex 1 and

edges 1-5, 1-4, vertex 7 and edges 7-5, 7-4, vertex 6

and edges 6-7, 6-5, 6-4, vertex 2 and edge 2-7 (but

not edge 2-1), vertex 3 and edge 3-2 (but not edge

3-1) to G

. The largest clique is also memorized at

adding step of vertex 6. Similarly, for an arbitrary

graph G = (V,E), the following proposition holds.

Proposition 2. Algorithm EMTG ﬁnds an edge-

maximal π-triangulated subgraph of G in O(n+m).

2.2 Interval Graph and Circular-arc

Graph Extraction

An interval graph is an intersection graph of multi-

ple segments of a line. Its generalization on a circle

(circular-arc graph) is an intersection graph of multi-

ple arcs of a circle. Intersection containing the largest

number of segments or circular-arcs is a maximum

clique of the graph, so ﬁnding the maximum clique

in these graphs can be done is linear time when all

segments or circular-arcs are well deﬁned (Golumbic,

2004). In this section, we propose extraction methods

for an arbitrary graph and a permutation of vertices

using interval graph and circular-arc graph.

Let G = (V,E) be an arbitrary graph and π be a

permutation of vertices of V . For any i in [1..n], we

denote I

= [i, i + l

] where l

is such that 0 ≤ l

≤ n − i

and ∀l ∈ [1..l

],[π(i),π(i + l)] ∈ E and X = {I

|1 ≤

i ≤ n}. The interval set X can be seen as the repre-

sentation of an interval graph G

= (V,E

). For any

couple of vertices x, y ∈ V , [x, y] ∈ E

if and only if

∩ I

0 with i = π

−1

(x) and j = π

−1

(y). Also for

any i in [1..n], we denote as J

an extension of I

which J

0 if l

< n−i or [π(i),π(1)] /∈ E. Otherwise

= [1, p

] where p

is such that 1 ≤ p

< i and ∀p ∈

[1..p

],[π(i),π(p)] ∈ E. Therefore Y = {I

∪J

|1 ≤ i ≤

n} is the representation of a circular-arc graph that

we denote

= (V,

). For any couple of vertices

x,y ∈ V , [x,y] ∈

if and only if (I

∪J

)∩(I

∪J

) 6=

with i = π

−1

(x) and j = π

−1

(y).

Proposition 3. For an arbitrary graph G = (V, E)

and a permutation π of V , we have E

⊂

⊂ E.

A direct corollary of Proposition 3 is that any

clique in G

is a clique in

and so on any clique

is also a clique in G. From now we are inter-

ested in circular-arc graph extraction instead of inter-

val graph one. The clique extraction using circular-

arc graphs, noted CAG, can be described as follows.

For each position i in the permutation, we maintain

a list L

of the vertices π( j) in which the circular-

arcs (I

∪ J

) pass through position i. Formally, L

{π

| j = [1..n] and i ∈ (I

∪ J

)}. We browse circular-

arcs all {I

∪ J

} with j ∈ [1..n] and progressively up-

date L

. At the end of this process the longest list will

correspond to the maximum clique of

. Since the

circular-arc length starting from vertex π( j) does not

exceed the degree of vertex π( j) in G, the ﬁnal com-

plexity of this process is obviously O(n + m). An ex-

ample of this subgraph extraction is shown in Figure

1.d. We consider permutation π

= (4,5, 1,7, 6,2,3),

the algorithm can start from any vertex in the order

and for simple, following this order until returning to

the same vertex. For example we begin with vertex 5,

its ﬁrst unlinked vertex in the order is vertex 2, so 5

SUBGRAPH EXTRACTION AND MEMETIC ALGORITHM FOR THE MAXIMUM CLIQUE PROBLEM

is added to L

, L

and L

. In the same way 1 is

added to L

, 7 is added to L

, L

and L

, 6 is added to

, 2 is added to L

and L

, 3 is added to L

and ﬁ-

nally 4 is added to L

, L

and L

. The longest

list is now L

contains the maximum clique (4, 5, 6,

7) of the extracted graph.

All algorithms VMTG, EMTG and CAG have the

following property.

Property 1. For an arbitrary graph G = (V, E), there

exists a permutation of V as input of the algorithm

that gives in output a maximum clique of G.

For VMTG and EMTG algorithms, it is enough

for vertices of a maximum clique to stick together in

the end of the permutation in order to ﬁnd the clique.

For CAG algorithm, it is enough for those vertices to

stick together at any position of the permutation. So

the CAG algorithm dominates the earlier mentioned

straight forward method. These permutations are suf-

ﬁcient to show the correctness of Property 1, even

though other kinds of permutation giving a maximum

clique in output exist as seen in the example of Figure

1. In the next section, we describe how to ﬁnd such a

permutation using evolutionary approaches.

3 MEMETIC ALGORITHM

One of the metaheuristics that have proved to be ef-

fective in addressing permutation problem is the ge-

netic algorithm (GA). When local search techniques

(LS) are used instead of mutation processes in clas-

sical GA, the method is termed a memetic algorithm

(MA) (Moscato, 1999). This section describes the de-

tail of our MA design.

3.1 Population Management

In GA design, the population is a set of individuals or

solutions. In our MA each individual is represented

by a permutation of vertices or by a sequence. In order

to transform a sequence into a solution or a clique, an

evaluation process is required. We make this evalua-

tion process correspond to calling an eval() function,

using one of the three methods described in Section

2. For convenience we consider all permutations in

circular order. VMTG and EMTG algorithms in par-

ticular require a linear order to operate, so the circular

order can be transformed into linear one starting from

a speciﬁc open point. The position of this open point

is initialized to random for new created permutations,

i.e at initialization or through the crossover operator,

but for improved permutations from local search pro-

cess the value is especially given (see Section 3.2).

This value has no signiﬁcation for CAG algorithm.

We now discuss how to evolve these individuals to-

ward better ones.

The population is sorted hierarchically, ﬁrst by

identiﬁed clique size and then by generation num-

ber. A new individual created via crossover and mu-

tation operations is a candidate for insertion into the

population. This insertion requires the new individ-

ual to have a performance at least equal to that of

the worst individual, and sufﬁciently different from

the two closest individuals in the population hierar-

chy, for example with at least 5 distinct vertices. To

distinguish two individuals, we use the Hamming dis-

tance on extracted cliques. A successful insertion is

followed by the ejection of the last individual in the

hierarchy, so as to maintain the existing population

size.

3.2 Crossover Operator and Local

Search as Mutation

At each iteration of the algorithm two parents are se-

lected via a binary tournament for crossover opera-

tion. Our crossover operator, called MOX, works with

a heritage mask, a binary string of size n. The child

sequence will inherit from one parent all the vertices

in the mask having the value 1, and from the other par-

ent the remaining vertices, in the same order. There

are different ways to generate an efﬁcient heritage

mask, the most simple is to put randomly values 0

and 1 with equal probability. Then, from a random

position in the mask, we create a subsequence of

max

size with values 1 (|P

max

| is the best known clique size

of two parents). The idea is to break and merge ran-

domly different cliques from the permutations.

After a child sequence is created using MOX and

evaluated, it will have pm probability of being mu-

tated through local search (LS). During this process,

three neighborhoods are applied in stochastic order

until no further improvement can be found. Here

we denote as K the current clique, as N

|K|

the set of

vertices that connect to all the vertices in K, and as

|K|−1

(x) (with x ∈ K) the set of vertices that connect

to all vertices in K except x. The number in parenthe-

ses is the stochastic priority ps of the neighborhood,

that means the neighborhood has probability

∑

be selected.

• k-opt inner loop (5), the inner loop of the heuristic

k-opt (Katayama et al., 2005), for each iteration,

remove one vertex in K having greatest value of

|K|−1

(x)| then try to complete the clique with

vertices having the greatest degree in the induced

subgraph G[N

|K|

]. Removed and added vertices

ICEC 2010 - International Conference on Evolutionary Computation

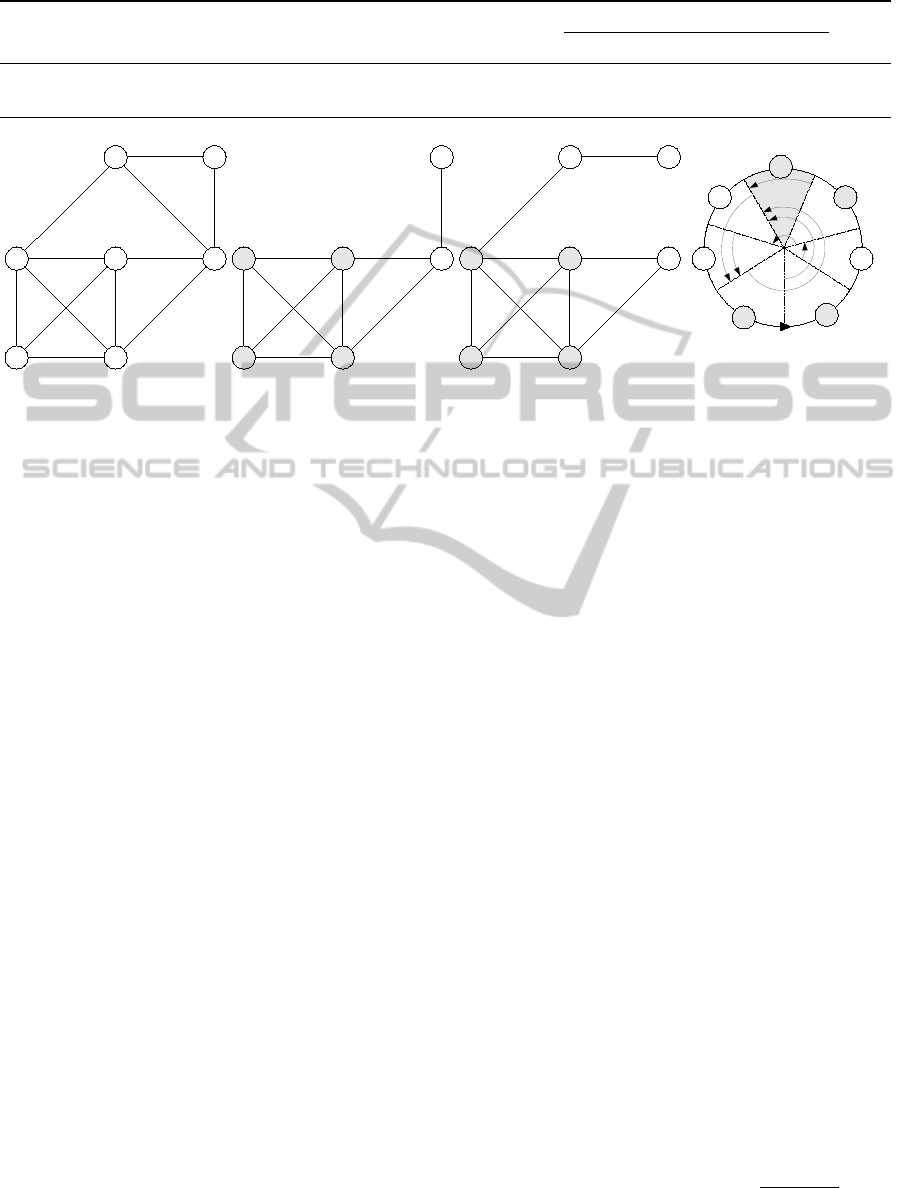
Table 1: Overall performance comparison on DIMACS benchmark.

Method RLS HSSGA GA VNS KLS PLS

Best

VMTG EMTG CAG

∑

2849 2832 2819 2851 2845 2856 2854 2859 2855 2862

∑

CPU 6715.08 4774.65 926.8 6453.48 148.24 1017.5 4332.88 11264.46 4062.25

a) an example of graph

d) extracted circular-arcs

for sequence π

b) vertex-maximal

-triangulated subgraph

c) edge-maximal

-triangulated subgraph

4 1

Figure 1: Examples of subgraph extraction with π

= (3,2,6,7,1,5,4) and π

= (4,5,1,7,6,2,3). In this particular example,

is reversed order of π

and algorithm CAG (d) gives the same graph as EMTG (c) in return.

are marked to avoid using in next iterations. The

loop is stopped when the current clique does not

contain any vertex from the original one. The

highest score is maintained during the process. At

the end of the loop, it is compared with the origi-

nal clique in order to detect an improvement.

• heuristic drop/add (3), for each iteration, remove

d vertices with priority to vertices having the

greatest value of |N

|K|−1

(x)| from the original

clique, then complete it with vertices having the

greatest degree in the induced subgraph G[N

|K|

The value of d is initialized to 1 and duplicated

after each iteration. The loop is stopped when

an improvement is found or when d is gone over

|K|− 1.

• random drop/add (2), similar to heuristic

drop/add except vertices are randomly selected

during dropping and adding step.

After the local search, to convert the improved

clique back into a sequence, vertices from the clique

are ﬁrst placed in an empty sequence at a random

starting position. The sequence is then randomly

completed with the other vertices in the remaining

position. The open point for transforming a circular

order to linear order is set to the ending position of

placed clique.

4 NUMERICAL RESULTS

The DIMACS instance set for the MCP and Graph

Coloring Problem (GCP) was released in 1993 for the

DIMACS series of challenges in combinatorial opti-

mization. Since that time it has been used as a bench-

mark to evaluate the efﬁciency of heuristics developed

for the MCP. We therefore tested our algorithm on this

set in order to compare its performance with other

methods in the literature. The set consists of 80 in-

stances, generation methods being described in (John-

son and Trick, 1996). Most recent published heuris-

tics focus on 37 instances only, rather than on the full

set. These focused instances range in size from 125

vertices and 6000 edges to 4000 vertices and 5000000

edges.

Following a large number of experiments on DI-

MACS instances, we decided to set the parameters of

our algorithm as follows: the population size is ﬁxed

at 40 individuals, and it is unnecessary to include

some good individuals when initializing the popula-

tion, i.e. by using a heuristic rather than a random gen-

eration. We denote as iter

ine f f ective

the current num-

ber of consecutive iterations without improvement.

The algorithm is stopped after iter

ine f f ective

reaches a

value iter

max

. For small instances (less than 1000 ver-

tices) we set iter

max

to 20.n, and for larger instances

we set iter

max

to n. Every individual created though

crossover has a probability pm = 1−

iter

ine f f ective

iter

max

of be-

ing mutated. All results for each instance are reported

SUBGRAPH EXTRACTION AND MEMETIC ALGORITHM FOR THE MAXIMUM CLIQUE PROBLEM

after 100 executions. Our experiments were run on

an Intel Core 2 Duo E6750 - 2.67 GHz personal com-

puter with 2 GB RAM, using a single-threaded pro-

gram. Computer performance, reported by Sandra

SiSoft

, in single core mode is 9280 MFLOPS and

10770 MIPS. The DIMACS Machine Benchmark

re-

quired respectively 0.02, 0.23, 1.40 and 5.36 CPU

seconds for solving r200.5, r300.5, r400.5 and r500.5

sample instances.

Table 2 reports our detailed results for DIMACS

benchmarks. The column |K| indicates clique size

found in solution over executions, here |K|

worst

|K|

best

and the standard deviation are reported. The

column CPU indicates average CPU time per exe-

cution with standard deviation. Finally the column

N reports the number of executions where |K|

best

reached. Over these results, it should be observed

EMTG extraction gives the best performance for MA

but it requires extended execution time. This is likely

due to additional memory usages for saving edge

structures of the extracted subgraph during evalua-

tion process. VMTG and CAG extractions give quite

similar performance but CAG runs slightly faster than

VMTG as it has very simple implementation.

Our overall results on 37 DIMACS instances, us-

ing different extractions VMTG, EMTG and CAG,

are compared to those obtained by genetic algorithms

reported by (Marchiori, 1998) (GA) and by (Singh

and Gupta, 2006) (HSSGA), and to the state-of-the-

art reported by (Battiti and Protasi, 2001) (RLS) and

by (Hansen et al., 2004) (VNS). We also compare our

results to those reported by (Katayama et al., 2005)

(KLS) and by (Pullan, 2006) (PLS). Table 1 reports

for each method the overall performance with respect

to the total number of vertices in identiﬁed cliques,

denoted

∑

and the average CPU time for execut-

ing full DIMACS set, denoted

∑

CPU . For our MA,

CPU time for each execution is full running time of

the algorithm. For other methods, the authors re-

ported this value only as time from starting of the al-

gorithm until the discovery of the best solution. Re-

sults from other excellent methods, sometimes out-

performing state-of-the-art methods, are not shown

in Table 1, either because certain results were lack-

ing or because different testing protocols were used.

Regarding these methods, we remarked the follow-

ing: ACO by (Solnon and Fenet, 2006) has an over-

all score of 1756 without reporting the result for the

MAN a81 instance; DLS by (Pullan and Hoos, 2006)

has excellent overall score of 2856 with parameters

customized for each instance (as early development of

PLS); ILS by (Grosso et al., 2008) did not report some

http://www.sisoftware.net/

ftp://dimacs.rutgers.edu/pub/dsj/clique/

results, but the algorithm obtained a record clique size

for the C2000.9 instance (80 vertices instead of the 78

in the literature).

These results clearly demonstrate that our

Memetic Algorithm compares very well with

the other genetic algorithms. MA outperforms

the GA proposed by (Marchiori, 1998) and the

HSSGA proposed by (Singh and Gupta, 2006)

in terms of efﬁciency, and it is also competitive

with state-of-the-art algorithms. Other details of

our results including experiments on BHOSLIB

(Benchmarks with Hidden Optimum Solutions

for Graph Problems) instances are available at

http://www.hds.utc.fr/∼dangducc/mclique/.

5 CONCLUSIONS AND FUTURE

WORK

We have proposed a memetic algorithm for the MCP

which not only outperforms other genetic approaches,

but is competitive with state-of-the-art approaches.

For the ﬁrst time the order of the vertices has been

used to represent a chromosome in the genetic ap-

proach for solving the MCP. Finally, it is sure that

the MA can be more engineered to improve stability,

efﬁciency and execution time but the current results

have been shown the subgraph extraction approach

and memetic algorithms are promising research direc-

tions for solving the MCP and related combinatorial

problems.

Given that a large number of fast and effective

local searches have been developed for the MCP, as

future work we plan to investigate the performances

of some of these inside the memetic scheme. More-

over, since the subgraph extraction approach is not re-

stricted to using genetic algorithms as a global search

method, we also intend to test other schemes.

REFERENCES

Balas, E. and Yu, C. (1986). Finding a maximum clique

in an arbitary graph. SIAM Journal of Computing,

15:1054–1068.

Battiti, R. and Protasi, M. (2001). Reactive local search for

the maximum clique problem. Algorithmica, 29:610–

637.

Bomze, I., Budinich, M., Pardalos, P., and Pelillo, M.

(1999). Handbook of Combinatorial Optimization,

chapter The maximum clique problem. Kluwer Aca-

demic Publishers.

Bui, T. N. and Eppley, P. H. (1995). A hybrid genetic algo-

rithm for the maximum clique problem. In Proceed-

ICEC 2010 - International Conference on Evolutionary Computation

ings of the 6th International Conference on Genetic

Algorithms, pages 478–484.

Busygin, S. (2006). A new trust region technique for the

maximum weight clique problem. Discrete Applied

Mathematics, 154:2080–2096.

Garey, M. R. and Johnson, D. S. (1979). Computers

and Intractability: A guide to the Theory of NP-

Completeness. Freeman, San Francisco, CA, USA.

Golumbic, M. C. (2004). Algorithmic Graph Theory and

Perfect Graphs (Annals of Discrete Mathematics, Vol

57). North-Holland Publishing Co.

Grosso, A., Locatelli, M., and Pullan, W. (2008). Sim-

ple ingredients leading to very efﬁcient heuristics for

the maximum clique problem. Journal of Heuristics,

14(6):587–612.

Hansen, P., Mladenovic, N., and Urosevic, D. (2004). Vari-

able neighborhood search for the maximum clique.

Discrete Applied Mathematics, 145:117–125.

Ji, Y., Xu, X., and Stormo, G. D. (2004). A graph theori-

cal approach for predicting common RNA secondary

structure motifs including psudoknots in unaligned se-

quences. Bioinformatics, 20:1591–1602.

Johnson, D. and Trick, M. (1996). Cliques, Cloroing And

Satisﬁability: Second DIMACS Implementation Chal-

lenge, volume 26 of DIMACS Series. American Math-

ematical Society.

Katayama, K., Hamamot, A., and Narihisa, H. (2005).

Solving the maximum clique problem by k-opt local

search. Information Processing Letters, 95:503–511.

Marchiori, E. (1998). A simple heuristic based genetic al-

gorithm for the maximum clique problem. In ACM

Symposium on Applied Computing, pages 366–373.

Moscato, P. (1999). New Ideas in Optimization, chap-

ter Memetic Algorithms: a short introduction, pages

219–234. McGraw-Hill Ltd., UK.

Pardalos, P. and Xue, J. (1994). The maximum clique prob-

lem. Journal of Global Optimization, 4:301–328.

Park, K. and Carter, B. (1995). On the effectiveness of ge-

netic search in combinatorial optimization. In Pro-

ceedings of the 10th ACM Symposium on Applied

Computing, pages 329–336.

Pullan, W. (2006). Phased local search for the maximum

clique problem. Journal of Combinatorial Optimiza-

tion, 12:303–323.

Pullan, W. and Hoos, H. H. (2006). Dynamic local search

for the maximum clique problem. Journal of Artiﬁcial

Intelligence Research, 25:159–185.

Singh, A. and Gupta, A. K. (2006). A hybrid heuristic for

the maximum clique problem. Journal of Heuristics,

12:5–22.

Solnon, C. and Fenet, S. (2006). A study of ACO capabili-

ties for solving the maximum clique problem. Journal

of Heuristics, 12.

Xue, J. (1994). Edge-maximal triangulated subgraphs and

heuristics for the maximum clique problem. Network,

24:109–120.

SUBGRAPH EXTRACTION AND MEMETIC ALGORITHM FOR THE MAXIMUM CLIQUE PROBLEM

Table 2: Detailed results on DIMACS benchmark (* if optimality is proved).

No. Instance Best

VMTG EMTG CAG

|K| CP U N |K| CP U N |K| CP U N

1 C125.9 34* 34 1.82(0.03) 100 34 2.09(0.03) 100 34 1.86(0.03) 100

2 C250.9 44* 44 8.97(0.12) 100 44 11.62(0.12) 100 44 8.18(0.11) 100

3 C500.9 57 57 53.77(2.47) 100 57 88.9(6.4) 100 57 43.59(3.66) 100

4 C1000.9 68 65-68(0.74) 24.16(6.69) 1 65-68(0.59) 57.71(11.96) 10 66-68(0.54) 22.27(5.49) 12

5 C2000.9 80 74-77(0.78) 183.76(50.46) 2 75-78(0.83) 560.02(119.21) 3 75-78(0.7) 160.58(35.38) 1

6 DSJC500.5 14* 13 33.43(0.33) 100 13 61.61(0.46) 100 13 30.13(0.35) 100

7 DSJC1000.5 15* 14-15(0.5) 16.06(3.9) 56 14-15(0.45) 32.84(6.08) 28 14-15(0.5) 13.16(2.9) 45

8 C2000.5 16 15-16(0.46) 87.58(18.69) 69 15-16(0.47) 292.76(56.52) 66 15-16(0.45) 78.19(17.65) 71

9 C4000.5 18 16-18(0.22) 595.99(101.41) 3 16-18(0.22) 2328.3(373.51) 2 16-18(0.26) 506.17(83.25) 5

10 MANN a27 126* 126 26.4(0.24) 100 126 50.84(0.35) 100 126 38.26(0.32) 100

11 MANN a45 345* 344-345(0.2) 33.26(4.97) 4 344-345(0.17) 77.11(10.48) 3 344-345(0.14) 44.35(5.2) 2

12 MANN a81 1100 1098-1099(0.36) 973.2(166.16) 15 1098-1100(0.35) 2877.36(333.02) 1 1098-1099(0.31) 1282.74(240.67) 11

13 brock200 2 12* 11-12(0.2) 3.6(0.63) 96 11-12(0.31) 5.66(1.11) 89 11-12(0.37) 3.74(0.76) 84

14 brock200 4 17* 16-17(0.41) 3.94(0.84) 79 16-17(0.5) 5.71(1.36) 48 16-17(0.49) 3.43(0.72) 43

15 brock400 2 29* 25-29(1.6) 27.58(5.45) 20 25-29(0.78) 41.51(5.17) 4 25-29(1.2) 21.68(2.51) 10

16 brock400 4 33* 25-33(3.01) 31.5(6.73) 83 25-33(3.82) 44.87(8.73) 35 25-33(3.84) 24.42(6.29) 36

17 brock800 2 24* 21 177.49(7.03) 100 21-24(0.3) 354.63(29.76) 1 21 149.49(11.25) 100

18 brock800 4 26* 21-26(0.5) 189.52(22.01) 1 21-26(0.5) 386.58(55) 1 21-26(0.7) 162.54(21.58) 2

19 gen200 p0.9 44 44* 44 5.31(0.07) 100 44 6.4(0.09) 100 44 5.01(0.08) 100

20 gen200 p0.9 55 55* 55 5.33(0.07) 100 55 6.59(0.08) 100 55 5.2(0.08) 100

21 gen400 p0.9 55 55* 55 36(5.95) 100 53-55(0.84) 55.24(11.89) 77 53-55(0.94) 30.3(6.89) 67

22 gen400

p0.9 65 65* 65 29.87(0.23) 100 65 48.42(0.4) 100 65 28.03(0.32) 100

23 gen400 p0.9 75 75* 75 31(0.31) 100 75 47.97(0.8) 100 75 27.66(0.92) 100

24 hamming8-4 16* 16 5.09(0.05) 100 16 8.32(0.08) 100 16 5.15(0.05) 100

25 hamming10-4 40* 40 19.94(0.54) 100 40 45.81(0.82) 100 40 16.59(0.44) 100

26 keller4 11* 11 2(0.03) 100 11 2.84(0.03) 100 11 2.11(0.03) 100

27 keller5 27* 27 166.38(1.27) 100 27 323.29(1.39) 100 27 131.24(0.75) 100

28 keller6 59 56-59(1.06) 892.84(244.5) 28 56-59(0.58) 2348.99(441.94) 92 57-59(0.78) 658.66(144.47) 81

29 p hat300-1 8* 8 6.13(0.1) 100 8 8.59(0.08) 100 8 5.91(0.05) 100

30 p hat300-2 25* 25 15.04(0.18) 100 25 16.67(0.14) 100 25 12.36(0.1) 100

31 p hat300-3 36* 36 16.48(0.16) 100 36 19.73(0.17) 100 36 13.73(0.14) 100

32 p hat700-1 11* 11 70.56(0.83) 100 11 133.16(1.7) 100 11 64.73(0.67) 100

33 p hat700-2 44* 44 215.34(1.62) 100 44 273.2(1.66) 100 44 174.63(1.3) 100

34 p hat700-3 62 62 152.39(0.98) 100 62 255.74(1.18) 100 62 123.5(0.82) 100

35 p hat1500-1 12* 11-12(0.41) 34.66(8.14) 22 11-12(0.24) 74.9(7.21) 6 11-12(0.27) 26.83(4.25) 8

36 p hat1500-2 65 65 82.21(1.5) 100 65 151.2(2.2) 100 65 76.85(1.65) 100

37 p hat1500-3 94 94 74.29(1.73) 100 94 157.28(2.67) 100 94 58.97(1.29) 100

Total 2862 2854 4332.88 2859 11264.46 2855 4062.25

ICEC 2010 - International Conference on Evolutionary Computation