A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM

MOVEMENTS BASED ON PHYSIOLOGICAL INTER-JOINT

COUPLINGS

Till Bockemühl

and Volker Dürr

1,2

Dept. of Biological Cybernetics,

Cognitive Interaction Technology - Center of Excellence, CITEC

University of Bielefeld, PO Box 100131, 33501 Bielefeld, Germany

Keywords: Motor control, Motor synergies.

Abstract: Substantial evidence suggests that nervous systems simplify motor control of complex body geometries by

use of higher level functional units, so called motor primitives or synergies. Although simpler, such high

level functional units still require an adequate controller. In a previous study, we found that kinematic inter-

joint couplings allow the extraction of simple movement synergies during unconstrained 3D catching

movements of the human arm and shoulder girdle. Here, we show that there is a bijective mapping between

movement synergy space and 3D Cartesian hand coordinates within the arm’s physiological working range.

Based on this mapping, we propose a minimal control schema for a 10-DoF arm and shoulder girdle. All

key elements of this schema are implemented as artificial neural networks (ANNs). For the central

controller, we evaluate two different ANN architectures: a feed-forward network and a recurrent Elman

network. We show that this control schema is capable of controlling goal-directed movements of a 10-DoF

arm with as few as five hidden units. Both controller variants are sufficient for the task. However, end-point

stability is better in the feed-forward controller.

1 INTRODUCTION

The complex biomechanics of limbs like the primate

arm facilitates the generation of a remarkable variety

of dexterous and context-dependent behaviors.

However, the large number of degrees of freedom

(DoFs), e.g. ten DoFs of the human arm and

shoulder girdle, complicates the required neural

control. This issue is known as motor redundancy

problem (Bernstein, 1967).

Central nervous systems (CNS) seem to easily

overcome this problem. One proposed mechanism

used by the CNS for the solution of the redundancy

problem is the combination of several DoFs into a

small set of higher level functional control units,

typically referred to as movement synergies or

primitives. There is substantial evidence that this

general concept is realized in vertebrate nervous

systems in one way or another (for reviews see Flash

and Hochner, 2005, and Ting and McKay, 2007).

Because the complexity of the control problem

depends on the number of controlled variables, these

synergies can simplify the control of the limb. Here,

we propose and evaluate a synergy-based and

closed-loop control schema that can be implemented

as a modular artificial neural network.

Classical studies on human reaching movements

tended to search for global optimization parameters

like speed (Atkeson and Hollerbach, 1985), jerk

(Flash and Hogan, 1985), or torque change (Uno, et

al., 1989). Most, if not all of these studies were

based on well-controlled but strongly constrained

movement paradigms, such as center-out tasks with

planar movements and fixed shoulder position.

Although these studies identified movement

invariants, they did not specify models of how the

brain could use them to overcome the problem of

redundancy. Furthermore, these invariants are based

on predictive strategies, i.e. global parameters that

are optimized offline and prior to the actual

movement. In these strategies sensory feedback

during an ongoing movement plays only a minor

role.

In contrast, current concepts of goal-directed

behavior favor prospective strategies that (a)

explicitly take into account sensory feedback during

ongoing behavior and (b) define motor goals in a

task space that is then mapped to motor output

(Todorov, 2004). Both of these aspects are realized

220

Bockemühl T. and Dürr V..

A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM MOVEMENTS BASED ON PHYSIOLOGICAL INTER-JOINT COUPLINGS.

DOI: 10.5220/0003084102200226

In Proceedings of the International Conference on Fuzzy Computation and 2nd International Conference on Neural Computation (ICNC-2010), pages

220-226

ISBN: 978-989-8425-32-4

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

in the approach we propose here: (a) It relies on

continuous sensory feedback and (b) exploits a small

set of movement synergies, which can be viewed as

a set of elementary motor tasks as each synergy by

itself defines a valid movement.

In a previous experiment (Bockemühl, et al.,

2010) we studied natural and unconstrained arm

movements during a catching task in a large portion

of the arm’s workspace and recorded 10-D joint

angular time courses thereof. Using principal

components analysis (PCA) for synergy extraction

we found that the distribution of recorded postures

that occur during movements can be described

efficiently by linear combinations of a set of three

inter-joint couplings. We also found that the

individual contributions of these kinematic synergies

varied systematically with catching position in

external (Cartesian) hand coordinates. Together with

the fact that three is the minimum number of

synergies for control of end-effector position in 3D,

this suggests that neural control of arm movements

may exploit a simple mapping between synergy

space and Cartesian space. Here, we show that the

mapping between synergy space and hand position is

bijective within a large physiological working range.

Based on the three movement synergies that

capture natural inter-joint couplings, we propose a

simple closed-loop control schema for a 10-DoF

limb consisting of shoulder girdle, upper and lower

arm and hand. All elements of this schema are

implemented as ANNs. We evaluate two alternative

ANN variants as central controller: a multilayer

feed-forward network and a recurrent Elman

network.

We show that both controller variants we

examine here can generate physiological trajectories

of goal-directed reaching movements, similar to

those found experimentally. The networks are also

capable of generating reaching movements towards

novel targets, as well as smoothly interpolating

between two different movements. Internal

recurrence in the Elman controller improves learning

of physiological training data. In contrast to the

multilayer feed-forward network, however, the

Elman controller shows a tendency to drift and fails

to maintain a resting posture that keeps the hand at

the target position.

2 MATERIAL AND METHODS

2.1 Kinematic Model

We use a 10 DoF kinematic model of the human

upper limb, i.e., arm and shoulder girdle. The model

comprises 4 segments corresponding to a collarbone

that moves the shoulder joint with 3 DoFs, a

shoulder joint that moves the upper arm with 3

DoFs, an elbow and lower arm with 2 DoFs, and a

hand with 2 DoFs. Segment lengths within the

model are adjusted individually for each one of nine

recorded human subjects (Bockemühl, et al., 2010).

Consequently, each set of 10 joint angles is

equivalent to a unique posture, and standard forward

kinematics can be used to calculate the hand position

(end-effector).

2.2 Inter-joint Coupling Gives Rise to

Movement Synergies

The inter-joint couplings found in natural human,

one-handed catching movements are equivalent to

the first three principal components (PCs) of 10-D

arm postures (Bockemühl, et al., 2010). Each PC

constitutes a movement synergy so that each posture

can be described by a linear combination of the

mean posture of the original data set and a weighted

sum of three movement synergies. Because the

kinematic model, mean posture, and movement

synergies are fixed for a given subject, any hand

position in 3-D Cartesian space can solely be

described by a 3-D vector of scores that scale the

contribution of each synergy (see Equation 1).







)()(

tst vmp

(1)

Here, p(t) represents a 10-D posture at time t, m

is the mean posture, s

(t) is the score of the posture

p(t) on the i

synergy, and v

is the i

synergy.

Modulating the scores in a target-dependent manner

therefore generates target-dependent hand

trajectories.

2.3 Control Structure and Artificial

Neural Networks

Given the current hand position and a target

position, e.g., the position of a ball to be caught, our

main goal is to generate an appropriate time series of

postures that moves the hand from its current

position to the target. Appropriate means that hand

trajectories should match the measured ones. Since

natural movements are marked by substantial inter-

joint couplings, we propose a control structure that

exploits these natural inter-joint couplings (Fig. 1).

This control schema contains an ANN module

that implements motor synergies in the form of a

A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM MOVEMENTS BASED ON PHYSIOLOGICAL

INTER-JOINT COUPLINGS

221

feed-forward network (called synergy network in

Fig. 1). This module maps 3-D score vectors onto

10-D posture vectors in analogy to Equation 1.

The output of the synergy network can be

described by







ijijj

swmp

(2)

where w

is the weight matrix which is equivalent to

the 3x10 loadings of the PCs and that are used as

motor synergies here. The controller compares the

target position vector with the current hand position

and calculates the score changes necessary to

minimize the difference. The result is added to the

current 3D score vector, thus updating the arm

posture for the next iteration.

We evaluate two different ANN controller

variants. The first is a two-layered feed-forward

network; the second is a recurrent Elman network

(Elman, 1990). Both ANNs are identical except for

the additional recurrent connections comprising the

context layer of the Elman network (Figure 1).

Owing to the small number of synergies, input

and output of the controller are minimal and

equidimensional: both the two input position vectors

and the output synergy scores are three-dimensional.

The output Δs of the two-layered feed-forward

network can be calculated by

,1 ,

out out in in

wwwwx

ji i

kkn kj







  







(3)

Output of the recurrent Elman network can be

calculated by the Equations 4 and 5. First, the

intermediate output y

hidden

at time t has to be

determined by

() () ( 1)

hidden in in cont hidden

ji i

hjhh

ytw wxtwyt











  



(4)

Then, the output Δs at time t can be calculated

according to









hidden

hhk

out

nkk

tywwts

,1,

)()(

(5)

The input vector x in Eq. 3 and 4 contains the

coordinates of the target position, tp, and the current

hand position, cp (see Fig. 1). σ(x) is a hyperbolic

tangent function used as sigmoid activation function

of the hidden layer.

Figure 1: Control schema with inserts showing the synergy

network (top insert) and two ANN controller variants

(bottom insert). Black structures only: two-layer feed-

forward network. Black and gray structures combined:

recurrent Elman network. For clarity, the number of

hidden units is set to 3 (h

to h

ICFC 2010 - International Conference on Fuzzy Computation

222

2.4 Network Training

Training data consist of a series of eight goal-

directed hand trajectories recorded during

experiments in which participants were instructed to

catch an approaching ball (Bockemühl, et al., 2010).

Each trajectory starts at one of two initial positions,

ends at one of sixteen target positions, and contains

25 time steps. Half of the data set (eight trajectories)

is used for training, the other half is used for testing

generalization (further eight trajectories). In order to

account for end-point stability, each trajectory is

extended by a leading initial phase of 5 time steps

during which the hand remains at the initial position,

and a trailing target phase of 10 time steps during

which the hand remains at the catching position. In

accordance, the target position tp is kept at the

initial position for 5 time steps and is subsequently

set to one of the 16 prospective catching positions

for the remaining trial.

The goal of the training is to find weight

matrices for the controller ANNs that generate

physiologically plausible hand trajectories towards

the target. The root mean squared error (RMSE)

between training trajectories and generated

trajectories was used as the evaluation function.

Weight matrix optimization was realized via the

Levenberg-Marquardt algorithm (Levenberg, 1944,

Marquardt, 1963) implemented in MatLab 7.10 (The

Mathworks). To avoid local minima, the training

was repeated 100 times, using different randomly

initialized weight matrices. As a main objective of

this study was to determine the minimal size of the

hidden layer, we tested ANNs with 3, 4, 5, 6 or 10

hidden units.

3 RESULTS

3.1 The Mapping between Synergy

Space and Cartesian Space is

Bijective

As our movement synergies are principal

components of the joint angle space, they describe

correlations between joint angles. Owing to the

PCA, these synergies are orthogonal to each other.

However, the mapping of synergy space into

Cartesian space involves non-linear forward

kinematics of the controlled arm and, therefore,

needs not be bijective: multiple postures, and

therefore synergy combinations, could result in the

same hand position. A bijective mapping is a

prerequisite for simple control of arbitrary point-to-

point movements though. To ensure that the

mapping allows arbitrary hand positioning within its

working range (surjective mapping) and that any

combination of synergies leads to distinct hand

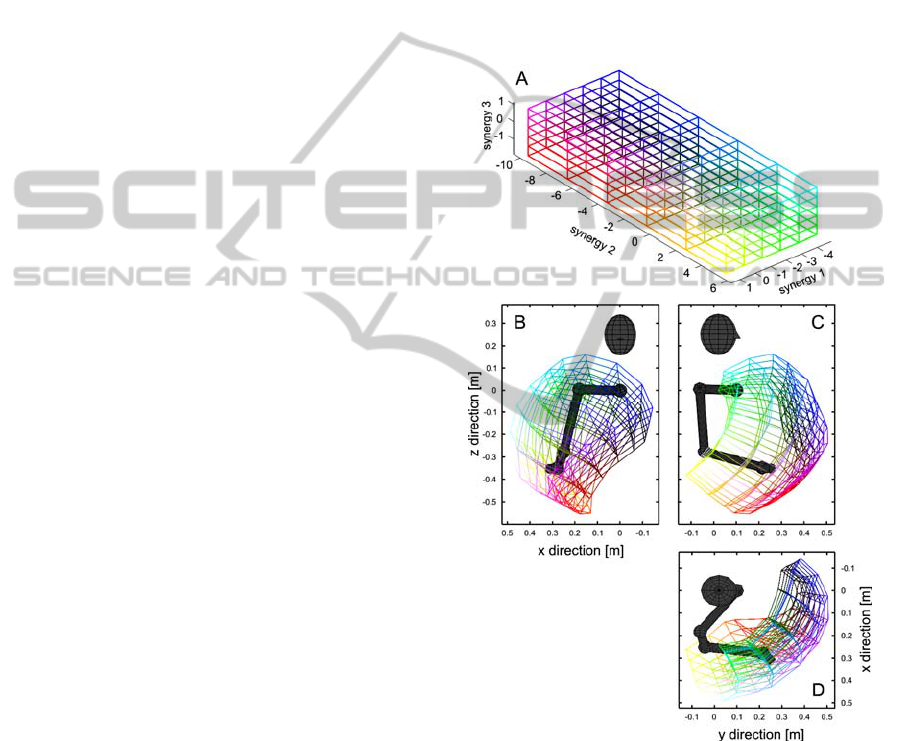
positions (injective mapping), Fig. 2 shows the

mapping of a 3D grid of synergy combinations into

Cartesian space of hand positions. Although the

mapping is non-linear, it covers a substantial

fraction of the physiological range of a human arm

(surjective) and the warped grid in Cartesian space

has no overlapping regions (injective).

Figure 2: Mapping between synergy space (A) and

Cartesian space (B, C and D) of the right human arm. B:

Frontal view. C: View from the right. D: Top view. The

kinematic model as well as a stylized head are depicted in

gray. Colors in synergy space correspond to the equivalent

color in Cartesian hand space and vice versa.

3.2 Training and Generalization

Performance

We find that both controller variants are able to

adapt to the training data. Figure 3 shows

A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM MOVEMENTS BASED ON PHYSIOLOGICAL

INTER-JOINT COUPLINGS

223

representative results for training and generalization

performance, using data from a single subject and

initial position.

During training, the networks with more than

four hidden neurons reached RMSE values of less

than 20 mm, regardless of network type. Elman

networks with six or more hidden units even reached

values as low as 5 mm. However, generalization

performance leveled off at hidden layer sizes above

4 units. As generalization is as important as learning

performance on trained data, we used 5 hidden units

for both controller variants in all other experiments.

Figure 3: Performance of networks during training and

during generalization. A: performance of feed-forward

networks. B: performance of recurrent Elman network.

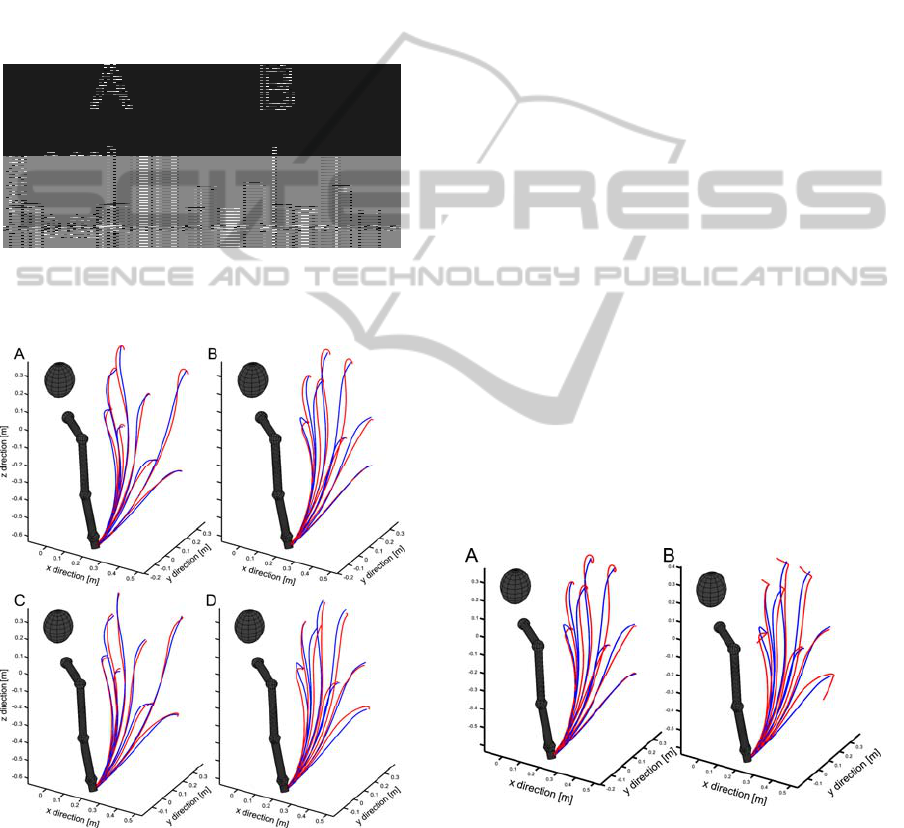
Figure 4: Representative trajectories during 40 time steps

generated by a feed-forward network (A and B) and an

Elman network (C and D) containing five hidden units. A

and C: trajectories to target positions encountered during

training. B and D: trajectories to novel target positions.

Red: trajectories generated by networks. Blue: trajectories

measured during experiment. At the same time, blue

trajectories seen in A and C are the training trajectories.

View from the rear right side of the kinematic model.

To illustrate overall controller performance,

Figure 4 shows representative trajectories produced

by a feed-forward network and an Elman network.

Whereas trajectories of both controller variants are

similar during the first half of the corresponding

movements, differences occur toward the end of the

trajectory. Here, the feed-forward network produces

a small, terminal curvature in the vicinity of the

target position. In comparison, the terminal

trajectory of the Elman network shows less deviation

from the physiological reference data, except for a

small but distinct kink near the end.

3.3 End-point Stability

An important aspect of target-directed movement is

the ability to keep the end-effector at the target after

reaching it. We tested this ability of both controller

variants by extending the presentation of target

inputs by 70 time steps. A representative result is

depicted in Figure 5. The prolonged holding phase

emphasizes the differences in end-point stability.

The feed-forward controller is much better in

keeping the end-effector at the target, though the

spirals at the end of high trajectories indicate

damped oscillations of the posture, beginning with

an overshoot followed by a gradual decline towards

a stable endpoint. In contrast, the trajectories

generated by the Elman controller tend to terminate

in a drifting hand position, indicating a constant

error output that slowly accumulates. The Elman

controller seems not to be able to compensate for

errors that occurr after the target is reached.

Figure 5: End-point stability. A: Trajectories generated by

a feed-forward ANN variant after 110 time steps (see also

Fig. 4B). B: Trajectories generated by an Elman ANN

variant after 110 time steps (see also Fig. 4D).

4 DISCUSSION

We have shown that goal-directed movement of a

ICFC 2010 - International Conference on Fuzzy Computation

224

human-like limb consisting of arm and shoulder-

girdle can be modelled by a comparatively simple

closed-loop control schema that comprises small

neural network modules and physiological

movement synergies.

In classical studies, only artificial or reduced data

have been used as a basis for the training of neural

networks for motor control (e.g., Massone and Bizzi,

1989, Kawato, et al., 1990, Massone and Myers

1994, Karniel and Inbar, 1997). More recent efforts

to model reaching movements based on ANNs do

take a physiologically oriented approach (Koike, et

al., 2006, Choi, et al., 2009) but still somewhat

neglect the importance of motor primitives or

synergies.

In contrast, numerous studies find evidence in

favor of a modular organization of the nervous

system (e.g. Mussa-Ivaldi, et al., 1994, d'Avella, et

al., 2006). Although these studies propose potential

CNS structures that might be important for motor

primitives, these studies often keep silent with

regard to more concrete neural models and how

exactly movement modules might be combined in a

task- or goal-dependent manner in order to produce

meaningful behavior.

The approach presented here tries to

accommodate both aforementioned aspects: We

combine a connectionist approach based on ANNs

with experimentally observed movement synergies

during a natural reaching task. Combining several

DoFs within one synergies and thereby reducing the

complexity of the control problem allows us to

exploit a bijective mapping between movement

synergy space and task space.

Comparative evaluation of the two controllers

indicates that, for the present problem, the recurrent

Elman network is less appropriate, owing to

insufficient end-point stability. Given, that the

context layer could be interpreted as an internal

model, and that internal models are assumed to be an

important computational element central to nervous

motor control (Wolpert & Ghahramani, 2000), this is

somewhat surprising.

Another notable aspect of the control schema

presented here is the low number of necessary

neuronal units. A feed-forward network with five

hidden units seems to be sufficient for the task of

accurately controlling three movement synergies.

There are two possible explanations for this: On the

one hand, the dissociation of the neuronal substrate

into two distinct modules, i.e. into a controller ANN

and a synergy network, might be more efficient that

a monolithic architecture of similar size. On the

other hand, the approach described here is solely

based on joint angle kinematics and neglects a

further potential source of complexity:

transformation of movement kinematics into a

muscle activation pattern. Again, this transformation

is a one-to-many mapping and might exacerbate the

necessary computations.

REFERENCES

Atkeson, C. G., Hollerbach, J. M. (1985). Kinematic

features of unrestrained vertical arm movements. The

Journal of Neuroscience 5, 2318 – 2330.

Bernstein, N. (1967). The co-ordination and regulation of

movements. New York: Pergamon Press Ltd.

Bockemühl, T., Troje, N. F., and Dürr, V. (2010). Inter-

joint coupling and joint angle synergies of human

catching movements. Human Movement Science 29,

73 – 93.

Choi, K., Hirose H., Sakurai, Y., Iijima, T., Koike, Y.

(2009). Prediction of arm trajectory from the neural

activities of the primary motor cortex with modular

connectionist architecture. Neural Networks 22, 1214

– 1223.

d’Avella, A., Portone, A., Fernandez, L., Lacquaniti, F.

(2006). Control of Fast-Reaching Movements by

Muscle Synergy Combinations. The Journal of

Neuroscience 26, 7791 – 7810.

Elman, J. L. (1990). Finding Structure in Time. Cognitive

Science 14, 179 – 211.

Flash, T., Hochner, B. (2005). Motor primitives in

vertebrates and invertebrates. Current Opinion in

Neurobiology 15, 660 – 666.

Flash, T., Hogan, N. (1985). The coordination of arm

movements: An experimentally confirmed

mathematical model. The Journal of Neuroscience, 5,

1688 – 1703.

Karniel A., Inbar G. (1997). A model for learning human

reaching movements. Biological Cybernetics 77, 173 –

183.

Kawato, M., Maeda Y., Uno, Y., Suzuki R. (1990).

Trajectory formation of arm movement by cascade

neural network model based on minimum torque-

change criterion. Biological Cybernetics 62, 275 –

288.

Koike, Y., Hirose, H., Sakurai, Y., Iijima, T. (2006).

Prediction of arm trajectory from a small number of

neuron activities in the primary motor cortex.

Neuroscience Research 55, 146 – 153.

Levenberg, K. (1944). A method for the solution of certain

nonlinear problems in least squares. Quarterly Journal

of Applied Mathematics 2, 164 – 168.

Marquardt, D. W. (1963). An algorithm for least-squares

estimation of nonlinear parameters. Siam Journal on

Applied Mathematics 11, 431 – 441.

Massone, L., Bizzi, E. (1989). A neural network model for

limb trajectory formation. Biological Cybernetics 61,

417 – 425.

A MINIMAL CONTROL SCHEMA FOR GOAL-DIRECTED ARM MOVEMENTS BASED ON PHYSIOLOGICAL

INTER-JOINT COUPLINGS

225

Massone, L., Myers, J. (1994). A Neural Network Model

of an Anthropomorphic Arm. IEEE Transactions on

Systems, Man, and Cybernetics [B] 26, 719 – 732.

Mussa-Ivaldi, F. A., Giszter, S. F., Bizzi, E. (1994). Linear

combinations of primitives in vertebrate motor control.

Proceedings of the National Academy of Sciences of

the United States of America 91, 7534 – 7538.

Ting, L. H., McKay, J. L. (2007). Neuromechanics of

muscle synergies for posture and movement. Current

Opinion in Neurobiology. 17, 622 – 628.

Todorov, E. (2004). Optimality principles in sensorimotor

control. Nature Neuroscience 7, 907 – 915.

Uno, Y., Kawato M., Suzuki R. (1989). Formation and

control of optimal trajectory in human multijoint arm

movement. Biological Cybernetics 61, 89 – 101.

Wolpert, M., Ghahramani, Z. (2000). Computational

principles of movement neuroscience. Nature

Neuroscience 3, 1212-1217.

ICFC 2010 - International Conference on Fuzzy Computation

226