
EMBEDDED INCREMENTAL FEATURE SELECTION
FOR REINFORCEMENT LEARNING
Robert Wright
1
, Steven Loscalzo
1,2
and Lei Yu
2
1
Information Directorate, Air Force Research Lab, Rome, NY, U.S.A
2
Department of Computer Science, Binghamton University, Binghamton, NY, U.S.A.
Keywords:
Reinforcement learning, Feature selection, Neuroevolution.
Abstract:
Classical reinforcement learning techniques become impractical in domains with large complex state spaces.
The size of a domain’s state space is dominated by the number of features used to describe the state. Fortu-
nately, in many real-world environments learning an effective policy does not usually require all the provided
features. In this paper we present a feature selection algorithm for reinforcement learning called Incremental
Feature Selection Embedded in NEAT (IFSE-NEAT) that incorporates sequential forward search into neu-
roevolutionary algorithm NEAT. We provide an empirical analysis on a realistic simulated domain with many
irrelevant and relevant features. Our results demonstrate that IFSE-NEAT selects smaller and more effective
feature sets than alternative approaches, NEAT and FS-NEAT, and superior performance characteristics as the
number of available features increases.
1 INTRODUCTION
Reinforcement learning (RL) is a popular technique
for many agent-related problems such as robot con-
trol, game playing, and system optimization (Sutton
and Barto, 1998). In such problems, an agent strives
to learn a policy for selecting actions based on its
current state, by performing actions and receiving re-
wards for the actions it tries. The most common ap-
proach to solving an RL problem is to learn a value
function which indicates, for a particular policy, the
long-term expected reward value of a given state or
state-action pair. In domains with large or infinite
state spaces, it is infeasible to represent the value
function explicitly. Instead, a common strategy is
to approximately represent the value function using
some parameterized class of functions. Many func-
tion approximation methods such as radial basis func-
tions (Keller et al., 2006), adaptive tile coding (White-
son and Stone, 2007), and neural networks (Whiteson
and Stone, 2006) have proven successful on problems
with a very small number of state features.
In many real-world problems, the number of fea-
tures with which to describe the states of the environ-
ment can be quite large. When the number of features
is large, existing function approximation methods are
not only computationally prohibitive, but also prone
to over-fitting due to the so-called “curse of dimen-
sionality” - the size of the state space grows exponen-
tially as the number of state features increases. For-
tunately, among many possible features, a large por-
tion of them may be irrelevant or redundant regard-
ing learning a policy. Determining which subset of
features should be used in order to generate the best
performance for the learning task is challenging for
either a domain expert or a learning agent.
This work is about automated feature selection for
RL. Although feature selection has been extensively
studied for supervised learning (Guyon and Elisseeff,
2003; Liu and Yu, 2005), existing methods are either
inapplicable or impractical in the RL setting. Filter
methods rely on training data, which is not available
in RL, to select features. Wrapper methods require re-
peatedly executing a learning algorithm on each can-
didate feature subset, and are impractical for RL due
to their prohibitively high computational and sample
cost. A promising approach is to embed feature selec-
tion into the training process of a learning algorithm.
However, the embedded approach has to be tailored
for the learning algorithm of interest.
In this work, we propose an embedded incremen-
tal feature selection algorithm for a neuroevolutionary
function approximation algorithm NEAT (NeuroEvo-
lution of Augmenting Topologies) (Stanley and Mi-
ikkulainen, 2002), which we call IFSE-NEAT. The
main idea of IFSE-NEAT is to embed incremental
263
Wright R., Loscalzo S. and Yu L..
EMBEDDED INCREMENTAL FEATURE SELECTION FOR REINFORCEMENT LEARNING.
DOI: 10.5220/0003153402630268
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 263-268
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

subset selection into the neuroevolutionary process of
NEAT. Instead of evolving networks with the full set
of features as NEAT does, IFSE-NEAT initializes net-
works with one feature. IFSE-NEAT then iteratively
adds features to the current best network that con-
tributes most to its performance improvement while
evolving the weights and topology of that network.
Prior to this work, feature selection for reinforce-
ment learning has focused on linear value function ap-
proximation (Kolter and Ng, 2009; Parr et al., 2008)
and model-based RL algorithms (Kroon and White-
son, 2009). For neuroevolution algorithms such as
NEAT, only random search has been explored (White-
son et al., 2005). In this light we can see that IFSE-
NEAT is a novel approach in feature selection for RL.
Our experimental study has shownseveral promis-
ing results for IFSE-NEAT.We find that the algorithm
is nearly unaffected in its ability to select relevant fea-
tures as the number of irrelevant features grows very
large. This, in turn, allows for a better policy to be
derived than NEAT and FS-NEAT. Additionally, by
using only a few relevant features we are able to learn
a good policy while limiting model complexity.
The rest of the paper is organized as follows: Sec-
tion 2 introduces the NEAT algorithm and the pro-
posed IFSE-NEAT algorithm. Section 3 describes the
experimental setup. Section 4 presents and discusses
experimental results. Finally, Section 5 concludes this
work and identifies some future research directions.
2 APPROACH
2.1 NEAT
Neural networks (NNs) are efficient function approx-
imators that can model complex functions to an arbi-
trary accuracy. The drawbacks of using NNs in RL
domains have been that NN design was a difficult
manual process and training was a supervised learn-
ing process. Neuroevolutionary approaches, which
utilize genetic algorithms to automate the process of
training and/or designing NNs, eliminate these draw-
backs allowing NNs to be easily applied to RL do-
mains. NeuroEvolution of Augmenting Topologies
(NEAT) is a novel RL framework based on neuroevo-
lution. By evolving both the network topology and
weights of the connections between network nodes,
NEAT solved typical RL benchmark problems sev-
eral times faster than competing RL algorithms with
significantly less system resources (Stanley and Mi-
ikkulainen, 2002).
However, one limiting issue with NEAT is that it
assumes that all features provided by the environment
are relevant and necessary, and attempts to incorpo-
rate all the features into its solution networks. The
extraneous features will unnecessarily complicate the
networks and severely slow the rate at which NEAT is
able to derive an effectivepolicy. In the following sec-
tion we describe a new algorithm based upon NEAT
that builds a small set of required features while learn-
ing an effective policy.
2.2 Incremental Feature Selection
Embedded in NEAT
To deal with the exponential search space, we adopt
sequential forward search (SFS), an efficient search
strategy which has proven effective in finding near-
optimal subsets in supervised feature selection. Start-
ing from an empty set, SFS iteratively adds one fea-
ture at a time to the current best set until a desired
number of features k are selected. Since in each of
the k iterations, it goes through all N features outside
of the current best set, the time complexity of SFS is
O(kN). Although SFS does not guarantee the optimal
solution, it is capable of selecting relevant features
while keeping irrelevant or redundant features out of
the final subset. The method is particularly suitable
for high-dimensional problems where a large portion
of the features are irrelevant or redundant.
Algorithm 1 provides a basic overview about how
IFSE-NEAT functions and is able to select a mini-
mal set of features. IFSE-NEAT incrementally adds
features to a NN that we call the BACKBONE. The
BACKBONE network utilizes the best discovered fea-
ture set and represents the current best derived policy.
It is persistent through additions of new features to
the feature set and it is what makes IFSE-NEAT an
embedded algorithm as opposed to a straightforward
wrapper algorithm.
Initially, the BACKBONE network consists of
only the output nodes (line 5). Then, for each of
the individual features available, F
q
, a NN is gener-
ated by connecting a single input node to every output
node (line 13). In parallel, or independently, a popu-
lation of networks based upon this single-input base
network is generated. Each network in the popula-
tion share the topology of the base network, but have
randomly generated weights on the edges joining the
nodes. The population of NNs are then evolved via
the standard NEAT algorithm for L generations (lines
17-19). At the end of the NEAT process, the cham-
pion of each population (the network representing the
best policy) is identified. The champions (each corre-
sponding to a candidate feature F
q
) are then compared
against one another to decide the BEST NETWORK
and BEST FEATURE (lines 22-25). It is our hypoth-
esis that the best performing network, BEST NET-
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
264
Algorithm 1: IFSE-NEAT(N,k,L,p).
1: //N: set of all available features
2: //k: number of features to select
3: //L: number of generations to evolve
4: //p: population size
5: BACKBONE ← outputNodes //initialize the BACKBONE
6: SELECTED SET ← null //initialize the selected feature set
7: for i ← 1 : k do
8: BEST NETWORK ← null
9: BEST FEATURE ← null
10: //iterate through all candidate features outside SELECTED SET
11: for q ← 1 : N − i do
12: //create new network N
b
based on candidate feature F
q
13: N
b
← COMBINE( F
q
, BACKBONE )
14: //create a population of p networks based upon N
b
15: population ← INITIALIZE-POPULATION(N
b
, p)
16: //evolve population using NEAT for L generations
17: for j ← 1 : L do
18: NEAT-EVOLVE(population)
19: end for
20: //select the champion from population
21: champion ← BEST-QUALITY(population)
22: if champion > BEST NETWORK then
23: BEST FEATURE ← F
q
24: BEST NETWORK ← champion
25: end if
26: end for
27: Add BEST FEATURE to SELECTED SET
28: BACKBONE ← BEST NETWORK
29: end for
WORK, will point to the most relevant fea-
ture. Therefore, the BEST FEATURE that
produced the BEST NETWORK is then added
to the SELECTED SET (line 27), and the
BEST NETWORK becomes the BACKBONE
(line 28) for subsequent iterations where the algo-
rithm will determine the next features to add to the
feature set.
In the subsequent iterations the remaining features
are independently combined with the BACKBONE
network and then re-evaluated. As in the first feature
selection iteration, new populations of NNs, random
variations of the base networks, are again evolved by
NEAT for L generations. The algorithm stops once a
desired number of features are selected. Alternatively,
the algorithm can stop when one of the populations
produces a network that represents a suitable solution
to the problem.
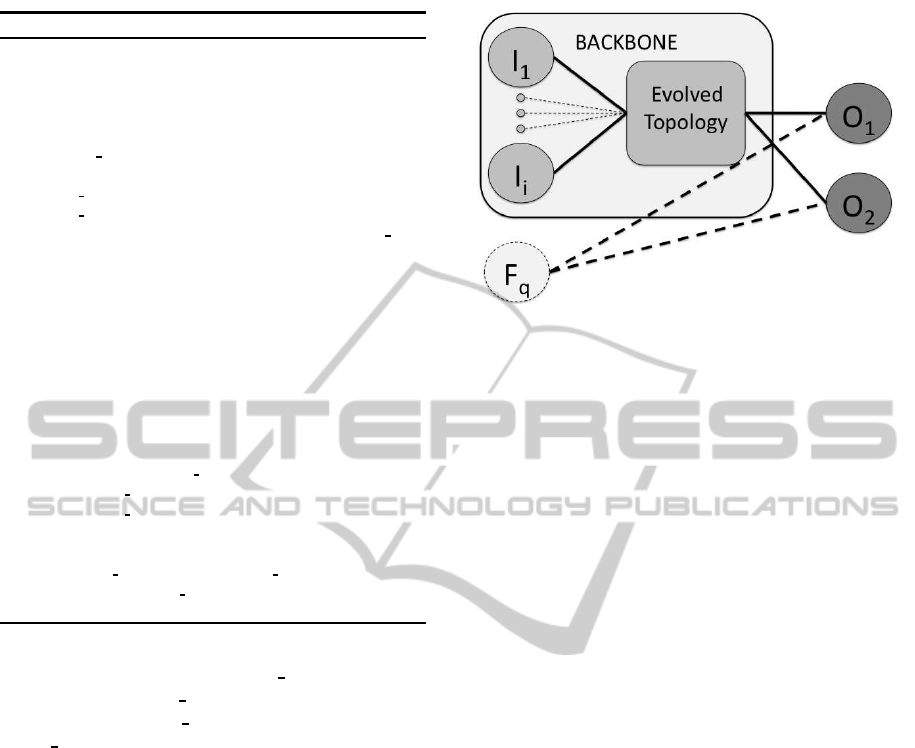
The process for combining the BACKBONE net-
work, COMBINE(F
q
,BACKBONE) (line 13), is illus-
trated in Figure 1. In this process a new base network
N
b
is created for a candidate feature F
q
by connecting
F
q
to each of the output nodes. The weights of these
new edges are assigned zero to preserve the policy
of the BACKBONE network. Preserving the policy
of the BACKBONE network bootstraps the successive
networks and improves IFSE-NEAT’s ability to deter-
Figure 1: This figure illustrates how a candidate feature is
incorporated into the current BACKBONE network to create
a new base candidate network, N
b
. The new feature F
q
is
introduced to the network and is provided connections, the
dashed lines, to every output node. BACKBONE in this
figure represents the best evolved solution network using
only the previously selected features.
mine the relevance of potential new features.
Analysis of Algorithm 1 shows that time complex-
ity of IFSE-NEAT is O(kN) times the NEAT process,
which itself is dependent on the population size p
and the number of generations L. In practice, how-
ever, we can do better than this. For the first few se-
lected features, L can be very small and the algorithm
can still identify relevant features, allowing a signifi-
cant speedup to roughly O(N) times NEAT. Once the
BACKBONE network is reasonably fit, L must be in-
creased to allow new features enough time to have an
impact in the more complex network.
3 EXPERIMENTAL SETUP
We analyze the performance of our IFSE-NEAT al-
gorithm from two perspectives: (i) the quality of the
derived policy, and (ii) the ability of the algorithm to
select relevant features. We measure the quality of the
derived policy by a problem-specific fitness function.
The composition of the selected subset in terms of
the fraction of relevant features among selected ones
quantifies an algorithm’s ability to select a good fea-
ture subset. Finally, we verify that the performance of
our algorithm (measured by the above metrics) does
not degrade as the number of irrelevant features in-
creases.
We compare IFSE-NEAT to the baseline NEAT as
well as FS-NEAT, a competing feature selection algo-
rithm we describe in Section 3.1. All three algorithms
are evaluated in a challenging race track domain that
is capable of providing many relevant and irrelevant
EMBEDDED INCREMENTAL FEATURE SELECTION FOR REINFORCEMENT LEARNING
265

features for the algorithms to work with. The details
of this environment as well as the specific parameters
used by the algorithms are given in Section 3.2.
3.1 FS-NEAT
Feature Selective NEAT, or FS-NEAT, is an em-
bedded feature selection algorithm within the NEAT
framework (Whiteson et al., 2005). One limiting as-
sumption standard NEAT makes, discussed in Sec-
tion 2.1, is that all input features are relevant and
are fully incorporated into all solution networks. FS-
NEAT assumes that few features are actually relevant.
Networks are initialized with only a single connection
between a randomly selected pair of input and out-
put nodes. Through subsequent mutations other input
nodes may add a connection to the rest of the network
and hence be selected into the model.
3.2 RARS
We conducted our experimental analysis using ver-
sion 0.91 2 of the Robot Auto Racing Simulator
(RARS)
1
. RARS provides a detailed physical simu-
lation of a racetrack and vehicles and allows users to
define their own artificial agents to control the racers.
The goal of the simulation is to learn a path around
the track that covers the most distance in a limited
time while minimizing damage received by the car.
Damage is calculated by RARS based on the amount
of time the car spends off the track. The racers are
controlled by supplying a desired speed and direction
at every time step in the simulation.
Table 1: Different problems used in the RARS experiments
broken down by the number of relevant, irrelevant, and total
number of features.
Relevant Irrelevant Total
5 5 10
5 25 30
5 45 50
5 95 100
We implemented a rangefinder system in the sim-
ulation to provide vehicle position information to the
learning algorithm as in Figure 2. In our experiments
we placed N range sensors evenly around the front of
the car as in (Whiteson et al., 2005), starting from the
left side of the car and finishing at the right to provide
a full view of the track. The range finders, together
with the velocity of the car, are used by the learner to
1
http://rars.sourceforge.net/
provide two continuous control outputs, correspond-
ing to the desired speed and direction of the car.
To make the RARS environment challenging from
a feature selection point of view we added irrelevant
features to the set. Irrelevant features simply return a
random value in [-1,1]. We developed several chal-
lenging problems with different combinations of rel-
evant and irrelevant features as shown in Table 1.
These combinations allow us to examine the robust-
ness of each of the three algorithms in comparison
w.r.t. increasing numbers of irrelevant features.
All three algorithms tested are neuroevolution-
ary algorithms that require a fitness function to pro-
vide the feedback that guides learning. We adopt
the fitness function used by (Whiteson et al., 2005),
S = 2d − r, where d is the distance the car has trav-
eled from the start and r is the amount of damage re-
ceived. Trials end after the learner either has observed
2000 time steps or the car registers too much damage.
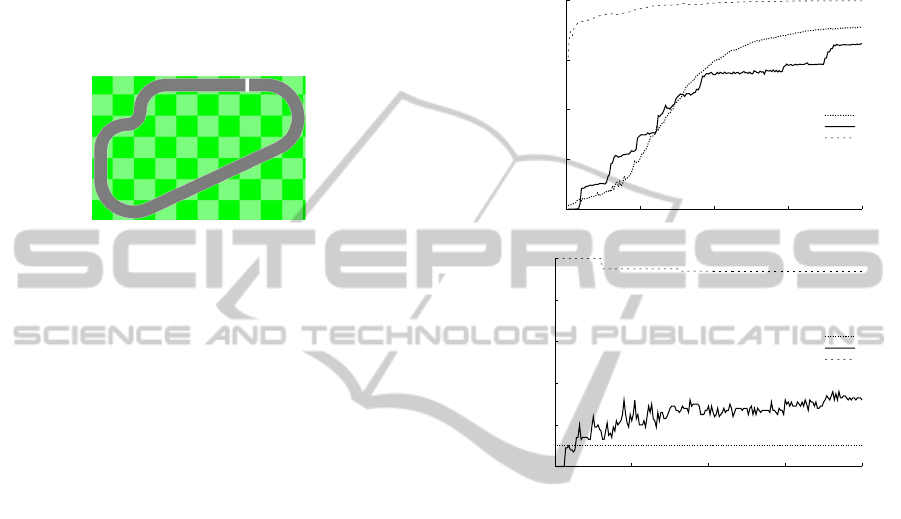
All experiments took place on the clkwis.trk track
that is bundled in the RARS package, shown in Fig-
ure 3. This track was selected because it exhibits sev-
eral driving scenarios such as straightaways, turns and
an S-curve. The experiments were conducted in the
RARS environment according to the following setup.
Figure 2: Rangefinders (dashed lines) extending outwards
from the vehicle to the edges of the track (solid lines) en-
code vehicle location information in this environment.
• Three algorithms were tested, NEAT, FS-NEAT,
and IFSE-NEAT
• For each tested combination of features 10 runs
were conducted with each algorithm, results pre-
sented are the average of these 10 runs.
• Each run lasted 200 generations
• IFSE-NEAT split the 200 generations into
five L(·) periods with L(1) = 3, L(2) =
7, L(3) = 20, L(4) = 50, L(5) = 120
• The NEAT population size was set to 100
We set the number of generationsallowed to 200 since
the algorithms appeared to converge by that point and
there was no need to carry the experiment further. The
particular values of the L(·) function are not impor-
tant, and we experimented with other values which
yielded similar results.
All three algorithms in comparison rely on NEAT
for generation of the neural networks to allow learn-
ing. In our experiments we make use of Another
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
266
NEAT Java Implementation (ANJI) for the NEAT al-
gorithm (James and Tucker, 2004). We followed the
settings given in (Whiteson et al., 2005) of 0.10 and
0.02 for add-connection and add-neuron respectively
to set the parameters for the FS-NEAT algorithm. For
NEAT, and IFSE-NEAT we set the add-connection
mutation probability to 0.02 and the add-neuron mu-
tation to 0.01. In our experiments we found the pa-
rameters used with FS-NEAT to be too aggressive for
NEAT and IFSE-NEAT.
Figure 3: A top-down view of the clkwis track used in the
experiments.
4 RESULTS
Figure 4a shows the results of running the three algo-
rithms for the problem with 5 relevant features and
45 irrelevant features as the algorithms search for
the optimal policy. Fitness of the derived policies is
measured in terms of the value of the fitness func-
tion defined in Section 3.2. We can see that IFSE-
NEAT converges to the best fitness of the three algo-
rithms, and this convergence occurs at around gener-
ation 50. Both NEAT and FS-NEAT exhibit a slower
rate of convergence than IFSE-NEAT. In this situa-
tion, NEAT is limited by the need to assign correct
weights to many features. Since all available fea-
tures are used in the NEAT neural network, NEAT has
to evolve through many generations to find the right
weights for links associated with the relevant features
while keeping weights for irrelevant features low in
order to limit their impact on the network output. The
FS-NEAT algorithm suffers from its random search
policy. Since there are many irrelevant features in the
problem, they have a higher chance of being included
in the network than a relevant feature does, causing
the algorithm to be slow to learn an effective policy.
In Figure 4b we see the composition of the se-
lected subsets by the three algorithms. IFSE-NEAT
clearly has the highest percentage of relevant features
per selected group, at around 90% on average. This
number begins at 100% for 1 selected feature and
slowly decreases as features are added to the set. Fig-
ure 4a shows that IFSE-NEAT achieves optimal fit-
ness early, and then even relevant features do not ap-
pear helpful, causing some irrelevant features to be
incorrectly selected in some of the 10 runs of the al-
gorithm. FS-NEAT slowly adds new features to the
set, many of which are irrelevant, causing low scores
in both measures. It should be noted that IFSE-NEAT
and FS-NEAT select around 5 features by the 200
th
generation in all tested settings.
(a)
0
5000
10000
15000
21000
0 50 100 150 200
Fitness
Generations
NEAT
FS-NEAT
IFSE-NEAT
(b)
0
20
40
60
80
100
0 50 100 150 200
Relevant/Selected Features (%)
Generations
NEAT
FS-NEAT
IFSE-NEAT
Figure 4: Two performance metrics: fitness (a) and the frac-
tion of relevant features among the selected ones (b), for
NEAT, FS-NEAT, and IFSE-NEAT across 200 generations
on the problem with 5 relevant features and 45 irrelevant
features.
We now further study how the three algorithms
scale with an increasing number of irrelevant fea-
tures. Figure 5b shows the fraction of relevant fea-
tures among the selected ones by each algorithm. We
can see that for each of the problems, IFSE-NEAT se-
lects on average at least four relevant features in five
feature selection steps. This validates our feature
ranking and selection criteria, and supports the con-
sistently good fitness values seen in Figure 5a. As
predicted, NEAT’s fitness degrades as the number of
irrelevant features increases and the fraction of rele-
vant features decreases. It always includes all the ir-
relevant features, which increases the complexity of
the networks and slows down learning. FS-NEAT’s
fitness shows a variable trend caused by the random
selection mechanism. Despite starting with more ir-
relevant features in the problem with 50 features, the
fitness of the final policy actually improved over the
problems with 10 and 25 features, as shown in Fig-
EMBEDDED INCREMENTAL FEATURE SELECTION FOR REINFORCEMENT LEARNING
267

(a)
0
5000
10000
15000
21000
10 30 50 100
Fitness
Available Features
NEAT
FS-NEAT
IFSE-NEAT
(b)
0
20
40
60
80
100
10 30 50 100
Relevant/Selected Features (%)
Available Features
NEAT
FS-NEAT
IFSE-NEAT
Figure 5: Two performance metrics: fitness (a) and the frac-
tion of relevant features among the selected ones (b), for
NEAT, FS-NEAT, and IFSE-NEAT at the 200th generation
across 4 problems with 5 relevant features and 5, 25, 45,
and 95 irrelevant features.
ure 5a. This is most likely the result of the net-
work weights being randomly improved by chance
and more trials should remove this effect.
5 CONCLUSIONS AND FUTURE
WORK
In this work, we have developed an embedded fea-
ture selection algorithm which incorporates a sequen-
tial forward search into the neuroevolutionary func-
tion approximation method NEAT for reinforcement
learning. Our results demonstrate the effectiveness of
IFSE-NEAT at identifying relevant features and elim-
inating irrelevant ones. This ability enables IFSE-
NEAT to converge upon higher quality policies us-
ing simpler networks in fewer generations than either
NEAT or FS-NEAT.
These contirbutions do come at a cost. Although
IFSE-NEAT is more efficient than wrapper methods,
the incremental search for relevant features adds sig-
nificant computational cost when compared to the
other NEAT variants. Possible future directions in-
clude investigatingthe parallelization of the algorithm
to help mitigatethis cost, and further study on the gen-
eralization ability of the simple NN solutions found
by IFSE-NEAT.
REFERENCES
Guyon, I. and Elisseeff, A. (2003). An introduction to vari-
able and feature selection. Journal of Machine Learn-
ing Research, 3:1157–1182.
James, D. and Tucker, P. (2004). A comparative analysis of
simplification and complexification in the evolution of
neural network topologies. In Proceedings of the 2004
Conference on Genetic and Evoluationary Computa-
tion (GECCO-04). Springer.
Keller, P., Mannor, S., and Precup, D. (2006). Automatic
basis function construction for approximate dynamic
programming and reinforcement learning. In Proceed-
ings of the the 23rd International Conference on Ma-
chine Learning, pages 449–456.
Kolter, J. Z. and Ng, A. Y. (2009). Regularization and
feature selection in least-squares temporal difference
learning. In Proceedings of the 26th International
Conference on Machine Learning (ICML09), pages
521–528.
Kroon, M. and Whiteson, S. (2009). Automatic feature se-
lection for model-based reinforcement learning in fac-
tored mdps. In Proceedings of the International Con-
ference on Machine Learning and Applications, pages
324–330.
Liu, H. and Yu, L. (2005). Toward integrating feature
selection algorithms for classification and clustering.
IEEE Transactions on Knowledge and Data Engineer-
ing (TKDE), 17(4):491–502.
Parr, R., Li, L., Taylor, G., Painter-Wakefield, C., and
Littman, M. L. (2008). An analysis of linear models,
linear value-function approximation, and feature se-
lection for reinforcement learning. In Proceedings of
the 25th International Conference on Machine Learn-
ing (ICML08), pages 752–759.
Stanley, K. O. and Miikkulainen, R. (2002). Efficient rein-
forcement learning through evolving neural network
topologies. In Proceedings of the Genetic and Evolu-
tionary Computation Conference (GECCO 02), pages
569–577.
Sutton, R. and Barto, A. (1998). Reinforcement learning:
an introduction. MIT Press.
Whiteson, S. Taylor, M. E. and Stone, P. (2007). Adaptive
tile coding for value function approximation. Techni-
cal report, University of Texas at Austin.
Whiteson, S. and Stone, P. (2006). Evolutionary function
approximation for reinforcement learning. Journal of
Machine Learing Research, 7:877–917.
Whiteson, S., Stone, P., and Stanley, K. O. (2005). Au-
tomatic feature selection in neuroevolution. In Pro-
ceedings of the Genetic and Evolutionary Computa-
tion Conference (GECCO 05), pages 1225–1232.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
268
