A NETWORK MODEL FOR PRICE STABILIZATION
Jun Kiniwa
Department of Applied Economics, University of Hyogo, 8-2-1 Gakuen nishi-machi, Nishi-ku, Kobe-shi, 651-2197 Japan
Kensaku Kikuta
Department of Strategic Management, University of Hyogo, 8-2-1 Gakuen nishi-machi, Nishi-ku, Kobe-shi, 651-2197 Japan
Keywords:
Multiagent model, Price determination, Auction theory, Consensus problem.
Abstract:
We consider a simple network model for economic agents where each can buy commodities in the neighbor-
hood. Their prices may be initially distinct in any node. However, by assuming some rules on new prices, we
show that the distinct prices will be converged to unique by iterating buy and sell operations. If we consider
the price determination process as a kind of consensus problem, we can apply the stabilization proof to it.
So we first present a naive protocol in which each agent always offers half of the difference between his own
price and the lowest price in the neighborhood, called max price difference. Then, we consider game theoretic
price determination in two ways, that is, by using different payoff functions. Finally, we propose a protocol in
which each agent makes a bid uniformly distributed over the max price difference.
1 INTRODUCTION
Conventionally, the topics of price determinationhave
been discussed in the context of microeconomics ap-
proach (J. E. Stiglitz, 1993). A famous model, supply
and demand curves, has been used as an abstract, the-
oretical method which explains a price equilibrium.
However, for example, there is no distance concept in
the model. To know a detailed process to the equilib-
rium, we need more sophisticated model, e.g., multia-
gent approach, which gives us another insight into the
price determination.
We construct a price determination model by ap-
plying the idea of stabilization to the multiagent ap-
proach. The self-stabilization (S. Dolev, 2000) has
been originally studied as the recovery from transient
faults in distributed systems. From any initial state,
self-stabilizing algorithms eventually lead to a legiti-
mate state without any aid of external actions. In par-
ticular, a self-stabilizing consensus algorithm is as-
sociated with the price determination because every
agent eventually has the same value.
We show a network model consisting of nodes and
edges as cities and their links to neighbors, respec-
tively. Each node contains an agent which represents
people in the city. Any interaction among agents is
governed by micro-rules, that is, the agents who want
to buy a commodity make bids to their neighboring
nodes. Then, the agents who want to sell the com-
modity accept the highest bid, like an auction (V. Kr-
ishna, 2002). By iterating these rules, the prices will
reach an equilibrium.
First, we present a naive protocol in which each
agent always offers a fixed price without consider-
ing other bidders’ strategies. Then, we analyze the
stabilization time of the protocol for a special case.
Next, we consider game theoretic price determination
in two ways, that is, by using different payoff func-
tions. Finally, we propose a protocol in which each
agent offers a random price and show that it stabilizes
with high probability.
2 MODEL
Our system can be represented by a connected net-
work G = (V,E), consisting of a set of n nodes V and
edges E, where the nodes represent cities and a pair
of neighboring nodes (cities) is linked by an edge. We
assume that each node i ∈ V has a commodity and its
initial price may be different. Let N
i
be a set of neigh-
boring nodes of i ∈ V, and let N
+
i
= N
i
∪{i}. Let P
i
(t)
be the commodity price in the node i at time t. It is
also denoted by P
i
if time t is not important. We say
that the price P
i
(t) is maximal if P
i
(t) ≥ P
j
(t) for any
394
Kiniwa J. and Kikuta K..
A NETWORK MODEL FOR PRICE STABILIZATION.
DOI: 10.5220/0003153803940397
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 394-397
ISBN: 978-989-8425-41-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

j ∈ N
i
. Each node i ∈ V has exactly one representative
agent a
i
who always stays at i and can buy commodi-
ties in the neighborhood N
i
, where the buy operation
is executed as follows.
First, each agent a
i
compares the commodity price
P
i
(t) with P
j
(t) for j ∈ N
i
. If node j ∈ N
i
has the
cheapest commodity in N
i
with P
i
(t) > P
j
(t), the
agent a
i
wants to buy it from the node j. (Otherwise,
that is, there is no node j ∈ N
i
with P
i
(t) > P
j
(t), agent
a
i
wants to buy it in the self node i.) We call such
P
i
(t) − P
j
(t) a max price difference. Then, agent a
i
submits a bid to node j containing some price in ac-
cordance with a protocol. After accepting bids from
N
j
, agent a
j
contracts with exactly one agent who
submitted the highest price. Then, a
j
sells the com-
modity to the contracted agent and sets P
j
(t+1) to the
highest price. We ignore the carrying time of com-
modities and focus on the change of prices. In this
way, at every time, any price is updated if necessary.
We assume a synchronous model, that is, every
agent periodically (for each round) exchanges mes-
sages and knows the states of neighboring agents.
3 NAIVE PROTOCOL
In this section, we consider a naive protocol, called
HalfBid, in which each agent always offers half of
the max price difference. Here, we focus on a star,
the part of a network G, with a center node c.
HalfBid
• Each agent a
j
makes a bid with an integer price
P
c
(t) +

P
j
(t) − P
c
(t)
2

to node c ∈ N
+
j
which has the lowest-priced com-
modity in N
+
j
. The agent a
c
contracts with the
neighboring a
j
who has submitted the highest bid.
That is, the commodity price at time t + 1 is
P
c
(t + 1) := P
c
(t) + max
j∈N
c

P
j
(t) − P
c
(t)
2

• If P
c
(t) is maximal and a
c
accepts no bidding from
N
c
, the price at time t + 1 will be cut to
P
c
(t + 1) := P
c
(t) − max
j∈N
c

P
c
(t) − P
j
(t)
2

• If several agents make bids to node c with the
same highest price, agent a
c
contracts with one
of them with equal probability.
1
0
2
3
bid=60
bid=30
bid=80
(a)
1
0
2
3
(b)
Figure 1: An illustration of naive protocol HalfBid.
Example 1. Figure 1 shows an example of our net-
work system consisting of 4 nodes V = {0,1,2, 3}.
At time t, the prices of commodities are (P
0
(t),P
1
(t),
P
2
(t),P
3
(t)) = (50,10,110,70) as shown in Fig-
ure 1(a). Each agent a
c
wants to buy the com-
modity if its price is lower than P
c
(t), i.e., P
c
(t) >
min
j∈N
c
P
j
(t). Thus, agent a
2
makes a bid to node
0 with price 50 + (110 − 50)/2. Likewise, agents a
0
and a
3
make bids to node 1 and node 0, respectively.
Then, a
2
’s bid and a
0
’s bid are successful, a
2
(resp.
a
0
) makes a contract with a
0
(resp. a
1
). At time t + 1,
the prices become (80,30,80,70) as shown in Fig-
ure 1(b). Since node 2 was maximal and no bid was
submitted, the price is cut to 80 at time t + 1. ⊓⊔
Let C
t
⊆ V be the set of nodes that have updated
their prices from time t to t + 1. Let the highest price
be P
max
(t) = max
i∈C
t
P
i
(t), and the lowest price be
P
min
(t) = min
i∈C
t
P
i
(t). The following lemma states
that prices continue to move until every node has the
same price.
Lemma 1. The protocol HalfBid is deadlock-free.
That is, there exist some nodes in C
t
as long as the
unique price is not determined.
Proof sketch. The lemma is proved by contradiction.
⊓⊔
Lemma 2. Let diff(t) = max
i∈C
t
P
i
(t)−min
i∈C
t
P
i
(t).
As long as C
t
6= φ, we have
diff(t) > diff(t + 1).
Proof. First, we consider a node i 6∈ C
t
. Since agent
a
i
does not make any bid to other nodes, there is no
change in price. Thus, max
j∈N
i
⌊
P
i
(t)−P
j
(t)
2
⌋ = 0 holds.
Next, suppose that a node has the maximum price
in C
t
. Since no neighboring nodes make bids to such
a node, the price will be down at time t + 1. If a node
has the minimum price in C
t
, there is a neighboring
agent who makes a bid to the node. Thus, the price
will be up at time t + 1. Let P
max2
(t) be the second
maximum price among the nodes in C
t
. Then, the
price will not exceed P
max
(t) at time t + 1 because
P
max2
(t) goes maximumly up only when it accepts an
offer from P
max
(t). Even if it occurs, the increase is at
most the half of the difference between them. Thus,
A NETWORK MODEL FOR PRICE STABILIZATION
395

we have
P
max
(t) > P
max2
(t + 1), P
max
(t) > P
max
(t + 1).
On the other hand, the node with P
min
(t) accepts a
new bid and the price P
min
(t) goes up at time t + 1.
Let P
min2
(t) be the second minimum price among the
nodes in C
t
. Then, it maximumly decreases without
any offers only when it is linked with the node with
P
min
(t). Then, we have
P
min
(t) ≤ P
min2
(t + 1), P
min
(t) < P
min
(t + 1).
Thus, diff(t) > diff(t + 1) holds. ⊓⊔
Theorem 1. Our protocol will eventually stabilize the
price. ⊓⊔
In the sequel, we analyze the stabilization time of
a path (1,...,n).
Theorem 2. If network G is a path, the stabilization
time of our HalfBid is 2τ rounds, where τ satisfies
(
3
4
)
τ
(
1
3
)
n/2+1

τ
n/2+1

n/2+1
= 1.
Proof. We call the price differencebetween neighbor-
ing nodes a gap, and call the gaps as 1st gap, 2nd gap
... in the ascending order of the nodes. Let d
i
(t) be
the difference of the i-th gap at time t, where t means
every other time here. Then, we have the following
recurrences.
d
i
(t + 1) =
1
4
d
i−1
(t) +
1
2
d
i
(t) +
1
4
d
i+1
(t) (1)
d
1
(t + 1) =
1
2
d
1
(t) +
1
4
d
2
(t) (2)
d
h
(t + 1) =
1
2
d
h
(t) +
1
4
d
h−1
(t) (3)
Let S
h− j
(t) =
∑
h− j
i= j+1
d
i
(t) and S
h
(0) = D. Summing
(1) from i = 1 to h by using (2) and (3) gives
S
h
(t + 1) = S
h
(t) −
1
4
(d
1
(t) + d
h
(t)).
Since d
1
(t) + d
h
(t) = S
h
(t) − S
h−1
(t), we have
S
h
(t + 1) =
3
4
S
h
(t) +
1
4
S
h−1
(t). (4)
By using a generating function, S
h
(t) is given by
D(3/4)
t
h
∑
k=0
(1/3)
k

t
k

= D(3/4)
t
{(1+1/3)
t
− (1/3)
h+1

t
h+ 1

− O(1/3
h+2
)}
≤ D
(
1−

3
4

t

1
3

n/2+1

t
n/2+ 1

n/2+1
)
because h ≈ n/2. Hence, S
h
(t) = 0 gives
(
3
4
)
t
(
1
3
)
n/2+1

t
n/2+1

n/2+1
= 1. Since it takes 2t
rounds until convergence, the lemma follows. ⊓⊔
4 GAME THEORETIC PRICE
DETERMINATION
In this section, we consider how to determine a bid-
ding price in two ways by using Bertrand model(J. E.
Stiglitz, 1993). Here, as customary, we use “Player”
instead of “agent”.
4.1 Payoff with Second Price
For simplicity, we consider a three-node path (1,c)
and (c,2). Suppose that both Player 1 (i.e., agent a
1
)
at node 1 and Player 2 (i.e., agent a
2
) at node 2 buy
a commodity in the center node c at time t + 1. Let
q
1
and q
2
be the bidding prices of Player 1 and Player
2, respectively. Then, the payoff of Player 1 is y =
P
1
(t) − q
1
. On the other hand, the payoff of Player 2
is y = P
2
(t) − q
2
in the same situation.
As the price goes up, the payoffs of the players go
down. In addition, Player 1 (resp. Player 2) regrets if
the difference q
1
− q
2
(resp. q
2
− q
1
) is large even if
he gets the commodity. Next, if q
1
= q
2
, both Player 1
and Player 2 get the commodity with probability 1/2.
Thus, the payoff function of Player 1, u
1
(q
1
,q
2
), is
defined as
u
1
(q
1
,q
2
) =



(P
1
− q
1
)/(q
1
− q
2
) q
1
> q
2
(P
1
− q
1
)/2 q
1
= q
2
0 q
1
< q
2
The payoff function of Player 2, u
2
(q
1
,q
2
), is simi-
larly defined.
Now we temporarily assume that q
1
and q
2
are
continuous variables. Then,
∂u
1
∂q
1
= (q
2
− P
1
)/(q
1
− q
2
)
2
= 0
That is, we obtain q
2
= P
1
. Similarly,
∂u
2
∂q
2
= (q
1
− P
2
)/(q
2
− q
1
)
2
= 0
That is, we obtain q
1
= P
2
. Thus, (q
1
,q
2
) = (P
2
,P
1
)
is the Nash equilibrium. This is also true when q
1
and
q
2
are integers.
4.2 Payoff without Second Price
In this section, we define the payoff function of Player
1 and that of Player 2 as follows.
u
1
(q
1
,q
2
) =



P
1
− q
1
q
1
> q
2
(P
1
− q
1
)/2 q
1
= q
2
0 q
1
< q
2
u
2
(q
1
,q
2
) =



P
2
− q
2
q
1
< q
2
(P
2
− q
2
)/2 q
1
= q
2
0 q
1
> q
2
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
396

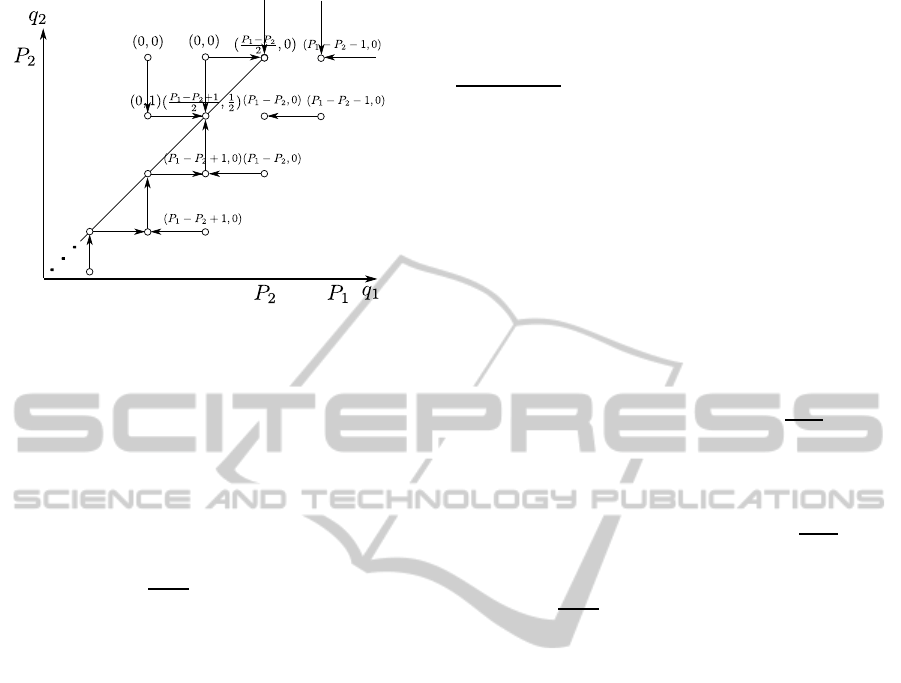
B
C
A
D
E
Figure 2: Payoffs without second price.
Without loss of generality, we assume P
2
(t) ≤
P
1
(t) and every price takes an integer value. By using
the payoff functions, we have payoff values as shown
in Figure 2.
Figure 2 illustrates a q
1
q
2
-space determined by the
payoff functions. A pair of values in a bracket means
(u
1
,u
2
) located at the intersection of the grid, corre-
sponding to integer values of q
1
and q
2
. For example,
at D, a pair of bidding (q
1
,q
2
) = (P
2
,P
2
) produces
payoffs (u
1
,u
2
) = (
P
1
−P
2
2
,0). The horizontal arrows
indicate Player 1’s move, while the vertical arrows in-
dicate Player 2’s move.
If q
1
6= q
2
holds, the payoff of the smaller bid is
0. Thus, their offered prices must be equal like A.
However, since Player 1 wants to increment its bid
because his payoff would be twice. Then, Player 2
wants to raise his bid to the equal value to Player 1
because his payoff would be 0. In this way, Players 1
and 2 move from A to B. After the price has reached
B, Players 1 and 2 have no incentive to move anymore
if (P
1
− P
2
+ 1)/2 ≥ P
1
− P
2
. The price moves to C if
(P
1
− P
2
+ 1)/2 < P
1
− P
2
.
In summary, we obtain the following results.
(1) P
1
− P
2
= 0: (q
1
,q
2
) = (P
2
− 1, P
2
− 1),(P
2
,P
2
)
are the Nash equilibria.
(2) P
1
− P
2
= 1: (q
1
,q
2
) = (P
2
− 1,P
2
− 1),(P
2
,P
2
−
1),(P
2
,P
2
) are the Nash equilibria.
(3) P
1
− P
2
= 2: (q
1
,q
2
) = (P
2
,P
2
− 1),(P
2
,P
2
),
(P
2
+ 1,P
2
) are the Nash equilibria.
(4) P
1
− P
2
≥ 3: (q
1
,q
2
) = (P
2
,P
2
− 1),(P
2
+ 1, P
2
)
are the Nash equilibria.
5 RANDOMIZED PROTOCOL
Based on the consideration in Section 4, we propose
a protocol, called RandomBid, using a price with the
Bertrand model. Again, we focus on a star, the part of
a network G, with a center node c.
RandomBid
• At time t + 1, agent a
i
offers a random integer
price over the range [P
c
,P
i
− 1] to the neighboring
node c with the minimum price P
c
(t)(< P
i
(t)).
• If agent a
c
with maximal P
c
(t) does not accept any
bid from N
c
and its own offer is accepted by node
i, the price P
c
(t) is decreased to the offered price.
• If several agents make bids to node c with the
same highest price at time t, agent a
c
contracts
with one of them with equal probability.
The following lemma states that the agent with a
maximal price will win the contract.
Lemma 3. The agent a
i
with a maximal price will
win the contract with probability at least
P
i
−P
j
P
i
−P
c
, where
agent a
j
has the second maximal price.
Proof. Since only agent a
i
can submit a bid with
range [P
i
− P
j
], it can win the contract with agent a
c
at the rate. Thus, the probability is at least
P
i
−P
j
P
i
−P
c
. ⊓⊔
The above lemma means that the agent a
i
with a
maximal price will win the contract with probability
at least 1− (
P
j
−P
c
P
i
−P
c
)
m
after m rounds.
Theorem 3. Our RandomBid will eventually stabi-
lize the price with high probability. ⊓⊔
6 CONCLUSIONS
In this paper we considered a new network model for
the price stabilization. The model shows that the self-
stabilization has a wide application to various areas.
Our goal is to construct a good multiagent protocol
which enables us to simulate a realistic social sys-
tem. Then, we could analyze and estimate several
economic phenomena.
REFERENCES
J. E. Stiglitz (1993). Principles of micro-economics.
W.W.Norton & Company, New York, 1st edition.
S. Dolev (2000). Self-stabilization. The MIT Press, Mas-
sachusetts, 1st edition.
V. Krishna (2002). Auction theory. Academic Press, San
Diego, 1st edition.
A NETWORK MODEL FOR PRICE STABILIZATION
397