THE METHODOLOGY OF PARALLEL MEMETIC ALGORITHMS

DESIGNING

Wojciech Bo˙zejko

Wrocław University of Technology, Janiszewskiego 11-17, 50-372 Wrocław, Poland

Mieczysław Wodecki

University of Wrocław, Joliot-Curie 15, 50-383 Wrocław, Poland

Keywords:

Metaheuristics, Parallel computing, Evolutionary algorithm, Memetic algorithm.

Abstract:

The paper presents the methodology of parallel algorithm designing based on the memetic approach (Lamarck

and Baldwin evolution theory) making use of speciﬁc properties of the problem and distributed island model.

This approach is presented on the example of the single machine scheduling problem with earliness/tardiness

penalties.

1 INTRODUCTION

The memetic algorithm is an evolutionary approach

based on the process of natural evolution adhering to

the principles of natural selection, crossover and sur-

vival. The Lamarck’s model (Michalewicz, 1994) of

evolution is applied to intensify the optimization pro-

cess. In each generation a certain part of the popu-

lation is replaced by their local minima simulating a

learning effect which can be succeeded by the next

generation as a ’meme’. From the current popula-

tion some subset is drawn. Each individual of this

subset is a starting solution for the local optimization

algorithm. Thus, there are ﬁve essential steps of the

memetic algorithm:

1. selection – choosing some subset of individuals,

so-called parents,

2. crossover – combining parts from pairs of parents

to generate new ones,

3. mutation – transformation that creates a new indi-

vidual by small changes applied to an existing one

taken from the population,

4. learning – an individual is improved (e.g. by a

local optimization),

5. succession – determining the next generation’s

population.

New individuals created by crossover or mutation re-

place all or a part of the old population. The process

of evaluating ﬁtness and creating a new population

generation is repeated until a termination criterion is

achieved.

Similar to the GA, following kinds of paralleliza-

tion are usually applied to memetic algorithms MAs:

• global parallelization,

• independent runs,

• island model,

• diffusion model,

with similar properties as applied to the classic GA.

Additionally, a local search procedure can be par-

allelized in MA. Such an approach is proposed by

(Berger and Barkaoui, 2002) and applied to the Vehi-

cle Routing Problem with Time Windows (VRPTW)

by using a master-slave parallel approach. The master

controls the memetic algorithm execution, synchro-

nizes and handles parent selection while the slaves ex-

ecute genetic operations together with local search in

parallel. Parallel memetic algorithm was also consid-

ered by (Bradwell and Brown, 1999) (asynchronous

MA) and (Tang et al., 2006) (MA based on popula-

tion entropy).

Implementation of algorithms which are based on

multithread multiple-walk searching of the solutions

space are usually coarse-grained application, i.e. they

require sparse communication and synchronization.

These type of algorithms are easy to be applied in

distributed calculation systems, as clusters which ex-

press beneﬁcial efﬁciency-to-price ratio. Apart from

speeding up the calculations, it is possible to improve

643

zejko W. and Wodecki M..

THE METHODOLOGY OF PARALLEL MEMETIC ALGORITHMS DESIGNING.

DOI: 10.5220/0003186006430648

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 643-648

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

quality of obtained results. Search processes can be

either independent or cooperative.

1.1 Independent Searching Threads

In this category we can distinguish two base ap-

proaches:

• Researching of the solution space by using multi-

ple trajectories, which begin from different start-

ing solutions (or different starting populations in

the case of using population-based approaches).

Searching threads can use either the same or dif-

ferent strategies, i.e. the same or different local

search algorithms, the same or different parame-

ters (tabu list length, population size, etc.). Trajec-

tories can cross themselves in one or more places

of the neighborhood graph.

• Parallel researching of subgraphs of a neighbor-

hood graph obtained by decomposition of the

problem into a few subproblems (for example ﬁx-

ing of some variables). Subgraphs of the neigh-

borhood graph are searched concurrently without

crossing search trajectories. We obtain partition-

ing of the neighborhood graph into disjoint sub-

graphs.

The ﬁrst parallel implementation of the tabu

search method based on multiple-walk searching of

the solution space was proposed by Taillard for the

quadric assignment problem (QAP) (Taillard, 1991)

and the job shop problem (Taillard, 1994). The

multiple-walk parallelization strategy based on inde-

pendent searching threads is easy in implementation

and one can obtain good values of the speedup un-

der condition of proper decomposition of the solution

space into searching threads (and their trajectories).

1.2 Cooperative Searching Threads

This model constitutes the most general and promis-

ing type of solution space searching strategy by using

parallel metaheuristics, however it requires knowl-

edge of solving problem speciﬁcity. ’Cooperative’

means here the interchange of information – experi-

ence of searching history up to now. Speciﬁc infor-

mation, which is characteristic for the problem and

the method (i.e. the best solution found so far, elite so-

lutions, the frequency of moves, tabu lists, backtrack-

jump list, subpopulations and their sizes, etc.) has to

be exchanged or broadcasted.

Information shared by search processes can be

stored as global variables kept in the shared memory

or as records in the local memory of the dedicated

central processor which communicates with all other

processors providing them with requested data. In the

model, in which information gathered during moving

along a trajectory is used to improve other trajecto-

ries, not only can one expect convergence of such a

parallel algorithm, but also founding in the same time

a better solution than the parallel algorithm without

communication can take place. In such a case we can

say that cooperative concurrent algorithms constitute

a new class of algorithms in deed.

The ﬁrst heuristic algorithm of this type was asyn-

chronous parallel tabu search algorithm proposed by

Crainic, Toulouseand Gendreau (Crainic et al., 1995).

Packages such as ParSA (Kliewer et al., 1999) of-

fer ready implementations of parallel simulated an-

nealing algorithms based on cooperative searching

threads. The interaction strategy is also very efﬁcient

in implementation of parallel genetic algorithms (in

the sense of obtained solutions). There are plenty of

ready libraries such as POOGAL (Bubak and Sowa,

1999). The majority of cooperative implementations

of parallel genetic algorithm is based on the migra-

tion island model. Each process has its own subpop-

ulation exchanging from time to time a number of

individuals (usually the best – elite) with other pro-

cesses (Bubak and Sowa (Bubak and Sowa, 1999),

Crainic and Toulouse (Crainic and Toulouse, 1998)).

Bo˙zejko (Bo˙zejko, 2010) proposed a parallel path-

relinking metaheuristics based on the parallel scatter

search algorithm.

1.3 The Problem

This paper aim is to present a parallel memetic ap-

proach on the instance of a strongly NP-hard schedul-

ing problem. We additionally assume that the con-

sidered problem has no idle constraint (TWET-no-idle

problem), which means that the machine works with-

out stops. The problem of scheduling with earliness

and tardiness (total weighted earliness/tardiness prob-

lem, TWET) is one of the most frequently consid-

ered in literature. In this problem each job from a

set J = {1, 2,...,n} has to be processed, without in-

terruption, on a machine, which can execute at most

one job in each moment. By p

we represent the exe-

cution time of a job i ∈ J , and by e

and d

we mean

an adequately demanded earliest and latest moment

of the ﬁnishing processing of a job. If scheduling of

jobs is established and C

is the moment of ﬁnishing

a job i, then we call E

= max{0, e

−C

} an earliness

and T

= max{0,C

− d

} a tardiness. The expression

+ w

T is the cost of job execution, where u

and

(i ∈ J ) are nonnegative coefﬁcients of a goal func-

tion. The problem consists in minimizing a sum of

costs of jobs, that is to ﬁnd a job sequence π

∗

∈ Φ

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

644

such that for the goal function

F(π) =

∑

i=1

π(i)

+ w

π(i)

), π ∈ Φ

, (1)

we have

F(π

∗

) = min

π∈Φ

F(π). (2)

This problem is represented by 1||

∑

+ w

) in

literature and it belongs to a strongly NP-hard class

(if we assume u

= 0, i = 1,2, ... ,n, we will ob-

tain a strongly NP-hard problem 1||

∑

- Lenstra

et al. (Lenstra et al., 1977)). Baker and Scudder

(Baker and Scudder, 1990) proved, that there can be

an idle time in an optimal solution (jobs need not

to be processed directly one after another), that is

π(i+1)

− p

π(i+1)

≥ C

π(i)

, i = 1,2,. .. ,n − 1. Solv-

ing the problem amounts to establishing a sequence

of jobs and its starting times. Hoogeven and van

de Velde (Hoogeveen and van de Velde, 1996) pro-

posed an algorithm based on the branch and bound

method. Because of exponentially growing computa-

tion time, this algorithm can be applied only to solve

instances where the number of jobs is not greater than

20. Therefore, in practice almost always approximate

algorithms are used. The best ones are based on artiﬁ-

cial intelligence methods. Calculations are performed

in two stages.

• Determining the scheduling of jobs (with no idle

times).

• Establishing optimal starting times of jobs.

Bo˙zejko and Wodecki (Bo˙zejko and Wodecki, 2005)

proposed a parallel coevolutionary algorithm for the

considered problem.

1.3.1 Block Properties

For the TWET-no-idle problem, each schedule

of jobs can be represented by permutation π =

(π(1),π(2),..., π(n)) of elements of the set of jobs J .

Let Φ

denote the set of all such permutations. The to-

tal cost π ∈ Φ

is F(π) =

∑

i=1

π(i)

), whereC

π(i)

is completed time of the job π(i),C

π(i)

∑

j=1

π( j)

The job π(i) is considered early if it is completed be-

fore its earliest moment of ﬁnishing (C

π(i)

< e

π(i)

), on

time if e

π(i)

≤ C

π(i)

≤ d

π(i)

, and tardy if the job is com-

pleted after its due date (i.e. C

π(i)

> d

π(i)

Each permutation π ∈ Φ

is decomposed

into subpermutations (subsequences of jobs)

B = (B

,. ..,B

) called blocks in π, where:

1. B

= (π(a

),π(a

+ 1),. .. ,π(b

− 1),π(b

)), and

= b

i−1

+ 1, 1 ≤ i ≤ v, a

= 0, b

= n.

2. All the jobs j ∈ B

satisfy the following condi-

tions:

> C

π(b

)

, (C1)

≤ C

π(b

i−1

)

+ p

and d

≥ C

π(b

)

, (C2)

< C

π(b

i−1

)

+ p

. (C3)

3. B

are maximal subsequences of π in which all the

jobs satisfy either Condition C1 or Condition C2

or Condition C3.

By deﬁnition, there exist three types of blocks implied

by either C1 or C2 or C3. To distinguish them, we will

use the E-block, O-block and T-block notions respec-

tively. For any block ϒ in a partition B of permutation

π ∈ Φ

, let

(π) =

∑

i∈ϒ

+ w

). (3)

Therefore, the value of a goal function

F(π) =

∑

i=1

+ w

) =

∑

ϒ∈B

(π). (4)

If ϒ is a T-block, then every job inside is early.

Therefore, an optimal sequence of the jobs within ϒ

of the permutation π (that is minimizing F

(π)) can

be obtained, using the well-known Weighted Short-

est Processing Time (WSPT) rule, proposed by Smith

(Smith, 1956). The WSPT rule creates an optimal se-

quence of jobs in the non-increasing order of the ra-

tios w

. Similarly, if ϒ is an E-block, than an op-

timal sequence of the jobs within can be obtained, us-

ing the Weighted Longest Processing Time (WLPT)

rule which creates a sequence of jobs in the non-

decreasing order of the ratios u

. Partition B of

the permutation π is ordered, if there are jobs in the

WSPT sequence in any T-block, and if there are jobs

in the WLPT sequence in any E-block.

Theorem 1 ((Bo˙zejko et al., 2006)). Let ϒ be an or-

dered partition of a permutation π ∈ Φ

to blocks. If

β ∈ Φ

and F(β) < F(π), so at least one job of some

block of π was moved before the ﬁrst or after the last

job of this block in the permutation β.

Note that Theorem 1 provides the necessary con-

dition to obtain a permutation β from π such, that

F(β) < F(π). Let B = (B

,. ..,B

) be an ordered

partition of the permutation π ∈ Φ

to blocks. If a

job π( j) ∈ B

∈ B), therefore moves which can

improving goal function value consists in reordering

a job π( j) before the ﬁrst or after the last job of

this block. Let N

and N

be sets of such moves

0 for j ∈ B

and N

0 for j ∈ B

). There-

fore, the neighborhood of the permutation π ∈ Φ

N(π) =

[

j=1

∪

[

j=1

. (5)

As computational experiments show, the neighbor-

hood deﬁned in (5) has a half smaller size than the

neighborhood of all the insert moves.

THE METHODOLOGY OF PARALLEL MEMETIC ALGORITHMS DESIGNING

645

2 MEMETIC ALGORITHM

All operations in a coevolutionary memetic algorithm

(selection, crossover, local optimization and succes-

sion) are executed locally, on some subsets of the cur-

rent population called islands. It is a strongly decen-

tralized model of an evolutionary algorithm. There

are independent evolution processes on each of the

islands, and communication takes place sporadically.

Exchanging individuals between islands secures di-

versity of populations and prevents fast imitating of

an individual with a local minimum as its goal func-

tion. On each island a hybrid algorithm is applied, in

which an evolutionary algorithm is used to determine

the starting solutions for the local search algorithm.

The outline of the standard memetic algorithm is pre-

sented on the Fig. 1.

Algorithm 1. Memetic algorithm

Number of iteration k :=0;

←initial population;

repeat

′

←Selection(P

);

′′

←Crossover(P

′

);

′′

←Mutation(P

′′

);

A ←RandomSubSet(P

′′

);

′′

← P

′′

∪LocalMinimumSet(A);

k+1

←Succession(P

, P

′′

)

k := k + 1;

until

some termination condition is satisﬁed;

Figure 1: Outline of the memetic algorithm.

3 PARALLEL MEMETIC

ALGORITHM

The parallel algorithms based on the island model di-

vide the population into a few subpopulations. Each

of them is assigned to a different processor which per-

forms a sequential memetic algorithm based on its

own subpopulation. The crossover involves only in-

dividuals within the same population. Occasionally,

the processor exchanges individuals through a migra-

tion operator. The main determinants of this model

are: (1) size of the subpopulations, (2) topology of

the connection network, (3) number of individuals to

be exchanged, (4) frequency of exchanging. The is-

land model of parallel memetic algorithm is charac-

terized by a signiﬁcant reduction of the communica-

tion time, compared to the global model (with dis-

tributed computations of the ﬁtness function only).

As shared memory is not required, this model is also

more ﬂexible.

Below, a parallel memetic algorithm is proposed.

The algorithm is based on the island model of par-

allelism (see Bo˙zejko and Wodecki (Bo˙zejko and

Wodecki, 2006)). We have adapted the MSXF (Multi

– Step Crossover Fusion) operator which is used to

extend the process of researching for better solutions

of the problem. Originally, a MSXF has been de-

scribed by Reeves and Yamada (Reeves and Yamada,

1998). Its idea is based on local search, starting from

one of the parent solutions, to ﬁnd a new good so-

lution where the other parent is used as a reference

point. Here we propose to use block properties de-

ﬁned in the Section 1.3.1 to make the search pro-

cess more effective – preventchanges inside the block

(which are unproﬁtable from the ﬁtness function’s

point of view). Such a proceeding is consistent with

an idea of not making unproﬁtable changes between

memes. In this way we design a MSXF+B (MSXF

with blocks) operator.

The neighborhood N (π) of the permutation (in-

dividual) π is deﬁned as a set of new permutations

that can be achieved from π by exactly one adjacent

pairwise exchange operator which exchanges the po-

sitions of two adjacent jobs of a problem’s solution

connected with permutation π. The distance measure

d(π,σ) is deﬁned as a number of adjacent pairwise ex-

changes needed to transform permutation π into per-

mutation σ. Such a measure is known as Kendall’s τ

measure. The outline of the procedure is presented on

the Fig. 2.

Algorithm 2. Multi-Step Crossover

Fusion with Blocks

Let π

, π

be parent solutions. Set x = q = π

;

repeat

Determine blocks in the solution π.

Determine restricted neighborhood N (π)

according to blocks;

For each member y

∈ N (π) calculate d(y

, π

);

Sort y

∈ N (π) in ascending order of d(y

, π

);

repeat

Select y

from N (π) with a probability

inversely proportional to the index i;

Calculate C

sum

);

Accept y

with probability 1,

if C

sum

) ≤ C

sum

(x), and with

probability P

) = exp((C

sum

(x)−

−C

sum

)) / T) otherwise

(T is temperature);

Change the index of y

from i to n and the

indices of y

, k = i+1,. ..,n from k to k−1;

until

is accepted;

x ← y

;

sum

(x) < C

sum

(q)

then

q ← x;

until

some termination condition is satisﬁed;

q is the offspring.

Figure 2: Outline of the Multi-Step Crossover Fusion with

Blocks procedure.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

646

In the implementation proposed here Multi-Step

Crossover Fusion with Blocks (MSXF+B) is an inter-

island (i.e. inter–subpopulation) crossover operator

which constructs a new individual by making use

of the best individuals of different islands connected

with subpopulations on different processors. The con-

dition of termination consisted in exceeding 100 it-

erations by the MSXF+B function. The outline of

the whole parallel memetic algorithm is presented

on the Fig. 3.

Algorithm 3. Parallel memetic algorithm

parfor

j = 1,2,. .. , p { p - #processors }

i ← 0;

← random subpopulation connected

with processor j;

← number of individuals in

j-th subpopulation;

repeat

Selection(P

′

);

Crossover(P

′

′′

);

Mutation(P

′′

);

(k mod R = 0)

then

{every R iteration}

r := random(1, p);

MSXF+B(P

′

(1),P

(1));

end if

;

← P

′′

; i ← i + 1;

there is no improvement of the

average C

sum

then

{Partial restart}

r ← random(1,p);

Remove α = 90 percentage of individuals

in the subpopulation P

;

Replenish P

by random individuals;

end if

;

(k mod S = 0)

then

{Migration}

r ← random(1,p);

Remove β = 20 percentage of individuals

in the subpopulation P

;

Replenish P

by the best individuals

from the subpopulation P

taken from processor r;

end if

;

until

Stop Condition;

end parfor

Figure 3: Outline of the parallel memetic algorithm.

4 COMPUTER SIMULATIONS

The algorithm was implemented in the Ada95

language and ran on the SGI Altix 3700 Bx2

supercomputer installed in Wrocław Center of

Networking and Supercomputing under the Novell

SUSE Linux Enterprise Server operating sys-

tem. Tests were based on 125 instances with

40,50 and 100 jobs taken from the OR-Library

APRD

number of jobs n

1 processor 4 processors

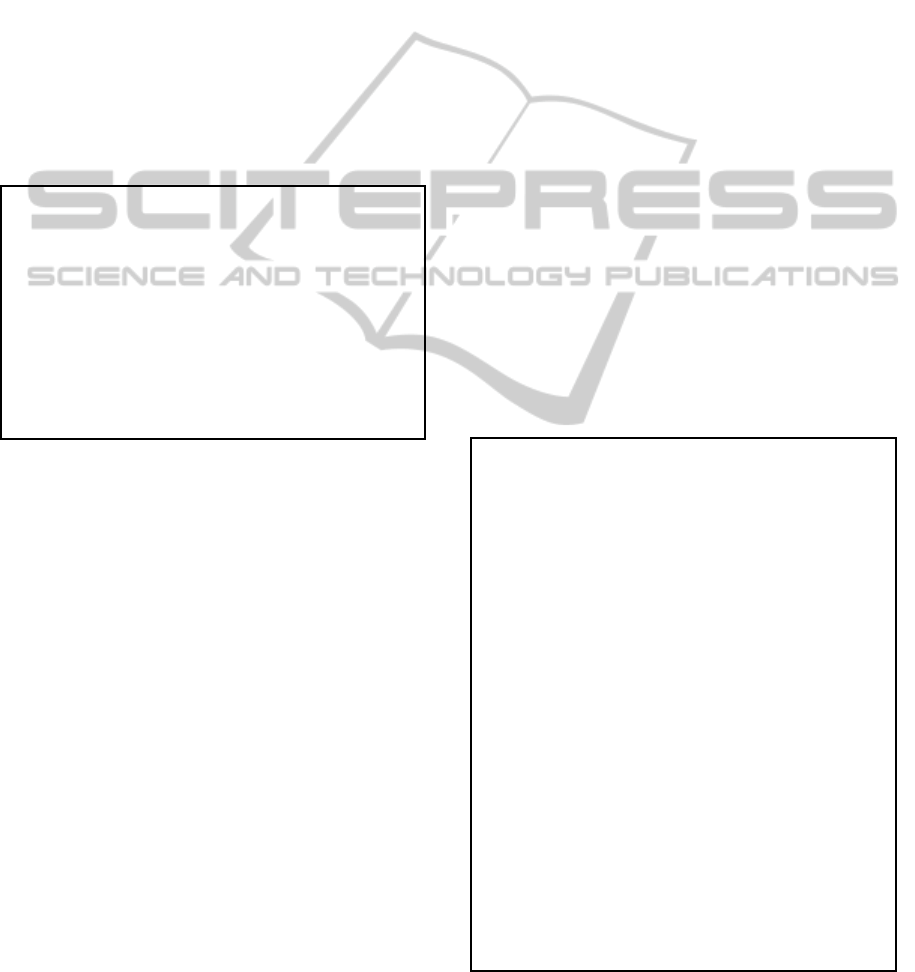
Figure 4: Average percentage relative deviations (APRD)

to the best known solutions for the sequence and parallel

memetic algorithms.

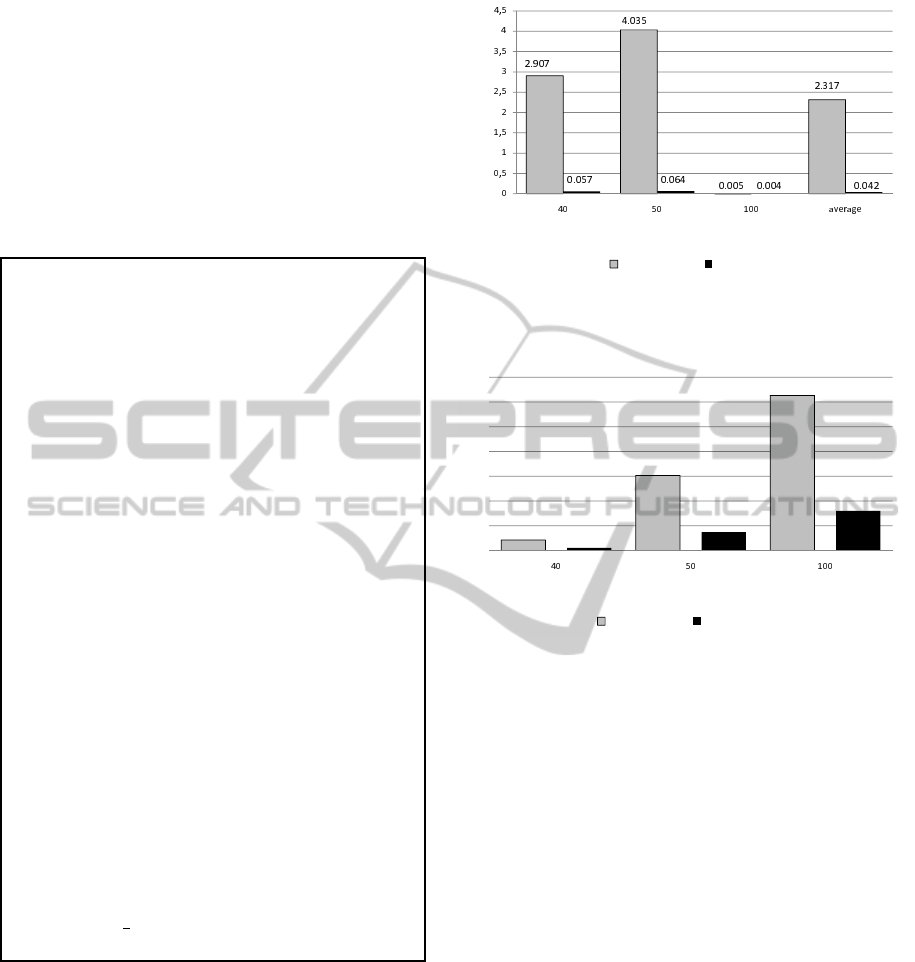
02:03:14

14:34:26

30:04:40

00:32:39

03:35:04

07:40:51

wall time (hours:min:sec)

number of jobs n

1 processor

4 processors

Figure 5: Computing times.

(http://people.brunel.ac.uk/∼mastjjb/jeb/info.html).

The results were compared to the best known, also

taken from OR-Library.

The computational results as well as computing

times are presented on Figures 4 and 5. The num-

ber of iterations was counted as a sum of iterations

on processors, and permanently set to 800. For exam-

ple, 4-processor implementations make 200 iterations

on each of the 4 processors, so we can obtain compa-

rable costs of computations. As we can observe, the

parallel versions of the algorithm achieve much better

results of the average and maximal relative deviation

from the optimal (or the best known) solutions, work-

ing (parallel) in a shorter time. Due to the small cost

of communication the speedup parameter of the par-

allel algorithms is almost linear.

5 REMARKS AND

CONCLUSIONS

The Lamarck evolution theory as well as memetic ap-

proach not only signiﬁcantly extend traditional GA,

but offers more effective approach, too. It is well

THE METHODOLOGY OF PARALLEL MEMETIC ALGORITHMS DESIGNING

647

known, that the classic GA has a week search inten-

siﬁcation phase – genetic operators as well as a mu-

tation mainly diversify the search process. Addition-

ally, in the memetic approach it is possible to make

use of speciﬁc problem properties such as the new

MSXF+B operator with block properties. Embedding

special properties of the problem inside GA is usually

difﬁcult. Further beneﬁts are obtained by using an is-

land model with inter-island operator for the parallel

asynchronous coevolution.

As we observe MA is also able to improve conver-

gence time comparing to GA. Compared to a sequen-

tial algorithm, the parallelization of MA shortens the

computations time and improves quality of obtained

solutions. The proposed methodology of memetic al-

gorithms parallelization can be applied to solve con-

currently all scheduling problems with block proper-

ties, such as ﬂow shop and job shop problems with

makespan criterion, single machine scheduling prob-

lems, etc., for which a solution is represented as a per-

mutation.

ACKNOWLEDGEMENTS

The work was partially supported by the Polish Min-

istry of Science and Higher Education, grant No.

N N514 470439.

REFERENCES

Baker, K. and Scudder, G. (1990). Sequencing with ear-

liness and tardiness penalties: a review. Operations

Research, 38:22–36.

Berger, J. and Barkaoui, M. (2002). A memetic algorithm

for the vehicle routing problem with time windows.

In Proceedings of the 7th International Command

and Control Research and Technology Symposium,

http://www.dodccrp.org/events/7th ICCRTS/Tracks/

pdf/035.pdf.

Bo˙zejko, W. (2010). Parallel path relinking method for

the single machine total weighted tardiness problem

with sequence-dependent setups. Journal of Intelli-

gent Manufacturing, in press, doi: 10.1007/s10845-

009-0253-2.

Bo˙zejko, W., Grabowski, J., and Wodecki, M. (2006).

Block approach tabu search algorithm for single ma-

chine total weighted tardiness problem. Computers &

Industrial Engineering, 50:1–14.

Bo˙zejko, W. and Wodecki, M. (2005). Task realiation’s

optimization with earliness and tardiness penalties in

distributed computation systems. volume 2528 of

Lecture Notes in Artiﬁcial Intelligence, pages 69–75.

Springer.

Bo˙zejko, W. and Wodecki, M. (2006). A new inter-island

genetic operator for optimization problems with block

properties. volume 4029 of Lecture Notes in Artiﬁcial

Intelligence, pages 324–333. Springer.

Bradwell, R. and Brown, K. (1999). Parallel asynchronous

memetic algorithms. In Cantu-Paz, E. and Punch, B.,

editors, Evolutionary Computation, pages 157–159.

Bubak, M. and Sowa, K. (1999). Objectoriented implemen-

tation of parallel genetic algorithms. In Buyya, R.,

editor, High Performance Cluster Computing: Pro-

gramming and Applications, volume 2, pages 331–

349. Prentice Hall.

Crainic, T. and Toulouse, M. (1998). Parallel metaheuris-

tics. In Crainic, T. and Laporte, G., editors, Fleet man-

agement and logistics, pages 205–251. Kluwer.

Crainic, T., Toulouse, M., and Gendreau, M. (1995). Par-

allel asynchronous tabu search in multicommodity lo-

cationallocation with balancing requirements. Annals

of Operations Research, 63:277–299.

Hoogeveen, J. and van de Velde, S. (1996). A branch

and bound algorithm for single-machine earliness-

tardiness scheduling with idle time. INFORMS Jour-

nal on Computing, 8:402–412.

Kliewer, G., Klohs, K., and Tschoke, S. (1999). Parallel

simulated annealing library: User manual. Technical

report, Computer Science Department, University of

Paderborn.

Lenstra, J., Kan, A. R., and Brucker, P. (1977). Complexity

of machine scheduling problems. Annals of Discrete

Mathematics, 1:343–362.

Michalewicz, Z. (1994). Genetic Algorithms + Data Struc-

tures = Evolution Programs. Springer Verlag.

Reeves, C. and Yamada, T. (1998). Genetic algorithms, path

relinking and the ﬂowshop sequencing problem. Evo-

lutionary Computation, 6:45–60.

Smith, W. (1956). Various optimizers for single-stage pro-

duction. Naval Research Logistic Quart, 3:59–66.

Taillard, E. (1991). Robust taboo search for the quadratic

assignment problem. Parallel Computing, 17:443–

455.

Taillard, E. (1994). Parallel taboo search techniques for the

job shop scheduling problem. ORSA Journal on Com-

puting, 6:108–117.

Tang, J., Lim, M., and Ong, Y. (2006). Adaptation for paral-

lel memetic algorithm based on population entropy. In

Proceedings of the 8th Annual Conference on Genetic

and Evolutionary Computation (Seattle, Washington,

USA, July 08 - 12, 2006), GECCO ’06, pages 575–

582. ACM.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

648