PLACEMENT OF HARDWARE TASKS ON FPGA

USING THE BEES ALGORITHM

Bassem Ouni, Ikbel Belaid, Fabrice Muller

University of Nice Sophia-Antipolis, LEAT CNRS, 250 rue Albert Einstein, bat 4, 06560 Valbonne, France

Maher Benjemaa

University of Sfax, National School of Engineers of Sfax, Research Unit ReDCAD, BP 1173-3038 Sfax, Tunisia

Keywords:

Reconﬁgurable zones, Hardware tasks, FPGA, Placement and mapping, Optimization problem, Bees algo-

rithm.

Abstract:

The dynamic and partial reconﬁguration in FPGA with heterogeneous resources is a challenge for the next

years. It allows reconﬁguring a speciﬁc hardware zone in FPGA while maintaining the activity of the remain-

ing circuit’s part. This paper introduces a new approach about how to solve the problem of placement of the

hardware tasks on the recent reconﬁgurable technology using the honey Bees Algorithm. This approach aims

at performing a good placement by maximizing the efﬁciency of the used resources and reducing the task’s

reconﬁguration overheads. Experimental results show that the proposed method can perform a good place-

ment of hardware tasks on the device by optimizing signiﬁcantly the parameters of the cost function in terms

of resources and execution time.

1 INTRODUCTION

The reconﬁgurable hardware technologies are charac-

terized by many heterogeneous resources and multi-

tasking. Hence, managing the hardware tasks and re-

sources is strongly required. The placement of hard-

ware tasks on FPGA consists of two steps: the ﬁrst

step is the partitioning, which manages the empty

space in the technology and identiﬁes the potential

sites enabling execution of hardware tasks. The sec-

ond step is the ﬁtting, which selects the feasible place-

ment solution.

In (Bazargan et al., 2000), two methods of place-

ment are introduced: the ﬁrst one called Keeping All

Maximal Empty Rectangles (KAMER) searches all

the Maximal Empty Rectangles (MER) after plac-

ing each task. Bazargan deﬁnes the MERs as the

empty rectangles which are not contained in another

empty rectangle and which are not necessarily dis-

joined. The second method denoted Keeping Non-

overlapping Empty Rectangles keeps all the non-

overlapping holes and is evoked after each split or

merge operation.The work in (Ahmadinia et al., 2004)

introduces a new method of on-line placement by

managing the occupied space instead of free space

due to the big size of the empty rectangles and the

hardness of managing the free space.

The authors in (Marconi et al., 2008) extend the

Bazargan’s placement using an Intelligent Merging

(IM) algorithm. IM combines three techniques of

managing free resources: Merging only if Needed,

Partially Merging and Direct Combine. IM acceler-

ates Bazargan’s method by three times and improves

the placement quality by increasing the rate of ac-

cepted tasks.

A new approach of placement is introduced in

(Handa and Vemuri, 2004) : the method of staircase.

It handles the free space during the ﬁrst step of the

online placement. It tries to improve the KAMER

method especially for tasks rejection.

Dissimilar to the other methods, we proposed in

recent works an approach which takes into account

the hardware tasks heterogeneity and it is applicable

in the high complex applications. This method of off-

line placement classiﬁes the hardware tasks into many

classes based on their resources; these classes are

called RZ types (Reconﬁgurable Zones). The phys-

ical representations of the RZs are RPBs (Reconﬁg-

urable Physical Blocs). These RPBs are 2D rectangu-

lar blocs representing the possible physical locations

498

Ouni B., Belaid I., Muller F. and Benjemaa M..

PLACEMENT OF HARDWARE TASKS ON FPGA USING THE BEES ALGORITHM.

DOI: 10.5220/0003361804980505

In Proceedings of the 1st International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2011), pages

498-505

ISBN: 978-989-8425-48-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

of RZs in the device. As depicted by Figure 1, RZs

and RPBs are modeled by blocs of heterogeneous re-

sources called Reconﬁgurable Blocs (RB) to obtain

models called RB-models.

Under the French research program FOSFOR

project

(FOSFOR, 2010), we aim at seeking a good

solution of the placement problem using the Bees Al-

gorithm. This good solution tries to enhance the re-

sources efﬁciency and the execution time and it is

not necessary that it ensures the minimum of the cost

function. The paper is structured as follows: in sec-

Figure 1: Example of RPBs of RZ.

tion 2 an overview of the problem of hardware tasks’

placement on the device is presented. Inside section

3, the Bees Algorithm is introduced. Section 4 deals

with our proposed method to solve this problem based

on the Bees Algorithm. Then, section 5 shows the ex-

perimental results and ﬁnally in section 6 conclusions

and future works are drawn.

2 THE PLACEMENT PROBLEM

The placement problem consists in placing the RZs

on the possible RPBs and mapping the tasks on these

RZs. This problem is a combinatory optimization

problem under constraints. It is characterized by an

explosive space of admissible solutions. The place-

ment/mapping problem is deﬁned by the couple (S,

F), where S represents the set of the admissible so-

lutions and F(S ⇒ R, R is a set of reals) depicts

the objective function of minimization. The resolu-

tion of the problem consists in searching the solu-

tion s

∗

included in S where f (s

∗

) ≤ f (s) for each s

in S. As all the problems of optimization under con-

straints, the problem of placement/mapping is deﬁned

by the quadruplet (X,D,C,F), where X = {X1,X2}

FOSFOR (Flexible Operating System For Reconﬁg-

urable platform) is French program aiming at designing a

real time operating system distributed on hardware and soft-

ware execution units which offers required ﬂexibility to ap-

plication tasks through the run-time reconﬁguration and ho-

mogeneous HW/SW OS services.

and D = {D1, D2}. X1 contains the ﬁrst set of vari-

ables which consists of RPB coordinates, their widths

and their heights, X2 contains the occupation rates

of each task on the placed RZs, D1 and D2 repre-

sent respectively the ﬁnite domains of possible val-

ues of variables of X1 and X2. Hence, a potential

solution for the problem consists in assigning each

variable from X1 and X2 to a value from D1 and

D2. C is a set of constraints which checks whether

the combination of values is compatible with the vari-

ables. F is the minimization objective function which

expresses the optimization criteria and enables the

research of the optimal solution from the admissi-

ble ones. Consequently, we have associated to the

placement/mapping problem the following non-linear

mathematical model.

2.1 Constants

The constants are:

NT : number of tasks ; NZ: number of RZs.

NPB: number of RPBs ; NP: number of types of RBs.

Device width: width of the device.

Device height: height of the device.

Device RB[lines][columns] of RBs: RB−model of the

device.

RB[NP]of RBs: RB − model of the RZ

RPB

RB[NP]of RBs: RB − model of the RPB

RBType[NP]: the NP types of RBs.

: cost of the correspondent RB

: the WCET

of task T

; P

: the period of task T

Con f ig

: reconﬁguration overhead of a task T

T hreshold

: the lower threshold of occupation rate for

task T

in RZs.

2.2 Variables (X)

X1 = {(X

),(X

),W

,1 ≤ j ≤ NZ}.

X2 = {δ

,1 ≤ j ≤ NZ,1 ≤ i ≤ NT }.

Where:

): coordinates of the highest left vertex of

the RPB for RZ

): coordinates of the lowest right vertex of

the RPB for RZ

: width of the RPB for RZ

; H

: height of the

RPB for RZ

:occupation rate of RZ

by T

WCET (Worst-case execution time) is the maximum

duration the task could take to run on a speciﬁc hardware

platform.

PLACEMENT OF HARDWARE TASKS ON FPGA USING THE BEES ALGORITHM

499

2.3 Domains (D)

D1 = {d

,dw,dh are domains of naturals:

= d

= dw = [0,Device width],d

= d

= dh =

[0,Device height]}.

D2 = {d

is a domain of naturals, 1 ≤ j ≤ NZ,

1 ≤ i ≤ NT : d

= {0} or d

= {100} or d

[T hreshold

,100 − T hreshold

]}.

2.4 Constraints (C)

2.4.1 Overlapping Constraint (CP1)

This analytic expression (1) should be respected to

avoid the overlapping between the RPBs.

∀p,q, p ̸= q,et∀RZ

,RZ

< X

orY

+ H

< Y

orY

+ H

< Y

(1)

2.4.2 Heterogeneity Constraint (CP2)

This constraint (2) checks, before the placement of RZ

on RPB, the existence of the type and the number of

RBs required by RZ in this RPB.

∀RZ

∑

<n<Y

<m<X

∑

device[m][n]=RBT ype[k]

1 (2)

2.4.3 Total Execution for Tasks Constraint

(CM1)

This expression (3) veriﬁes whether the totality of the

task is well executed.

∀T

∑

1≤ j≤NZ

j,i

≤ 100% (3)

2.4.4 Overload of RZs Constraint (CM2)

The following constraint (4) evades the RZ overload.

∀RZ

∑

i∈{Tasks idwithinRZ

}

j,i

×C

+Con f ig

j,i

≤ Load Scheduling (4)

Where Load Scheduling represents the percentage

which should not be exceeded to avoid RZ overload.

It depends on the scheduling policy. In our case,

Load Scheduling = 100% because the tasks are in-

dependent and the scheduling policy is EDF.

2.5 Minimization Objective Function

(F) is the cost function of the placement and mapping

problem. We target to minimize this function (5).

F(X ) = Coe f f g1 × EFF(X) +

Coe f f g2 × MAP(X ) (5)

EFF. This parameter evaluates the resources efﬁ-

ciency of the current placement of RZs on the appro-

priate RPBs.

MAP. This parameter evaluates the optimality of

the mapping of tasks on the RZs. If the mapping of a

task in RZ is impossible, the value of MAP returns -1.

The two previous parameters are weighted in the

objective function F by the coefﬁcients Coeffg1 and

Coeffg2. Let’s consider RPB

the RPB where the RZ

is placed within the current solution X. The following

equations (6) and (7) represent these parameters.

EFF(X ) =

∑

1≤ j≤NZ

∑

1≤k≤NP

×(RPB

RB[k] − RZ

RB[k]) (6)

MAP(X) =

∑

1≤m≤3

Coe f f p

× MAP

(X) (7)

Where Coe f f p

represents the coefﬁcient of each

parameter MAP

Lets consider Load RZ

the load of RZ

for each task

placed in this RZ, it is depicted by this equation (8).

Load RZ

∑

p∈{T asks idwithinRZ

}

i,p

×C

+Con f ig

i,p

(8)

As showed in the following expression (9), the ﬁrst

expression of MAP

evaluates whether the RZ is

fully exploited. The second one checks whether the

loads of placed RZs are balanced, it means checking

whether the loads of all RZs are near to the needed

average: Aver age Load.

MAP

(X) =

∑

1≤ j≤NZ

(100% − Load RZ

) +

((Load RZ

− Average Load)

)/NZ (9)

Where Average Load =

∑

1≤ j≤NZ

Load RZ

/NZ

MAP

computes the sum of the reconﬁguration times.

It evaluates whether the tasks are much split on the

RZs in order to avoid overheads (reconﬁguration and

context switch). The reconﬁguration overhead de-

pends on RZs and tasks. Thus, MAP

favorites map-

ping tasks with high occupation rates in the RZs assur-

ing the best efﬁciency of resources. MAP

is written

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

500

as follows (10):

MAP

(X) =

∑

1≤i≤NZ

∑

1≤p≤NT

i,p

̸=0

Con f ig

i,p

× npr

i,p

(10)

Where npr

represents the maximal number of

preemptions of the task T

mapped on RZ

MAP

improves the execution time of each task and

the quality of services (QoS). It is also computed with

the following assumption: the task T

that is mapped

in RZ

could be preempted only if δ

j,i

% of this task

is executed.

MAP

calculates the cost of the used RZs during the

placement of all the tasks on the device. The costs of

the resources are determined taking into account the

information in (Xilinx, 2009). The expression (11)

depicts MAP

MAP

(X) =

∑

1≤k≤NP

∑

load RZ

̸=0

1≤i≤NZ

× Z

i,k

(11)

Where Z

i,k

is the number of RB

in RZ

In recent works, we demonstrated that the place-

ment/mapping problem is NP hard so that we will

solve it using a heuristic method: the Bees algorithm.

3 THE BEES ALGORITHM

The Bees algorithm is inspired by the food foraging

behavior of the honey bees (Pham et al., 2006; Pham

et al., 2007b) and could be regarded as an intelligent

optimization tool. This algorithm is used to solve the

multi-objective problems and it is able to locate good

solutions efﬁciently (Pham and Ghanbarzadeh, 2007;

Pham et al., 2007a). The following code is the pseudo

code of the Bees Algorithm:

1. Initialize the population with random solutions

(Placing (n) bees randomly in the search space).

2. Evaluate the ﬁtness of the visited sites (patches of

ﬂowers).

While (stopping criterion is not met)

3. Select (m) best sites having the highest ﬁtness

and also choose the (e) elite sites among these best

patches.

4. Recruit a number (nsp) bees for (m) selected sites

and a number (nep) bees for (e) elite sites and evalu-

ate ﬁtness (wherensp < nep).

5. Select the ﬁttest bee from each patch.

6. Assign the (n − m) remaining bees to search ran-

domly and evaluate their ﬁtness.

End While.

We propose to adapt the Bees Algorithm with our

context of placement and mapping of the tasks so that

we can exploit the effectiveness of this algorithm to

solve the placement problem.

4 THE PROPOSED METHOD

The objective of the proposed method is minimizing

the cost function to obtain a good placement and map-

ping of hardware tasks on the device. The entries of

this method are the RZs, which are generated from the

hardware tasks, and the RPBs. The outputs are hard-

ware tasks placed on the technology while optimizing

the various parameters of the objective function. In

other words, the solution of the placement/mapping

problem is the hardware tasks mapped on RZs which

are placed in RPBs. Accordingly, we consider a bee as

a combination of RZs which already contain the hard-

ware tasks. This combination is depicted by a vector

of RZs: RZV . We also consider a patch of ﬂowers

as a combination of RPBs which is represented by a

vector of RPBs: RPBV . As illustrated by Figure 2,

the set {P

,k ∈ [1,nprm]} represents the preemption

points of the task T

, T

is the k−th execution section

of this task and nprm is the number of preemptions of

Figure 2: Preemption points and execution sections of T

We repeat these next steps Nitermapping times.

4.1 Step 1: Generate Arbitrarily the

Occupation Rates Matrix

The ﬁrst step consists in calculating the matrix P

which contains the occupation rates of the tasks in

the RZs. Like the random choice of the scout bees

from the colony to explore the ﬂowers, this matrix is

randomly generated so that the RZVs are chosen ar-

bitrarily. Every line of this matrix should respect the

constraint (CM1) and every column should also re-

spect the constraint (CM2). The elements of this ma-

trix (P = p

,1 ≤ i ≤ NT,1 ≤ j ≤ NZ) are vectors

of the hardware tasks execution sections. Each exe-

cution section of a task is assigned randomly to a pos-

sible RZ containing enough resources to execute this

task. It is not necessary that the execution sections of

a task are assigned to all the possible RZs thus we can

ﬁnd an RZ where the mapping of some tasks is pos-

sible but does not contain any execution section. In

this case, p

= (0). Also, if the mapping of a task T

in RZ

is impossible, p

= (0). Figure 3 shows the

structure of this matrix.

Where k, p and q are naturals in [1,nprm].

The next steps (from 2 to 7) are repeated Nitr

times.

PLACEMENT OF HARDWARE TASKS ON FPGA USING THE BEES ALGORITHM

501

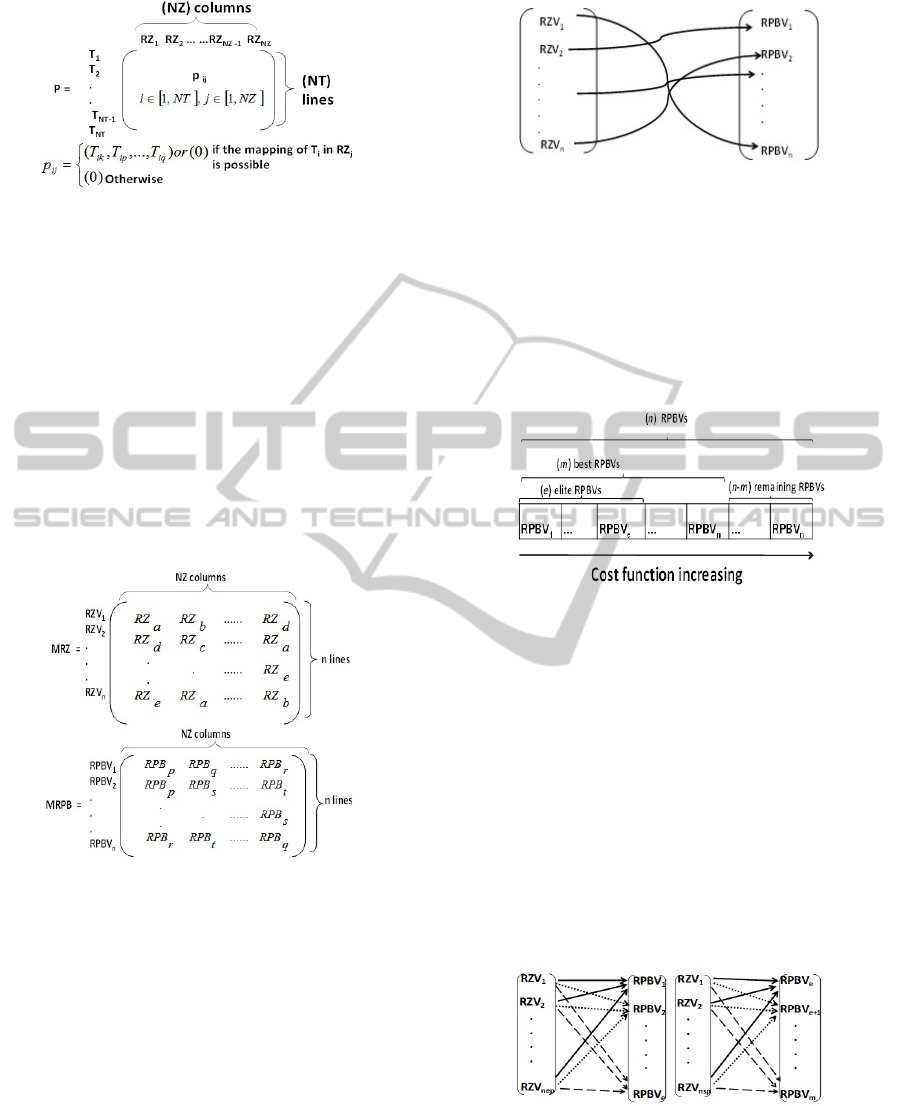
Figure 3: Occupation rates matrix.

4.2 Step 2: Random Construction of the

Matrix of RZs and RPBs

In this step, we target to prepare the n RZVs and n

RPBVs. As showed in Figure 4, we generate the ma-

trices MRZ and MRPB containing respectively n dif-

ferent RZVs and n different RPBVs. MRPB takes into

account the overlapping constraint (CP1): A combi-

nation of RPBs depicted by one line of MRPB must

not contain overlapped RPBs. The two matrices have

the same dimension: n lines and NZ columns.

In Figure 4, a, b, c, d and e are naturals in [1,NZ] and

p, q, r, s and t are naturals in [1,NPB].

Figure 4: The matrices of the RZs and RPBs.

4.3 Step 3: Place Randomly the RZs on

the RPBs

As depicted in Figure 5, this step, by analogy to the

random bees’ exploration of the ﬂowers patches, in-

volves placing randomly the RZVs on the RPBVs.

During the placement, we must take into account the

possibility of placement by checking that there are

enough resources in RPB to execute the RZ and the

fact that an RPB can contain only one RZ.

Figure 5: Random placement of the RZs on the RPBs.

4.4 Step 4: Sort the RPBVs According

to the Cost Function

This step begins by sorting RPBVs in an ascending

order according to the cost function. Then, we select

the m best RPBVs among which we choose the e elite

RPBVs. Figure 6 illustrates the RPBVs sort.

Figure 6: The RPBVs sort.

4.5 Step 5: Generate the Matrices of the

Elite and Best RPBVs

Like in the colony of bees which assigns a big num-

ber nep of bees to the e elite patches, we place nep

RZVs on each elite RPBV from the e elite RPBVs

and then determine the RZV ensuring the minimum

cost function for each RPBV. Similarly, on each best

RPBV from the (m-e) best RPBVs, we place nsp RZVs

(nsp < nep) and we also determine the RZV ensuring

the minimum cost function for each RPBV. Figure 7

shows these placements.

According to these placements, we construct the

Figure 7: Placement of (nep) RZVs on the (e) elite RPBVs

and (nsp) RZVs on the (m-e) best RPBVs.

matrices EliteFitnessMatrix and SelectedFitnessMa-

trix which contain respectively the cost functions of

the elite and best RPBVs. Figure 8 and Figure 9 indi-

cate these matrices.

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

502

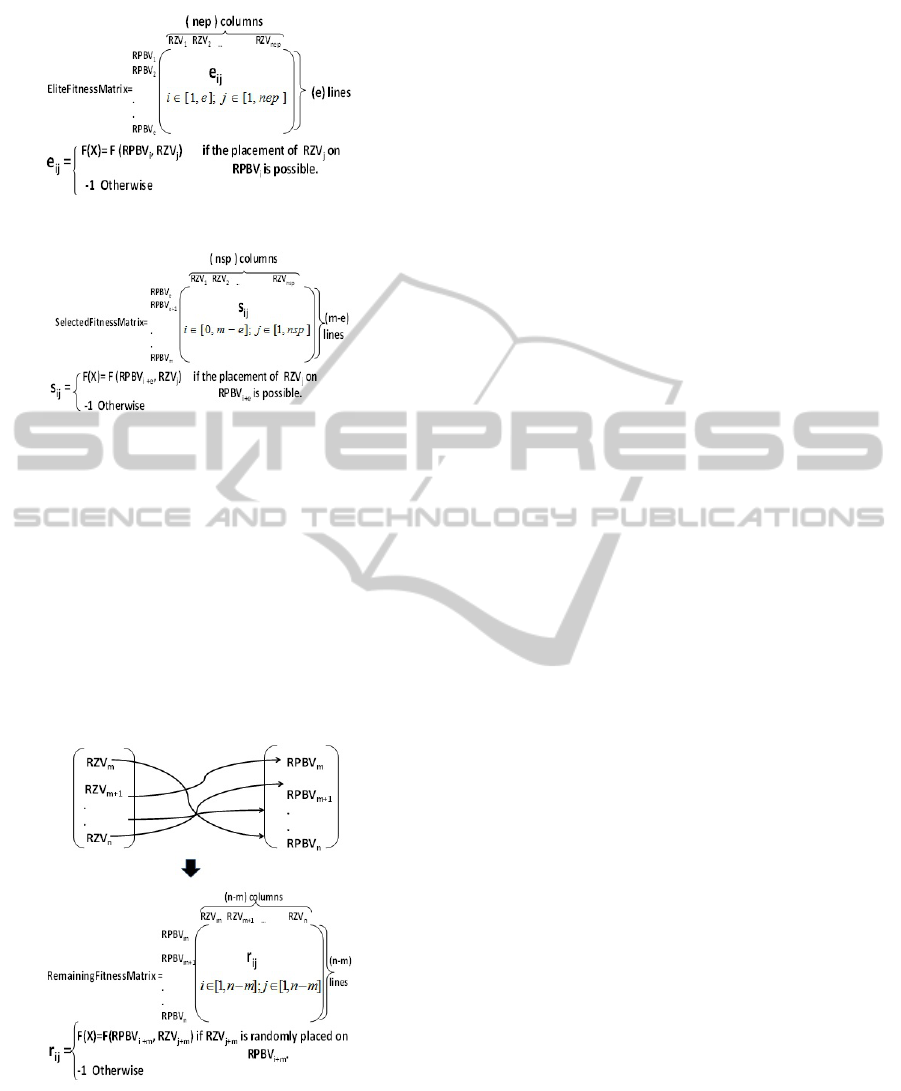
Figure 8: The matrix of the elite RPBVs.

Figure 9: The matrix of the best RPBVs.

4.6 Step 6: Generate the Matrices of the

Remaining RPBVs

By analogy to the Bees Algorithm which assigns the

(n − m) remaining bees to search randomly the nectar

in the (n − m) remaining patches, we place arbitrarily

the (n − m) remaining RZVs on the (n − m) remain-

ing RPBVs. Then, as showed in Figure 10, we gen-

erate the matrix RemainingFitnessMatrix which con-

tains the cost functions resulting from these place-

ments.

Figure 10: The matrix of the remaining RPBVs.

4.7 Step 7: Generate the Matrices of the

Elite and Best RPBVs

After each iteration from the Nitr ones, we select

the couple (RZV

,RPBV

) ensuring the minimum of

the cost function e

. The value of e

is exactly the

minimum of the three matrices: EliteFitnessMatrix,

SelectedFitnessMatrix and RemainingFitnessMatrix.

RZV

and RPBV

are respectively the correspondents

RZV and RPBV.

We repeat the previous steps (from step 2 to step

7) Nitr times and we keep the results of each itera-

tion (the minimum of the cost function e

and the

couple (RZV

,RPBV

)) in a three dimensional ta-

ble: TBEE. Therefore, TBEE contains Nitr elements.

Then, we choose the minimum of the cost function

from this table e

min

and the correspondent couple

(RZV

min

,RPBV

min

). We also repeat the previous steps

(from step 1 to step 7) Nitrmapping times and we

keep, after each iteration, the results obtained next to

the Nitr iterations: e

min

and the correspondent cou-

ple (RZV

min

,RPBV

min

) in a three dimensional table:

TGLOBAL. Thus, the size of TGLOBAL is Nitrmap-

ping. Then, we choose the ﬁnal solution which is the

minimum of the cost function in TGLOBAL: e

opt

and

the correspondent couple (RZV

opt

,RPBV

opt

In our approach, the tasks with the same type are

grouped in RZs. Thus, placing an RZ means plac-

ing a set of tasks at once unlike the off-line place-

ment method in (Danne and Stuehmeier, 2005) which

handles tasks independently from each other leading

to the increase of the tasks’ rejection. In addition, if

we have a big number of tasks, the complexity of the

problem in the proposed method will be small com-

pared to Danne and Stuehmeier method as the num-

ber of RZs to place is fewer than that of tasks. Also,

we take into consideration the preemptions of tasks

and the overheads which is not the case in (Danne

and Stuehmeier, 2005). Besides, we integrate the

whole problem in a single heuristic while the method

in (Danne and Stuehmeier, 2005) uses three heuristics

to validate only its ﬁrst step of placement.

5 EXPERIMENTAL RESULTS

To illustrate the proposed method, we have imple-

mented an application composed of hardware tasks

that are frequently used in the recent embedded sys-

tems performing video and audio applications. This

application is characterized by hardware tasks of var-

ied sizes and of heterogeneous resources. The hard-

ware tasks are centralized around the microcontroller

(T48) which conﬁgures these tasks and synchronizes

the data ﬂow. During the design of this application,

we have synthesized the resources of each hardware

task by the Xilinx tool ISE 11.3 and we have de-

termined the conﬁguration overheads of the obtained

RZs by performing the partial reconﬁguration ﬂow by

PLACEMENT OF HARDWARE TASKS ON FPGA USING THE BEES ALGORITHM

503

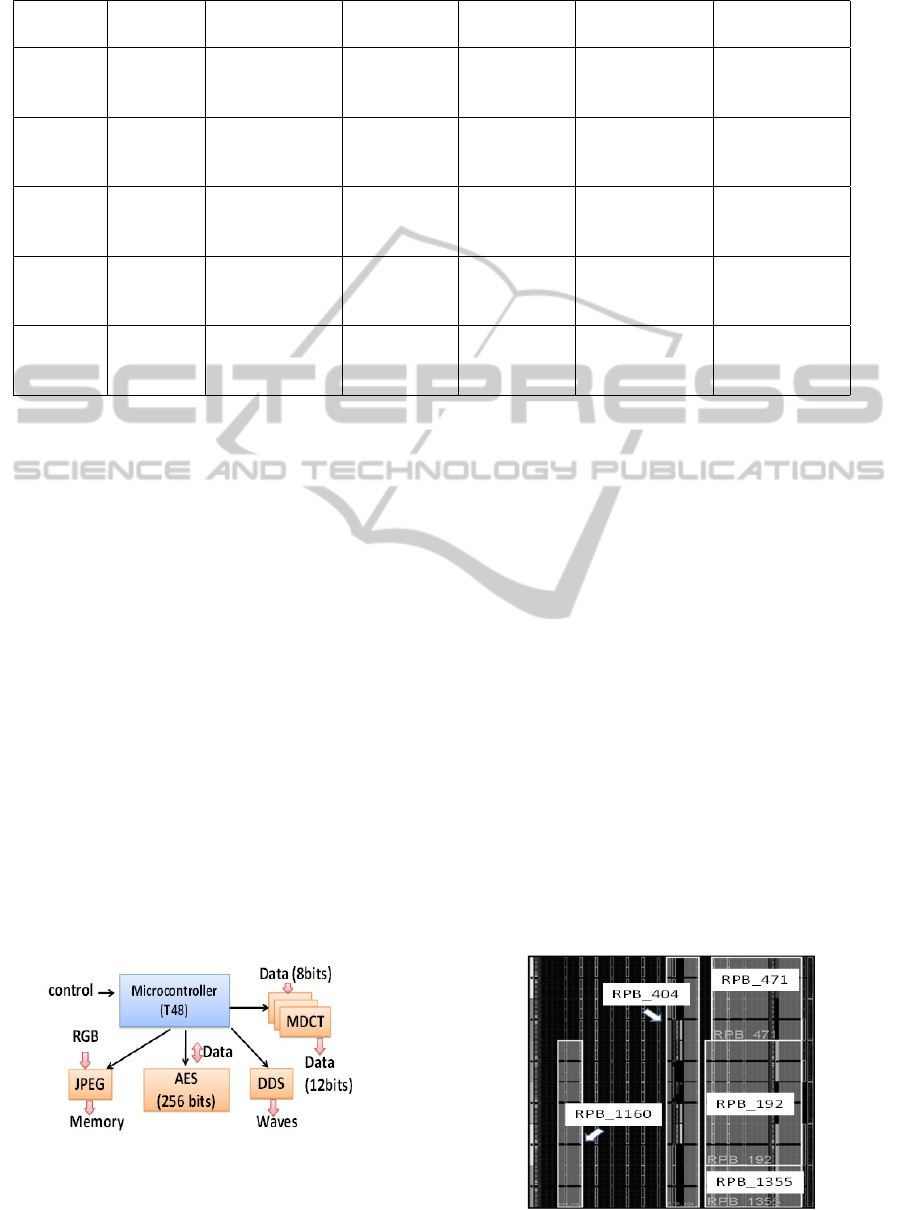
Table 1: Hardware tasks features.

Modules Instances RBs WCET (µs) Period (µs) Conﬁguration

overhead (µs)

Pre-emption

points (µs)

MDCT {T

} {2RB

12RB

3RB

, 0RB

}

40552 416666 1856 10000,

20000, 30000

AES {T

} {4RB

7RB

, 1RB

1RB

}

51540 100000 2185 30000, 40000

DDS {T

} {0RB

1RB

, 1RB

1RB

}

5000 12000 432 1000, 2000,

4000

T48 {T

} {5RB

4RB

, 0RB

0RB

}

20000 50000 605 5000, 10000,

15000

JPEG {T

} {8RB

12RB

0RB

, 2RB

}

350000 416666 2421 200000,

300000

means of Xilinx tool Planahead 11.3 and by taking

into account I/O routing.

Figure 11 indicates the hardware tasks compos-

ing the application and the microcontroller T48 which

manages these tasks. The AES (Advanced Encryp-

tion Standard) task encrypts blocks of 20 Kbytes us-

ing a key of 256 bits. The MDCT module calculates

the Modiﬁed Discrete Cosine Transform. JPEG task

provides a hardware compression of 24 frames per

second. The DDS (Direct Digital Synthesizer) mod-

ule generates sinusoidal and programmable waves

with adjustable frequency and phase. The character-

istics of hardware tasks and their instances are pre-

sented in Table 1. These RBs are determined taking

into account the reconﬁguration granularity and the

resources area in Virtex 5 technology (Xilinx, 2009).

It contains 4 main types of resources CLBL, CLBM,

BRAM and DSP. Therefore, RB

is 20 CLBL s, RB

is 20 CLBMs, RB

is 4 BRAMs and RB

is 8 DSPs.

The preemption points are generated arbitrarily and

based on the granularity and the WCET of the hard-

ware tasks. For all the tasks, we consider that the ﬁrst

preemption point is equal to 0 µs.

Figure 11: Hardware tasks of the application.

The parameters of the Bees Algorithm cho-

sen to solve this problem are the following:

NiterMapping = 5, Nitr = 2, n = 6, m = 4, e = 2,

nep = 4 and nsp = 2.

Table 2 shows the RZs (Virtex 5 SX50T) and the

number of possible RPBs. The good solution, re-

sulting from the proposed method, is showed in Ta-

ble 3. It indicates the different execution sections of

the tasks mapped on the RZs which are placed on the

RPBs. This solution optimizes the parameters of the

placement/mapping problem by minimizing the cost

function (F). To illustrate the proposed method, we

vary the parameter NiterMapping which represents

the number of repetitions of the Bees Algorithm. We

note that the more we repeat the Bees Algorithm, the

more the cost function reduces.

Figure 12 depicts the ﬂoorplanning of RPBs on the

technology Virtex 5.

The RPBs are so limited on the device so that we

optimize the exploitation of resources and we avoid

the resources waste. Thus, we preserve sufﬁcient

space for the static design. This optimization in use

of resources minimizes the reconﬁguration overhead

of FPGA.

Figure 12: Floorplanning of RPBs on Virtex 5 SX50T.

PECCS 2011 - International Conference on Pervasive and Embedded Computing and Communication Systems

504

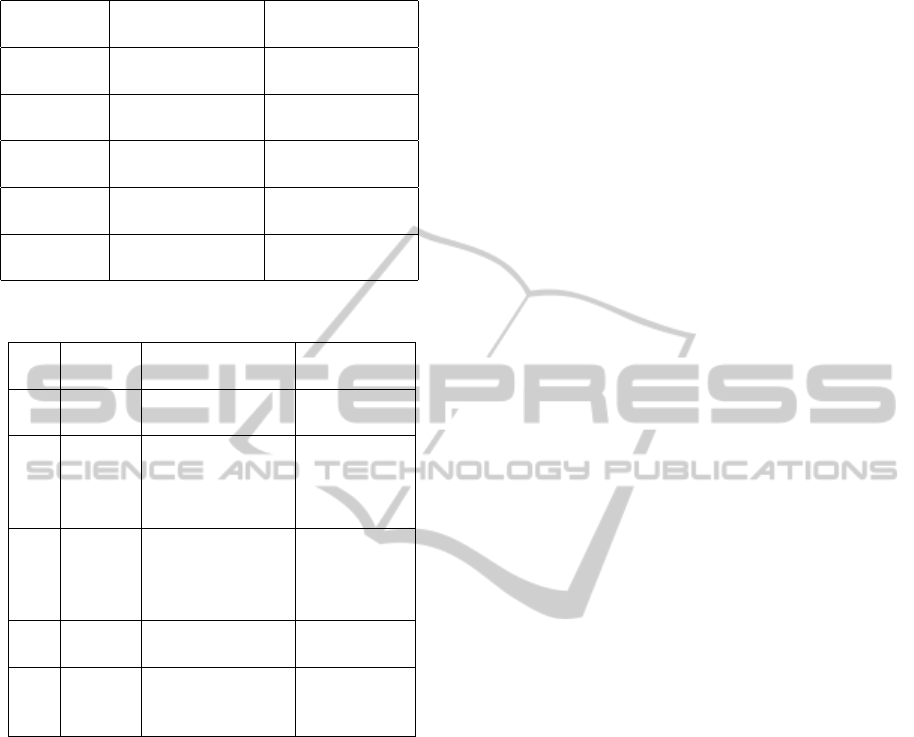
Table 2: The number of RZs and possible RPBs.

RZs RBs Number of pos-

sible RPBs

{2RB

,12RB

3RB

,0RB

}

415

{4RB

,7RB

1RB

,1RB

}

534

{0RB

,1RB

1RB

,1RB

}

294

{5RB

,4RB

0RB

,0RB

}

617

{8RB

,12RB

0RB

,2RB

}

410

Table 3: Results of the Bees Algorithm.

RZ RPB Tasks Occupation

rate of RZ

RPB

192

7,1

7,2

7,3

(100%o f T

)

83,1776%

RPB

404

1,1

1,2

1,3

1,4

(100%o f T

)

2,1

2,2

2,3

2,4

(100%o f T

)

19,306%

RPB

471

3,1

3,2

3,3

(100%o f T

)

4,1

4,2

4,4

(83%o f T

)

85,8802%

RPB

1355

6,1

6,2

6,3

6,4

(100%o f T

)

40,0484%

RPB

1160

4,3

(17%o f T

)

5,1

5,2

5,3

5,4

(100%o f T

)

48,5133%

6 CONCLUSIONS

In this paper, we propose a heuristic method to solve

the problem of hardware tasks placement on FPGA

technology (Virtex 5) based on the Bees Algorithm.

We tried to optimize the parameters of this con-

strained optimization problem so that we reduce the

cost function. We also avoid the tasks rejection as we

pack tasks on RZs and we employ the dynamic par-

tial reconﬁguration. Our experimental results show

the efﬁciency of this method in terms of resources and

reconﬁguration overhead.

We plan in a future work to propose another method

and to compare it with the Bees Algorithm. Also, we

will exploit the results of this off-line placement to

achieve an on-line scheduling of the tasks taking into

account the inter-task communication and real time

constraints.

ACKNOWLEDGEMENTS

The authors would like to thank the national agency

of research in France and the world-ranking Secured

Communicating Solutions (SCS) cluster that sponsor

our research project FOSFOR. This work was sup-

ported by AIMMS technical support and Xilinx tools.

REFERENCES

Ahmadinia, A., Bobda, C., Bednara, M., and Teich, J.

(2004). A new approach for on-line placement on re-

conﬁgurable devices. International Parallel and Dis-

tributed Processing Symposium (IPDPS), Santa Fe,

NM, U.S.A., page 134.

Bazargan, K., Kastner, R., and Sarrafzadeh, M. (2000). Fast

template placement for reconﬁgurable computing sys-

tems. IEEE Design and Test, Special Issue on Recon-

ﬁgurable Computing, pages 68–83.

Danne, K. and Stuehmeier, S. (2005). Off-line placement

of tasks onto reconﬁgurable hardware considering ge-

ometrical task variants. IFIP conference.

FOSFOR (2010). Fosfor project, 2010.

http://www.polytech.unice.fr/ fmuller/fosfor.

Handa, M. and Vemuri, R. (2004). An efﬁcient algorithm

for ﬁnding empty space for online fpga placement.

Design Automation Conference (DAC), San Diego,

California, USA, pages 960–965.

Marconi, T., Lu, Y., Bertels, K., and Gaydadjiev, G. (2008).

Task placement algorithm for partial reconﬁgurable

systems. Design Automation Test Europe (DATE),

Munich, Germany, pages 1346–1351.

Pham, D. and Ghanbarzadeh, A. (2007). Multi-objective

optimisation using the bees algorithm. Proceedings of

IPROMS, Cardiff, UK.

Pham, D., Ghanbarzadeh, A., Koc, E., Otri, S., Rahim, S.,

and Zaidi, M. (2006). The bees algorithm - a novel

tool for complex optimisation problems. Proceedings

of IPROMS, Cardiff, UK.

Pham, D., Haj Darwish, A., Eldukhri, E., and Otri, S.

(2007a). Using the bees algorithm to tune a fuzzy

logic controller for a robot gymnast. Proceedings of

IPROMS, Cardiff, UK.

Pham, D. T., Aﬁfy, A., and Koc, E. (2007b). Manufactur-

ing cell formation using the bees algorithm. IPROMS

conference.

Xilinx (2009). Xilinx, 2009. virtex-5 fpga conﬁguration

user guide. Technical report.

PLACEMENT OF HARDWARE TASKS ON FPGA USING THE BEES ALGORITHM

505