GENERATING MULTIDIMENSIONAL RESPONSE SURFACES
FROM PROCESS DATA
Finding Optimal Set Points for Machine Control
Wolfgang Mergenthaler, Jens Feller, Bernhard Mauersberg
FCE Frankfurt Consulting Engineers GmbH, Altmünsterstrasse 2D, D-65439 Flörsheim, Germany
Roger Chevalier
Electricité de France, R&D, 6, Quai Watier, F-78401 Chatou Cedex, France
Keywords: Multidimensional Response Surfaces, Nonlinear Optimization, Dynamic Programming, Gaussian Shapes,
Adaptive Control, Statistical Learning.
Abstract: Technical processes, notably in the power transforming industries, generate a wealth of process data,
commonly organized in a file with M records and 1 + n + m fields, i.e. a time stamp, followed by n
independent and m dependent variables, summarized in the vectors x and y, respectively. Regardless of the
availability of physical models it is interesting and often necessary to generate functional relationships
between x and y from process data. The most prominent purpose is the optimization of certain performance
indices under given constraints. This paper describes response surface estimation using Gaussian shapes
along with finding optimal points on the surfaces to be used in machine control. The practical impact lies in
the usability of this technique to increase machine efficiency on a broad industrial scale with its applications
towards energy efficiency and climate protection.
1 INTRODUCTION
Technical processes, notably in the power
transforming domain, continuously produce a large
series of data at a given sampling rate determined by
a time interval
0>Δt
. At any particular time
assume there are M records given, organized into a
time stamp, n independent (or state) variables and m
dependent (or response) variables. These fields are
summarized in the n- and m-dimensional vectors x
and y. For instance, when monitoring power
generating systems such gas turbines, there are up to
1200 signals monitored simultaneously, comprising
ambient conditions, pressures, temperatures, mass
flows, guide vane angles, vibration amplitudes in
various channels etc. Not all of those, of course, find
their place in physical models, which are usually
dominated by thermodynamics, but reveal a lot of
information about the system, worthwhile to be
exploited.
Therefore, whether or not there is a physical
model expressing y – or, rather, its expected value –
in terms of x, it is always useful and sometimes
necessary to estimate the functional dependence,
using process data only.
With such a functional dependence established, a
multitude of applications in system control, process
optimization and experimental design come into
view.
It is the goal of this paper to show that there is a
class of functions, called linear combinations of
Gaussian shapes below, which allow to approximate
an arbitrary cloud of points precisely and can be
differentiated continuously infinitely often. This
property is conducive to many tasks in mathematical
optimization and machine control, as shown below.
2 MODEL
Let this functional relationship be described by a
function y, where
ε
+
=
)(xfy
(1)
mn
RRf →:
(2)
and
ε
, for the sake of simplicity, is assumed to be a
397
Mergenthaler W., Feller J., Mauersberg B. and Chevalier R..
GENERATING MULTIDIMENSIONAL RESPONSE SURFACES FROM PROCESS DATA - Finding Optimal Set Points for Machine Control.
DOI: 10.5220/0003408703970404
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 397-404
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

random vector with
nxn
ICovE == ][ ,0][
ε
ε
(3)
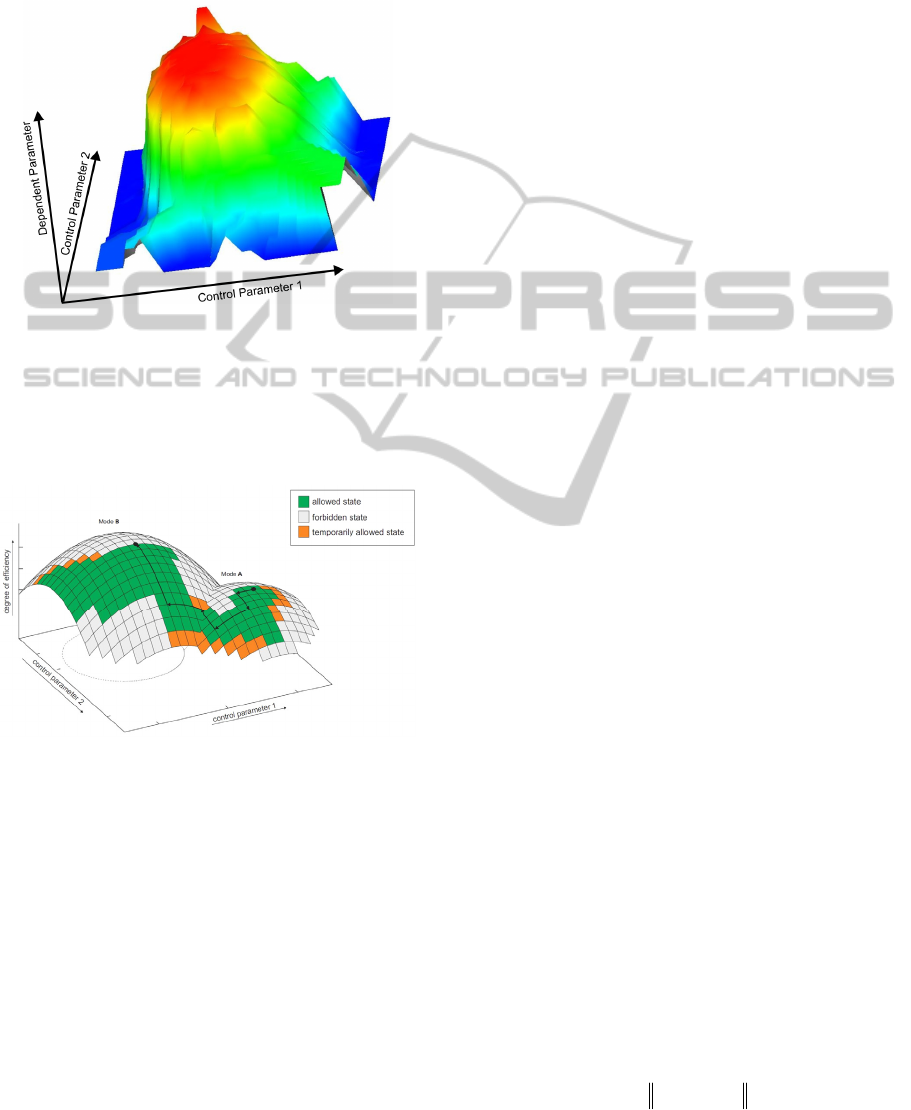
Figure 1 shows, in the special case of n=2 and m=1,
a practical example of a response surface:
Figure 1: Empirical Response Surface.
Please note that the data underlying this figure as
well as the following figure are arbitrarily selected
from among the authors' pool of data and only serve
the purpose to explain principles.
Figure 2 shows a schematic idealization:
Figure 2: Schematic Idealization.
There is one – particularly important – example for
the use of response surfaces in controlling industrial
processes. Assume that in a fossil power plant such
as a gas turbine, two of the response variables are
given by the power output and the NO
x
emissions,
while one particularly important independent
variable is the gas inflow. It may then be of interest
to find that particular input variable
n
Rx ∈*
which
maximizes power output given gas inflow and an
upper limit on the NO
x
emissions or minimizes gas
inflow for given power output and - again - an upper
limit on the NO
x
emissions etc. In other words, one
is interested in maximizing efficiency for given
power output under additional conditions.
This optimal value can be found in a twofold
procedure, whereby the first step consists in finding
the m response surfaces corresponding to the m
response variables given by formula (1) and the
second step is expressed as
)(
1
xfMax
n
Rx∈
(4)
such that
g(x)f
<
=
2
(5)
and
03
f(x)f
≤
(6)
where f
1
(x), f
2
(x), f
3
(x), p and f
0
are power output,
gas inflow, emissions, gas available and emission
limit, respectively.
In a third step, whenever a process is in a state
n
Rx ∈ a sequence of “control variables” must be
found, which drives the process towards the optimal
state
n
Rx ∈* .
In this paper it is shown how to find the
functional relationship f, how to use this in order to
find an optimal operating point under given
constraints and how to use the optimal operating
point in an adaptive control policy. An example
concludes this research.
It is to be noted that the time dependency
between signal records plays no role in this paper,
because, in finding optimal operating points, as well
as regression with given input variables as
arguments, time is not used as a regressor. Therefore
time series analysis as expressed in ARMA or
ARMAX techniques (Bhattacharya, 2009) remains
in the background.
3 FINDING THE RESPONSE
SURFACE
This step asks for the solution of a certain type of
multidimensional approximation problem, wherein -
simultaneously - m real functions of n real variables
are to be approximated.
3.1 The Least Squares Principle
The method suggested in this paper uses the least
squares principle where the objective function is to
be minimized by an appropriate selection of the
function f. While classical response surface
∑
=
−=
M
i
ii
xfyfZ
1
2
)(:)(
(7)
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
398

methodology mostly works with quadratic forms of
the response variable with respect to the input
variables, see for instance (Myers, 2009) and
(Oezer, 2004), in this paper f is to be selected from
among the more general set of twice continuously
differentiable functions mapping
n
R
onto
m
R
.
From the practical point of view this requires an
idea about the functional dependence of f(x) on
n
Rx ∈ . Once this functional relationship is
established and expressed in a formula with
appropriate parameters, minimization over the
function space is reduced to minimization over the
appropriate parameter space.
3.2 Linear Combinations of Gaussian
Shapes
A possible choice for the functional relationship is
an element-wise linear combination of Gaussian
shapes such that
)()(
1
)(
1
1
)()()(
)(
:
:)(:),,;(:)(
j
k
j
k
T
j
k
j
xAx
N
k
j
k
m
j
j
j
m
j
j
ece
xfeAcxfxf
μμ
μ
−−−
==
=
∑∑
∑
=
===
(8)
In (8) e
j
is the unit vector in j-direction, N
(j)
is the
number of Gaussian shapes used in approximating
f
j
(x), c
k
(j)
,
},...,1{
)( j
Nk ∈
is the height of the k-th
shape for the corresponding element,
μ
k
(j)
is the
corresponding location vector and A
k
(j)
the
corresponding shape matrix. The symbols c,
μ and A
are abbreviations as explained in the appendix. An
additional stipulation is that the matrices A
k
(j)
are
required to be positively definite. Moreover, with
this choice of functional representation, one works
with functions that are infinitely often - not just
twice - continuously differentiable. Also these
functions tend towards zero with either of its
arguments going to infinity, having no poles or wild
erratic oscillations and therefore, being less prone to
overfitting the data.
Expanding the Euclidean norm in (7) it can be
seen that
},...,1{
)²,(
))²((:)(
with)()(
)()(
1
)(
1
)(
1
)(
1
)()()(
)(
mj
ecy
xfyfZ
fZfZ
j
k
i
j
k
Tj
k
i
j
xAx
N
k
j
k
M
i
j
i
ij
M
i
j
ijj
j
m
j
j
∈
−
=−=
=
−−−
==
=
=
∑∑
∑
∑
μμ
(9)
The minimization method for the objective function
amounts to solving separately m individual
minimization problems with the objective functions
Z
j
(f
j
). Each of these minimization problems requires
finding values for the decision variables
()
()
() ()
() ²
{1,..., }
{1,..., }
{1, . . . , }
j
j
k
jn j
k
jn
k
NM
cR
jm
Rk N
AR
μ
⎫
∈
⎪
⎫
∈
⎪
∈
⎪
⎬
∈∈
⎬
⎪
⎪
⎪
∈
⎭
⎭
(10)
Since N
(j)
is a discrete parameter and all other
parameters are real, the minimization problems are
mixed integer real. Therefore, if derivative based,
non-linear minimization techniques are to be used
such as Fletcher-Reeves etc., see (Press, 2007), one
must resort to a trick, whereby N
(j)
is deliberately
given a sufficiently high value and it is left to the
height variables c
k
(j)
to emphasize and eventually
eliminate one or the other of the Gaussian shapes.
Even if this trick works, there is always the risk of
being trapped in a local minimum.
Both problems can be overcome simultaneously
by using a local search technique such as Simulated
Annealing, for instance, see (Press, 2007) and
(Rayward-Smith, 1996).
It is important to note that for each input dataset
MiRRyx
mn
ii
,...,,),( ∈×∈
(11)
there is a representation (8) which approximates the
response variables to any desired degree of
precision, the exact proof of which is very technical
and will be omitted here. The proof follows along
the following lines, however: For each response
variable one begins with M shapes, each as high as
the corresponding response variable and located
right at the corresponding input point, with an
arbitrary shape matrix. The shape matrices are then
narrowed down consecutively until for each shape,
the impact of remote shapes is small enough to
satisfy the precision requirement.
3.3 A Note on Overfitting
Like any approximation problem on the real line, it
is necessary to limit the risk of overfitting by
checking the goodness of fit of the minimization
routine on a validation set of points, which are not
used in tuning the model parameters. This task is
currently in progress between the authors.
GENERATING MULTIDIMENSIONAL RESPONSE SURFACES FROM PROCESS DATA - Finding Optimal Set
Points for Machine Control
399

4 FINDING THE OPTIMAL
POINT ON THE RESPONSE
SURFACE
In contrast to (Ribeiro, 2010) the analysis described
in the present paper considers only one response
variable, which determines the optimal operating
point, while more than one response variable may
appear in the constraints.
This step will be analyzed under the two
different scenarios of unconstrained and constrained
optimization.
4.1 Unconstrained Optimization
Assume that one arbitrary response variable
},...,1{* mj ∈
(12)
is to be maximized, i.e.
)(*)(
**
xfMaxxf
j
Rx
j
n
∈
=
(13)
Two special cases must be considered. In case 1
one assumes that N
(j)
=1. Then, due to the positive
definiteness of the shape matrices as required above
and the monotonicity of the natural logarithm,
maximizing f
j*
(x) with respect to x is equivalent to
minimizing
(*) (*) (*)
11 1
(): ( ) ( )
jT j j
xx Ax αμ μ =− −
(14)
which yields the simple result
*)(
1
*
j
x μ =
(15)
In case 2, i.e. whenever N
(j)
>1, one must either
use a non-linear search technique with several
randomized starting points or a local search
technique. In view of (15), a plausible choice for the
starting point may be
∑
∑
=
=
=
*)(
*)(
1
*)(
*)(
1
*)(
0
j
j
N
k
j
k
j
k
N
k
j
k
c
c
x
μ
(16)
There is a variety of such search techniques, as
can be seen in (Press, 2007) and (Speyer, 2010), for
example. However, simple application of the first
order necessary conditions of any optimal point to
f
j*
(x), i.e.
0)(
*
=
∇ xf
j
(17)
yields, along with (8), the following equation:
)(*)(
1
xbxHx
jj
−
=
(18)
with
)()(
1
)()(
)(
1
)(
)()(
)(
)(
)()()(
)(
)()()(
:)(
:)(
j
k
j
k
N
k
xAx
j
kj
N
k
j
k
xAx
j
kj
Aecxb
AecxH
j
j
k
j
k
T
j
k
j
j
k
j
k
T
j
k
μ
μμ
μμ
∑
∑
=
−−−
=
−−−
=
=
(19)
Observing that in (18) the right hand side
depends on x as well, one may try to find an iterative
expression with
...3,2,1
)(*)(
)1(1)1()(
=
=
−−−
k
xbxHx
k
j
k
j
k
(20)
hoping, for the time being, that H
j
(x) is invertible
and (20) represents a contracting map. (20) may be
generalized to the case of constrained optimization
using the Lagrange function or a penalty term. In
any case observe, that it bears a certain resemblance
to the quadratic programming problem.
4.2 Constrained Optimization
As a representative of the multitude of potential
constrained optimization problems assume that one
must maximize a particular response variable j*
while all the other ones are to stay within a certain
upper limit, which amounts to solving the following
minimization problem:
*}{},...,1{,)(
))((
,0
*
jmjfxf
xfMin
jj
j
Rx
n
−∈≤
−
∈
(21)
Introducing a slack variable
1m
j
R
ξ
−
∈
(22)
one easily sees that solving (21) is equivalent to
solving a non-linear minimization problem with the
following Lagrangian:
∑
−∈
−−
+
−
=
*}{},...,1{
,0
*
²))((
))(();(
jmj
jjjj
j
xff
xfxL
ξλ
λ
(23)
see (Speyer, 2010). Finding a solution to (23) with a
derivative based non-linear minimization technique
may be attempted by a large scale Sequential
Quadratic Programming Problem such as described
in (Gill, 2005), for instance.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
400

However, in this situation local search heuristics
can be used again by noting that the objective
function -f
j*
(x) can be augmented by a penalty
function which assumes increasingly high values, if
the constraints
*}{},...,1{,)(
,0
jmjfxf
jj
−∈≤
(24)
are violated. The smallest such penalty function can
then be used in the solution.
5 APPROACHING THE
OPTIMAL POINT ON THE
RESPONSE SURFACE
Assume that, at a certain time
,...}3,2,1{,* ∈Δ= ltlt
(25)
throughout operation of the process under
consideration, the process state is equal to
n
Rx ∈
~
(26)
with
*
~
xx ≠
(27)
indicating operation under sub-optimal conditions. It
is then important to find a sequence of control
variables
ww
RuRu ∈∈
τ
,...,
1
(28)
for some
,...}3,2,1{∈w
(29)
and some
,...}3,2,1{∈
τ
(30)
5.1 Deterministic Case
Here one assumes that
*),(
...
),(
~
1
111
xuxxx
uxxx
xx
ttt
ttt
t
==
=
=
−+++
++
ττττ
(31)
Assume there is a cost
γ (x
t+k-1
,u
k
) attached to the
transition
1
,,{1,...,}
tk k tk
xuxk
τ
+− +
→∈
(32)
The total transition cost is then given by
∑
=
−+
=
τ
τ
γ
1
11
),(:),...,,(
k
kktt
uxuuxC
(33)
As long as a transition law as given in (31) can be
found, (33) can be - again - minimized using either
non-linear minimization or local search.
5.2 Stochastic Case
Assume that the transition from x
t+k-1
to x
t+k
under
the control u
k
, k=1,2,..., τ takes place in a stochastic
manner such that the distribution density of x
t+k
is
given by a density
1
(; , ):
nw n
tk k
gzx u R R
+
+−
→
(34)
The expected cost under the control policy u
1
,...,u
τ
is
given by
dzuxzguuzC
uxuuxC
t
R
tt
n
),;(),...,,(
),(),...,,(
12
11
∫
+
+=
τ
τ
γ
(35)
The optimal policy u
1
*,...,u
τ
∗ leading to the minimal
expected cost C*(x
t
,u
1
*,...,u
τ
*) satisfies the
Bellman equation
}*),;()**,...,,(*
*),({
*)*,...,,(*
12
1
*
1
1
dzuxzguuzC
uxMin
uuxC
t
R
t
Ru
t
n
w
∫
+
=
∈
τ
τ
γ
(36)
see (Bhattacharya, 2009). The Bellman-equation can
be solved by means of the classical dynamic
programming approach and - again - by local search
techniques such as Simulated Annealing.
6 EXAMPLE
The problem considered in this example consists in
solving efficiency related optimization problems for
an input file with n = 8 independent variables and m
= 2 response variables. The two response variables
considered are power output and NO
x
emissions. M
= 4560 records were available. The data correspond
to a gas turbine in a French power plant. All of the
signals have been normalized to values between 0.0
and 1.0 each.
As a constrained optimization problem Power
output (response variable 1) will be maximized
while a series of constraints, partly referring to gas
inflow - one of the control variables - and partly
referring to NO
x
emissions (response variable 0) will
GENERATING MULTIDIMENSIONAL RESPONSE SURFACES FROM PROCESS DATA - Finding Optimal Set
Points for Machine Control
401

be imposed. It will be shown that the data contained
in the input file, when filtered with respect to those
constraints, already exhibit some variance in
response variable 1, without the smoothing effect
brought about by response surface modelling.
6.1 Input Data
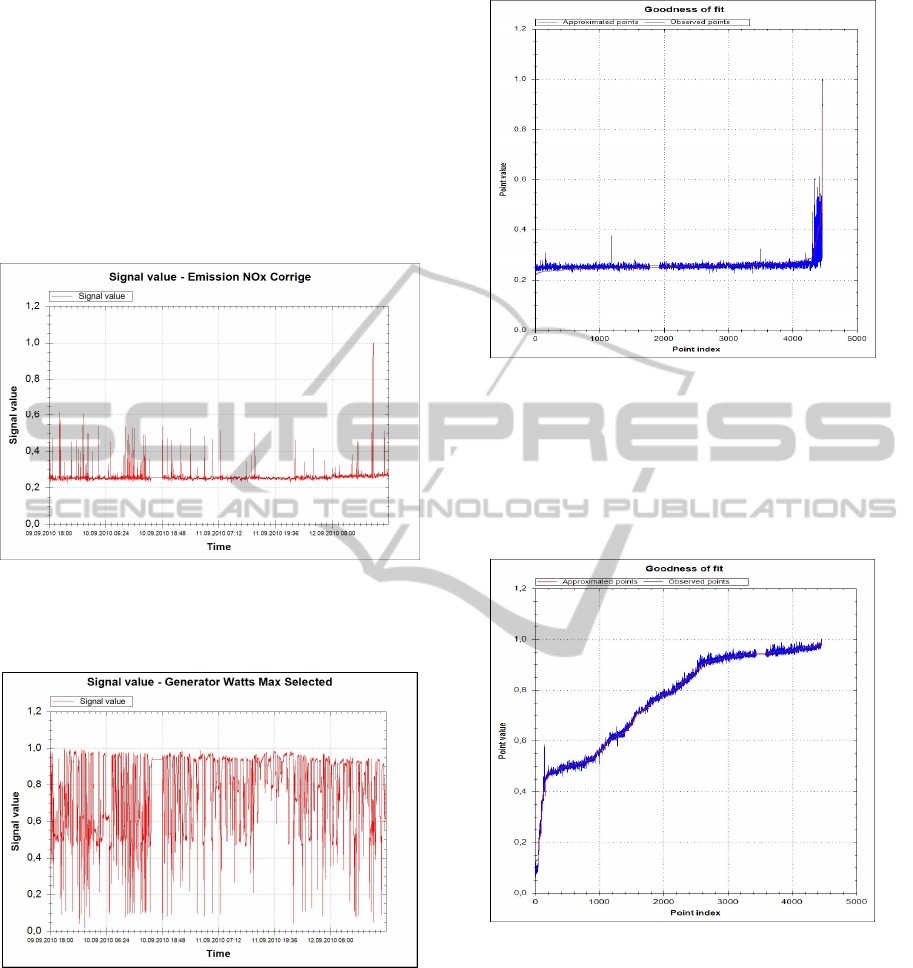
Figure 3 shows the time trajectory of the NO
x
emissions throughout the time period under
consideration:
Figure 3: NO
x
emissions - Time Trajectory.
Figure 4 shows the time trajectory of the power
output:
Figure 4: Power output - Time Trajectory.
6.2 Results
Results for this example are given for steps 1 and 2
only. Developing optimum control policies is
ongoing research at this time.
6.2.1 Approximation
Figure 5 shows the goodness of fit for NO
x
emissions as a result of the approximation:
Figure 5: NO
x
emissions - Goodness of Fit.
Please note that - for ease of comparison - the
approximated points have been ordered increasingly
with respect to size and that the corresponding input
values, i.e. those with equal input variables have
been juxtaposed accordingly. Figure 6 shows the
goodness of fit for the power output:
Figure 6: Power output - Goodness of Fit.
Figure 7 shows a three-dimensional representation
of the empirical power output as contained in the
input data as a function of the input variables 0 and
1 (Barometric pressure and Compressor inlet
pressure, see below), whereby all the remaining
input variables have been set equal to their
respective midpoint between minimum and
maximum:
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
402

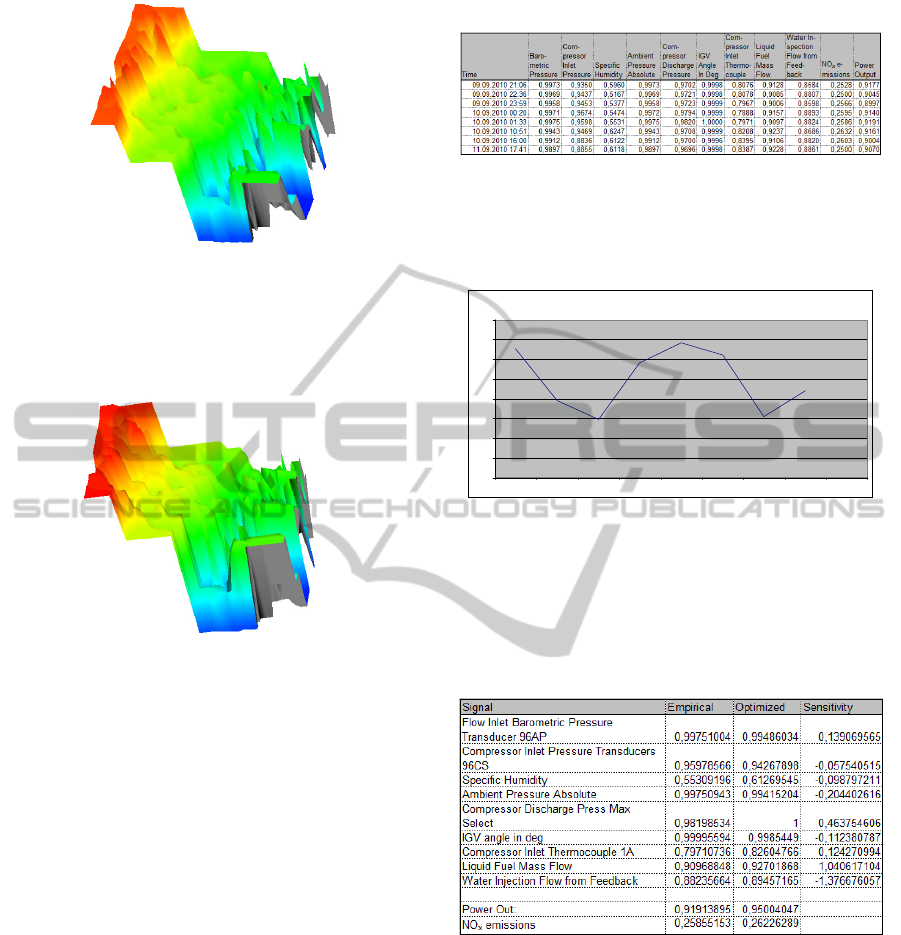
Figure 7: Three-dimensional representation of empirical
power output with respect to control variables 0 and 1.
Figure 8 is the analogous representation with the
empirical power output replaced by its theoretical
counterpart obtained from approximation:
Figure 8: Three-dimensional representation of theoretical
power output with respect to control variables 0 and 1.
The good visual agreement between figures 7 and 8
is another view on the goodness of fit as shown in
figure 6.
6.2.2 Efficiency Maximization
Optimization Problem
The problem considered was to maximize Power
output under the following constraints:
 Compressor Discharge Pressure >= 97% of
Maximum
 NO
x
emissions <= 40% of Maximum
 IGV guide angle >= 99,90% of Maximum
 Liquid Fuel Mass Flow <= 93% of
Maximum
 Water Injection flow <= 89,4% of
Maximum
Input Data Filtered with Respect to Constraints
Table 1 shows the subset of input data resulting
from filtering the records with the constraints as
shown above:
Table 1: Input data filtered with respect to constraints.
Table 1 reveals that already within the filtered
dataset power output shows a variance of roughly
2% with respect to the maximum value of 1.0,
keeping the normalized range of values in mind, as
illustrated in figure 9:
Power Output
0,885
0,89
0,895
0,9
0,905
0,91
0,915
0,92
0,925
123456789
Figure 9: Variance in power output in the filtered dataset.
Optimization Results
Table 2 shows the mathematical solution to the
optimization problem stated above with respect to
both input variables and response variables:
Table 2: Optimization Results.
The following comments must be made in order to
properly interpret these results:
 The column titled Empirical lists the values of
all the input variables corresponding to that
particular record in the filtered input file - see
table 1 - with maximum overall power output.
 This goes along with an NO
x
emission value of
25.85 % of the maximum as shown in the
corresponding line and 91.91% of maximum
power.
 The column titled Optimized lists the values of
the input variables corresponding to the solution
of the constrained optimization problem. It can
GENERATING MULTIDIMENSIONAL RESPONSE SURFACES FROM PROCESS DATA - Finding Optimal Set
Points for Machine Control
403

be noted that all of the constraints are satisfied
to a good degree of precision:
o Compressor Discharge Pressure = 100% >=
97% of maximum
o NO
x
emissions = 26,23% <= 40% of
maximum
o IGV angle = 99.85% <= 99.9% required
o Liquid Fuel Mass Flow = 92.70% of
maximum versus <= 93% required
o Water Injection flow = 89,45% of
maximum versus 89,4% required
 Yet there is a theoretical increase in the Power
output of approximately 3.09%=95.00%-
91.91%. Comparison of the ratio of Power
output divided by Liquid Fuel Mass Flow
reveals an efficiency increase from the optimal
element in the filtered dataset to the
mathematical solution of the constrained
optimization problem of 1.43%.
 The column titled Sensitivity is the partial
derivative of the Power Output with respect to
the input variable in question, averaged over the
input space using the sample of input data.
 It must be noted that the solution to the
optimization problem must be verified against
the criteria of technological feasibility. For
instance, turbine inlet temperature must not
exceed a fixed value and no optimal operating
point must violate this additional constraint.
7 SUMMARY
The present paper presents a technique to generate
Gaussian response surfaces from high dimensional
data and shows how to use them to find optimal
operating points with respect to process
characteristics such as Power output, NO
x
-
emissions, gas inflow etc.
There are two sources of optimization to be
expected through an industrial application of such
surfaces:
• Finding true optima by removing noise in the
data and appropriate smoothing
• Consistently using those optima as set points
in the context of adaptive control.
From the authors' point of view, many of the topics
considered in this paper will be central to future
research in the power industry around the world,
such as
• Fast optimization techniques in finding the
response surfaces, using a combination of non-
linear and local search techniques
• Fast optimization techniques to find the optimal
points on the response surfaces
• Embedding the algorithms inside machine
control hardware and software to name just a
few.
ACKNOWLEDGEMENTS
Our thanks go to our co-workers Sebastian Feller,
Yavor Todorov and Dirk Pauli for valuable hints in
numerical optimization techniques and to Tina
Condon for careful proof reading.
REFERENCES
Bhattacharya, R. N., Waymire, E. C. 2009. Stochastic
Processes with Applications. Society for Industrial
and Applied Mathematics (SIAM), Philadelphia
Gill, P. E., Murray, W., Saunders, M. A. 2005. SNOPT: A
large Scale SQP Algorithm. SIAM Review 47 (2005),
99-131
Myers, R. H., Montgomery, D. C., Anderson-Cook, C. M.
2009. Response Surface Methodology, Process and
Product Optimization Using Designed Experiments.
Wiley, Hoboken (2009)
Oezer, E. A., Ibanoglu, S., Ainsworth, P. 2004. Expansion
characteristics of a nutritious extruded snack food
using response surface methodology. Eur. Food Res.
Technol. 218 (2004), 474-479
Press, H. W. et al. 2007. Numerical Recipes, The Art of
Scientific Computing. Cambridge University Press;
Cambridge, MA, USA
Rayward-Smith, V. J. et al. (Eds.) 1996. Modern Heuristic
Search Methods. Wiley, Chichester
Ribeiro, J. S., Teófilo, R. F., Augusto, F., Ferreira, M. M.
C. (2010). Simultaneous optimization of the
microextraction of coffee volatiles using response
surface methodology and principal component
analysis. Chemometrics and Intelligent Laboratory
Systems 102 (2010), 45-52
Speyer, J. L., Jacobson, D. H. 2010. Primer on Optimal
Control Theory. Society for Industrial and Applied
Mathematics (SIAM), Philadelphia
APPENDIX
Definition of c, μ and A:
}},...,1{},,...,1{,{:
)()(
mjNkcc
jj
k
∈∈=
}},...,1{},,...,1{,{:
)()(
mjNk
jj
k
∈∈= μμ
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
404