
POSSIBILISTIC METHODOLOGY FOR THE EVALUATION
OF CLASSIFICATION ALGORITHMS
Olgierd Hryniewicz
Systems Research Institute, Polish Academy of Sciences, Newelska 6, Warsaw, Poland
Keywords: Classification, Accuracy, Statistical tests, Multinomial distribution, Comparison of algorithms, Possibility
and necessity indices.
Abstract: In the paper we consider the problem of the evaluation and comparison of different classification
algorithms. For this purpose we apply the methodology of statistical tests for the multinomial distribution.
We propose to use two-sample tests for the comparison of different classification algorithms, and one-
sample goodness-of-fit tests for the evaluation of the quality of classification. We restrict our attention to the
case of the supervised classification when an external ‘expert’ evaluates the correctness of classification.
The results of the proposed statistical tests are interpreted using possibilistic indices of dominance
introduced by Dubois and Prade.
1 INTRODUCTION
Algorithms used for the purpose of classification of
observations (data points, data records) constitute an
important part of machine learning. They are divided
in two general groups: classification algorithms used
in processes of supervised learning, and data
clustering algorithms used in processes of
unsupervised learning. In this paper we will discuss
the problem of the evaluation of the quality of the
algorithms used for classification, usually
understood as the accuracy of classification. A
natural measure of such quality is the percentage of
correctly classified objects, usually called
classification accuracy. This measure is used by all
authors of papers devoted to classification problems,
both developers of new algorithms, and users of
existing algorithms who apply them for solving
practical problems.
The evaluation of the quality of classification
using the accuracy index may not be sufficient. In a
rather simple case of only two possible classes the
observations have to be classified to, statisticians
advise to use two additional indices whose
background can be found in medical sciences,
namely the indices of sensitivity and specificity. Let
us assume that considered objects can be assigned to
two disjoint classes called ‘positive’, and ‘negative’.
By sensitivity (also known in machine learning as
recall) we understand the conditional probability
that the object which should be classified to the
‘positive’ class has been correctly assigned to this
class. By specificity (also known in machine
learning as recall of negatives) we understand the
conditional probability that the object which should
be classified to the ‘negative’ class has been
correctly assigned to this class. For good
classification rules the values of these indices should
be both close to one. In machine learning some
functions of these indices (e.g. F-measures or ROC
diagrams) are used. For more information see e.g.
Chapter 7 in (Berthold and Hand, 2007).
The problem of the evaluation of the quality of
classification becomes more difficult when the
number of possible classes is larger than two. In
such cases many different criteria have been
proposed. Some of them, like the error correlation
EC, have probabilistic interpretation, but the
majority of them are based on some heuristics. For
more information on this subject see e.g Chapter 11
in (Nisbet et al., 2009). The major disadvantage of
all these measures stems from the fact that they
usually do not have any statistical interpretation.
Without such interpretation we are not able to
present statistically sound comparison of different
algorithms.
In this paper we propose to use the methodology
of statistical tests to evaluate and compare the
quality of classification algorithms. The
mathematical background for these evaluations and
313
Hryniewicz O..
POSSIBILISTIC METHODOLOGY FOR THE EVALUATION OF CLASSIFICATION ALGORITHMS.
DOI: 10.5220/0003436803130322
In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 313-322
ISBN: 978-989-8425-77-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

comparisons is presented in second and third
sections of the paper. In these sections we consider
two cases. In the first one, considered in the second
section, we compare the performance of different
classification algorithms using two-sample tests for
the multinomial distribution. In the second case,
considered in the third section, we use the
multinomial goodness-of-fit tests for the evaluation
of the accuracy of classification algorithms. In the
fourth section of the paper we propose new
possibilistic measures for the comparison of
classification algorithms. This measures are based
on the possibilistic interpretation of statistical tests
proposed in (Hryniewicz, 2006). The paper is
concluded in the fifth section where problems for
future considerations are also formulated.
2 STATISTICAL COMPARISON
OF THE PERFORMANCE
OF CLASSIFICATION
ALGORITHMS
Let us assume that we have to classify n objects into
K disjoint classes. In this paper we restrict ourselves
to the case when the classification algorithm
classifies each object to only one of possible classes.
We do not impose any restriction on the type of the
algorithm used for this purpose. This can be artificial
neural network classifier, set of classification rules,
vector supporting machine classifier, Bayes naïve
classifier or any other algorithm that can be
proposed for this purpose. Moreover, we assume that
there exists a method for the evaluation of the
correctness of the classification of each considered
object. This can be an expert, as in the case of
classical supervised learning, or the algorithm that
assigns the object to a class formed by a certain
clustering algorithm, as in the case of unsupervised
learning.
Let
()
121 +KK
n,n,,n,n …
be the vector
describing the evaluation of the accuracy of the
considered classification algorithm. First K
components of this vector represent the numbers of
cases of the correct classification to K considered
classes. The last component gives the total number
of incorrectly classified objects. Thus, in this model
we do not distinguish possibly different types of
misclassification. If we do need to distinguish them
we could expand this vector by adding additional
components.
Let us assume now that observed values of
()
121 +KK
n,n,,n,n …
represent a sample from an
unknown multinomial distribution, defined by the
probability mass function
()
∏
+
=
+
+
=
1
1
11
11
K
i
n
i
K
KK
i
p
nn
n
p,p,,pMB
!!
!
…
,
(1)
where
∑
+
=
=
1
1
K
i
i
nn , and
∑
+
=
=
1
1
1
K
i
i
p , that describes
a hypothetical population of objects classified in a
similar way to that used for the classification of the
considered sample.
Now, let us suppose that we have to compare
two classification algorithms, whose results of
application are given in the form of two vectors
()
121 +KK
n,n,,n,n …
, and
()
121 +KK
m,m,,m,m …
,
respectively. First, let us consider the case that both
algorithms are compared using the same set of
observations. Thus, n=m, and both observed vectors
are statistically dependent. In such case in order to
compare the considered algorithms we have to know
the results of the classification of each object, and
then to use statistical methods devised for the
analysis of pair-wise matched data. Unfortunately,
this can be easily done only in the case when we
have data that can be summarized in the following
table
Table 1: Dependent test data.
Alg.1 -correct Alg.1 - incorrect
Alg. 2-correct k
11
k
12
Alg. 2 - incorrect k
21
k
22
In this table k
11
is the number of objects classified
correctly by both algorithms, k
12
is the number of
objects classified correctly by Algorithm 1 but
incorrectly by Algorithm 2, k
21
is the number of
objects classified correctly by Algorithm 2 but
incorrectly by Algorithm 1, and k
22
is the number of
objects classified incorrectly by both algorithms.
Using statistical terminology we can verify two
hypotheses. First hypothesis is that the probabilities
of incorrect classification for both compared
algorithms are the same, and is tested against the
alternative that they are simply different. In this case
we have to apply the so called two-sided statistical
test. We may consider the statistical hypothesis that
one algorithm is not worse (i.e. better or the same)
than the other one, and test it against the hypothesis
that it is worse. In this case we have to apply the so-
called one-sided statistical test.
When both compared probabilities are equal it is
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
314

known, see e.g. (Agresti, 2006) for more
information, that the number of incorrect
classifications k
21
is described by the Binomial
probability distribution with the parameters
k=k
12
+k
21
and p=0,5. Let us assume now that we
observe
∗
and
∗
incorrectly classified (only by
one algorithm!) objects. The probability of
observing these data can be calculated from the
following formula
∗
|
∗
=
∗
+
∗
=
∗
∗
∗
∗
∗
.
(2)
In order to verify the hypothesis of equal
probabilities of misclassification we have to
calculate, according to (1), probabilities of all
possible pairs
,
∗
. In case of the two-sided test
the sum of those probabilities that do not exceed the
probability of the observed pair
∗
,
∗
give the
value of the significance (known also as the p-value)
of the tested hypothesis. When this value is greater
than 0,05 it is usually assumed that the hypothesis of
the equal probabilities should not be rejected. In case
of the one-sided test we consider only these pairs
,
∗
who support the one-sided alternative.
Thus, the p-value in case of the one-sided alternative
is smaller than in the case of the two-sided
alternative. Hence, it is easier to reject the
hypothesis that one algorithm is not worse than the
other one than to reject the hypothesis that they are
statistically equivalent.
When the number of incorrectly classified
objects k
*
is sufficiently large (in practice it is
required that the inequality k
*
>10 must be fulfilled)
the following statistic
=
−
+
(3)
is approximately distributed according to the chi-
square distribution with 1 degree of freedom. This
statistic is used in the well known McNemar test of
the homogeneity of proportions for pair-wise
matched data.
Let us consider the example of Fisher’s famous
Iris data (available at the web-site of the University
of California, Irvine). We use this benchmark set for
the comparison of two algorithms: LDA (Linear
Discrimination Analysis) and CRT (Classification
Regression Tree) – both implemented in a popular
statistical software such as e.g. STATISTICA. For
more information about these algorithms see e.g.
(Krzanowski, 1988). The results of the comparison
are given in Table 2
Table 2: Comparison – IRIS dataset.
LDA -correct LDA - incorrect
CRT-correct 147
1
CRT - incorrect 0 2
The p-value in this case is easily computed, and
is equal to 1. Therefore, the obtained statistical data
do not let us to reject the hypothesis that the
probabilities of incorrect classification are in case of
these two algorithms the same.
Iris data are well separable, so from a statistical
point of view all classification algorithms tested on
this benchmark set are indistinguishable. The
situation is different in the case of data considered in
(Charytanowicz et al., 2010). We will use these test
data for the comparison of two algorithms: Bayesian
algorithm proposed in (Kulczycki and Kowalski,
2011) and classical QDA algorithm described in
(Krzanowski, 1988). The results of the comparison
are presented in Table 3.
Table 3: Comparison – Wheat kernels.
Bayes -corr. Bayes - incorrect
QDA-correct
85
9
QDA -
incorrect
5 6
The p-value in this case is equal to 0,42.
Therefore, the obtained statistical data do not let us
to reject the hypothesis that the probabilities of
incorrect classification are in the case of these two
algorithms the same despite the fact that one of the
compared algorithms (QDA) seems to be
significantly better (nearly 30% lower probability of
incorrect classification).
When we do not have an access to individual
results of classification we can compare algorithms
using independent samples described by the
multinomial distributions. Let the data be described
by (1), and
∑
+
=
=
1
1
K
i
i
nn and
∑
+
=
=
1
1
K
i
i
mm be the
sample sizes which in general do not have to be
equal. Moreover, note that in case when one of these
algorithms is a perfect classifier (e.g. a domain
expert) we have
0
1
=
+K
n
(or
0
1
=
+K
m
). If the
results of the application of the first algorithm are
described by the multinomial distribution
()
11 +KK
p,p,,pMB …
, and the results of the
application of the second algorithm are described by
POSSIBILISTIC METHODOLOGY FOR THE EVALUATION OF CLASSIFICATION ALGORITHMS
315

the multinomial distribution
()
11 +KK
q,q,,qMB …
their performance can be compared by testing the
statistical hypothesis
11110 ++
===
KKKK
qp,qp,,qp:H …
.
(4)
To test this hypothesis we may apply
methodology of two-way contingency tables. Test
data are now presented as the following table
Table 4: Independent test data.
Alg./Class 1 … j … K K+1 Total
Alg. 1 n
11
… n
1j
… n
1K
n
1K+1
N
Alg. 2 n
21
… n
2j
… n
2K
n
2K+1
M
Total c
1
… c
j
… c
K
c
K+1
N+M
When the hypothesis H
0
given by (4) is true, the
conditional distribution of observed random vectors
()
121 +KK
n,n,,n,n …
, and
()
121 +KK
m,m,,m,m …
,
given the vector of their sum
()
121 +KK
c,c,,c,c …
, is
given by the multivariate hypergeometric
distribution (Desu and Raghavarao, 2004)
()
∏
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
1
1
0
K
i
i
i
n
c
N
nm
H,|;P
!
!!
cmn
.
(5)
This probability function is used for the construction
of the multivariate generalization of Fisher’s exact
test that is used for the verification of (4). Let
n
*
, m
*
,
and c
*
be the observed data vectors. The p-value
(significance) of the test is computed from the
formula (Desu and Raghavarao, 2004)
()
(
)
∑
∗
=−
Γ
0
H,|,Pvaluep cmn
,
(6)
where
()
(
)
(
)
{
}
00
H,|,PH,|,P,
∗∗∗∗
≤= cmncmnmn :
Γ
(7)
The p-values of this test can be computed by the
tools of statistical packages such as SPSS or SAS.
It can be shown that the test of the equality of
two sets of multinomial probabilities is formally
equivalent to the test of independence of categorical
data. Hence, for testing (4) it is also possible to use a
popular test of independence – Pearson’s chi-square
test of independence. This test can be use only in
case when the total number of observations is large
(greater than 100), and in each cell of the
contingency table it is more than 5 observations.
These assumptions are usually fulfilled in testing
classification algorithms, except for situations were
tested data allows building perfect or nearly perfect
classifiers. However, in such cases the problem of
choice of the best classifiers does not exist.
The
2
χ
statistic in the considered case can be
written as
() ()
∑∑
+
=
+
=
−
+
−
=
1
1
2
1
1
2
2
K
i
i
ii
K
i
i
ii
m
ˆ
m
ˆ
m
n
ˆ
n
ˆ
n
χ
,
(8)
where
N
nc
n
ˆ
i
i
=
,
(9)
and
N
mc
m
i
i
=
ˆ
.
(10)
The p-value for this test is obtained by solving, with
respect to p, the equation
2
1
2
p,K −
=
χχ
,
(11)
where
2
1 p,K −
χ
is the quantile of order 1-p in the chi-
square distribution with K degrees of freedom. Also
in this case the p-values of Pearson’s chi-square test
of independence can be computed using the tools
available in statistical packages such as SPSS or
SAS.
In order to illustrate the application of the
proposed tests in the evaluation of classification
algorithms let us first consider a hypothetical
example of the classification of N=100 objects into
K=3 classes. Suppose that we want to compare three
algorithms A, B, and C, together with a “perfect”
algorithm represented by an expert E. All compared
“imperfect” algorithms have their ‘normal’ and
‘improved’ versions indexed by subscripts 1 and 2,
respectively. All incorrect (false) classifications are
assigned to the additional fourth class. Suppose that
the results of this hypothetical experiment are
presented in Table 5.
Algorithms A, B and C in their both versions are
characterised by the same total percentages of
incorrect classification equal to 10% and 5%,
respectively. However, the distribution of incorrectly
classified objects depends upon the used algorithm.
In case of algorithm A incorrectly classified
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
316
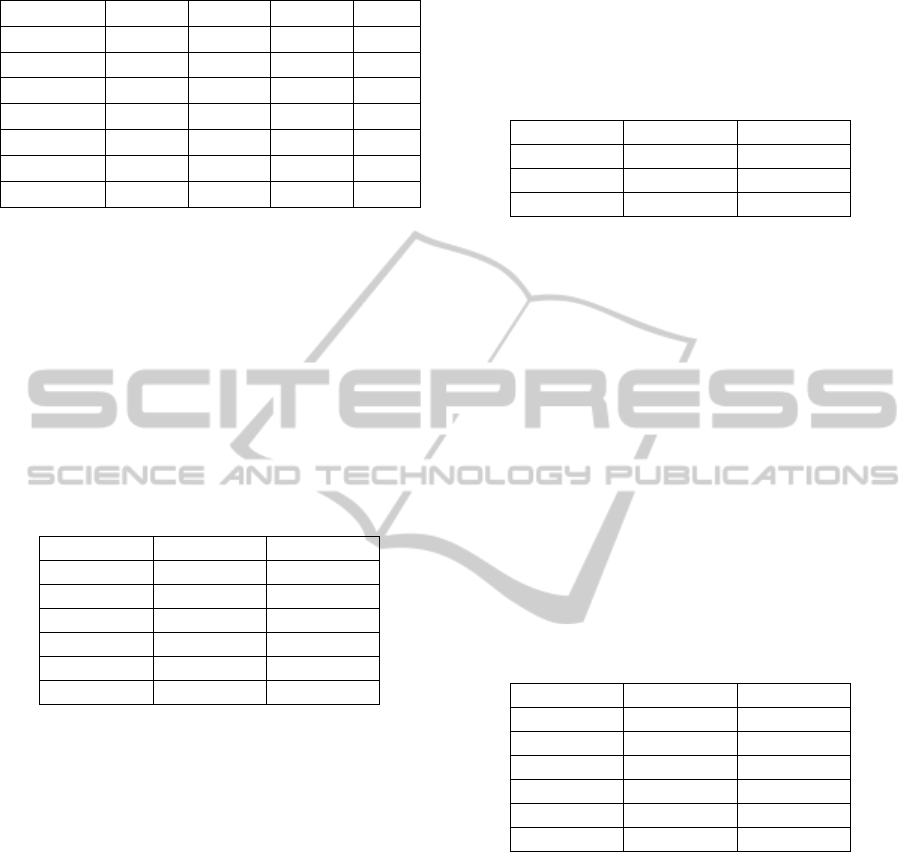
Table 5: Results of a hypothetical experiment.
Alg.\Class 1 2 3 4
Expert 20 30 50 0
A
1
18 27 45 10
A
2
19 29 47 5
B
1
10 30 50 10
B
2
15 30 50 5
C
1
20 30 40 10
C2 20 30 45 5
objects are distributed proportionally to the actual
sizes of classes. For algorithm B all incorrectly
classified objects are assigned to the class with the
lowest number of actual observations. Finally, in
case of algorithm C all incorrectly classified objects
are assigned to the class with the highest number of
actual observations.
In Table 6 we present the p-values of both
considered tests when the performance of each
classification algorithm is compared to the
classification given by the expert.
Table 6: Comparison with the expert.
Fisher’s Chi-square
A
1
vs. E 0,008 0,015
B
1
vs. E 0,002 0,004
C
1
vs. E 0,006 0,011
A
2
vs. E 0,177 0,162
B
2
vs. E 0,132 0,126
C
2
vs. E 0,165 0,154
In case of ‘normal’ versions of all algorithms the
results of classification are statistically significantly
different than the classification provided by the
expert. The closest classification is provided by
algorithm A with misclassified objects evenly
distributed over all classes. The worse performance
is observed in case of algorithm B characterised by
the largest percentage-wise differences between
accuracies of classification in different classes. In
case of ‘improved’ versions of considered
algorithms their performance is statistically
indifferent to the performance of the expert
considered as a ‘random’ decision-maker. It means
that for the sample of N=100 elements percentage of
misclassification of the order of 5% does not allow
us to decide which algorithm is statistically
significantly better than the other one. However
when we compare the respective p-values in this
case we will see the same pattern of behaviour as in
the case of the ‘normal’ versions of the considered
algorithms.
Now, let us apply the proposed methodology for
the comparison of ‘normal’ and ‘improved’ versions
of our hypothetical algorithms. The results of this
comparison are presented in Table 7.
Table 7: Comparison of different versions of algorithms.
Fisher’s Chi-square
A
1
vs. A
2
0,640 0,613
B
1
vs. B
2
0,470 0,446
C
1
vs. C
2
0,599 0,581
The results of this comparison are somewhat
unexpected for a non-statistician. Despite seemingly
large improvement (reduction of the percentage of
incorrect classifications from 10% to 5%) the
compared results statistically do not differ. The
reason for this behaviour is, of course, a small
sample size. What is also interesting that the
difference is the least significant (the highest p-value
in the test of equality) in the case of evenly
distributed misclassifications. The lowest p-value
(but still very high using statistical standards) is for
the case of algorithm B which assigns all incorrectly
classified objects to the class with the smallest
number of observations.
Finally, let us compare pair-wise ‘normal’ and
‘improved’ versions of our algorithms. The results
are presented in Table 8.
Table 8: Comparison of different algorithms.
Fisher’s Chi-square
A
1
vs. B
1
0,454 0,439
A
1
vs. C
1
0,918 0,906
B
1
vs. C
1
0,214 0,217
A
2
vs. B
2
0,908 0,901
A
2
vs. C
2
0,991 0,993
B
2
vs. C
2
0,801 0,807
Similarly to previously considered cases the
differences between performances of compared
algorithms are not statistically significant. This is
hardly unexpected as their accuracies are the same.
However, the type of the distribution of incorrectly
classified objects plays a visible role, especially in
the case of ‘normal’ (rather inaccurate) versions of
our algorithms.
Now, let us consider an example of the
application of this methodology to real data.
Suppose, that we have been provided with two
algorithms for the classification of vehicle
silhouettes data (data provided by Turing Institute,
Glasgow, and available at the UCI web-site). One of
these algorithms implements the Bayesian algorithm
POSSIBILISTIC METHODOLOGY FOR THE EVALUATION OF CLASSIFICATION ALGORITHMS
317

proposed in (Kulczycki and Kowalski, 2011), and
the second one implements a classical CRT
algorithm described in (Breiman et al., 1984). The
algorithms have been tested on two independent
samples, and the results of this comparison are
presented in Table 9.
Table 9: Comparison - Vehicle Silhouettes.
Alg.\Class 1 2 3 4 5
Bayes 55 48 112 90 141
CRT
46 55 86 84 175
The p-value obtained as the solution of (11) for
these data is equal to 0,079. According to the
classical statistical approach this result does not let
us claim that the Bayes algorithm is better than the
CRT. Note however, that similar results obtained on
the same sample would probably indicate the
superiority of the Bayes algorithm.
3 STATISTICAL EVALUATION
OF CLASSIFICATION
ALGORITHMS
In the previous section we proposed a simple
methodology for the statistical comparison of the
performance of different classification algorithms.
The results of classification obtained using
compared algorithms have been treated as random
samples. This assumption seems to be reasonable in
the case of evaluated algorithms but is somewhat
doubtful in case of the classification provided by an
expert. The other possible approach is to treat the
classification given by the expert as representing the
hypothetical ‘true’ distribution of observations
(
)
0
0
1
00
1
==
+KK
p,p,,p …
0
p
, and to verify the
hypothesis
0
11
00
110 ++
===
KKKK
pp,pp,,pp:H …
,
(12)
using the set of observed classification results
()
121 +
=
KK
n,n,,n,n …n
. To test this hypothesis we
may apply methodology of one-way contingency
tables.
Under the null hypothesis given by (12) the
observations are ruled by the multinomial
distribution
() ()
∏
+
=
+
=
1
1
0
11
K
i
n
i
K
i
p
nn
n
P
!!
!
n,p
0
,
(13)
Unfortunately, when we set
0
0
1
=
+K
p
we will
always reject the null hypothesis (12) when we will
observe even one misclassified object. Therefore we
have to set
0
0
1
>
+K
p
, and to modify the remaining
probabilities
00
1
K
p,,p …
in order to have their sum
equal to one. This operation can be interpreted as
allowing a certain (usually small) percentage of
incorrectly classified objects
0
1+
K
p
, and setting
allowable redistribution of this percentage among
considered classes.
The p-value for the exact test of the null
hypothesis (12) is equal to the sum of probabilities
of all possible observations
(
)
∗
+
∗∗∗∗
=
121 KK
n,n,,n,n …n
that are less probable than
observed vector
()
(
)
∑
∗
=−
Δ
0
pn ,Pvaluep
,
(14)
where
(
)
(
)
{
}
00
pnpnn ,P,P ≤=
∗∗
:
Δ
.
(15)
This test is computationally very demanding, and
can be used only in case of a few classes and rather
small number of observations. However, when the
total number of classified objects is sufficiently large
(>100), and there is more than five objects in each
class we can use asymptotic tests such as Pearson’s
chi-square goodness-of-fit test or Wald’s likelihood-
ratio LR test.
The test statistic for the Pearson’s chi-square
goodness-of-fit test is given by the formula
()
∑
+
=
−
=
1
1
0
2
0
2
K
i
i
ii
P
Np
Npn
χ
(16)
The p-value for this test is obtained by solving, with
respect to
p, the equation
2
1
2
p,KP −
=
χχ
,
(17)
where
2
1 p,K −
χ
is the quantile of order 1-p in the chi-
square distribution with
K degrees of freedom.
The test statistic for the likelihood-ratio test is
given by the following formula
()
ii
K
i
iR
pplnnL
0
1
1
2
∑
+
=
−=
,
(18)
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
318

where
Nnp
ii
=
. The p-value for this test is
obtained by solving, with respect to
p, the equation
2
1 p,KR
L
−
=
χ
,
(19)
where
2
1 p,K −
χ
is the quantile of order 1-p in the chi-
square distribution with
K degrees of freedom.
Asymptotically both these tests are equivalent.
However, for finite samples the
p-values of the
likelihood-ratio test are greater than the
p-values of
the Pearson’s goodness-of-fit test.
Let us apply the tests proposed in this section for
the evaluation of the algorithm B
2
. In this example
we will test two null hypotheses based on the results
of the classification given by the expert. In both
hypotheses we set the probabilities of first two
classes as equal to the probabilities estimated from
expert’s classification, i.e.
3020
0
2
0
1
,p,,p ==
. In the
first of the considered hypotheses we allow 1% of
incorrectly classified objects in the third class, i.e.
010490
0
4
0
3
,p,,p ==
, and in the second hypothesis
we allow greater, equal to 2%, percentage of
incorrectly classified objects in the third class, i.e.
020480
0
4
0
3
,p,,p ==
. The results of the tests are
given in Table 10.
Table 10: Evaluation of algorithm B
2
.
Hypothesis Exact
Chi-
square
Likelihood
- ratio
010
0
4
,p =
0,0011 0,0006 0,023
020
0
4
,p =
0,132 0,120 0,202
We see that the performance of algorithm B
2
is
statistically different from the performance
represented by the first tested hypothesis. However,
if we relax the requirement on the percentage of
incorrectly classified objects, as it is in the case of
the second hypothesis, the differences are
statistically insignificant (using traditional statistical
criteria of significance). One has to note the
difference between these results and the results of
comparison presented in the previous section. When
we treated expert’s classification as a random
sample, the differences were statistically
insignificant. However, when we use expert’s results
as representing somewhat relaxed, but true, class
probabilities, the first test shows statistically
significant difference (lack of fit). Thus, the tests
proposed in this section are more demanding when
we evaluate the performance of classification
algorithms.
4 POSSIBILISTIC EVALUATION
OF TEST RESULTS
In the previous sections we have proposed statistical
tests for the evaluation of classification procedures.
The results of the proposed test procedures have
been expressed in terms of significance, known also
as the test volume or the
p-value. Examples given in
these sections show that in many cases it is difficult
to obtain statistically significant results supporting
the hypothesis that e.g. one classification algorithm
is better than the other one. Therefore, there is a
need to present an additional indicator that can be
used to show to what extent one algorithm is better
than the other one despite the fact that they are
statistically equivalent. This goal can be achieved
using the methodology proposed in the
theory of
possibility
. In order to do so we need to have an
interpretation of the
p-value in terms of the
possibility theory, as it was proposed in
(Hryniewicz, 2000) and (Hryniewicz, 2006). This
interpretation gives a decision maker the evaluation
of test’s result using notions of
possibility or
necessity of making certain decisions.
In the previous sections the statistical decision
problem is described by setting the null hypothesis
H
0
. In order to make correct decisions we have to set
an alternative hypothesis
K. In the context of
decision-making we usually choose this hypothesis
which is better supported by statistical evidence.
Now, let us consider these two hypotheses,
separately. First, let us analyze the null hypothesis
H
0
whose significance is given by the p-value equal
to
p
H
. The value of p
H
shows to what extent the
statistical evidence supports the null hypothesis.
When this value is relatively large we may say that
H
0
is strongly supported by the observed data.
Otherwise, we should say that the data do not
sufficiently support
H
0
. It is worthwhile to note that
in the latter case we do not claim that the data
support the alternative hypothesis
K. The same can
be done for the alternative hypothesis
K. The
statistical test of this hypothesis may be described by
another
p-value denoted by p
K
. When K= not H
0
we
have
p
K
=1-p
H
. However, in a general setting this
equality usually does not hold.
In (Hryniewicz, 2006) it was proposed to evaluate
the null hypothesis
H
0
by a fuzzy set
H
~
with the
following membership function
POSSIBILISTIC METHODOLOGY FOR THE EVALUATION OF CLASSIFICATION ALGORITHMS
319

()
[]
()
[]
⎩
⎨
⎧
=−
=
=
1121
021
xp,min
xp,min
x
H
H
H
μ
.
(20)
This membership function may be interpreted as a
possibility distribution of H
0
. If
()
11 =
H
μ
holds it
means that it is quite
plausible that the considered
hypothesis is not true. On the other hand, when
()
10 =
H
μ
, we would not be surprised if H
0
were
true. One has to note, that the values
()
x
H
μ
do not
have interpretation in terms of probabilities, but
represent the possibilities of the correctness of the
considered decisions. These possibilities can be
interpreted, however, as upper probabilities in the
theory of imprecise probability.
The same can be done for the alternative
hypothesis
K. The alternative hypothesis K is now
represented by a fuzzy set
K
~
with the following
membership function
()
[]
()
[]
⎩
⎨
⎧
=−
=
=
1121
021
xp,min
xp,min
x
K
K
K
μ
.
(21)
In order to choose an appropriate decision, i.e. to
choose either
H
0
or K it has been proposed in
(Hryniewicz, 2006) to use three measures of
possibility defined by (Dubois and Prade, 1983).
First measure proposed by these authors is
named the
Possibility of Dominance (PD). For two
fuzzy sets
A
~
and
B
~
, described by their membership
functions
()
x
A
μ
and
()
y
B
μ
, respectively, this
index is defined in (Dubois and Prade, 1983) in the
following way
(
)
() ()
[]
y,xminsupB
~
A
~
PD
BA
yxy,x
μμ
≥
=≥
:
.
(22)
The value of PD represents the possibility that the
fuzzy set
A
~
is not dominated by the fuzzy set
B
~
.
The second index is called the
Possibility of
Strict Dominance
(PSD), and for two fuzzy sets
A
~
and
B
~
is given by the expression
()
() ()()
[]
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
−=>
≤
y,xmininfsupB
~
A
~
PSD
BA
yxyx
μμ
1
:
(23)
Positive, but smaller than 1, values of this index
indicate certain weak evidence that
A
~
strictly
dominates
B
~
.
Third measure is named the
Necessity of Strict
Dominance
, and for two fuzzy sets
A
~
and
B
~
has
been defined in (Dubois and Prade, 1983) as
(
)
() ()()
[]
y,xminsupB
~
A
~
NSD
BA
yxy,x
μμ
≤
−=>
:
1
.
(24)
The
NSD index represents a necessity that the fuzzy
set
A
~
strictly dominates the set
B
~
.
In the considered statistical problem of testing a
hypothesis
H
0
against an alternative K these indices
have been calculated in (Hryniewicz, 2006), and are
given by the following formulae
()
() ()
[]
10
KH
,maxK
~
H
~
PD
μμ
=≥
,
(25)
()
() ()
[]
010
KH
,minK
~
H
~
PSD
μμ
−=>
,
(26)
()
() ( )
[]
011
KH
,maxK
~
H
~
NSD
μμ
−=>
.
(27)
The value of PD represents the possibility that
according to the observed statistical data the choice
of the null hypothesis is not a worse decision than
choosing its alternative. The value of PSD gives the
measure of possibility that the data support rather the
null hypothesis than its alternative. Finally, the value
of NSD gives the measure of necessity that the data
support the null hypothesis rather than its
alternative.
Close examinations of the proposed measures
reveals that
NSDPSDPD ≥≥ .
(28)
Therefore, it means that according to the practical
situation we can choose the appropriate measure of
the correctness of our decision. If the choice
between H
0
and K leads to serious consequences we
should choose the NSD measure. In such a case
p
H
>0,5 is required to have NSD>0. When these
consequences are not so serious we may choose the
PSD measure. In that case PSD>0 when p
K
<0,5, i.e.
when there is no strong evidence that the alternative
hypothesis is true. Finally, the PD measure, which is
always positive, gives us the information of the
possibility that choosing H
0
over K is not a
completely wrong decision.
In the cases considered in this paper the
alternative hypothesis has been usually formulated
as the complement of the null hypothesis, Thus, we
have the equality p
K
=1-p
H
. It is easy to show that in
such a case we have
()
() ( )
HH
p,minK
~
H
~
PD 210 ==≥
μ
,
(29)
() ()
()
[]
H
p,minK
~
H
~
NSDK
~
H
~
PSD −−=>=> 1211
.
(30)
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
320
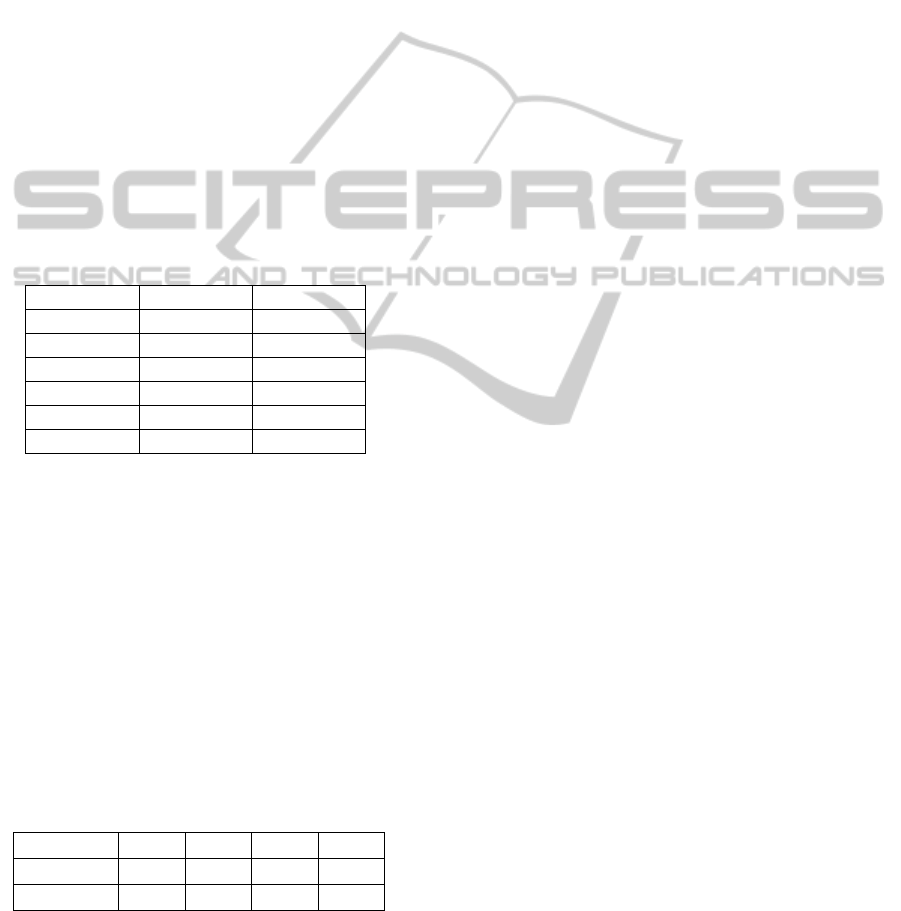
Let us apply these results for the comparison of
different algorithms using the test results presented
in Table 7 for Fisher’s exact test. The results of the
comparison are presented in Table 11.
From the analysis of this table we see that the
statistical evidence is not strong enough to claim that
algorithm A
1
is necessarily equivalent to algorithm
B
1
. This evidence is even weaker if we claim the
equivalence of algorithms B
1
and C
1
. In all other
cases the evidence is very strong that the considered
algorithms are equivalent. It is worthy to note, that
by using classical statistical interpretation in all
considered cases we would not reject the hypothesis
of the equivalence of compared algorithms.
The possiblilistic comparisons are not necessary
when null and alternative hypotheses are, as in the
particular cases considered in this paper,
complementary. In such case strong evidence in
favour of the null hypothesis means automatically
weak support of its complementary alternative.
Table 11: Possibilistic comparison of different algorithms.
PD PSD,NSD
A
1
vs. B
1
0,908 0
A
1
vs. C
1
1 0,836
B
1
vs. C
1
0,428 0
A
2
vs. B
2
1 0,816
A
2
vs. C
2
1 0,982
B
2
vs. C
2
1 0,602
In general, it must not be the case. Consider, for
example, a test of the equivalence of a new
classification algorithm against two alternatives
representing known results of the usage of other
algorithms. We want to know which of those
algorithms our new algorithm is similar to with
respect to its efficiency. Consider, for example, the
problem of the classification of wheat kernels
described in (Charytanowicz et al., 2010). Two
algorithms, namely QDA and CRT, have been used
on large samples of data. The results of those
experiments have been used for the estimation of
class probabilities. They are presented in Table 12.
Table 12: Wheat kernels - probabilities of classes.
Alg.\Class 1 2 3 4
QDA 0,319 0,310 0,314 0,057
CRT
0,300 0,324 0,310 0,066
Test results for a new algorithm are described by
the following vector (29, 29, 32, 15). The
comparison of this result with probabilities obtained
by the QDA algorithm, performed according to the
methodology presented in the third section, gives a
very small p-value equal to 0,002. Similar
comparison with the probabilities obtained by the
CRT algorithm yield also a very small p-value equal
to 0,018. Using (25) - (27) we can calculate
possibilistic indices showing that our algorithm is
more closer to the CRT algorithm than to the QDA
algorithm. The results are the following: PD=1,
PSD=0,036, NSD=0. The necessity measure that the
new algorithm is more similar to the CRT than to
QDA is equal to zero. Thus, the obtained statistical
data do not let us to exclude that our algorithm is
more similar to the QDA than to the CRT. However,
the possibility indices show that it fully possible
(PD=1) that the efficiency of the new algorithm is
similar to the efficiency of both other algorithms, but
it is only slightly possible (PSD=0,036) that the new
algorithm is more similar to the CRT than to the
QDA.
The applicability of the proposed possibilistic
measures is even much stronger when we omit the
assumption that the ‘expert’ indicates only one ‘true’
class. This is always the case when the role of ‘an
expert’ is played by a fuzzy clustering algorithm. In
all such cases we have to use the methodology of
fuzzy statistics, whose overview can be found e.g. in
(Gil and Hryniewicz, 2009).
5 CONCLUSIONS
In the paper we have considered the problem of the
evaluation and comparison of different classification
algorithms. For this purpose we have applied the
methodology of statistical tests for the multinomial
distribution. We restricted our attention to the case
of the supervised classification when an external
‘expert’ evaluates the correctness of classification.
The results of the proposed statistical tests are
interpreted using the possibilistic approach
introduced in (Hryniewicz, 2006). This approach
will be more useful or even indispensable when we
assume more complicated statistical tests and
imprecise statistical data. We will face such
problems when we will adapt the methodology
presented in this paper for the case of fuzzy
classifiers.
The future development of the proposed
methodology should be concentrated on two general
problems. First, we should compare the results of
classification with ‘better’ alternatives. The meaning
of the word ‘better’ in the considered context
requires further investigations. The same can be said
in case fuzzy classifiers built using supervised and
POSSIBILISTIC METHODOLOGY FOR THE EVALUATION OF CLASSIFICATION ALGORITHMS
321

unsupervised learning procedures.
ACKNOWLEDGEMENTS
The author expresses his thanks to Dr. P.A.
Kowalski for providing solutions for some practical
examples of classification problems.
REFERENCES
Agresti, A., 2006. Categorical Data Analysis. J. Wiley,
Hoboken, N J, 2
nd
edition.
Berthold, M., Hand, D. J. (Eds.), 2007. Intelligent Data
Analysis. An Introduction, Springer, Berlin, 2
nd
edition.
Breiman, L., Friedman, J., Olshen, R, Stone, C., 1984.
Classification and Regression Trees, CRC Press, Boca
Raton, FL.
Charytanowicz, M., Niewczas J., Kulczycki, P., Kowalski,
P. A., Łukasik, S. Żak, S., 2010. A Complete Gradient
Clustering Algorithm for Features Analysis of X-ray
Images". In: Information Technologies in Biomedicine,
E. Pietka, E. Kawa (Eds.), Springer-Verlag, Berlin-
Heidelberg, 2010, 15-24.
Desu, M. M., Raghavarao, D., 2004. Nonparametric
Statistical Methods for Complete and Censored Data,
Chapman & Hall, Boca Raton, FL.
Dubois D., Prade, H., 1983. Ranking Fuzzy Numbers in
the Setting of Possibility Theory. Information Science
30, 183-224.
Gil, M. A., Hryniewicz, O., 2009. Statistics with Imprecise
Data. In: Robert A. Meyers (Ed.): Encyclopedia of
Complexity and Systems Science. Springer,
Heidelberg, 8679-8690.
Hryniewicz, O., 2000. Possibilistic Interpretation of the
Results of Statistical Tests. Proceedings of Eight
International Conference on Information Processing
and Management of Uncertainty in Knowledge-based
Systems IPMU 2000, Madrid, 215-219.
Hryniewicz, O., 2006. Possibilistic decisions and fuzzy
statistical tests. Fuzzy Sets and Systems, 157, 2665-
2673
Krzanowski, W. J., 1988. Principles of Multivariate
Analysis: A User's Perspective. Oxford University
Press, New York.
Kulczycki, P., Kowalski, P.A., 2011. Bayes classification
of imprecise information of interval type. Control and
Cybernetics 40 (in print)
Nisbet, R., Elder, J., Miner, G., 2009. Statistical Analysis
and Data Mining. Applications, Elsevier Inc,
Amsterdam.
ICSOFT 2011 - 6th International Conference on Software and Data Technologies
322
