
ON THE (NON-)REUSABILITY OF FUZZY SKETCHES
AND EXTRACTORS AND SECURITY IN THE COMPUTATIONAL
SETTING
∗
Marina Blanton and Mehrdad Aliasgari
Department of Computer Science and Engineering, University of Notre Dame, Notre Dame, U.S.A.
Keywords:
Biometrics, Fuzzy sketches and extractors, Reusability, Computational setting.
Abstract:
Secure sketches and fuzzy extractors enable the use of biometric data in cryptographic applications by correct-
ing errors in noisy biometric readings and producing cryptographic materials suitable for many applications.
Such constructions work by producing a public sketch, which is later used to reproduce the original biometric
and all derived information exactly from a noisy biometric reading. It has been previously shown that release
of multiple sketches associated with a single biometric presents security problems for certain constructions.
Through novel analysis we demonstrate that all other constructions in the literature are also prone to similar
problems, which hinders their adoption in practice. To mitigate the problem, we propose for each user to
store one short secret string for all possible uses of her biometric, and show that simple constructions in the
computational setting have numerous security and usability advantages under standard hardness assumptions.
Our constructions are generic in that they can be used with any existing secure sketch as a black box.
1 INTRODUCTION
The motivation for this work comes from practical use
of biometric-derived data and its suitability for adop-
tion. Secure sketches and fuzzy extractors (Dodis
et al., 2004) were introduced as mechanisms of deriv-
ing cryptographic material from noisy biometric data,
which can be used for authentication, encryption, and
other purposes. Such constructions produce a helper
string (secure sketch) – which is viewed as public
– from a biometric and later re-produce the crypto-
graphic string from a close noisy biometric reading
using the helper string. Only minimal information
about the biometric should be leaked due to the re-
lease of the helper string.
While this powerful concept enables new applica-
tions and can be attractiveto users who no longer need
to maintain secrets to participate in cryptographicpro-
tocols, it has been shown that leakage of informa-
tion associated with the biometric in such construc-
tions is unavoidable (Smith, 2004; Dodis and Smith,
2005). Furthermore, this concept has been more heav-
ily studied in the context when the construction is ap-
plied to a biometric only once. Consecutive publica-
∗
This work was partially supported by grant FA9550-
09-1-0223 from the Air Force Office of Scientific Research.
tions (Boyen, 2004; Simoens et al., 2009) explored
the security guarantees of such schemes in terms of
their reusability, when a single biometric or its noisy
version is used to produce multiple secure sketches
using the same or different algorithms. Informa-
tion leakage prevents such constructions from meet-
ing standard security requirements sought of them in
cryptographic applications such as indistinguishabil-
ity (inability to link two records to the same biomet-
ric) and irreversibility (inability to reverse the con-
struction and directly recover information about the
biometric). Some of the more popular constructions
have been shown to have serious security weaknesses
in presence of even very weak adversaries (Simoens
et al., 2009). In this work, we analyze other schemes
from the literature and show that they also cannot be
safely reused. In particular, our novel analysis shows
that the remaining constructions fail to satisfy stan-
dard security expectations with respect to reusability
and therefore cannot be used in security applications.
In such schemes, information leakage is quanti-
fied as the entropy loss associated with the release
of the helper string, providing a rough upper bound.
For the current error rates and typical sets of parame-
ters in biometric data, the information theoretic anal-
ysis provides bounds that result in leakage of most or
68
Blanton M. and Aliasgari M..
ON THE (NON-)REUSABILITY OF FUZZY SKETCHES AND EXTRACTORS AND SECURITY IN THE COMPUTATIONAL SETTING.
DOI: 10.5220/0003454900680077
In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2011), pages 68-77
ISBN: 978-989-8425-71-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

even all entropy contained in a biometric (see (Blan-
ton and Hudelson, 2009) for a sample iris code analy-
sis). Because this information leakage is unavoidable,
it presents problems even in case of weak adversaries.
To overcome the issues of information leakage
and unsafe reuse of biometrics, we propose to use the
computationalsetting, where a user stores a single key
and the adversary is computationally bounded. The
key is introduced for the purpose of avoiding informa-
tion leakage and improving security of the schemes
and does not change the functionality. We believe
that keeping a single short key for all possible uses of
biometric-based material in different security applica-
tions is a small price to pay for achieving significant
security improvements (which otherwise are not pos-
sible) and the ability to safely use such constructions
in a variety of applications. We show that the use of
one key and standard computational assumptions (ex-
istence of pseudo-random and hash functions) is suf-
ficient for achieving very attractive properties using
simple schemes. Our constructions are generic in that
they can use any existing secure sketch scheme as a
black box for any type of distance metric).
We would like to note that the use of the secret in
our schemes should not be confused with multi-factor
authentication or the use of shared secrets, as in our
schemes the secret never leaves the user and is not
shared and a single secret is sufficient for all possi-
ble uses including multiple biometric types, multiple
applications, and multiple servers.
The security benefits of our schemes are:
• We achieve provably no information leakage.
• Previously, only certain restricted types of error-
correcting codes could be used to ensure security
of fuzzy sketches and extractors (Boyen, 2004).
Our solution lifts such restrictions and can be used
with any type of error-correcting code.
• Prior (Simoens et al., 2009) and our analysis of
secure sketch constructions shows that they all
fail to achieve standard security requirements for
cryptographic applications, while our solution is
secure in a much stronger adversarial model.
• Previously, exposure of a biometric-derived key
was shown to reveal no information about the bio-
metric for a specific construction in the random
oracle model (Boyen, 2004). Our construction, on
the other hand, achieves this result in the standard
model using any existing secure sketch.
In our analysis of existing constructions, we use
a very weak adversary. The security of our own
schemes, on the other hand, is shown using a very
strong adversary (the strongest in the literature).
To summarize, our contributions are two-fold: (i)
new analysis of fuzzy sketch schemes that shows that
even a weak adversary has a significant advantage in
compromising security of existing constructions, and
(ii) simple schemes that use a single secret to achieve
strong security under standard assumptions.
2 MODEL AND DEFINITIONS
2.1 Fuzzy Sketches and Extractors
Secure (or fuzzy) sketches, introduced by (Dodis et al.,
2004), correct errors in noisy secrets by releasing a
helper string S. Let W denote a random variable and
w its value.
Definition 1. A (M ,m,m
′
,t)-secure sketch is a pair
of randomized algorithms:
• SS is a function that, on input w from metric space
M with distance function dist, outputs a sketch S.
• Rec is a function that, on input w
′
∈ M and
S = SS(w), recovers and outputs the original w
if dist(w, w
′
) ≤ t.
Secure sketches have been constructed for different
metric spaces M , for which dist(a,b) is defined for
all a, b ∈ M . Security of a secure sketch is evaluated
in terms of entropy of W before (m) and after (m
′
)
releasing the string S, i.e., the entropy loss m− m
′
as-
sociated with making S public. Precise definitions can
be found in (Dodis et al., 2008).
Fuzzy extractors allow one to extract randomness
from w (to use it as cryptographic material) and later
reproduce it using w
′
close to the original w.
Definition 2. A (M , m, m
′
,t,ε)-fuzzy extractor is a
pair of algorithms:
• Gen is a function that, on input w ∈ M , outputs
extracted random string R and a helper string P.
• Rep is a function that, on input w
′
and P repro-
duces and outputs R that was generated using
Gen(w) if dist(w,w
′
) ≤ t.
The security requirement is that, for any W of min-
entropy m, the statistical distance between the distri-
bution of R and the uniform distribution of strings of
the same length is no greater than ε, even after ob-
serving P. A fuzzy extractor can be built from a se-
cure sketch using a generic construction from (Dodis
et al., 2004):
Gen(w):
1. Execute S ← SS(w;r
1
), where r
1
denotes random
coins used by SS (if any).
2. Use a strong extractor Ext to extract a random
string R from w, i.e., R ← Ext(w;r
2
), where r
2
denotes random coins used by Ext.
3. Output public P = (S,r
2
) and secret R.
ON THE (NON-)REUSABILITY OF FUZZY SKETCHES AND EXTRACTORS AND SECURITY IN THE
COMPUTATIONAL SETTING
69

Rep(w
′
,P = (S, r
2
)):
1. Execute w ← Rec(w
′
,S). If Rec fails (i.e., when
dist(w,w
′
) > t such that S = SS(w)), stop.
2. Extract R from w using r
2
as R ← Ext(w,r
2
) and
output R.
Strong extractors (Nisan and Ta-Shma, 1999) can ex-
tract at most m − 2log(
1
ε
) + O(1) nearly random bits
(m and ε are as defined above). The entropy loss of
2log(
1
ε
) + O(1) is in addition to the loss due to re-
lease of sketch S, unless the extractor is modeled as a
random oracle.
Many constructions utilize error-correcting codes.
A code C is a subset of K elements {w
0
,. . .,w
K−1
} of
M . The minimum distance of C is the smallest d such
that dist(w
i
,w
j
) ≥ d for all i 6= j, which implies that
the code can detect up to d − 1 errors; and the error-
correcting distance is t = ⌊(d − 1)/2⌋. A linear error-
correcting code C over field F
q
is a k-dimensional lin-
ear subspace of the vector space F
n
q
which uses Ham-
ming distance as the metric. For any linear code C, an
(n− k) × n parity-check matrix H projects any vector
v ∈ F
n
q
to the space orthogonal to C. This projection
is called the syndrome and denoted by syn(v) = Hv.
Then v ∈ C iff syn(v) = 0. The syndrome contains all
information necessary for decoding, i.e., when code-
word c is transmitted and noisy w = c+ e is received,
syn(w) = syn(c) + syn(e) = 0+ syn(e), where syn(e)
can be used to determine the error pattern e.
Metric-specific secure sketch constructions are
known for the Hamming distance (used for iris
codes), the set difference (used for fingerprints), and
the edit distance (used for DNA comparisons). Also,
the permutation-based construction is available for
any transitive metric (e.g., Hamming distance and
set intersection). Schemes for the Hamming distance
have been most heavily analyzed, and some schemes
are known to have security problems when reused on
related biometrics. In this work we analyze remaining
known constructions and show their insecurity.
2.2 Secure Sketch Constructions
(Simoens et al., 2009) show that two popular secure
sketch constructions – the code offset construction
with a linear error-correctingcode (the syndrome con-
struction) and the construction based on permutation
groups – do not withstand the requirements of indis-
tinguishability and reversibility, i.e., the adversary can
win such experiments with overwhelming probability.
The former scheme is for the Hamming distance (and
is among the most widely studied schemes) and the
latter is for any transitive distance metric. We con-
centrate on the analysis of other schemes and outline
schemes for the set difference and edit distance. In
what follows, we use a
R
← A to denote that the value a
is chosen uniformly at random from the set A.
Fuzzy Vault. The fuzzy vault scheme (Juels and
Sudan, 2002) can be used as a fuzzy sketch for set
difference. A biometric is comprised of unordered
elements w = {w
1
,. . .,w
s
} (e.g., minutiae points in
fingerprints), which are disguised by adding a large
number of chaff points. The genuine points carry
information that allows w to be reconstructed from
noisy w
′
. Here t ∈ [1,s] and r ∈ [s+ 1,n] are system-
wide parameters, where n is the set of all possible
points, or the universe. Work is over field F
n
, where n
is a prime power.
To compute SS(w):
1. Choose a random polynomial p(·) of degree at
most s− t − 1 over F
n
.
2. For each w
i
∈ w, let x
i
= w
i
and y
i
= p(x
i
).
3. Choose r− s distinct points x
s+1
,. . .,x
r
at random
from F
n
\ w and set y
i
R
← F
n
\ {p(x
i
)} for i = s+
1,...,r.
4. Output SS(w) = {(x
1
,y
1
),. . .,(x
s
,y
s
)} sorted by
the value of x
i
’s.
To compute Rec(w
′
,S):
1. Create the set D of pairs (x
i
,y
i
) such that x
i
∈ w
′
.
2. Run Reed-Solomon decoding on D to recover the
polynomial p(·).
3. Output s points of the form (x
i
, p(x
i
)) from S.
Privacy of the biometric depends on the number and
distribution of points S (i.e., the difficulty of identi-
fying the original points and the number of spurious
polynomials created by the chaff points). The en-
tropy loss due to the release of S is upper bounded
by tlogn+ log
n
r
− log
n−s
r−s
+ 2.
Improved Fuzzy Vault. (Dodis et al., 2008)observed
that the polynomial in the above construction does not
need to be random, which allows for a secure sketch
with significantly lower entropy loss, t logn.
To compute SS(w):
1. Compute unique monic polynomial p(x) =
∏
w
i
∈w
(x− w
i
) of degree s.
2. Output the coefficientsof p() of degree s−1 down
to s− t, which will form SS(w) = (c
s−1
,. . ., c
s−t
).
To compute Rec(w
′
,S = (c
s−1
,. . .,c
s−t
)):
1. Create a new polynomial p
high
of degree s that
shares the top t + 1 coefficients with p(), i.e.,
p
high
(x) = x
s
+
∑
s−1
i=s−t
c
i
x
i
.
2. Evaluate p
high
on points of w
′
to obtain pairs
(a
1
,b
1
), ..., (a
s
,b
s
).
3. Use Reed-Solomon decoding to find a polynomial
p
low
of degree s− t − 1 such that p
low
(a
i
) = b
i
for
at least s− t/2 values of a
i
’s. If none are found,
output fail.
4. Output the roots of the polynomial p
high
− p
low
.
SECRYPT 2011 - International Conference on Security and Cryptography
70

Another construction for set difference, Pinsketch,
is suitable for large universe sizes and variable num-
ber of elements in w. It is syndrome-based, and its
(in)security is not difficult to reduce to the previously
analyzed code-offset scheme. We thus omit its anal-
ysis. For the edit distance, the only known way to
construct a secure sketch is by embedding it into a
transitive metric of larger dimension and applying a
secure sketch construction to the target metric. An
embedding with attractive properties was developed
in (Dodis et al., 2008) using Pinsketch. Once again,
the insecurity of the resulting scheme can be shown
using prior results and is omitted. This covers all se-
cure sketch schemes.
2.3 Security Notions
The original security definitions of fuzzy sketches and
extractors were formulated for a single instance of a
fuzzy sketch or extractor in isolation (Dodis et al.,
2004). Consecutive literature (Boyen, 2004; Simoens
et al., 2009) considered a stronger (and more re-
alistic) adversarial model where such constructions
can be invoked multiple times and therefore the se-
curity guarantees must hold when the constructions
are reused. Furthermore, the power granted to the
adversary can greatly differ. In this work we use
weak adversaries while analyzing existing construc-
tion (to show that they do not provide sufficient secu-
rity guarantees even in presence of weak adversaries)
and strong adversaries when proving security of our
proposed solution. In a nutshell, a weak adversary
is given two fuzzy sketches and tries to determine
whether they were produced using related biometrics
or what the biometric was, while a strong adversary
can adaptively ask for fuzzy sketches and private keys
that fuzzy extractors output.
Let t be the maximum amount of errors that the
biometric system can tolerate. We define ∆
t
to be the
set of all perturbation functions that represent differ-
ences in sampling biometric data; we get ∆
t
= {δ :
M → M such that dist(w, δ(w)) ≤ t}. We next de-
fine a security game for weak adversaries with access
to public sketches and then proceed with a security
game for strong adversaries. Two security properties
for weak adversaries were defined in (Simoens et al.,
2009): sketch indistinguishability and irreversibility.
2-Indistinguishability Game. (Simoens et al.,
2009):
1. The challenger chooses a random variableW ∈ M
and samples it to obtain w
1
∈ M . The challenger
computes S
1
= SS(w
1
) and gives S
1
to A .
2. The challenger chooses b
R
← {0,1}. If b = 1, the
challenger chooses δ
R
← ∆
t
and produces related
w
2
= δ(w
1
). Otherwise, the challenger samplesW
to obtain a different w
2
. The challenger computes
S
2
= SS(w
2
) and gives S
2
to A .
3. The adversary A eventually produces a bit b
′
and
wins if b
′
= b.
A ’s advantage in this game is defined as Adv
ind
A
=
2
Pr[b
′
= b] −
1
2
= 2
Pr[b
′
6= b] −
1
2
.
Definition 3. An (M ,m,m
′
,t)-secure fuzzy sketch
(SS, Rec) is ε-indistinguishable in ∆
t
if for any ad-
versary A it holds that Adv
ind
A
≤ ε. The fuzzy sketch is
reusable when ε is negligible.
The irreversibility property of a fuzzy sketch scheme
means that an adversary who obtains access to multi-
ple sketches generated from the same noisy input us-
ing possibly different sketching functions is unable to
recover the original input. In the current version of
this work we do not treat irreversibility, since a fail-
ure to achieve the indistinguishability property alone
points out weaknesses of a fuzzy sketch scheme.
We now proceed with defining security games for
more powerful adversaries using what we term weak
biometric privacy and strong biometric privacy. In
both of them the adversary is allowed to query the
scheme a large number of times, but the difference is
that in the first the adversary obtains access only to the
public information, while in the second it also obtains
access to the key output by a fuzzy extractor. Thus,
we use the first definition for secure sketches and the
second one for fuzzy extractors.
The two security games below are roughly equiva-
lent to outsider and insider chosen perturbation secu-
rity in (Boyen, 2004), but are stronger than the respec-
tive definitions in (Boyen, 2004). In particular, in our
definition of weak biometric security we require the
adversary to only distinguish between two sketches,
while the adversary was required to recover the bio-
metric w in (Boyen, 2004). Furthermore, instead of
allowing the adversary to query fuzzy sketches for a
particular biometric w and then challenging the ad-
versary by asking it to distinguish between a sketch
for w and a sketch for a randomly chosen biometric,
we setup two biometrics w
0
and w
1
and allow the ad-
versary to query sketches for both. Then during the
challenge, the adversary is asked to determine which
biometric was used in producing the challenge sketch.
This can give the adversary advantage over the prior
formulation, especially in the computational setting
where different users will possess different keys.
As our schemes work in the computational setting,
we use κ to denote the security parameter. All algo-
rithms are assumed to be polynomial time in κ. Then
a function ε(κ) is negligible if for all positive polyno-
mials p(·) and sufficiently large κ ε(κ) < 1/p(κ).
ON THE (NON-)REUSABILITY OF FUZZY SKETCHES AND EXTRACTORS AND SECURITY IN THE
COMPUTATIONAL SETTING
71

Weak Biometric Privacy.
1. (Preparation) A chooses a random variable W ∈
M and sends its specification to the challenger.
2. (Sampling) The challenger randomly samples W
to obtain w
0
∈ M and w
1
∈ M and initializes two
users U
0
and U
1
, resp., using that information.
3. (Queries) A makes up to q possibly adaptive
sketching queries: to form query i, A chooses
δ
i
∈ ∆
t
and sends it and a bit b
i
to the challenger.
The challenger computes S
i
← SS(δ
i
(w
b
i
);r
i
) us-
ing fresh randomness r
i
and returns S
i
to A .
4. (Challenge) The challenger chooses a bit b
R
←
{0,1} and δ
R
← ∆
t
, and produces a biometric
w
′
= δ(w
b
). The challenger then computes S ←
SS(w
′
;r) using fresh random r and gives S to A .
5. (More queries) A can run more queries up to the
bound q as specified in step 3.
6. (Response) A eventually produces a bit b
′
and
wins if b
′
= b.
A ’s advantage in this game is defined as Adv
wbp
A
(κ) =
2
Pr[b
′
= b] −
1
2
= 2
Pr[b
′
6= b] −
1
2
.
Definition 4. An (M ,m,m
′
,t)-secure fuzzy sketch
(SS, Rec) has weak biometric privacy if for any prob-
abilistic polynomial-time (PPT) adversary A it holds
that Adv
wbp
A
(κ) ≤ ε(κ) for a negligibly small ε(κ).
Note that unlike previous definitions, we explicitly
specify the security parameter κ and define the ad-
versary’s advantage as a function of it.
The next definition corresponds to the strongest
version of the insider chosen perturbation security
definition in (Boyen, 2004). The adversary can query
the challenger to obtain sketches on both related and
unrelated biometrics and private key corresponding to
unrelated biometrics. This time we ask the adver-
sary to distinguish between the secret key output by
a fuzzy extractor on a related biometric and a ran-
domly chosen string. Note that we do not ask the ad-
versary to distinguish between biometric-derivedkeys
of two users because the adversary has the choice of
the sketch that it can use in the challenge. This means
that the adversary will trivially know for which user
the secret key will be produced. We, however, note
that in order to distinguish secret keys corresponding
to two users, the adversary need to be able to distin-
guish at least one of them from a random string. Thus,
our definition of security will imply the security in
the game with two users. Let ∆ denote all perturba-
tion functions over space M , i.e., ∆ = {δ : M → M }
where dist(w,δ(w)) can be greater than t.
Strong Biometric Privacy.
1. (Preparation) A chooses W ∈ M and gives its
specification to the challenger.
2. (Sampling) The challenger randomly samples W
to obtain w ∈ M .
3. (Public queries) A makes up to q possibly adap-
tive generation queries: to form query i, A
chooses δ
i
∈ ∆ and sends it to the challenger. The
challenger computes (P
i
,R
i
) ← Gen(δ
i
(w);r
i
) us-
ing fresh random r
i
and returns public P
i
to A .
4. (Private queries) A makes up to q
′
possibly adap-
tive reproduction queries that can be interspersed
with public queries as follows: to form query i,
A chooses δ
′
i
∈ ∆ and a public data P
′
i
and sends
them to the challenger. The challenger computes
R
′
i
← Rep(δ
′
i
(w);P
′
i
) and returns R
′
i
to A .
5. (Challenge) A chooses string P
∗
∈ {P
1
,. . .,P
q
}
from one of the strings returned by the challenger
in a public query such that P
∗
was produced using
a public query δ
i
with dist(w,δ
i
(w)) ≤ t and in any
private query (δ
′
i
,P
∗
) the distance dist(w,δ
′
i
(w)) >
t. A sends P
∗
to the challenger. The challenger
chooses a bit b
R
← {0,1}. If b = 1, the challenger
computes R ← Rep(w, P
∗
) and gives it to A . Oth-
erwise, if b = 0, it chooses a random string of the
same length and gives it to A instead.
6. (More queries) A can run additional queries as
specified in steps 3 and 4 (up to q and q
′
queries,
respectively) with the exception that any query
(δ,P
∗
) such that dist(w,δ(w)) ≤ t is not allowed.
7. (Response) A eventually produces a bit b
′
and
wins if b
′
= b.
A ’s advantage in this game is defined as Adv
sbp
A
(κ) =
2
Pr[b
′
= b] −
1
2
= 2
Pr[b
′
6= b] −
1
2
.
Definition 5. We say that an (M ,m,m
′
,t,ε)-secure
fuzzy extractor (Gen, Rep) has strong biometric pri-
vacy if for any PPT adversary A it holds that
Adv
sbp
A
(κ) ≤ ε(κ) for a negligibly small ε(κ).
3 ANALYSIS OF EXISTING
SCHEMES
Fuzzy Vault. Before proceeding with the analysis,
we note that the basic idea for the strategy in attacking
the fuzzy vault scheme when two or more sketches are
available – computing the intersection of the points
– is straightforward and is not new. This attack ap-
peared in (Scheirer and Boult, 2007; Kholmatov and
Yanikoglu, 2008; Poon and Miri, 2009). We still an-
alyze the construction here because all previous pub-
lications assume that given sketches are related and
proceed with identifying original points. Our work,
however, assumes a significantly weaker (and perhaps
more realistic) adversary that would like to determine
if two given sketches are related or not, which is a
SECRYPT 2011 - International Conference on Security and Cryptography
72

much more difficult task. Therefore, we present a
rigorous new analysis that shows weaknesses of the
scheme even in the presence of the weakest adversary.
The adversary receives two secure sketches P
1
=
{(x
1
,y
1
),. . .,(x
r
,y
r
)} and P
2
= {(x
′
1
,y
′
1
),. . ., (x
′
r
,y
′
r
)},
and its goal is to determine the coin flip, i.e., whether
the biometrics w
1
and w
2
are related or not. Let
P
x
1
and P
x
2
denote projections of P
1
and P
2
, resp.,
on the x-coordinate, i.e., P
x
1
= {x
1
,. . .,x
r
} and P
x
2
=
{x
′
1
,. . .,x
′
r
}. The basic attack idea is to compute the
intersection of P
x
1
and P
x
2
and use its size to make a
distinction between related and unrelated biometrics.
Related sketches will overlap in at least s − t orig-
inal biometric points, while unrelated sketches will
have fewer original biometric points overlap. In addi-
tion, a number of chaff points in P
x
1
can collide with
chaff points in P
x
2
or points in w
2
\ (w
1
∩ w
2
) (simi-
larly, points from w
1
\(w
1
∩w
2
) can collide with chaff
points in P
x
2
). Thus, the size of P
x
1
∩ P
x
2
follows a
certain distribution, but the expected overlap size is
larger for related sketches. We first analyze the prop-
erties of such a distribution.
Let α = |w
1
∩ w
2
| denote the number of biomet-
ric points in the intersection, i.e., α ≥ s−t for related
biometric samples and α ≤ s − t − 1 otherwise. Let
a = r−α and b = n−α, i.e., a is the number of sketch
points that do not correspond to the overlapping bio-
metric points and b is the overall space for such
points. As customary in the literature, we assume that
the biometric points of w are distributed uniformly in
the space; the chaff points are also drawn uniformly
at random from the remaining space. Then to de-
termine how many points from P
′
1
= P
x
1
\ (w
1
∩ w
2
)
will collide with points from P
′
2
= P
x
2
\(w
1
∩w
2
), sup-
pose there are b = n − α bins and points from P
′
1
oc-
cupy a = r− α of them, i.e., there are a random bins
with a ball in them. Then we throw another a balls
(points from P
′
2
) into the bins without replacement and
count the number of bins with two balls in them (i.e.,
if a bin has two balls, it is removed, so that no bin
has more than two balls; this is dictated by the re-
quirement that all r points in a sketch are distinct).
The above can be modeled as hypergeometric experi-
ment. Let X be a random variable that corresponds to
the number of collisions in P
x
1
and P
x
2
(i.e, its size is
|(P
x
1
∩ P
x
2
) \ (w
1
∩ w
2
)|). We obtain:
Pr[X = k] =
a
k
b−a
a−k
/
b
a
where X can range between 0 and a. This distribu-
tion’s mean value is E[X] = a · (a/b).
This analysis leads to the following attack strat-
egy: given sketches P
1
and P
2
, A computes P
x
1
, P
x
2
,
and c = |P
x
1
∩ P
x
2
|. Let β denote the value (r − s +
t)
2
/(n − s + t) rounded to the nearest integer. If
c ≥ (s− t + β), output 1, otherwise, output 0.
Let α
auth
(α
imp
) denote a random variable cor-
responding to the distribution of |w
1
∩ w
2
| when w
1
and w
2
are related or authentic (unrelated or impos-
tor, resp.). Adversary A has the smallest probabil-
ity of distinguishing between authentic and impostor
sketches when the values of α
auth
and α
imp
are the
closest, i.e, α
auth
= s − t and α
imp
= s − t − 1. Ac-
cording to the indistinguishability definition, we have
Adv
ind
A
= 2
Pr[b
′
= b] −
1
2
. If we let X
1
denote the
random variable distributed according to the hyper-
geometric distribution above with α
1
= s− t and X
2
denote a similar random variable with α
2
= s− t − 1,
we obtain that A is successful with at least:
Pr[b
′
= b] = Pr[b
′
= 1| b = 1]Pr[b = 1] +
+ Pr[b
′
= 0| b = 0]Pr[b = 0] ≥
≥
1
2
Pr[X
1
≥ c− α
1
] + Pr[X
2
< c− α
2
]
=
1
2
Pr[X
1
≥ β] + Pr[X
2
< β+ 1]
=
=
1
2
r−s+t
∑
i=β
r−s+t
i
n−r
r−s+t−i
n−s+t
r−s+t
+
+
β
∑
i=0
r−s+t+1
i
n−r
r−s+t+1−i
n−s+t+1
r−s+t+1
.
This probability and Adv
ind
A
can be easily computed
for a given set of parameters n, r, s, and t. In re-
ality, each parameter above has limitations placed
on it by the behavior of the actual biometric data.
In particular, (Clancy et al., 2003) study applicabil-
ity of the fuzzy vault construction to fingerprint data
and determines optimal parameters to use to achieve
adequate resistance of the construction against brute
force search (when an adversary is given a sketch and
tries to determine sensitive information by searching
through polynomials). While the fuzzy vault con-
struction was not used exactly as a secure sketch
in (Clancy et al., 2003) and was generalized, we nev-
ertheless obtain information about the parameters that
would be used for fingerprint data. The field F
p
2
,
for prime p, is used for representing fingerprint fea-
tures in 2-D and the value of p is set to 251 giving us
n = 251
2
= 63001 (this value of n also provides many
choices for the decoding algorithm). The number of
biometric points in a fingerprint was empirically de-
termined on average to be s = 38 (it can vary based on
the equipment and quality of data, but generally is in
a similar range). For this value of s, having 20 points
overlap would provide excellent distinguishing capa-
bility and low false acceptance rate (Pankanti et al.,
2002). Finally, the value of r is constrained in that the
complexity of decoding for legitimate users can grow
as r increases (this is caused by spurious polynomi-
als introduced by the chaff points). In particular, at
ON THE (NON-)REUSABILITY OF FUZZY SKETCHES AND EXTRACTORS AND SECURITY IN THE
COMPUTATIONAL SETTING
73

Figure 1: Adversary advantage Adv
ind
A
with parameters n =
251
2
, s = 38, t = 20, and varying r.
the decoding time, when a legitimate user computes
w
2
∩ S, where S = SS(w
1
), the decoding complexity
can grow when points from w
2
\ (w
2
∩ w
1
) coincide
with chaff points in S. Since |w
2
\ (w
2
∩ w
1
)| ≤ t
for legitimate users, the experiment now consists of
throwing t points in b = n − s + t bins, where a =
r − s+ t bins are already occupied. We want r to be
such that the expected (integer-valued)number of col-
lisions t(a/b) is 0.
Figure 1 plots the adversary’s advantage Adv
ind
A
for the above parameters as a function of r near the
suggested in (Clancy et al., 2003) value of r ≈ 300.
As evident from the figure, the advantage is signifi-
cant even in the worst (for the adversary) case when
only one overlapping point separates authentic data
from impostor. The jumps in the plot correspond to
the places where the (integer-valued) mean of the dis-
tribution, E[X], increases by 1.
Improved Fuzzy Vault. An important observation
in designing an attack strategy for this construction is
that it is deterministic. This immediately implies that
the same biometric will always produce the same se-
cure sketch, giving the adversary the ability to distin-
guish sketches. Thus, as an important special case we
first consider the adversary’s ability to win the indis-
tinguishability game when no noise affects multiple
sketches of the same w (this arises in several applica-
tions, where multiple keys are issued using the same
copy of w). Thus, when A obtains challenge S
2
, it
outputs 1 if S
2
= S
1
and 0 otherwise. This means that
when b = 1, A will always guess the bit correctly, but
when b = 0 it might still sometimes output 1 if the
two sketches happened to be the same. The probabil-
ity of the latter, however, is small and can be bound
as follows. Recall that sketch S consists of t coeffi-
cients of a polynomial p(x) = x
s
+ c
s−1
x
s−1
+ ... +
c
1
x + c
0
, where for w = {w
1
,. . .,w
s
} c
s−1
=
∑
i
w
i
,
c
s−2
=
∑
i6= j
w
i
w
j
, .. ., c
s−t
=
∑
C⊂[1,s],|C|=t
(
∏
i∈C
w
i
).
First, for an unrelated random biometric ˆw, the prob-
ability that
∑
i
ˆw
i
= c
s−1
is
1
n
(i.e., without any restric-
tions, there are
∏
s−1
i=0
(n − i) choices for s elements
without repetitions from the set of n elements, and
when the sum of the elements is fixed (in F
n
), the
number reduces to
∏
s−1
i=1
(n− i)).
Now consider c
s−2
. We start with a simpler func-
tion x
1
x
2
= b in F
n
for a fixed value of b. Recall
that n = p
2
for a prime p. We enumerate all pos-
sible solutions x
1
and x
2
for this function such that
x
1
6= x
2
(since all points in a biometric are different).
When b is zero, there are n−1 unordered pairs (x
1
,x
2
)
with x
1
6= x
2
whose product equals to b (one value is
zero and the other can take n − 1 remaining values).
All elements other than zero form a cyclic multiplica-
tive group, and when b 6= 0 there are either
n−1
2
or
n−1
2
− 1 pairs (x
1
,x
2
) with distinct x
1
and x
2
, when b
is a quadratic non-residue or quadratic residue, resp..
Therefore, the number of pairs (x
1
,x
2
) satisfying the
congruence for any b is at most n − 1 from the over-
all space of
n(n−1)
2
such pairs, giving us the fraction
(n− 1)/
n(n−1)
2
=
2
n
.
Now recall that c
s−2
is composed of a summa-
tion of products w
i
w
j
for each i 6= j. When there is
only one product w
1
w
2
(i.e., s = 2), we obtain that
it is equal to 0 more frequently than to other values.
When, however, s > 2 this is no longer the case. Be-
cause all w
i
have to be unique and each w
i
appears
in a number of products w
i
w
j
, the value of the sum
tends to be distributed more evenly as s increases.
This means that the frequency of the most common
value of c
s−2
approaches
1
n
when s grows. To il-
lustrate this phenomenon, we plot empirical data for
small values of n = p
2
. In particular, for s = 2, 4,
and 6 and all possible w = (w
1
,. . ., w
s
) ∈ F
s
n
we find
the value of the sum which occurs the highest num-
ber of times. Let it be denoted by count
max
and the
fraction of all biometrics w that results in such value
by f
max
= count
max
/
n
s
. To evaluate how the value
of f
max
compares to
1
n
, we plot their ratio f
max
/
1
n
in
Figure 2. For s = 2, f
max
=
2
n
is constant; for s > 2 it
is clear that f
max
rapidly approaches
1
n
from the above
even for very small values of s. This means that
2
n
is
a generous upper bound on the probability that c
s−2
of a randomly chosen ˆw will coincide with a specific
value of that coefficient for an unrelated biometric w.
Extendingthis analysis to c
s−3
=
∑
w
i
w
j
w
k
, where
i, j, and k are pairwise distinct, we obtain that the
most frequently occurring value of c
s−3
is 0 and when
s = 3 (i.e., only one product). In that case, the number
of possibilities that result in that product is
(n−1)(n−2)
2
out of
n(n−1)(n−2)
2·3
total choices (and the number of
SECRYPT 2011 - International Conference on Security and Cryptography
74
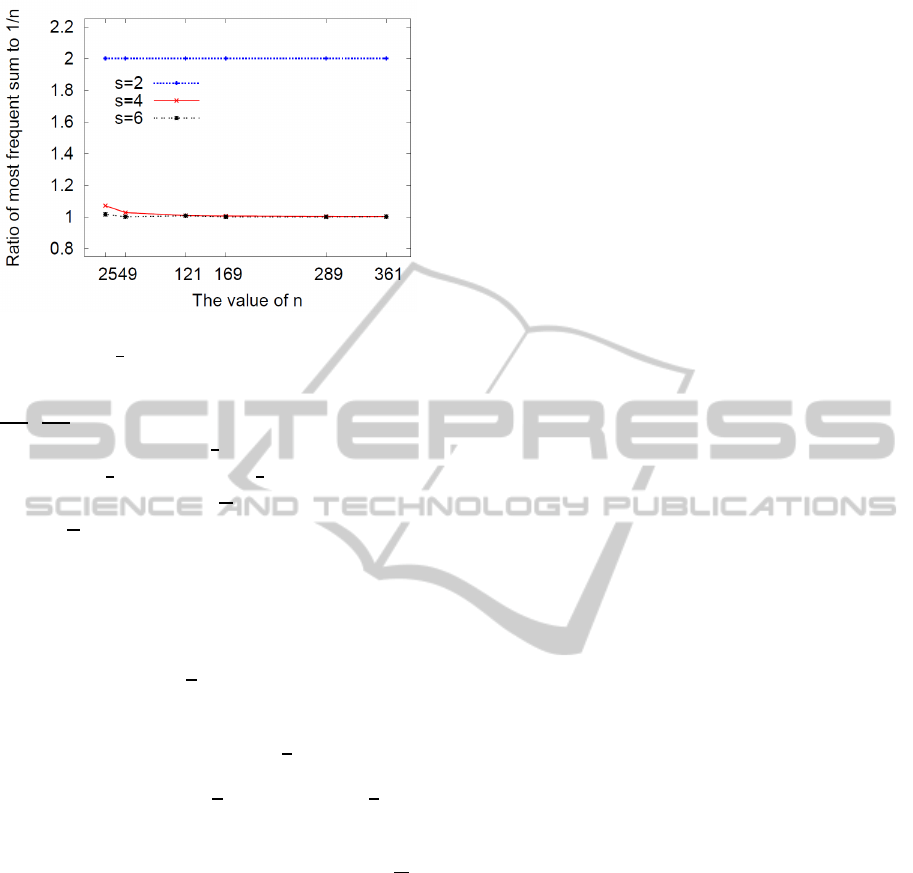
Figure 2: The ratio of the fraction of most frequent value of
the sum c
s−2
to
1
n
for varying n and s.
possibilities when the product is non-zero is at most
n−3
2
·
n−1
2
). Thus, the fraction of triples that can result
in any given product is ≤
3
n
. For c
s−4
, the maximum
fraction is ≤
4
n
; for c
s−5
, it is ≤
5
n
, etc. Therefore, the
adversarial error is at most
t!
n
t
, and in practice will be
close to
1
n
t
because s > t. Both of these quantities are
very low even for small values of t (such as 2), and the
probability with which the adversary considers two
unrelated biometrics to be related is very small. Its
advantage in the 2-indistinguishability game is:
Adv
ind
A
= 2
Pr[b
′
= b] −
1
2
=
= 2
Pr[b
′
= 1|b = 1]Pr[b = 1] +
+ Pr[b
′
= 0|b = 0]Pr[b = 0] −
1
2
=
=
2Pr[b
′
= 1|b = 1]
1
2
+ 2Pr[b
′
= 0|b = 0]
1
2
− 1
=
Pr[b
′
= 1|b = 1] + 1− Pr[b
′
= 1|b = 0] − 1
=
Pr[b
′
= 1|b = 1] − Pr[b
′
= 1|b = 0]
> 1−
t!
n
t
.
The above analysis addresses an important special
case of w = w
′
. We defer analysis of the more gen-
eral case of related sketches to the full version.
4 OUR CONSTRUCTIONS
In what follows, let (SS
′
,Rec
′
) denote any existing
fuzzy sketch scheme (for any metric). The key k de-
notes the long-term user’s key of size κ, where κ is
the security parameter. This key k is not shared with
any parties. We first provide additional definitions.
Definition 6. Let F : {0,1}
κ
× {0,1}
ℓ
1
(κ)
→
{0,1}
ℓ
1
(κ)
be a family of functions. For k ∈ {0,1}
κ
,
the function F
k
: {0,1}
ℓ
1
(κ)
→ {0,1}
ℓ
1
(κ)
is defined as
F
k
(x) = F(k,x). F is said to be a family of pseudo-
random functions (PRF) if for every PPT adversary
A with oracle access to a function F
k
and all suffi-
ciently large κ, |Pr[A
F
k
(1
κ
) − Pr[A
f
(1
κ
)]| is negligi-
ble in κ, where k
R
← {0, 1}
κ
and f is a function chosen
at random from all possible functions mapping ℓ
1
(κ)-
bit inputs to ℓ
1
(κ)-bit outputs.
Definition 7. A family of functions h : {0,1}
κ
×
{0,1}
n
→ {0,1}
ℓ
2
(κ)
is pairwise independent univer-
sal hash function if for all x, x
′
∈ {0,1}
n
, where x 6= x,
Pr[h
y
(x) = h
y
(x
′
)] = 1/2
ℓ
2
(κ)
for y ∈ {0,1}
κ
.
In the following secure sketch construction, it is re-
quired that ℓ
1
(κ) ≥ |SS
′
(w)|, where |a| is the length
of string a. We discuss the choice of parameters later.
To compute SS(w,k):
1. Choose r
1
∈ {0,1}
ℓ
1
(κ)
at random.
2. Output S = (S
1
,S
2
) = (r
1
,F
k
(r
1
) ⊕ SS
′
(w)).
To compute Rec(w
′
,k,S = (S
1
,S
2
)):
1. Compute u ← F
k
(S
1
).
2. Output what Rec
′
(w
′
,S
2
⊕ u) outputs.
Theorem 1. Assuming that F is a family of PRFs, the
above fuzzy sketch scheme achieves weak biometric
privacy.
We omit security proofs due to space constraints.
Note that in our construction deterministic
schemes for the underlying SS
′
are preferred because
they produce most concise sketches. So far we as-
sumed that the output length of F, ℓ
1
(κ), is at least as
large as the output length of secure sketch |SS
′
(w)|.
While this will hold for many types of biometrics and
a reasonable choice of security parameter κ, in some
cases the representation of SS
′
(w) can be longer. In-
stead of increasing κ, we suggest modifying the al-
gorithm to use more than one application of F to
produce a longer pseudo-random sequence. For in-
stance, if ℓ
1
(κ) < |SS
′
(w)| ≤ 2ℓ
1
(κ), the sketch can
be produced as (r
1
,(F
k
(r
1
)||F
k
((r
1
+ 1) mod 2
κ
)) ⊕
SS
′
(w)), where || denotes string concatenation. This
increases the number of random values on which F is
evaluated and thus the probability of their collision.
However, as long as |SS
′
(w)|/ℓ
1
(κ) is a constant or
polynomial in κ, the security guarantees still hold.
In the fuzzy extractor construction below we split
the key k into two keys k
1
and k
2
. This is done to
simplify the analysis. In practice, the sub-keys k
1
and
k
2
can be computed by applying a PRF keyed with k
to two different inputs.
To compute Gen(w,k
1
,k
2
):
1. Compute S = SS(w,k
1
) using the fuzzy sketch
scheme above.
ON THE (NON-)REUSABILITY OF FUZZY SKETCHES AND EXTRACTORS AND SECURITY IN THE
COMPUTATIONAL SETTING
75

2. Choose r
2
R
← {0,1}
κ
and compute s ← h
r
2
(w).
3. Output P = (S,r
2
) and R ← F
k
2
(s).
To compute Rep(w
′
,k
1
,k
2
,P = (P
1
,P
2
))
1. Run Rec(w
′
,k
2
,P
1
) above to recover w. If it fails,
output ⊥.
2. Otherwise, reproduce the key R as F
k
2
(s
′
), where
s
′
← h
P
2
(w), and output R.
When it is desirable that failures during reconstruc-
tion are not reported explicitly, Rep can be modified
to output a (wrong) private string, e.g., computed as
R = F
k
2
(h
P
2
(w
′
)).
We would like to explain the design choices made
in our construction. Because a PRF is a powerful
primitive, it by itself is sufficient to produce the pri-
vate string R indistinguishable from random. For ex-
ample, setting R ← F
k
2
(w||r) for random r would sat-
isfy the security game requirements. The reason for
including the hash function h in the construction is to
compress the biometric w without loosing the amount
of its unpredictability. That is, the n-bit representation
of biometric is normally substantially longer than the
m bits of entropy it contains. For example, for iris the
standard values of these parameters are n = 2048 and
m = 256. Because m ∼ κ, we can use a hash function
h : {0,1}
κ
× {0,1}
n
→ {0, 1}
m
to reduce the size of w
from n to m bits without loosing its entropy. In cases
when the value of m exceeds the desired length of the
input to a PRF, the hash function output length can be
further reduced, i.e., in general ℓ
2
(κ) ≤ m.
We note that the generic conversion of a secure
sketch to a fuzzy extractor (in Section 2.1) uses a
strong extractor, which can be built using a univer-
sal hash function alone. The use of the hash function
in a strong extractor is, however, constrained in that
the output length of the extractor must necessarily be
smaller than m to be able to meet the requirement of
the output being close to the uniform distribution. In
particular, at least 2log(
1
ε
)− 2 bits of entropy are lost,
where the parameter ε determines the statistical dis-
tance between distribution of the output and the uni-
form distribution. In our case, no requirements on the
uniformity of the output must be met, and therefore
no reduction of the output length or entropy loss has
to take place.
Theorem 2. Assuming that F is a family of PRFs
and h is a universal hash function, the above fuzzy
extractor scheme achieves strong biometric privacy.
We would like to note that certain constructions of
PRFs are known to produce uniformly distributed se-
quences. For example, (Shparlinski, 2001) shows that
PRF in (Naor and Reingold, 1997) has this property
for almost all values of parameters. For us this means
that the adversary does not obtain advantage in distin-
guishing pseudo-random strings from random.
We also note that similar results can be achieved
by using encryption instead of PRF, and such schemes
might be known or used in industry.
5 RELATED WORK
The overall literature on fuzzy sketches and extrac-
tors is extensive, and we therefore highlight the most
fundamental results and analysis related to this work.
(Davida et al., 1998) proposed the first off-line bio-
metric identification scheme, where error-correcting
codes were used to reconstruct a biometric from its
noisy readings. (Juels and Wattenberg, 1999) devel-
oped a fuzzy commitment scheme, which became the
basis of the code-offset secure sketch for the Ham-
ming distance. (Juels and Sudan, 2002) proposed a
fuzzy vault scheme. (Dodis et al., 2004; Dodis et al.,
2008) formalized the notion of secure sketches and
fuzzy extractors in their seminal work, which gave a
generic conversion from a secure sketch to a fuzzy
extractor and developed a number of other schemes.
(Boyen et al., 2005) introduced robust fuzzy ex-
tractors secure against active adversaries, where the
reconstruction process fails if the sketch has been
tampered with. (Dodis et al., 2006) continue that line
of research and also study the keyed setting in the
bounded storage model. The use of the key in our set-
ting is fundamentally different from that work, where
two parties share a long-term secret key and use it to
generate a session key for data authentication. Our
constructions can potentially be applied to a robust
fuzzy extractor to improve reusability properties.
There are also publications that combine fuzzy
extractors with passwords to improve their security
properties such as (Ballard et al., 2008). This work
offers a simpler and more flexible construction.
Security requirements for adequate use of fuzzy
sketches and extractors in cryptographic applications
have been developing over time. (Boyen, 2004)
showed that a number of original constructions can-
not be safely applied multiple times to the same bio-
metric. That work developed improved constructions
using certain error-correcting codes and permutation
groups that satisfy the reusability requirements. Our
security definitions for the strong adversary were in-
fluenced by that work. Compared to (Boyen, 2004),
our solution leaks no information about the biomet-
ric data (while leakage is unavoidable in the setting
of (Boyen, 2004)) and works for all distance metrics
and all secure sketch schemes in the standard model
(while Boyen’s scheme is limited to special codes and
SECRYPT 2011 - International Conference on Security and Cryptography
76

a particular metric in the random oracle model).
(Scheirer and Boult, 2007) proposed three classes
of attacks on secure sketches and fuzzy vault in partic-
ular, one of which is equivalent to sketch reusability.
It has been empirically evaluated in (Kholmatov and
Yanikoglu, 2008) on the fuzzy vault scheme using 200
matching pairs of fuzzy vault sketches. The authors
were able to unlock (i.e., reconstruct the polynomial)
118 out of 200 pairs within a short period of time. We
note that this evaluation was performed on a specific
set of parameters already knowing that two stored
sketches are related. Our analysis, on the other hand,
is more general and can be applied to a wide variety
of parameters. It is also does not assume prior knowl-
edge of related sketches, but rather helps to identify
those records. (Poon and Miri, 2009) also describe
collusion attacks on the fuzzy vault scheme assuming
that the sketches are related. Finally, (Simoens et al.,
2009) introduced the notions of indistinguishability
and irreversibility for reusable sketches and showed
weaknesses of code-offset and permutation groups
constructions. We analyze other constructions with
respect to the indistinguishability property. (Kelk-
boom, 2010) also analyzes certain schemes.
6 CONCLUSIONS
This work investigates the reusability properties
of secure sketch and fuzzy extractor constructions.
Through new analysis we show that, in addition to
the schemes that have been previously shown to have
security weaknesses, other existing schemes do not
meet our security expectations. To mitigate the prob-
lem, we propose to use the computational setting.
Maintenance of a single key for all uses of such
schemes results in solutions with remarkable secu-
rity and usability improvements which are not possi-
ble otherwise. In particular, our general construction
works with any existing secure sketch and mitigates
information leakage associated with biometrics in the
standard model under generic hardness assumptions.
REFERENCES
Ballard, L., Kamara, S., Monrose, F., and Reiter, M. (2008).
Towards practical biometric key generation with ran-
domized biometric templates. In ACM CCS.
Blanton, M. and Hudelson, W. (2009). Biometric-based
non-transferable anonymous credentials. In ICICS,
pages 165–180.
Boyen, X. (2004). Reusable cryptographic fuzzy extractors.
In ACM CCS, pages 82–91.
Boyen, X., Dodis, Y., Katz, J., Ostrovsky, R., and Smith, A.
(2005). Secure remote authentication using biometric
data. In EUROCRYPT, pages 147–163.
Clancy, T., Kiyavash, N., and Lin, D. (2003). Secure
smartcard-based fingerprint authentication. In ACM
SIGMM Workshop on Biometrics Methods and Appli-
cations, pages 45–52.
Davida, G., Frankel, Y., and Matt, B. (1998). On enabling
secure applications through off-line biometric identi-
fication. In IEEE Symposium on Security and Privacy,
pages 148–157.
Dodis, Y., Katz, J., Reyzin, L., and Smith, A. (2006). Ro-
bust fuzzy extractors and authenticated key agreement
from close secrets. In CRYPTO, pages 232–250.
Dodis, Y., Ostrovsky, R., Reyzin, L., and Smith, A. (2008).
Fuzzy extractors: How to generate strong keys from
biometrics and other noisy data. SIAM Journal of
Computing, 38(1):97–139.
Dodis, Y., Reyzin, L., and Smith, A. (2004). Fuzzy extrac-
tors: How to generate strong keys from biometrics and
other noisy data. In EUROCRYPT, pages 523–540.
Dodis, Y. and Smith, A. (2005). Correcting errors with-
out leaking partial information. In ACM STOC, pages
654–663.
Juels, A. and Sudan, M. (2002). A fuzzy vault scheme. In
International Symposium on Information Theory.
Juels, A. and Wattenberg, M. (1999). A fuzzy commitment
scheme. In ACM CCS, pages 28–36.
Kelkboom, E. (2010). On the performance of helper data
template protection schemes. PhD thesis, University
of Twente.
Kholmatov, A. and Yanikoglu, B. (2008). Realization of
correlation attack against the fuzzy vault scheme. In
Proceedings of SPIE, volume 6819.
Naor, M. and Reingold, O. (1997). Number-theoretic con-
structions of efficient pseudo-random functions. In
IEEE FOCS, pages 458–467.
Nisan, N. and Ta-Shma, A. (1999). Extracting randomness:
A survey and new constructions. Journal of Computer
and System Sciences, 58:148–173.
Pankanti, S., Prabhakar, S., and Jain, A. (2002). On the in-
dividuality of fingerprints. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 24(8):1010–
1025.
Poon, H. and Miri, A. (2009). A collusion attack on the
fuzzy vault scheme. ISC International Journal of In-
formation Security, 1(1):27–34.
Scheirer, W. and Boult, T. (2007). Cracking fuzzy vaults
and biometric encryption. In IEEE Biometrics Sym-
posium, pages 1–6.
Shparlinski, I. (2001). On the uniformity of distribution
of the Naor-Reingold pseudo-random function. Finite
Fields and Their Applications, 7(2):318–326.
Simoens, K., Tuyls, P., and Preneel, B. (2009). Privacy
weaknesses of biometric sketches. In IEEE Sympo-
sium on Security and Privacy, pages 188–203.
Smith, A. (2004). Maintaining secrecy when information
leakage is unavoidable. PhD dissertation, MIT.
ON THE (NON-)REUSABILITY OF FUZZY SKETCHES AND EXTRACTORS AND SECURITY IN THE
COMPUTATIONAL SETTING
77
