
RESEARCH ON THE INFORMATION GLOBULAR RADIATION
MODEL IN CYBERSPACE
Niannian Jia, Jiannan Yu and Yunfan Xia
School of Science, Harbin Engineering University, Harbin, China
Keywords: Cyberspace, Information diffusion, Globular radiation, Measure distribution of information.
Abstract: According to advantage of information diffusion in cyberspace, the process of information diffusion can be
simulated a compound process of time-variation and space spreading. On basis of Network Dimension-force
theory, this paper builds the information globular radiation model in cyberspace. Starting with the ideal
cyberspace and reality cyberspace, the model simulates the process of information diffusion with time as the
diffuse radius and the amount of information as the diffuse volume. Using physics properties and rigorous
mathematical reasoning, the paper proved existence and rationality of the model, which provided new
directions for network information diffusion.
1 INTRODUCTION
With the rapid development of network, the world
enters into the information age charactered by high
efficiency. Owing to network, the superiorities of
information diffusion is mainly about small time
difference but large quantity. From the point of view
of information science, information diffusion in
cyberspace is a process of information diffusing
from one node to the whole space .In other words, it
is a compound process of time-variation and space
spreading (Zhao, 2006). From the perspective of the
cyberspace, complicated network is abstracted into
nodes and paths (Deng, 2008). The nodes represent
the location of the information, and the paths
represent the area of flow of information. The paper
advances a completely new model of information
diffusion in cyberspace on the basis of the above-
mentioned two views, namely globular radiation
model of information in cyberspace.
2 THE THEORETICAL
RESEARCH ON THE
GLOBULAR RADIATION
MODEL OF INFORMATION
IN CYBERSPACE
2.1 The Definition of Cyberspace
The three elements of cyberspace are information,
information nodes and paths between nodes.
Therefore cyberspace is defined as three-
dimensional vector
1
{,,}
M
PL .
12
,,,
n
M
mm m
represents a set of flowing information in
cyberspace, where
i
m flowing in connecting paths
and existing on the network nodes is a set of
information. Considering information with
properties of sets, therefore
i
mM . Otherwise
i
m
is called fake information of
M
(Chen, 2004).
12
{, , , }
n
Ppp p represents a set of nodes in
cyberspace. In the theory of Network Dimension-
force, information source nodes are divided into two
types: shining point and vanishing point. A shining
point represents the node being able to send out
information, while a vanishing point represents the
opposite. Information sink nodes can be classified as
reachable points and unreachable points. A
reachable point is the node being able to receive
information, while an unreachable point is the
418
Jia N., Yu J. and Xia Y..
RESEARCH ON THE INFORMATION GLOBULAR RADIATION MODEL IN CYBERSPACE.
DOI: 10.5220/0003569804180422
In Proceedings of the 13th International Conference on Enterprise Information Systems (NMI-2011), pages 418-422
ISBN: 978-989-8425-53-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
opposite.
11
{, ,, , }
ij nn
L
lll represents the set of
paths of network space.
ij
l
represents the path
between
i
p and
j
p .When
i
p and
j
p are both
shining points or reachable points,
ij
l is called access
.When at least one of
i
p and
j
p
is vanishing point
or unreachable point,
ij
l is considered as a broken
path or inexistent.
2.2 The Mode of Information Diffusion
in Ideal Cyberspace
In cyberspace, the information diffusion is a process
of information transmitted from one point to another
(Deng, 2008). In ideal cyberspace, the information
dissemination is not affected by any restraints of
objective and subjective conditions .In such a
circumstance all the information source nodes are
shining points, and all the information sink nodes are
reachable points .All the paths
ij
l
are connected.
Therefore, in ideal cyberspace the information on
the information source node is transmitted to the
numerous information sink nodes in diffuse way
during
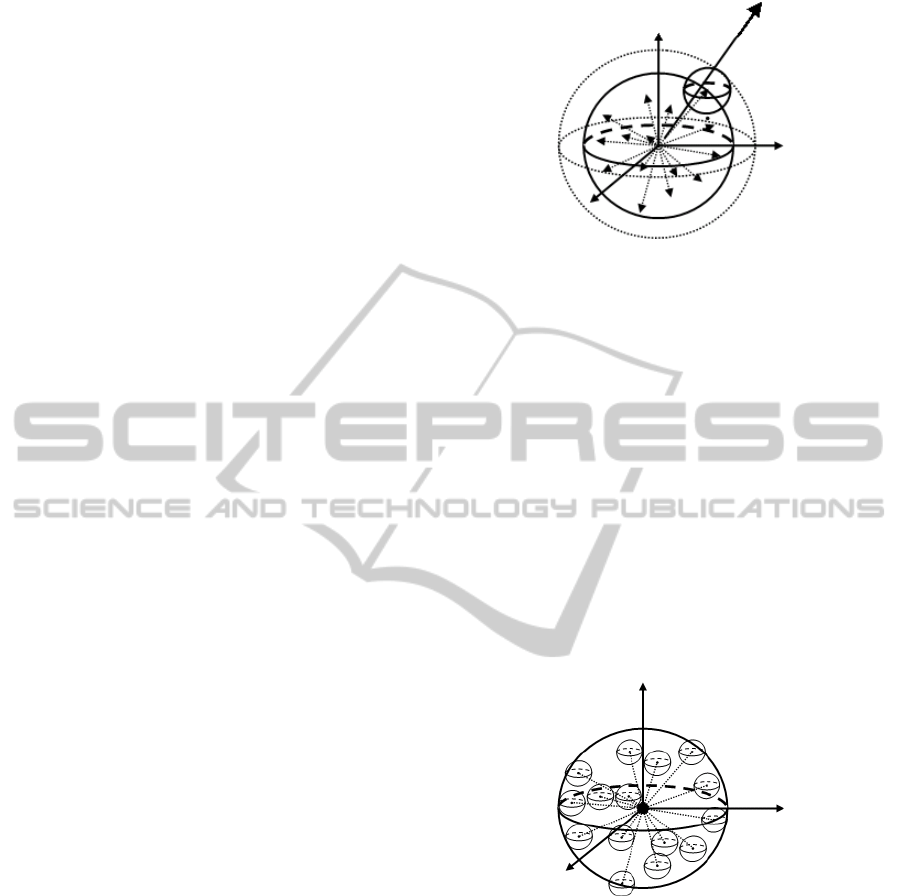
(0)tt . As Fig. 1 showed, the numerous
nodes formed a spherical surface with
t as the
radius. The surface is formed by the information
transmitted to all the information sink nodes after
t . During the next t , all the information sink
nodes become information source nodes, then the
information on the nodes is transmitted to the
numerous new information sink nodes in diffuse
way. Obviously, a new spherical surface is formed
by each node. Because
0t
, a new spherical
surface is formed out of the previous one with the
same sphere’s center, but the radius of the new
spherical surface is 2
t . So when the number of t
approaches infinite, numerous spherical surfaces,
with
(1,2,...)ntn as their individual radius
and the same center, are formed. Thus, a sphere with
tnt as the radius is formed after nt
.The
formation of the sphere with
t is the process of the
information diffusion in the ideal cyberspace. This
diffusion way is there-dimensional from point to
plane. The information transmission mode is
constructed as globular radiation model of
information in ideal cyberspace (Cai, 2010). The
model can fully reflect that information diffusion is
a complex process of time variation and space
spreading. This section must be in one column.
Figure 1: The picture of the process of the information
diffusion.
2.3 The Mode of Information Diffusion
in Reality Cyberspace
Unlike in the ideal cyberspace, however,
information can not spread to every information
node in the reality cyberspace .Due to various
reasons, a few information nodes related to the
information of information source are not able to
receive information .Such information node is called
vanishing point of information. According to
different kinds of information, the number of the
vanishing points of information is different. A
vanishing point can lead to a number of unreachable
points. Figure 2 is a schematic illustration of
vanishing point of information.
Figure 2: The picture of vanishing points of information
diffusion.
2.4 The Globular Radiation Model of
Information in Cyberspace
Described as the globular radiation model of
information in ideal cyberspace, it is the amount of
information of diffusing that formed infinitely many
spherical surfaces with
(1,2,,)ntn
as their
radius and the same center. The amount of
information of diffusing formed a sphere with
tnt
as the radius. Let
2
() 4 ( )
s
tt
, where
()
s
t is the surface area of the sphere at time t and
RESEARCH ON THE INFORMATION GLOBULAR RADIATION MODEL IN CYBERSPACE
419

is time-intensity parameter. Because ()
s
t is an
integrable function on interval
[0, )
,
()qt = ()Vt =
2
0
4()
t
rtdt
=
3
4
()
3
t
()t . ()qt , the total number of information at
time
t in an ideal state, accord with the variation
rule of the volume of the sphere with
t
as the
radius.
In the reality cyberspace, under the influence of
various subjective and objective conditions,
information nodes that can not transmit information
with time are existent. In other words,
12
{, , , }
n
Ppp p ,the set of nodes, has vanishing
point or unreachable point
i
p . As figure 2 shows,
more new vanishing points and unreachable points
are caused by these vanishing points and
unreachable points. Information transmission would
produce the losses of the amount of information with
an obvious randomness in the reality cyberspace,
namely
3
4
() () ( )
3
RI
qt qt t
, where
()
I
qt
represents the total information of the ideal
cyberspace and
()
R
qt represents the total
information of the reality cyberspace.
3 THE PROOF OF GLOBULAR
RADIATION MODEL OF
INFORMATION IN
CYBERSPACE
When describing the cyberspace, there is an
important measure, network measure distribution
function
()k
, the definition of which is the
probability of the node randomly selected with
k
connecting paths. In the globular radiation model
of information in cyberspace, the shorter the
connecting time
t among points, the more the
paths
k from point to point. Therefore there are a
certain inverse relationship between time t and
connecting path
k , namely
1
k
t
.According to the
study in recent years, the network measure
distribution function shows power exponent law,
namely
()kk
, so
()kt
, where
is
power exponent
(Wang, 2004). The basic
constitution of the globular radiation model of
information in cyberspace is as follows. Starting
with
0t , there are at least
(0)( (0) 1)
information originating nodes. ()t
represents the number of nodes in cyberspace at time
t . After that the following four processes would
happen during every
t
time step.
1) Some information source nodes are vanishing
points in cyberspace, and information source nodes
becoming vanishing points are stochastic. Let the
number of the nodes without information sent out
is c .
2) Stochastic selection of diffusion, information
sink nodes receive information transmitted by
information source in the reality cyberspace on the
basis of competitive selection .The number of
information sink nodes is several ,therefore
information source nodes and information sink
nodes would produce
e connecting paths
ij
l between
nodes .The preferential probability that information
source node
0
p reaches information sink node
i
p ,
i
i
j
j
k
k
(1)
3)
r connecting paths of information nodes in
cyberspace as
ij
l :a connecting path is the path from
shining points to reachable points, the preferential
probability of the information source node
determined by (1).
4)
n broken paths of information nodes in
cyberspace as
ij
l : when information sink nodes are
unreachable points, information sent to space can
not be received ,which would cause broken paths.
Meanwhile information source node
0
p are selected
in anti-preferential probability (Jia, 2009)
'
1
() 1
i
i
t
(2)
Consequently,
() (1 )tcte
. ()t
represents the
total measure of the nodes in cyberspace at time
t
,namely
()
j
j
tk
.Therefore
()
()
()
t
kt
t
at
time
t ,where ()kt represents the average measure of
information nodes at time
t .
According to Dynamical Mean-Field Theory,
(Xu, 2010)measure distribution of node
i
p in
cyberspace can be obtained. If
i
k is successive,
i
k
satisfies
(1 )
()
ii
iiij
ij
kk
er r
tt
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
420

''
(1 )
iij
ij
n
(3)
And average measure distribution of information
nodes in
t
time is
2[ ( ) ]
()
()
()
1
eckt rn
t
kt
t
c
(4)
Then
2( )
()
1
ern
kt
c
when
t .Insert
function
() (1 )tct
and
average measure
distribution of information nodes into
(4),where
2( )(1 )
()
1
ern c
tt
c
(5)
Applying (3) with
()t
、 ()t
, we obtain
approximating linear differential equation
22 21
2( )(1 ) 1
ii
kk
ercecn n
ternct ct
(6)
Let
22
2( )(1 )
e r ce cn
x
ern c
,
2
1
n
y
c
, initial
condition is
()
i
kt e ,whence
() ( )( )
x
ii
i
yt y
kt e
x
tx
(7)
The solution of the inequality
()
ii
kt k
is
1
x
i
y
e
x
tt
y
k
x
(8)
Therefore
1
()( )
x
ii
y
e
x
kk tt
y
k
x
1
1( )
x
i
y
e
x
tt
y
k
x
(9)
If
i
t satisfying homogeneous distribution (Samuel,
2009), measure distribution function of information
nodes is
1
1
()
()
1
()
(0)
()
x
i
x
x
y
e
kk
t
x
k
kxt
y
k
x
(10)
So when time is
(1,2,...,)tntn , then
1
1
() ( )( )
x
y
y
ke k
x
xx
(11)
While
12( )(1)
11
()(1)2
ern c
x
er c cn
(12)
We have on the basis of (11) that information nodes
measure distribution function
()k
have parameter
exponent and power exponent, and power exponent
is to correspond with
1
1
x
. Since
1
k
t
and (1,2,...,)tntn
, therefore
()kt
,thus, ()qt t
. In the information
globular radiation model in network, time
t
be a
continuous increasing variable, clearly the
parameters show that
0, 0 1, 0, 0,ecrnern
. Inserting this
parameters into (12), the power exponent
is to
correspond with
13
. Firstly, while 1
, it
indicates the information is being transmitted and
received from the source nodes. While
01
,
there is no source node or the source point transmit
nothing in the cyberspace. While
13
, there are
vanishing and unreachable points in the cyberspace.
Only when
3
, the cyberspace is ideal, where all
the source nodes are shining points and all the sink
nodes are reachable points. Therefore the quantity of
information function can be illustrated as
3
4
() ( )
3
qt t
(0 )t
. This equation meets
suppose of information diffusion spherical radiated
model in ideal cyberspace.
4 CONCLUSIONS
Network Dimension-force discovered that network
provided the superiority in time and space to
information diffusion. This paper based on this
superiority build the information globular radiation
model in network space, to show the process of
information diffusion is the complex process of
network information with time variation and space
spreading. And the model of existence and
rationality has proved though the physics nature of
network, for this reason, the information globular
radiation model in network space is able to describe
information diffusion in cyberspace. Thereby this
model is suitable in research on information
diffusion in cyberspace and analysis of the problems
of network information.
RESEARCH ON THE INFORMATION GLOBULAR RADIATION MODEL IN CYBERSPACE
421

ACKNOWLEDGEMENTS
This work supported by The Fundamental Research
Funds for the Central Universities (Grant
HEUCF20111135).
REFERENCES
Zhao J. L., 2006. Network Dimension-force Based on
Original Philosophy and Management Innovations.
Harbin: Harbin Engineering University Doctor Paper.
Deng Y. R., 2008. Research on Information Diffusion
Based on Network Dimension-force.
Harbin: Harbin
Engineering University Doctor Paper.
Chen J., 2004.
The Research on Free Degree of Network
Information Transmission Based on Internet.
Wuhan:
HuaZhong Normal University.
Deng Y. R., 2008. Research on the Dynamic Mechanism
of Information Diffusion in Network Environment.
Library and Information Service.
Cai C., 2010. Research of Models and Integration for 3D
Spatial Data.
Geospatial Information.
Wang W. N., 2004. On the Topology of Complex
Networks in the Information Networks. Nanjing:
Journal of Nanjing Institute of Posts and
Telecommunications (Natural Science).
Jia X. L., 2009.A Dynamic Scale-free Network Model.
Sichuan:
Journal of Sichuan Normal University
(Natural Science).
Xu S. H., 2010. Analysis of Knowledge Transfer Network
Characteristics Based on Small-world Network Model.
Journal of the China Society for Scientific and
Technical Information.
Samuel Karlin, 2009. Howard M. Taylor.
A Second
Course in Stochastic Processes
. Beijing Posts &
Telecom Press.
ICEIS 2011 - 13th International Conference on Enterprise Information Systems
422
