A NEW METHOTOLOGY FOR ADAPTIVE FUZZY

CONTROLLER. COMPARISON PERFORMANCE AGAINST

SEVERAL CONTROL ALGORITHMS IN A REAL TIME

CONTROL PROCESS

Rafik Lasri, Ignacio Rojas, Héctor Pomares and Fernando Rojas

Dep. Computer Architecture & Computer Technology, E.T.S. Ing. Informática & Telecomunicación

Univ. of Granada, Periodista Daniel Saucedo Aranda, s/n, E-18071, Granada, Spain

Keywords: Adaptive Fuzzy Controller, Temperature Control, Real-time Control, PID Control Process.

Abstract: This article presents a comparative study of various control algorithms. An adaptive fuzzy logic controller is

set to prove its effectiveness against other conventional controllers in a simulated control process as well as

in a real environment. Through a training board that allows us to control the temperature, we can compare

the behavior of each used algorithm. The adaptive fuzzy logic controller will be required to present a real

high performance in temperature control, having in mind that the adaptive algorithm starts with no rules set

i.e., empty rule base or by assigning arbitrary values to the rules without any information off-line. The

comparison of results clearly shows the great contribution that the policy of an adaptive algorithm brings;

ease of implementation and high accuracy.

1 INTRODUCTION

An intelligent control system typically consists of

two parts: the firstis the “knowledge base” which

presents the necessary knowledge to control the

plant, and the second is an “inference engine” which

processes the knowledge through reasoning,

possibly using a new set of data to obtain the

decision. Our study uses intelligent control

techniques based on fuzzy logic and PID controller

structures. Several structures of controllers have

been tested in this control process to demonstrate the

profitability of our adaptive fuzzy controller.

During the past 30 years numerous studies have

presented several examples of adaptive controllers.

In the 70sE.H. Mamdani and his student S. Assilian

(Mamdani and Assilian, 1975) to determine the

responsible rule for the undesirable state of the plant

and replace it with the appropriate value, these steps

have initialized a new policy of adaptive fuzzy logic

controllers it calling Self Organizing Control (SOC)

system (Procyk, 1979). In most SOC approaches,

this dependence is expressed using only the

monotonicity sign of the plant (Cho, 2002; Fan,

2004; Hua, 2004; K.Lin, 2003; M.Lin, 2004; Park,

2005; Velagic, 2003; Velez-Diaz, 2004; Yi, 2002).

The main focus of this paper is to prove that our

adaptive fuzzy controller is capable of achieving a

high accuracy and a good robustness through

modifying the consequents of the rules in real time,

the controller determines in which sense the rules

have to be moved i.e., auto-learning. The proposed

methodology is robust against modification of the

parameters of the plant (break-downs). It is

important to note, that no initial knowledge about

the control policy is required and therefore the fuzzy

controller can start with a set of empty rules.

2 TEMPERATURE CONTROL:

THE HARDWARE

DESCRIPTION

In this paper we will try to simulate the control of

temperature of a room using a training board with

several intelligent control algorithms. Our goal is to

maintain the temperature of the room at a desired

value; the room is equipped with a temperature

source that heats the environment and a fan for

470

Lasri R., Rojas I., Pomares H. and Rojas F..

A NEW METHOTOLOGY FOR ADAPTIVE FUZZY CONTROLLER. COMPARISON PERFORMANCE AGAINST SEVERAL CONTROL ALGORITHMS

IN A REAL TIME CONTROL PROCESS.

DOI: 10.5220/0003647204700474

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 470-474

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

lowering the temperature in cases of over passing

the set point. The controller will aim to generate the

fan power signal and determining their performance

rating regard to the difference between the sensed

temperature inside the room and the required

temperature.

3 DESIGN AND

IMPLEMENTATION OF THE

USED CONTROLLERS

3.1 Tuning the PID Controllers

The Ziegler–Nichols closed loop (Ziegler, 1942),

tuning method is a heuristic method of tuning a PID

controller. It is performed by setting the I (integral)

and D (derivative) gains to zero. The P

(proportional) gain is then increased (from zero)

until it reaches the ultimate gain K

, at which the

output of the control loop oscillates with a constant

amplitude. K

and the oscillation period P

are used

to set the P, I, and D gains depending on the type of

controller used.

Figure 1: Ideal tuning phase of the Ziegler-Nichols closed

loop method.

Table 1: Formulas for the controller parameters in the

Ziegler-Nichols closed loop method.

Structures Parameters

Kp Ti Td

P controller

PI controller

PID controller

0.5 Kp

∞ 0

0.45Kp

/ 1.2 0

0.6 Kp

/ 2 P

/ 8

3.2 Design of a Static Fuzzy Logic

Controller

Due to its simplicity and stability we chose a TSK-0

fuzzy logic controller (static controller), with two

inputs and one output. The controller inputs are the

temperature error and its derivative (Te, Tė), the

error is the difference between the required

temperature Tsp and the temperature at instant i (Ti),

in fact the error equation is: Te = Tsp – Ti. The

controller output is the tension that controls the fan

operation. The inputs have a set of membership

functions describing the state of these variables in

their natural space, limited by its real extreme limits.

The first input has seven and the second one has fife

triangular membership functions covering the whole

range of variation. The output is a set of scalar

values (TSK-0 type controller).

3.3 Implementation of an Advanced

(Adaptive) Fuzzy Logic Controller

in Real Time

In this article, we used the product as T-norm for the

fuzzy inference method and the ‘‘centre of gravity’’

with sum-product operator as the defuzzification

strategy. Using the above notation, we can express the

output of the fuzzy controller as follows:

⎛⎞

⋅

⎜⎟

⎝⎠

⎛⎞

⎜⎟

⎝⎠

∑∑ ∑ ∏



12 N

i i ...i v

i=1i=1 i =1 v=1

(x )

F(x ) =

μ (x )

(1)

where

is the N-dimensional input vector at

instant k. The adaptive algorithm used, will be able

to adapt the controller parameters using the

information obtained from the current error in the

output of the plant. The correction sense is deduced

from the monotony of the plant.

In the algorithm subject of this study, coarse

adaptation of the fuzzy rule consequents is achieved

by evaluating the current state of the plant and

proposing a correction of the rules responsible for

the existence of such a state, either as a reward or as

a penalty, in the following way:

(2)

where:

µi

...i

is the strength or α-level of rule

...i

, and e

(k) is the error at instant k.

Figure 2: Adaptive fuzzy controller.

Since, as in (Rojas, 1999), the degree with which the

rule was activated in achieving the control output

u(k-d) was used proportionally with the modification

()

)()()·(·

)()·(·)(

...

......

2121

kydkrdkC

kedkCkR

iii

yiiiiii

−−−

=−=Δ

A NEW METHOTOLOGY FOR ADAPTIVE FUZZY CONTROLLER. COMPARISON PERFORMANCE AGAINST

SEVERAL CONTROL ALGORITHMS IN A REAL TIME CONTROL PROCESS

471

adopted now being evaluated at instant k. In the

aforementioned expression, d represents the time

delay, r(k-d) is the required set point of the plant

output at instant k-d and y(k) is the current plant

output, it is very important to clear up that using r(k)

would be incorrect, because the rules that are

activated at instant k-d serve to achieve the desired

value r(k-d) and not r(k). The determination of the

absolute value of the coefficient C is calculated

spent in off-line using the formula: |C| = ∆u/∆y,

where ∆y is the operation range of the plant output ,

which must be estimated beforehand from the

knowledge about the set points that we are going to

use, and ∆u is the operation range of the controller’s

actuator. In our case and after studying our plant we

chose |C|= 15.

4 SIMULATION RESULTS

4.1 Real Simulation: Temperature

Control

The MSE calculated in this study is not the MSE of

the function approximation by the controller but it‘s

the MSE between the set point and the plant output

measured after d instants of time, being d the delay

of the plant.

MSE = 

∑

(

(



)

())









_

(3)

4.1.1 Temperature Control Using a P, I and

D Control Policy

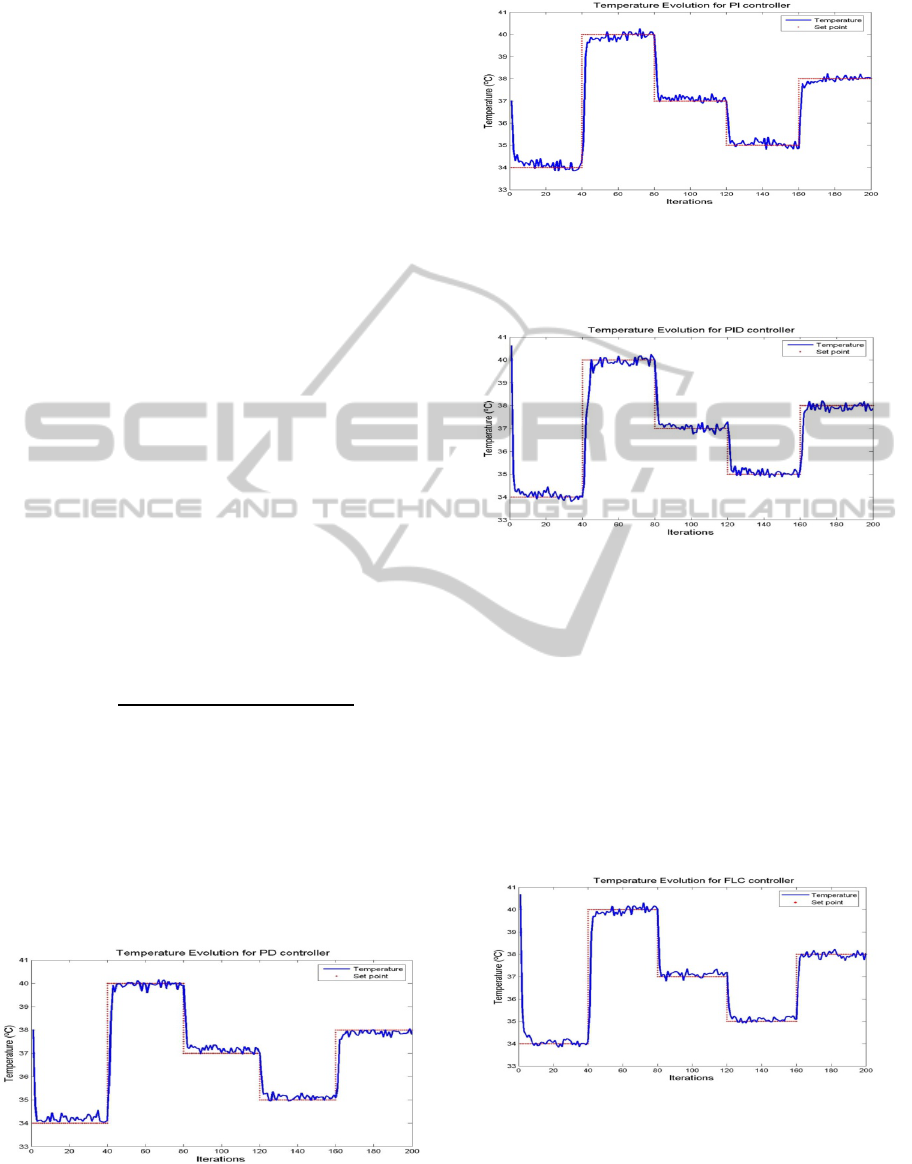
• The PD and PI Controllers

The PD and PI controllers have been able to control

the temperature, the MSE (mean squared error) for

the last 40 iterations are respectively around 0.49

(Fig. 3) and 0.43 (Fig. 4).

Figure 3: Control evolution with PD algorithm for various

set points.

Figure 4: Control evolution with PI algorithm for various

set points.

• Using a Full PID Controller

Figure 5: Control evolution with PID algorithm for various

set points.

Fig. 5 clearly shows that our PID works well as a

controller for various values of set points,

guaranteeing the convergence around the set point

with a 0.47 MSE in the last 40 iterations.

4.1.2 Temperature Control using a Static

Fuzzy Logic Controller

Fig. 6 shows that the static fuzzy logic controller is

performing well. The MSE for the last 40 iterations

is 0.31.

Figure 6: Control evolution with FLC algorithm for

various set points.

4.1.3 Temperature Control using Adaptive

Fuzzy Logic Controller

An analysis of the MSE in the last 40 iterations

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

472

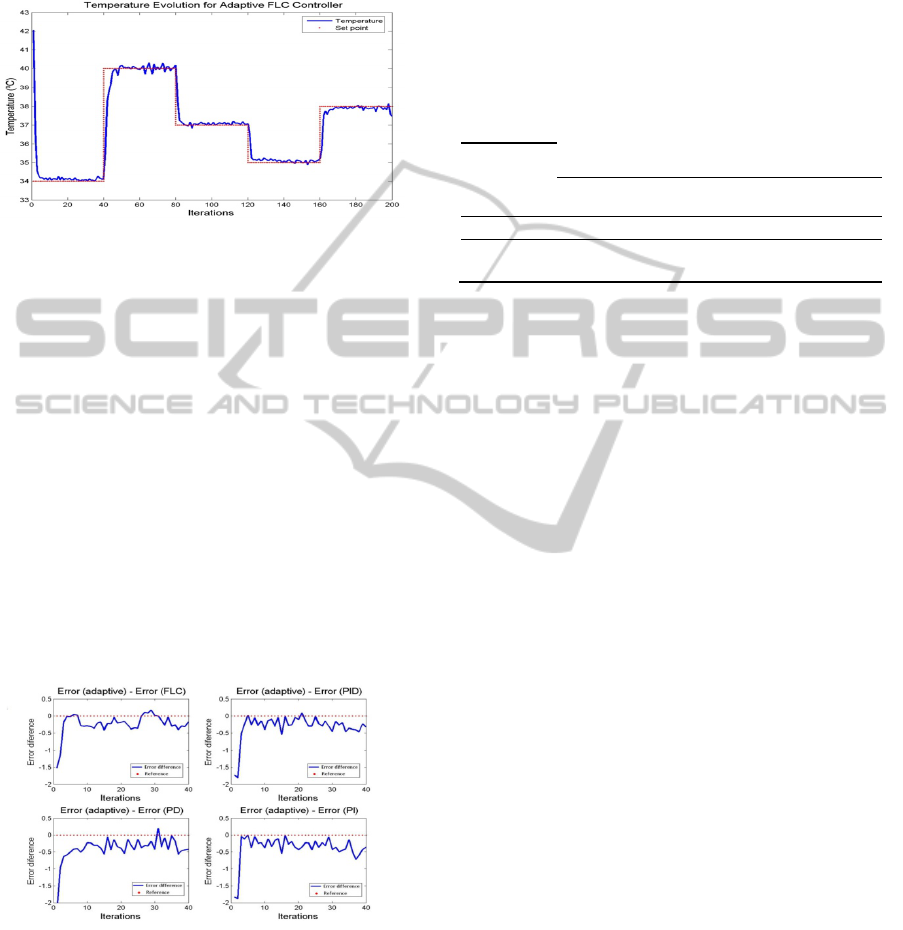
shows clearly the superiority of the latter compared

with others; the adaptive

algorithm has been able to

reduce the error to almost 50%. The MSE in this

case is 0.17.

Figure 7: Control evolution with adaptive FLC algorithm

for various set points.

4.2 Results Comparison

The graphical method consists in drawing the

representing curve of the difference between the

errors committed by two different algorithms at the

same time interval and to achieve the same set point,

i.e, represents the function defined as:

Error difference = E

(Algorithm 1)

- E

(Algorithm 2)

(4)

If E

(Algorihtm 1)

> E

(Algorithm 2)

Î Error difference > 0

The graphical representation of the function Error

difference is above zero.

If E

(Algorithm 1)

< E

(Algorithm 2)

Î Error difference < 0

The graphical representation of the function Error

difference is under zero.

Figure 8: Differences between the error committed by the

Adaptive FLC and the remaining algorithms.

The four cases presented in Fig. 8 show that the

error difference curve is almost always under the

zero line, mathematically this means that:

Error difference = E

(Algorithm 1)

- E

(Algorithm 2)

< 0

Î E

(Algorithm 1)

< E

(Algorithm 2)

In our case: E

(Algorithm 1)

is E

(Adaptive)

The Error difference is almost always less than

zero in the four cases, that means that the E

(Adaptive)

is less than the rest of committed errors by others

algorithms E

(FLC,PID,PD,PI)

The numerical comparison (Table 2) is based on the

analysis of the MSE for each algorithm.

Table 2: Comparative performance indices for all used

algorithms in real simulation.

MSE

Algorithms

PI PD PID

Classic

FLC

Adaptive

FLC

MSE

160

200

0.43 0.49 0.47 0.31 0.17

MSE

100

200

0.38 0.44 0.41 0.28 0.23

MSE

200

0.84 0.89 0.85 0.78 0.67

The results presented in this table show the

differences between the algorithms used. The

adaptive controller has the best error reduction

compared to the other, i.e., the adaptation presented

and tested by I. Rojas et.al (Rojas, 2006) is a good

alternative to replace the P, I, D controllers or a

classical fuzzy logic controller for these kinds of

plants.

4.3 The Perturbation Effects on the

behavior Algorithm

Fig. 9 depicts the behavior of the algorithms (static

FLC and Adaptive FLC) after a disturbance of 25%

at iteration number 20. The disturbance used here is

a simulation of a temperature decrease caused by a

secondary fan and at the 65 iteration, we have

caused a disturbance of 20% but this time we

simulate a temperature increase caused by another

source of temperature. The response of the plant

after the disturbances for each algorithm can clearly

explain the differences between every one of them.

Top of Figure 9 shows the behavior of static FLC

in perturbation cases. We can notice how these

disturbances can affect the control precision; the

static FLC keeps the plant under control but with

large error without over passing the perturbation

effects.

In the bottom graph the adaptive FLC presents a

very good performance against these disturbances. It

can be clearly noticed that the control precision does

not suffer big changes and that the adaptive

algorithm can overcome the perturbation effects in

few moments later.

Table 3 presents a numerical comparison

between the error committed in 10 iterations before

causing the disturbances and the error committed in

A NEW METHOTOLOGY FOR ADAPTIVE FUZZY CONTROLLER. COMPARISON PERFORMANCE AGAINST

SEVERAL CONTROL ALGORITHMS IN A REAL TIME CONTROL PROCESS

473

10 iterations with disturbance for each algorithm.

Figure 9: The perturbation effects on the control

performance.

Table 3: Comparative performance indices before and

after the perturbation.

MSE in 10 iterations

+ %25 in the

power of the Fan

- %20 in the power

of the Fan

FLC

Adapt

FLC

Adapt

FLC

Before perturbation

0.78 0.42 0.64 0.1

After perturbation

0.32 0.36 1.77 0.14

It is important to clear here that the error

reduction in the first case of perturbation doesn’t

mean a control improvement, it’s due to the new Fan

added by simulation, adding a Fan with power more

bigger signify big reduction in the error committed

and maybe the error will change the sign if this Fan

power was too much. The MSE presented in this

table proves that the perturbation effects on the

behavior of the adaptive algorithm are very small

when compared with their effects on the behavior of

the FLC algorithm.

5 CONCLUSIONS

This paper presents a comparative study between

several control algorithms and an adaptive fuzzy

logic controller. Both, the conventional fuzzy logic

controller and the P, I and D controller structure

show their capabilities to control the plant with a

reasonable error. The adaptive algorithm without

any off line pre-training and starting with no definite

rule base has been able to improve the committed

error during the control process. The adaptive

algorithm does not need any complex mathematical

models. It only needs a limited information from the

plant.The monotonicity and the delay of the plant,

were the only information used by the adaptive

algorithm to optimize the error at the plant output.

The results comparison can prove the superiority of

the proposed adaptive FLC controller against the

remaining of algorithms.

ACKNOWLEDGEMENTS

This work has been supported by the Genil Start-up

Project “Processing and Classification of Electro-

oculography (EOG) Data for Ataxia SCA-2

Diagnosis” (PYR-2010-23) from the CEI bioTIC

GENIL (CEB09-0010) of the CEI program from the

MICINN.

REFERENCES

Rojas, I., Pomares, H., González, J., Herrera, L. J., Guillen

,A., Rojas ,F., Valenzuela ,O., 2006. Adaptive fuzzy

controller: Application to the control of the tem-

perature of a dynamic room in real time, Fuzzy Sets

and Systems 157, 2241 – 2258.

Fan, X., Zhang, N., Teng, S., 2004. Trajectory planning

and tracking of ball and plate system using hierar-

chical fuzzy control scheme, Fuzzy Sets and Systems

144 (2) 297–312.

Hua, C., Guan, X., Duan, G., 2004. Variable structure ada-

ptive fuzzy control for a class of nonlinear time-delay

systems, Fuzzy Sets and Systems 148 (3) 453–468.

Lin, C. M., Hsu, C. F., 2004. Adaptive fuzzy sliding-mode

control for induction servomotor systems, IEEE Trans.

Energy Conversion 19 (2) 362–368.

Mamdani, E. H., Assilian, S., 1975. Experiment in

Linguistic Synthesis with a Fuzzy Logic Controller.

International Journal of Man-Machine Studies, 7, 1-

13.

Park, J.-H., Park, G.-T., Kim, S.-H., Moon, C.-J., 2005.

Output-feedback control of uncertain nonlinear

systems using a self-structuring adaptive fuzzy

observer, Fuzzy Sets and Systems 151 21–42.

Velagic, J., Vukic, Z., Omerdic, E., 2003. Adaptive fuzzy

ship autopilot for track-keeping, Control Eng. Practice

11 433–443.

Velez-Diaz, D., Tang, Y., 2004. Adaptive robust fuzzy

control of nonlinear systems, IEEE Trans. Systems,

Man Cybernetics, Part B 34 1596–1601.

Ziegler, J. G., Nichols, N. B., 1942. Optimum Settings for

Automatic Controllers, Trans. ASME, Vol. 64,759-

768.

Yi, J., Yubazaki, N., Hirota, K., 2002. A proposal of

SIRMs dynamically connected fuzzy inference model

for plural input fuzzy control, Fuzzy Sets and Systems

125 (1) 79–92.

Rojas, I., Pomares, H., Pelayo, F. J., Anguita, M., Ros, E.,

Prieto, A., 1999. New methodology for the develop-

pment of adaptive and self-learning fuzzy controllers

in real time, Int. J. Approx. Reason. 21, 109–136.

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

474