
MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK
WITH DETERMINISTIC INITIALIZATION
Vitaliy Kolodyazhniy
Department of Psychology, University of Salzburg, Hellbrunnerstrasse 34, 5020 Salzburg, Austria
Keywords: Multilayer perceptron, B-spline, Nonlinear synapse, Fuzzy rule, Deterministic initialization, Singular value
decomposition.
Abstract: A multilayer spline-based fuzzy neural network (MS-FNN) is proposed. It is based on the concept of
multilayer perceptron (MLP) with B-spline receptive field functions (Spline Net). In this paper, B-splines
are considered in the framework of fuzzy set theory as membership functions such that the entire network
can be represented in form of fuzzy rules. MS-FNN does not rely on tensor-product construction of basis
functions. Instead, it is constructed as a multilayered superposition of univariate synaptic functions and thus
avoids the curse of dimensionality similarly to MLP, yet with improved local properties. Additionally, a
fully deterministic initialization procedure based on principal component analysis is proposed for MS-FNN,
in contrast to the usual random initialization of multilayer networks. Excellent performance of MS-FNN
with one and two hidden layers, different activation functions, and B-splines of different orders is
demonstrated for time series prediction and classification problems.
1 INTRODUCTION
Multilayer perceptron (MLP) (Haykin, 1998) has
been perhaps the most popular neural network
architecture for more than two decades already due
to its universal approximation properties and ease of
practical implementation.
MLPs construct global approximations of
multivariate function data and are capable of
generalizing their response to regions of the input
space where little or no training data is present (Lane
et al., 1990). In such a way, MLP also avoids the
curse of dimensionality since the number of the
neurons of MLP depends only on the geometric
properties of the target function but not on the
dimension of the input space (Xiang et al., 2005;
Barron, 1992; Barron, 1993). However, the global
nature of the weight updating can be a disadvantage
for data with complex local structure. Furthermore,
the random initialization of MLP leads to quite
different results of training depending on the initial
weights, even with improved initialization
techniques (Nguyen and Widrow, 1990;
Lehtokangas et al., 1995; Erdogmus et al., 2005).
To add local properties to MLP approximations,
the Spline Net architecture was proposed (Lane et
al., 1990) in which the synaptic connections in form
of simple gains are replaced with nonlinear functions
constructed using B-splines. The authors of the
Spline Net presented the general concept of this
model and an example of a network with two layers,
linear B-splines, random initialization, and a
standard backpropagation algorithm.
In the present paper, we propose a generalized
model called ‘Multi-layer Spline-based Fuzzy
Neural Network’ (MS-FNN) with fully deterministic
initialization and more efficient training.
2 ARCHITECTURE
A Spline Net model (Lane et al., 1990) with
D
inputs,
L
layers, and
P
outputs can be defined as
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
∑
−
=
−
1
1
],1[],[][],[
)(
l
n
i
ilhl
i
lhl
ofo
σ
(1)
where
l
nh ,,1 …= , Ll ,,1 …
=
, Dn ≡
0
, Pn
L
≡ ,
],[ hl
o
is the output of neuron h in layer l,
h
hL
yo
ˆ
],[
≡
is the hth network output,
i
i
xo ≡
],0[
is the ith
network input,
1
]0,[
≡
l
o ,
][l
σ
is the sigmoid
activation function for layer l,
l
n is the number of
475
Kolodyazhniy V..
MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK WITH DETERMINISTIC INITIALIZATION.
DOI: 10.5220/0003652604750481
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 475-481
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
neurons in layer l, and
],[ hl
i
f is the nonlinear
synaptic connection function of input i of the hth
neuron in layer l:
∑
=
−−
=
l
m
j
hl
ji
ill
ji
ilhl
i
woof
1
],[
,
],1[][
,
],1[],[
)()(
μ
(2)
In (2),
][
,
l
ji
μ
is the jth receptive field function of
input i of layer l,
],[
,
hl
ji
w
is its synaptic weight in
neuron h, and
l
m is the number of receptive field
functions for each input of layer l. All receptive field
functions of a layer are shared between all neurons
of that layer.
Taking into account (2), we can re-write (1)
using a more compact vector-matrix notation:
)]([
]1[][][][][ −
=
lllll
oμWσo
,
Ll ,,1 …=
.
(3)
In (3),
T
nl
ll
l
oo ),,(
],[
]1,[][
…=o
is the vector of
outputs of layer
l ,
][l
σ is a vector activation
function of vector argument,
][l
W is a matrix of
synaptic weights in layer
l sized )(
1 lll
mnn
−
× , and
…),(),([)(
]1,1[][
2,1
]1,1[][
1,1
]1[][ −−−
=
llllll
oo
μμ
oμ
.)](,
],1[
][
,
1
1
T
nl
l
mn
l
ll
o
−
−
−
μ
…
A convenient choice for the receptive field
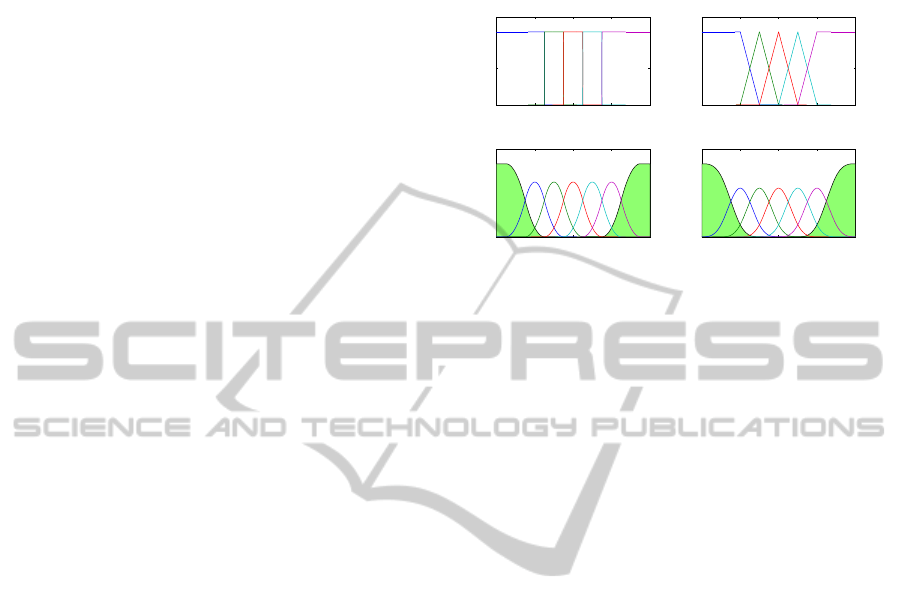
functions is B-splines due to their nice local
properties (Lane et al., 1990). To maintain a
partition of unity for any value of x, additional
marginal functions should be added at both ends of
the universe of discourse of x for splines of order>2
(see Fig.
1). As in (Lane et al., 1990, Bodyanskiy et
al., 2005, Kolodyazhniy, 2009, Kolodyazhniy et al.,
2007), we assume that the positions of knots of B-
splines are not optimized and are chosen
equidistantly.
B-splines in nonlinear synapses (2) can be
considered as membership functions of fuzzy sets
(Zhang, Knoll, 1998, Kolodyazhniy, 2009).
Therefore, the nonlinear synapses (2) can be
interpreted as elementary fuzzy inference systems
containing the following fuzzy rules:
.,,THEN
ISIF
],[
,
],[
]1,[
,
]1,[
][
,
],1[
ll
nl
ji
nl
i
l
ji
l
i
l
ji
il
wfwf
Oo
==
−
…
(4)
In (4),
][
,
l
ji
O is a fuzzy label such as ‘LARGE’,
‘MEDIUM’, ‘SMALL’, etc. determined by the
respective membership function
][
,
l
ji
μ
. Note that the
B-spline membership functions of order>2 are not
normal, i.e. the maximum values of non-marginal
functions are below one (see Fig. 1), such that the
partition of unity is always preserved.
−0.5 0 0.5 1 1.5
0
0.5
1
x
MF
Order=1
−0.5 0 0.5 1 1.5
0
0.5
1
x
MF
Order=2
−0.5 0 0.5 1 1.5
0
0.5
1
x
MF
Order=3
−0.5 0 0.5 1 1.5
0
0.5
1
x
MF
Order=4
Figure 1: B-spline membership functions (MF) of order 1
to 4 defined for variable ]1,0[
∈
x such that 5 membership
function are defined over the universe of discourse of
x
.
Shaded areas correspond to the marginal B-functions.
Denoting the sum of synaptic outputs of neuron
h in layer l as
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
∑
−
=
−
1
1
],1[],[],[
)
ˆ
(
l
n
i
ilhl
i
hl
yfa
(5)
we can define the following activation functions that
will be subsequently used:
],[],[][
)(:Identity
hlhll
aa =
σ
,
(6)
)]exp(1/[1)(:Sigmoid
],[],[][ hlhll
aa −+=
σ
(7)
.)exp(/)exp(
)(:Softmax
],[],[
],[][
∑
=
iLhL
hLL
aa
aσ
(8)
The original Spline Net model (Lane et al., 1990)
contained only sigmoid activation. A neuron with
linear B-splines (triangular membership functions)
and identity activation function coincides with the
neo-fuzzy neuron proposed in (Yamakawa et al.,
1992) and is used in (Bodyanskiy et al., 2005;
Kolodyazhniy et al., 2007) for constructing the two-
layered Neuro-Fuzzy Kolmogorov’s Network
(NFKN). Due to the generalization of the previously
developed NFKN model to multiple layers, we call
the neural net described in this paper ‘Multilayer
spline-based Fuzzy Neural Network’ (MS-FNN).
The architecture of MS-FNN (Fig. 2) is similar to
that of Spline Net except for the choice of activation
functions but the initialization and training
algorithms are different (see sections 3 and 4).
In case of two layers and the identity activation
functions, the MS-FNN architecture coincides with
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
476
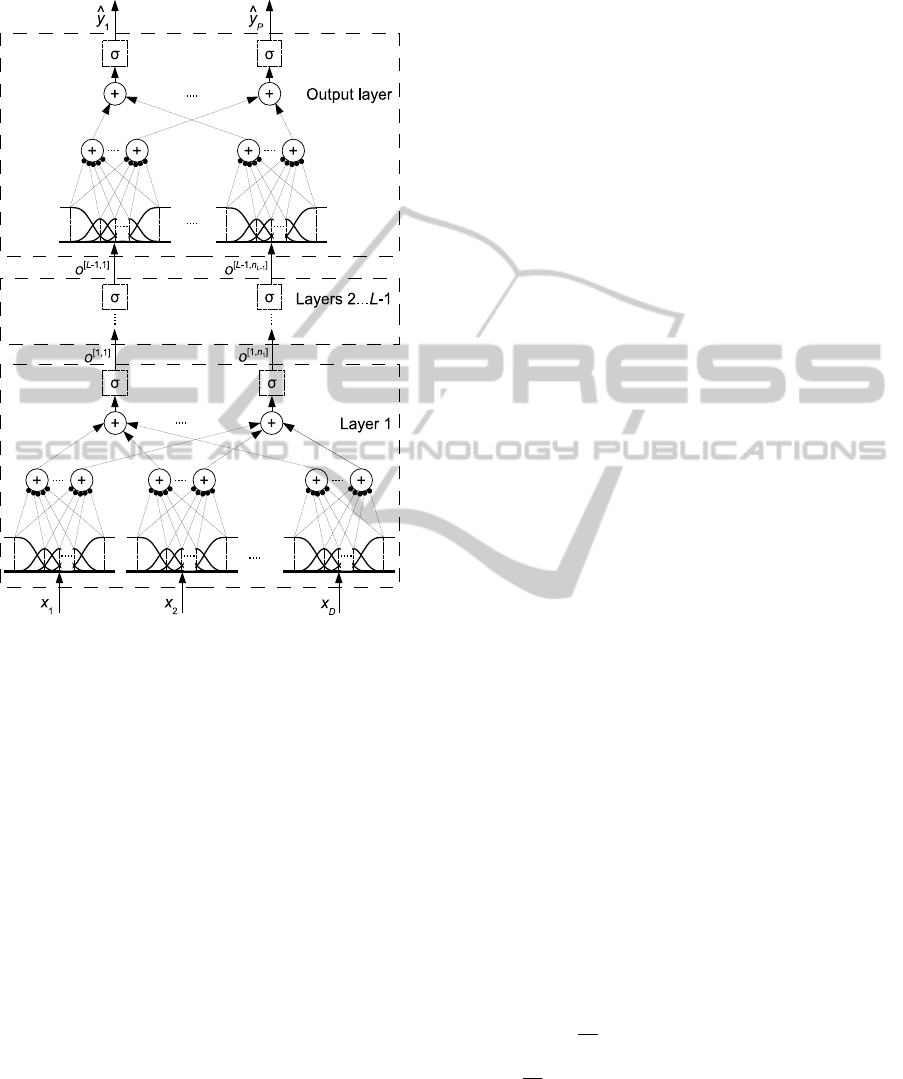
the Neuro-Fuzzy Kolmogorov’s Network (NFKN)
(Bodyanskiy et al., 2005; Kolodyazhniy, 2009).
Figure 2: MS-FNN architecture with
L
layers: dots (
•
)
represent synaptic weights, sigmoids (
σ
) are optional.
In contrast to MLP or Spline Net, the hidden
layers of MS-FNN may not contain sigmoid
activation functions at all because the required
nonlinear transformations can be performed by
nonlinear synapses. The sigmoid function should be
included in the output layer for binary classification
with the
cross-entropy error function.
For multinomial classification with cross-
entropy, the
softmax activation function in the output
layer is used (Bishop, 1995). The use of the sigmoid
in hidden layers is optional and should be decided
based on performance in a particular problem.
The MS-FNN model has a different structure
from the known B-spline-based neural networks (see
e.g. Coelho, Pessôa, 2009, Wang, Lei, 2001, Cheng
et al., 2001) and fuzzy systems (Zhang and Knoll,
1998) that are constructed of multidimensional basis
functions being
tensor products of univariate B-
splines. This approach is plagued by the
curse of
dimensionality
: the number of basis functions and
associated weights grows
exponentially with
increase of the input space dimension.
In contrast, MS-FNN relies on multilayer
superposition of univariate synaptic functions
constructed using B-splines thus avoiding the curse
of dimensionality similarly to MLP.
3 DETERMINISTIC
INITIALIZATION
Let us assume that the number of neurons in a layer
in MS-FNN does not exceed the total number of
membership functions in that layer, i.e.
lll
mnn ⋅≤
−1
(9)
This assumption is adequate for quite a wide
range of problems. It implies that the number of
neurons in a layer
l can be between one and
ll
mn ⋅
−1
where
1−l
n is the number of inputs of layer l and
Dn ≡
0
. For instance, in a network with ten inputs
and four membership functions per input the
maximum number of neurons in the first hidden
layer will be forty, which is sufficient in most cases.
Based on (9), the initialization of hidden layer
weights in MS-FNN can be performed
deterministically via linear PCA as proposed in
(Kolodyazhniy et al., 2007; Kolodyazhniy, 2009) for
the hidden layer of NFKN, such that all neurons in a
layer are initialized with mutually orthogonal weight
vectors. Here we generalize this approach to more
than one hidden layer.
Given a training data set containing
N patterns,
the PCA procedure is applied to the matrices of
membership degrees
[
]
T
lllll
N))((,)),1((
]1[][]1[][][ −−
= oμoμM … for all
hidden layers
1,,1
−
=
Ll …
successively, starting
from the first hidden layer with
T
D
xx ),,(
1
]0[
…== xo
. The vector of weights of the
hth hidden neuron in layer l corresponding to the hth
row of matrix
][l
W in (3) is assigned the transposed
hth loading (transposed hth column) from the matrix
V
found as a result of singular value decomposition
Tl
VΣUM =
][
(10)
where
][l
M
is equal to
][l
M
with mean values
subtracted column-wise.
After the
lth layer has been initialized, the input
data is propagated through layer
l, and the matrix of
membership degrees
]1[ +l
M
is computed followed
MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK WITH DETERMINISTIC INITIALIZATION
477

by weight initialization for layer
1+l using PCA as
described above. The output layer weights are
initialized with zeros.
If there is
only one neuron in a layer, its initial
weights for each nonlinear synapse (2) can be
chosen as linearly increasing, e.g. from zero to one.
During initialization of MS-FNN the
knots of B-
spline functions in the first hidden layer are set such
that the centers of the leftmost and the rightmost
non-marginal B-splines are assigned the minimum
and the maximum values of the corresponding
network input. The centers of B-splines between the
leftmost and the rightmost non-marginal functions
are distributed equally between them. The centers of
the marginal functions are set to the left and to the
right of the leftmost and the rightmost nonmarginal
functions, respectively, at the same distance as
between all the non-marginal functions.
If a
further hidden layer 1−l has sigmoidal
activation, then the centers of the non-marginal
membership functions of layer
l are distributed
equidistantly in the interval of
]1,0[
. Otherwise, the
minimum and maximum output values of all neurons
in layer
1−l
are computed and used for setting the
centers of membership functions in layers
l in the
same way as in the first layer. In such a way,
undesired saturations leading to neuron
underutilization and network paralysis during
training are avoided and the training is accelerated.
In case of sigmoid activation functions in layer
1
−
l ,
the knots of layer l should be positioned only once
during initialization such that the centers of the non-
marginal functions are distributed equidistantly in
the interval [0,1]. No knot re-positioning in layer l
during training is required because the preceding
neuron outputs are always in [0,1].
The entire initialization procedure is performed
layer by layer starting from the first hidden layer.
4 TRAINING
For regression, the error function is sum of squared
errors, and cross-entropy for classification.
For the both error functions described above, we
use resilient propagation (RPROP) which is a very
fast learning scheme (Riedmiller and Braun, 1993).
The weight update rule is without weight
backtracking (Rprop
–
, see Igel, C., Hüsken, M.,
2003) with the following parameters for MS-FNN:
5.0=
−
η
,
2.1=
+
η
,
6min
10
−
=Δ , 1.0
max
=Δ ,
1.0
0
=Δ .
To speed up batch training, the values of
membership functions in the first hidden layer of
MS-FNN are computed only once and then stored
throughout training because they do not change.
For layer l with identity activation in the
preceding layer 1
−
l , the B-spline knots are re-
positioned after each weight update with the RPROP
algorithm as in the initialization phase. This is done
to avoid saturations in synapses of the layer l,
because the outputs of layer
1−l are not limited to
the range of
]1,0[ in absence of a sigmoid activation
function. This knot re-positioning leads to a gradual
‘inflation’ of the distances between spline knots in
layer l following an approximately linear trend.
After training, the spline knots in each layer with
preceding identity activation can be re-set to their
initial positions with centers of non-marginal
functions between
]1,0[ , and the synaptic weights in
the preceding layer can be re-scaled to map the
respective neuron outputs onto
]1,0[ without
affecting the overall input-output mapping of the
MS-FNN model (Wang et al., 2009).
5 EXPERIMENTS
The MS-FNN model and the RPROP algorithm were
implemented in MATLAB v. 6.5 under Windows
XP on a PC with 2 GB of RAM and an Intel Core
Duo T2500 CPU with a 2.0 GHz clock. For
comparison, an MLP was implemented using the
MATLAB Neural Networks Toolbox with
modifications by the author for classification
problems which included the cross-entropy error
function. The MLP contained the hyperbolic tangent
activation function in hidden layers designated
below as ‘tanh’ in contrast to the ‘sigmoid’ (7) and
was trained with the same RPROP algorithm except
for two parameters:
50
max
=Δ and 07.0
0
=
Δ
(standard values of the MATLAB Toolbox).
The PCA initialization technique was used for
MS-FNN (except for the N-parity problem where
linear initialization was used, see section 3), while
the MLP was initialized randomly via the Nguyen-
Widrow algorithm (Nguyen and Widrow, 1990).
We report the best results and the training time,
although the latter might be biased in favor of the
MLP model because of the extensive code
optimization in the MATLAB Neural Network
Toolbox. It is expected that the training time for
MS-FNN can also be reduced via code optimization.
For MLP, the input data were standardized by
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
478

subtracting the mean value of the respective input
and dividing by its standard deviation which in all
cases resulted in a better performance of the MLP
compared to scaling onto the hypercube
D
]1,1[− . For
MS-FNN, the data were not transformed because the
membership functions of the input layer always
scale the data onto the unit hypercube.
5.1 Time SeriesPrediction
We compared the performance of MS-FNN and
MLP models in the forecasting of the well-known
Mackey-Glass (MG) time series (Mackey and Glass,
1977) for
17=
τ
. The error function was sum of
squared errors. The task was to predict the value of
the time series
)85( +tx using values
)(tx
, )6( −tx ,
)12( −tx , and )18( −tx as inputs for
3117...118=t
for training and
4117...3118=t
for testing.
First, an MS-FNN model with 2 hidden layers
with 10 neurons in each and one output neuron was
created and trained for 4000 epochs. For network
configuration and achieved prediction accuracy see
Table 1, where ‘W’ is the number of weights, ‘n’
and ‘m’ represent the number of neurons and
membership functions in the respective layers, and
‘Hid.Act’ and ‘Out.Act.’ stand for the activation
functions in the hidden and output layers,
respectively.
Then an MLP with two hidden layers with 30
neurons in each and one output neuron with a
number of parameters approximately equal to that of
MS-FNN was trained ten times for 10000 epochs
which took approximately the same time as the
training of MS-FNN. In Table 1 the best result out of
the ten runs is given (NRMSE Test=0.019) and is by
ca. 28% worse than that of MS-FNN (NRMSE
Test=0.0148).
5.2 Classification
For classification problems, all neural networks were
trained using the cross-entropy error functions. A
description of the data used for classification can be
found in Table 2. The target class variables had
values of 0 or 1 for both MS-FNN and MLP.
The N-Parity problem was solved for
20...2
=
N
with MS-FNN and for
13...2=N
with MLP. The
MS-FNN classifier contained two layers, each with
one neuron. In the hidden layer neuron all
membership functions were of first order, and of
second order in the output neuron. The number of
membership functions in the first layer neuron was
two per input, and
1+N
in the output neuron. With
this configuration, the network was able to solve the
N-parity problem without errors after only seven
epoch of training for any N between 2 and 20 (see
Table 3). Apparently, the scaling behavior of MS-
FNN would be the same also in higher dimensions.
For comparison, the N-parity problem was
solved for
13...2
=
N
using MLP with one hidden
layer containing N neurons which is the minimum
required for an MLP to converge in this problem
(Rummelhart and McClelland, 1986). The MLP was
trained for 1000 epochs. If no classification errors
were reached earlier, the training was stopped. For
each N, there were 10 runs, each with a different
random initialization. The results of the 10 runs were
averaged (see Table 4). For each N between 2 and
13, in at least 2 runs the training converged with no
classification errors. For
13=N
, the MLP’s shortest
training time (61.8s) was greater than that for MS-
FNN for
20
=
N
while the training set contained
128 times fewer patterns (8192 instead of 1048576)
and the number of inputs was 13 instead of 20.
To the author’s knowledge, this result for MS-
FNN is one of the very best reported so far in the
neural network community for the N-parity problem
in the dimension of the solved problem, network
size, and training time for a general-purpose neural
network, including (Wilamowski and Yu, 2010)
where N=16 was solved with a 9% success rate with
a fully connected MLP.
In the two spirals problem, the task was to find
the smallest network capable of classifying points
belonging to one of two intertwined spirals without
errors. Each of the two spirals had 97 points
(Wieland, 1988). For MS-FNN, exhaustive search
was performed for networks with one hidden layer
with one to eight neurons and
11...4
1
=m and
17...5
2
=m until a network able to classify the two
spirals without errors after up to 1000 epochs of
training was found. The search was done for linear,
quadratic, and cubic B-splines. As can be seen from
Table 3, the smallest MS-FNN had only two hidden
layer neurons with sigmoid activation, quadratic
splines in their synapses, and reached zero
classification errors after 384 epochs of training.
For MLP, a search for the smallest architecture
capable of classifying the two spirals without errors
was done for architectures with two hidden layers
each containing n neurons for
10...6=n
and 100
runs of up to 10000 epochs of training for each n. As
can be seen from Tables 3 and 4, the MS-FNN
model had approximately three times fewer
parameters (48 vs. 151) and converged much faster
than MLP.
MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK WITH DETERMINISTIC INITIALIZATION
479
For the same data with 194 points training with
RPROP 1500 to 15000 epochs were reported for a
four-layered perceptron-like network with additional
shortcut connections (Riedmiller and Braun, 1993).
The UCI Letter data set (see UCI) is a larger-
sized multinomial classification problem. The MS-
FNN model providing the highest classification
accuracy had one hidden layer with identity
activation and 38 neurons, and 26 neurons in the
output layer. The search was done among
architectures with one hidden layer with 16 to 40
neurons with cubic splines in their synapses with
and without sigmoid activation in the hidden layer.
For comparison, MLPs with two hidden layers
containing 70, 80, 90, and 100 neurons in each of the
hidden layers were tested 10 times for each
configuration with different random initializations.
Both the MS-FNN and MLP models were trained for
500 epochs. The training was stopped earlier if all
patterns in the training set were classified correctly.
As can be seen from Tables 3 and 4, the MS-FNN
model provided a slightly lower error for the test
data (4.1% vs. 4.225%) with fewer weitghts. Both of
these results rank among the very best achieved for a
single neural network. E.g., in (Schwenk and
Bengio, 2000) a testing error of 6.1% is reported for
a single MLP on the same dataset, and for ensembles
it was 4.3% for bagging and 1.5% for boosting, the
latter being the best result known to the author.
6 Conclusions
A practical implementation of a multilayer spline-
based fuzzy neural network (MS-FNN) with
improved local properties and deterministic
initialization was presented and improved
performance of the proposed model was
demonstrated in comparison with a conventional
multilayer perceptron.
The deterministic initialization of the MS-FNN
model, among other advantages, makes a direct
structure optimization of the neural network
possible, even using a straightforward exhaustive
search approach, because the number of parameters
determining the structure (the number of neurons
and membership functions) is small and the possible
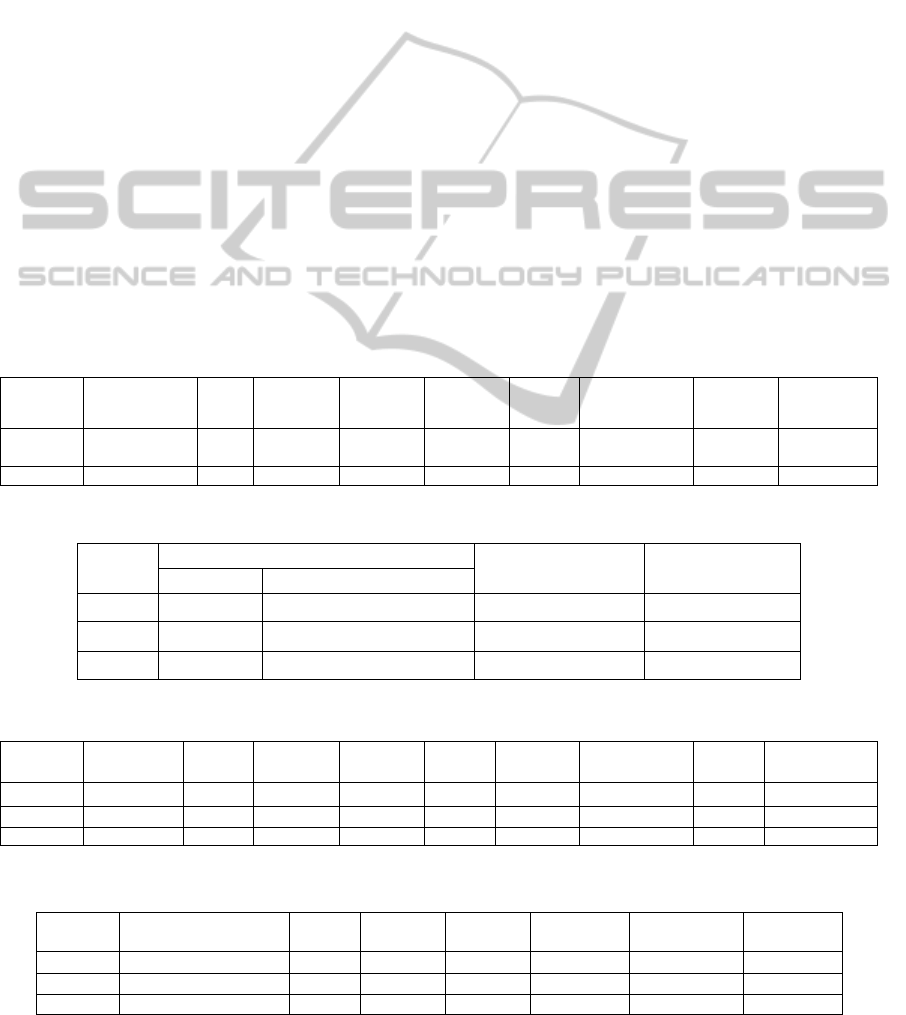
Table 1: Results of prediction of the Mackey-Glass time series 85 steps ahead.
Model
NRMSE Train,
Test
W Hid. act. Out. act. n m Spline order Epochs
Training
time, s
MS-FNN
0.0142,
0.0148
1090 sigmoid identity 10, 10, 1 7, 7, 11 4, 4, 4 4000 910.2
MLP 0.0181, 0.019 1111 tanh identity 30, 30, 1 – – 10000 902.6
Table 2: Datasets used for classification.
Dataset
Number of patterns
Number of attributes Number of classes
Training Testing
N-parity 4...1048576 – 2...20 2
Spirals 194 – 2 2
Letter 16000 4000 16 26
Table 3: Classification results with MS-FNN. For N-parity, results for
20...2
=
N
are shown.
Dataset
Error, %
Train, Test
W Hid. act. Out. act. n m Spline order Epochs
Training time,
s
N-parity 0, – 7...61 identity sigmoid 1, 1 2, 3...21 1, 2 7 0.16...44.4
Spirals 0, – 48 sigmoid sigmoid 2, 1 4, 16 3, 3 384 7.07
Letter 0.13, 4.1 12540 identity softmax 38, 26 6, 9 4, 4 500 2123.3
Table 4: Classification results with MLP. For N-parity, results are average of 10 runs for
13...2=N
.
Dataset Error, % Train, Test W Hid. act. Out. act. n Epochs
Training
time, s
N-parity 0.078...12.5, – 9...196 tanh sigmoid 2...13, 1 148.9...941.2 0.5...61.8
Spirals 0, – 151 tanh sigmoid 10, 10, 1 5743 28.4
Letter 0, 4.225 14426 tanh softmax 100, 100, 1 303 792.5
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
480

values of these parameters are natural numbers with
quite a limited range. For a particular combination of
these parameters the mapping realized by the neural
network is deterministic for the given training
algorithm and the number of training epochs.
Future research of the author would include the
development of more efficient algorithms for
structure optimization, as well as the improvement
of interpretability of fuzzy rules for knowledge
extraction from the trained net.
REFERENCES
Haykin, S., 1998. Neural Networks: A Comprehensive
Foundation, Prentice Hall, Upper Saddle River, 2nd
edition.
Lane S. H., Flax, M. G., Handelman, D. A., Gelfand, J. J.,
1990. Multi-Layer Perceptrons with B-Spline Rece-
ptive Field Functions. In Advances in Neural
Information Processing Systems, R. P. Lippman, J.
Moody, D. S. Touretzky (Eds.), Vol. 3,. Morgan
Kaufman, San Francisco, pp. 684-692.
Xiang, C., Ding, S. Q., Lee, T.H., 2005. Geometrical In-
terpretation and Architecture Selection of MLP. IEEE
Transactions on Neural Networks, 16, 84-96.
Barron, A. R., 1992. Neural Net Approximation, In Pro-
ceedings of the 7th Yale Workshop Adaptive and
Learning Systems, New Haven, CT, 1992, pp. 69–72.
Barron, A. R., 1993. Universal Approximation Bounds for
Superpositions of a Sigmoidal Function. IEEE Tran-
sactions on Information Theory, 39, 930–945.
Nguyen, D., Widrow, B., 1990. Improving the Learning
Speed of 2-layer Neural Networks by Choosing Initial
Values of the Adaptive Weights. In Proceedings of the
International Joint Conference on Neural Networks,
vol. 3, 1990, pp. 21–26.
Lehtokangas, M., Saarinen, J., Kaski, K., Huuhtanen, P.,
1995. Initializing Weights of a Multilayer Perceptron
Network by Using the Orthogonal Least Squares
Algorithm. Neural Computation, 7, 982-999.
Erdogmus, D., Fontenla-Romero, O., Principe, J. C.,
Alonso-Betanzos, A., Castillo, E., 2005. Linear-Least-
Squares Initialization of Multilayer Perceptrons
Through Backpropagation of the Desired Response.
IEEE Transactions on Neural Networks, 16, 325-337.
Bodyanskiy, Ye., Gorshkov, Ye., Kolodyazhniy, V.,
Poyedyntseva, V., 2005. Neuro-fuzzy Kolmogorov’s
Network, Lecture Notes in Computer Science, W.
Duch et al. (Eds.), Vol. 3697, Springer, Berlin,
Heidelberg, New York, pp. 1-6.
Kolodyazhniy, V., 2009. Spline-based Neuro-fuzzy
Kolmogorov’s Network for Time Series Prediction. In
Proceedings of the 17th European Symposium on
Artificial Neural Networks (ESANN 2009), Bruges,
Belgium, 2009, pp. 153-158.
Kolodyazhniy, V., Klawonn, F., Tschumitschew, K., 2007.
A Neuro-fuzzy Model for Dimensionality Reduction
and its Application. International Journal of
Uncertainty, Fuzziness, and Knowledge-Based
Systems, 15, 571-593.
Zhang, J., Knoll, A., 1998. Constructing Fuzzy Controllers
with B-Spline Models — Principles and Applications.
International Journal of Intelligent Systems, 13, 257-
285.
Yamakawa, T., Uchino, E., Miki, T., Kusanagi, H., 1992.
A Neo Fuzzy Neuron and its Applications to System
Identification and Prediction of the System Behavior,
In Proceedings of the 2nd International Conference on
Fuzzy Logic and Neural Networks (IIZUKA-92),
Iizuka, Japan, 1992, pp. 477-483.
Bishop, C. M., 1995. Neural Networks for Pattern
Recognition, Clarendon Press, Oxford.
Coelho, L. d. S., Pessôa, M. W., 2009. Nonlinear
Identification Using a B-Spline Neural Network and
Chaotic Immune Approaches. Mechanical Systems
and Signal Processing, 23, 2418-2434.
Wang, K., Lei, B., 2001. Using B-spline Neural Network
to Extract Fuzzy Rules for a Centrifugal Pump
Monitoring. Journal of Intelligent Manufacturing, 12,
pp. 5-11.
Cheng, K. W. E., Wang, H. Y., Sutanto, D., 2001.
Adaptive Directive Neural Network Control for Three-
Phase AC/DC PWM Converter, Proc. Inst. Electr.
Eng.—Elect. Power Appl., vol. 148, no. 5, pp. 425–
430.
Riedmiller, M., Braun, H., 1993. A Direct Adaptive
Method for Faster Backpropagation Learning: The
Rprop Algorithm. Proceedings of the IEEE
International Conference on Neural Networks, 1993,
pp. 586-591.
Igel, C., Hüsken, M., 2003. Empirical Evaluation of the
Improved Rprop Learning Algorithms.
Neurocomputing, 50, 105-123.
Wang, D., Zeng, X.-J., Keane, J. A., 2009. Intermediate
Variable Normalization for Gradient Descent Learning
for Hierarchical Fuzzy System. IEEE Transactions on
Neural Networks, 17, 468-476.
Mackey, M. C., Glass, L., 1977. Oscillation and Chaos in
Physiological Control Systems. Science, 197, 287-289.
Rumelhart, D. E., McClelland, J. L., 1986. Parallel
Distributed Processing vol. 1, Cambridge, MIT press.
Wilamowski, B.M., Yu H., 2010. Improved Computation
for Levenberg–Marquardt Training. IEEE
Transactions on Neural Networks, 21, 930-937.
Wieland, A., 1988. Two spirals.
http://www.boltz.cs.cmu.edu/benchmarks/two-
spirals.html. CMU Repository of Neural Network
Benchmarks.
UCI Machine Learning Repository. http://archive.ics.uci.
edu/ml/index.html
Schwenk, H., Bengio, Y., 2000. Boosting Neural
Networks. Neural Computation, 12, 1869–1887.
MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK WITH DETERMINISTIC INITIALIZATION
481
