NETWORK CLUSTERING BY ADVANCED LABEL

PROPAGATION ALGORITHM

Krista Rizman Žalik and Borut Žalik

Faculty of Electrical Engineering and Computer Science, University of Maribor, Maribor, Slovenia

Keywords: Clustering, Community detection, Network, Graph, Modularity.

Abstract: Real time community detection is enabled by recently proposed linear time – O(m) on a network with m

edges – label propagation algorithm (LPA). LPA finds only local maxima in modularity space. To escape

local maxima, we propose LPA* that propagate label of a neighbour node having the most common

neighbours in the case when multiple neighbour labels are equally frequent and use multistep try of

propagation of each neighbour label in the case when multiple neighbour labels are equally frequent in two

successive iterations. Experiments show that LPA* detects communities with high modularity values. LPA*

propagation is more stable and improves detection of natural communities while it retains high scalability

and simplicity of label propagation.

1 INTRODUCTION

The large-scale online social networks require the

new and fast computational techniques for their

analysis. Beside social networks, many other

complex networks have recently developed:

collaboration networks, the internet, the World-

Wide-Web, biological networks and transport

networks.

Important property of networks is their community

structure: nodes gathered into distinct groups called

clusters or communities. Detecting communities in

networks is important task that provides insight into

the complex structure and functional units of real-

world systems. A community in a network is a group

of nodes that are similar to each other and dissimilar

from the rest of the network. A community is a

group of nodes where nodes are densely

interconnected and sparsely connected to other parts

of a network. A network can be represented by a

graph. Partitioning of the vertex set of a graph into

disjoint subsets called clusters or communities is

graph clustering.

Network data sets become larger and larger.

Therefore the speed of community detection

algorithms becomes more and more important.

Several different approaches have been proposed to

find community structures in networks; reviews of

the various methods present in the literature can be

found (Forutnato, 2010).

The detection of community structure in a

network can be performed by mapping the network

into a tree known as dendogram. Leaves of the tree

are nodes that are joined by branches into bigger and

bigger clusters and communities and so forming a

hierarchy of communities. It is neccessary to

measure the goodness of partitioning at each step of

hierarchical clustering otherwise hierarchical

algorithms would continue with clustering until

every node is split into a single community or all

nodes are joined into one community. To measure

the goodnes of particular clustering of network into

communities, Newman introduced measure called

modularity Q (Eq.1) and proposed hirarchical

aglomerative algorithm with time complexity O(m d

log n), where d is the depth of dendogram, n number

of nodes and m number of edges (Newman, Girvan,

2004).

Consider a undirected and unweigted network of

n nodes and m edges represented by an adjacency

matrix A, with elements A

equal to 1 if there is a

link between node u and v and 0 otherwise. This is

described by 



, 





Kronecker’s delta and degree

of node u is described by



. Modularity essentially

measures the actual fraction of intra-community

edges minus expected value in null model, where

connections are made randomly and division model

is the same. Modularity Q is defined:

(1)

where 



is probability in the null model that an

444

Rizman Žalik K. and Žalik B..

NETWORK CLUSTERING BY ADVANCED LABEL PROPAGATION ALGORITHM.

DOI: 10.5220/0003656104360439

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 436-439

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

edge exists between node u and v. We can define

modularity matrix B with elements: 



=



−





, then modularity is:

(2)

And modularity is addition of contributions over

all communities 



(3)

where 



is the number of intra-community edges

that have both ends in community t and 



 is the

number of outgoing edges that have only one end in

community t.

Among the many clustering techniques for

network data now available (see Fortunato, 2010 for

review) the methods of modularity maximization are

the most popular.

Recently Raghavan et al (Raghavan et al., 2007)

proposed a near linear time algorithm to detect

comunities named label propagation algorithm

(LPA). Bare and Clark (Baber and Clark 2009)

extended LPA and introduce LPAm algorithm that

maximizes modularity measure of community

quality.

2 LPA, LPAM

The LPA algorithm is based on a simple idea.

1. Each node is associated by a label, which is an

integer identifier. At the beginning each node is

initialized with unique label. Then the label can

change in many iteration steps.

2. Nodes sequentially update their labels. Vertices

order in label updating proces is random.

3. New label of each node is the most frequent label

among its neighbours. The label updating rule for

node x is :

(4)

If more than one label is the most frequent ones,

then the new label is chosen randomly. This occurs

usually in the beginning of label propagation. The

propagation step is performed iteratively until all

vertices have labels that do not change any more. At

the end, nodes with the same label forms cluster or

community.

The label propagation offers less expensive

computation as possible – it has linear time

complexity. The weaknesses are that LPA is not

stable and that the algorithm is sensitive to the order

of nodes that are updated. Therefore solutions can be

different in different runs. Sometimes LPA may

even end with trivial solution where only one

community is identified.

Baber and Clark extended LPA by modifying

the label updating rule so that modularity can be

maximized and their proposed method LPAm use

the following updating rule for node x:

(5)

3 LPA*

At first, we show examples where LPA and LPAm

gets stuck in a local maximum on an example

network (see Figures 1, 2a) similar to example

network used by Liu and Murata (Liu and Murata

2010), who employed greedy agglomerative

algorithm for merging identified communities by

LPA algorithm and so extend LPA to advanced

modularity specialized label-propagation algorithm

LPAm+.

Take an example network from Figure 1. It can

be intuitively divided into two clusters. LPA can

partition this example network into four clusters

(Figure 2a) or even one cluster as a result of

propagation iterations as shown in Figure 1.

The first problem of label propagation

algorithms are large communities as a result of

epidemic nature of the algorithm and the second is

that the label propagation is prone to get stuck in

local maximum.

To escape from formation of large communities

as result of the epidemic nature of LPA algorithm as

shown in Figure 1, we must solve a major limitation

where one node-label spread over large amount of

nodes by using random choose of label in the case

when all neighbour label are equal frequent. The

reason is in initial formation of communities or in

networks, where some communities do not have

strong enough links to prevent foreign communities

to spread through.

To escape the local maximum as shown in an

example network in Figure 2.a we must try to

continue with label propagation and searching for

new maximum (Figures 2.b,2.c)..

The LPA* algorithm uses two extensions to LPA:

1. Instead of random choose of neighbour label in

the case where there is more than one most frequent

neigbour lables for current vertex, we choose a label

having more common neigbours with current vertex.

2. To escape from local minimum we continue with

NETWORK CLUSTERING BY ADVANCED LABEL PROPAGATION ALGORITHM

445

propagation so that in each iteration we choose one

different label from a set of most frequent labels in

the case that remains more maximal neighbour

labels in two succesive iterations (see Figures 2.a,

2.b,2.c).

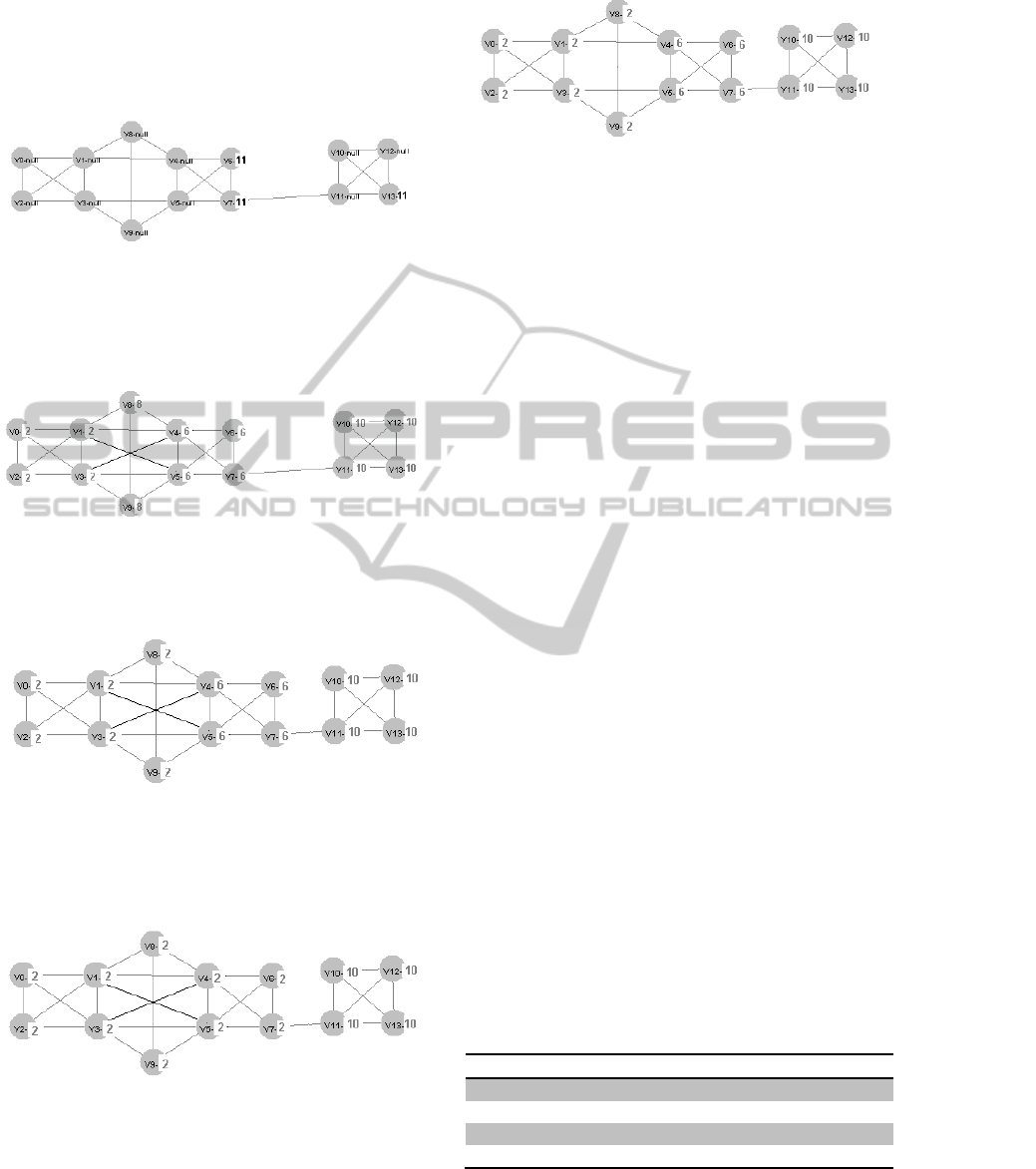
Figure 1: An example network. Vertex v7 has four

neighbours connected with one edge (v4, v6, v5, v11).

With choosing label 11 for propagation to v7 and with

choosing label 11 for vertices v6 and v13, the propagation

ends with bad clustering partition having one cluster.

Figure 2a: Similar example network as in Figure 1 that can

be intuitively partitioned into two communities. LPA and

LPAm gets stuck in a poor local maximum where network

is partitioned into four communities with labels: 2,6,8,10.

Figure 2b: LPA* algorithm escape the local maximum

shown in Figure 2.a by choosing the next neighbour label

(2) for propagation in vertex v9, because although 8 is

picked for propagation in the previous step (Figure 2a),

there remains multiple maximal labels (2,6,8).

Figure 2c: After continuing and finishing label

propagation by LPA* from Figure 2b, we climb to global

maximum.

Figure 3: The similar network as in Figure 2 where LPA*

finds solution with tree clusters with modularity 0.45 that

is global maximum, while partition with two clusters has

modularity 0.38.

Algorithm LPE* for label propagation clustering

of graph with n vertices and m edges is simple:

for ll=1,…,n

assign label ll to vertex ll

repeat

for v=1,…,n

if there is one most frequent neigbour label

assign most frequent neigbour label to vertex v

else

if in the previous step is only one most frequent label

assign label of neigbor vertex v1 that has the greatest

number of common neigbours with current vertex v

else

assign randomly one of the most frequent neigbours

label that has not been assigned

until there is no changes of labels

4 EXPERIMENTS

We tested LPA* for clustering of several real-world

networks: the karate club network - Karate club

(Zackary, 1977), the dolphin association network -

Dolphins (Lusseau et al., 2003), the network of co-

published political books - Political Books (Krebs,

2008) and the network of co-authorships for e-print

papers posted to the condensed matter archive -

Condomat2003 (Newman, 2004). Used real-world

networks have different number of edges and nodes

(see Table 1). We treated all networks as undirected

and unweighted.

Table 1: The number of edges and nodes of real-world

networks used in our experiment.

Network No. of nodes No. of edges

Karate Club 34 78

Dolphins 62 159

Political Books 105 441

Condomat 2003 27519 116181

Experiments show that LPA* outperform LPA in

quality measured by modularity of detected

communities and in two examples also LPAm,

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

446

which is more computational complex (Table 2).

Table 2: Comparison between LPA, LPAm and LPA*.

Values are collected from twenty runs for each network.

max

denotes maximal modularity, Q

avg

denotes the

average modularity.

LPA

Network Q

max

Karate Club 0,415 0,366

Dolphins 0,523 0,484

Political Books 0,519 0,481

Condomat 2003 0,622 0,607

LPAm

Network

max

Karate Club 0,40 0,347

Dolphins 0,515 0,495

Political Books 0,522 0,493

Condomat 2003 0,594 0,582

LPA*

Network

max

Karate Club 0,367 0,350

Dolphins 0,519 0,488

Political Books 0,489 0,483

Condomat 2003 0,598 0,588

Table 3: Comparison of standard deviations between

LPAm and LPA*.

Network

 LPAm ) LPA*)

Karate Club 0,027 0,011

Dolphins 0,007 0,033

Political Books 0,02 0,014

Condomat 2003 0,004 0,004

Authors of LPA algorithm describe that the number

of label propagation steps required by LPA

algorithm to converge is independent of number of

nodes and after 5 steps 95% of the nodes can be in

the right community. Table 4 shows the actual

values of number of iterations obtained from running

LPA* twenty times for used real-world networks.

Table 4: The average number of label propagation steps

required for the LPA* to converge. Values are averaged

over twenty runs in each of the real-world networks.

Network Number of steps

Karate Club 3,2

Dolphins 5,3

Political Books 5,2

Condomat 2003 5,6

5 CONCLUSIONS

In this paper we propose LPA* algorithm based on

the previously proposed LPA algorithm. LPA*

algorithms try to continue with propagation and

drive out of local maxima that stops LPA and

improved LPAm algorithms.

Experiments show that LPA* outperforms

algorithm in quality measured by modularity of

detected communities LPA and LPAm.

Another important property is that the identified

communities in different runs are not distinct very

much. This is property more obvious for bigger

networks. Open problem for future work remains

how to make the algorithm complete deterministic.

ACKNOWLEDGEMENTS

The authors wish to thank (anonymous) reviewers.

The work has been supported by the Slovene

Research Agency within the program P2-0041.

REFERENCES

Baber, M. J., Clark, J. W., Detecting newtork communities

by propagating labels under constraints, Phys. Rev. E

80 (2009) 026129.

Clauset, A., Newman, M. E. J., Moore C., Finding

community’s structure in very large networks, Physc.

Review, E 70 (2004) 066111.

Guimera, R., Armal A. N, Functional cartography of

complex metabolic networks, Nature 433 (2005)

859-900.

Fortunato, S., Community detection in graphs, Physics

Reports 486, 75/174 (2010).

Krebs, A. network of co-published books about us politics

sold by the online bookseller (2008),

http://www.orgnet.com

Lusseau, D, Schneider K., boisseau, O. J., Haase P.,

Slooten E., Dawson, S. M., The bottlenose dolphin

community of doubtful sound features a large

proportion of long-lasting associations, behavioural

Ecology and Sociology 54 (2003) 396-405.

Liu, X., Murata T, Advanced modularity-specialized label

propagation algorithm for detecting communities in

networks, Physica A, mar.2010.

Newman, M. E. J., Girvan, M., Finding and evaluating

community structures in large networks, Phys.rev. E

70 (2004) 026113.

Newman, M. E. J., Fast algorithm for detecting

community structure in networks, Phys. Rev., E 69

(2004) 066133.

Newman, M. E. J., Modularity and community structure in

networks, Proc. Natl, Acad. Sci. (2006) 8577-8582.

Raghavan, U. N., Albert, R., Kumara, S., Near linear

algorithm to detect community structures in

large/scale networks, Phys. Rev. E 76 (2007) 036106.

Zachary, W. W., An information flow model for conflict

and fission in small group, Journal of Antropological

research 33 (1977) 452-473.

NETWORK CLUSTERING BY ADVANCED LABEL PROPAGATION ALGORITHM

447