
A NOVEL SUPERVISED TEXT CLASSIFIER FROM A SMALL
TRAINING SET
Fabio Clarizia, Francesco Colace, Massimo De Santo, Luca Greco and Paolo Napoletano
Department of Electronics and Computer Engineering, University of Salerno
Via Ponte Don Melillo 1, 84084 Fisciano, Italy
Keywords:
Text classification, Term extraction, Probabilistic topic model.
Abstract:
Text classification methods have been evaluated on supervised classification tasks of large datasets showing
high accuracy. Nevertheless, due to the fact that these classifiers, to obtain a good performance on a test set,
need to learn from many examples, some difficulties may be found when they are employed in real contexts.
In fact, most users of a practical system do not want to carry out labeling tasks for a long time only to obtain a
better level of accuracy. They obviously prefer algorithms that have high accuracy, but do not require a large
amount of manual labeling tasks.
In this paper we propose a new supervised method for single-label text classification, based on a mixed Graph
of Terms, that is capable of achieving a good performance, in term of accuracy, when the size of the training
set is 1% of the original. The mixed Graph of Terms can be automatically extracted from a set of documents
following a kind of term clustering technique weighted by the probabilistic topic model. The method has been
tested on the top 10 classes of the ModApte split from the Reuters-21578 dataset and learnt on 1% of the
original training set. Results have confirmed the discriminative property of the graph and have confirmed that
the proposed method is comparable with existing methods learnt on the whole training set.
1 INTRODUCTION
The problem of text classification has been exten-
sively treated in literature where metrics and mea-
sures of performance have been reported (Christopher
D. Manning and Schtze, 2009), (Sebastiani, 2002),
(Lewis et al., 2004). All the existing techniques have
been demonstrated to achieve high accuracy (mainly
assessed through the F
1
measure) when employed in
supervised classification tasks of large datasets.
Nevertheless, it has been found that only 100 doc-
uments could be hand-labeled in 90 minutes and in
this case the accuracy of classifiers (amongst which
we find Support Vector Machine based methods),
learnt from this reduced training set, could be around
30%. This makes, most times, a classifier unfeasible
in a real context. In fact, most users of a practical
system do not want to carry out labeling tasks for a
long time only to obtain better level of accuracy. They
obviously prefer algorithms that have high accuracy,
but do not require a large amount of manual labeling
tasks (McCallum et al., 1999)(Ko and Seo, 2009). As
a consequence, we can affirm that, in several applica-
tion fields we need algorithms to be fast and with a
good performance.
Here we propose a linear single label supervised
classifier that is capable, based on a vector of features
represented through a mixed Graph of Terms (mGT ),
of achieving a good performance, in terms of accu-
racy, when the size of the training set is 1% of the
original and comparable to the performances achieved
by existing methods learnt on the whole training set.
The vector of features can be automatically ex-
tracted from a set of documents following a kind of
term clustering technique weighted by the probabilis-
tic topic model. The graph learning procedure is com-
posed of two stages and leads us to a two level repre-
sentation. Firstly, we group terms with a high degree
of pairwise semantic relatedness so obtaining several
groups, each of them represented by a cloud of words
and their respective centroids that we call concepts. In
this way, we obtain the lowest level, namely the word
level. Later, we compute the second level, namely
the conceptual level, by inferring semantic related-
ness between centroids, and so between concepts.
To confirm the discriminative property of the
graph we have evaluated the performance through a
comparison between our term extraction methodol-
545
Clarizia F., Colace F., De Santo M., Greco L. and Napoletano P..
A NOVEL SUPERVISED TEXT CLASSIFIER FROM A SMALL TRAINING SET.
DOI: 10.5220/0003661105370545
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (SSTM-2011), pages 537-545
ISBN: 978-989-8425-79-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

ogy and a term selection methodology which con-
siders the vector of features formed of only the list
of concepts and words composing the graph and so
where relations have not been considered. The re-
sults, obtained on the top 10 classes of the ModApte
split from the Reuters-21578 dataset, show that our
method, independently of the topic, is capable of
achieving a better performance.
2 PROBLEM DEFINITION
Following the definition introduced by (Sebastiani,
2002), a supervised Text Classifier may be formal-
ized as the task of approximating the unknown target
function Φ : D × C → {T, F} (namely the expert) by
means of a function
ˆ
Φ : D × C → {T, F} called the
classifier, where C = {c
1
, ..., c
|C|
} is a predefined set
of categories and D is a (possibly infinite) set of doc-
uments. If Φ(d
j
, c
i
) = T , then d
j
is called a positive
example (or a member) of c
i
, while if Φ(d
j
, c
i
) = F it
is called a negative example of c
i
. Moreover, the cat-
egories are just symbolic labels: no additional knowl-
edge (of a procedural or declarative nature) of their
meaning is usually available, and it is often the case
that no metadata (such as e.g. publication date, doc-
ument type, publication source) is available either. In
these cases, classification must be accomplished only
on the basis of knowledge extracted from the docu-
ments themselves.
In practice we consider an initial corpus Ω =
{d
1
, . . . , d
|Ω|
} ⊂ D of documents pre-classified under
C = {c
1
, ..., c
|C|
}. The values of the total function Φ
are known for every pair (d
j
, c
i
) ∈ Ω × C.
We consider the initial corpus to be split into two
sets, not necessarily of equal size:
1. training set Tr = {d
1
, . . . , d
|Tr|
}. The classifier Φ
for categories is inductively built by observing the
characteristics of these documents;
2. test set Te = {d
|Tr|+1
, . . . , d
|Ω|
}, used for testing
the effectiveness of the classifiers.
We assume that the documents in Te cannot partici-
pate in any way in the inductive construction of the
classifiers.
Here we consider the case of single-label classifi-
cation, also called binary, in which, given a category
c
i
, each d
j
∈ D must be assigned either to c
i
or to
its complement c
i
. In fact, it has been demonstrated
that the binary case is more general than the multi-
label (Sebastiani, 2002; Christopher D. Manning and
Schtze, 2009). It means that we consider the classi-
fication under C = {c
1
, ..., c
|C|
} as consisting of |C |
independent problems of classifying the documents
in D under a given category c
i
, and so we have
ˆ
φ
i
,
for i = 1, . . . , |C|, classifiers. As a consequence, the
whole problem in this case is to approximate the set
of function Φ = {φ
1
, . . . , φ
|C|
} with the set of |C | clas-
sifiers
ˆ
Φ = {
ˆ
φ
1
, . . . ,
ˆ
φ
|C|
}.
2.1 Data Preparation
Texts cannot be directly interpreted by a classifier or
by a classifier-building algorithm. Because of this, an
indexing procedure that maps a text d
j
into a compact
representation of its content needs to be uniformly ap-
plied to the training and test documents. In fact, each
document is represented as a vector of term weights
d
i
= {w
1 j
, . . . , w
|T | j
}, where T is the set of terms
(sometimes called features) that occur at least once
in at least one document of Tr, and 0 ≤ w
k j
≤ 1 rep-
resents how much term t
k
contributes to a semantics
of document d
j
. A typical choice is to identify terms
with words, that is the bags of words assumption, and
in this case t
k
= v
k
, where v
k
is one of the words of
a vocabulary. Usually to determine the weight w
k j
of
term t
k
in a document d
j
, the standard tfidf function
is used , defined as:
t f id f (t
k
, d
j
) = N(t
k
, d
j
) · log
|Tr|
N
Tr(t
k
)
(1)
where N(t
k
, d
j
) denotes the number of times t
k
occurs
in d
j
, and N
Tr(t
k
)
denotes the document frequency of
term t
k
, i.e. the number of documents in Tr in which
t
k
occurs.
In order for the weights to fall in the [0, 1] interval
and for the documents to be represented by vectors
of equal length, the weights resulting from t f id f are
often normalized by cosine normalization, given by:
w
k j
=
t f id f (t
k
, d
j
)
q
∑
|T |
s=1
(t fid f (t
s
, d
j
))
2
(2)
Before indexing, we have performed the removal
of function words (i.e. topic-neutral words such as ar-
ticles, prepositions, conjunctions, etc.) and we have
performed the stemming procedure
1
(i.e. grouping
words that share the same morphological root).
2.2 Data Reduction
Usually, due to computational problems and to the
problem of overfitting, a dimensional reduction of the
dataset is applied. We distinguish between local and
1
Stemming has sometimes been reported to hurt effec-
tiveness, the recent tendency is to adopt it, as it reduces both
the dimensionality and the stochastic dependence between
terms.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
546

global methods, if we apply the reduction to each doc-
ument or to the whole repository respectively. An-
other distinction may be considered, that is between
the term selection and term extraction reduction tech-
niques (Sebastiani, 2002; Christopher D. Manning
and Schtze, 2009):
1. Term Selection: T
0
is a subset of T . Exam-
ples of this are methods that consider the selec-
tion of only the terms that occur in the highest
number of documents, or the selection depending
on the observation of information-theoretic func-
tions, among which we find the DIA association
factor, chi-square, NGL coefficient, information
gain, mutual information, odds ratio, relevancy
score, GSS coefficient and others.
2. Term Extraction: the terms in T
0
are not of the
same type as the terms in T (e.g. if the terms in
T are words, the terms in T
0
may not be words at
all), but are obtained by combinations or transfor-
mations of the original ones. Examples of this are
methods that consider generating, from the origi-
nal, a set of “synthetic” terms that maximize ef-
fectiveness based on term clustering, latent se-
mantic analysis, latent dirichlet allocation and
others.
In this paper we use a global method for the
term extraction based on a kind of Term Cluster-
ing technique (Sebastiani, 2002) weighted by the La-
tent Dirichlet Allocation (Blei et al., 2003) imple-
mented as the Probabilistic Topic Model (Griffiths
et al., 2007). Previous works (Berkhin, 2006; Noam
and Naftali, 2001) have confirmed the potential of su-
pervised clustering methods for term extraction.
3 PROPOSED TERM
EXTRACTION METHOD
More precisely the term extraction procedure is com-
posed of two stages and leads us to a two level repre-
sentation.
Firstly, we group terms with a high degree of
pairwise semantic relatedness so obtaining several
groups, each of them represented by a cloud of words
and their respective centroids that we call concepts
(see Fig. 1(b)). In this way we obtain the lowest level,
namely the word level. More formally, each concept
r
i
can be defined as a rooted graph of words v
s
and
a set of links weighted by ρ
is
(see Fig. 1(b)). The
weight ρ
is
can measure how far a word is related to a
concept, or in other words how much we need such a
word to specify that concept. We can consider such a
weight as a probability: ρ
is
= P(r
i
|v
s
). The probabil-
ity of the concept given a parameter µ, which we call
c
i
, is defined as the factorisation of ρ
is
P(r
i
|{v
1
, ·· · , v
V
µ
}) =
1
Z
C
∏
s∈S
µ
ρ
is
(3)
where Z
C
=
∑
C
∏
s∈S
µ
ρ
is
is a normalisation constant,
V
µ
is the number of words defining the concept, such
a number depending on the parameter µ.
After, we compute the second level, namely the
conceptual level, by inferring semantic relatedness
between centroids, and so concepts (see Fig. 1(a)).
More formally, let us define a Graph of Concepts as a
triple G
R
= hN, E, Ri where N is a finite set of nodes,
E is a set of edges weighted by ψ
i j
on N, such that
hN, Ei is an a-directed graph (see Fig. 1(a)), and R is
a finite set of concepts, such that for any node n
i
∈ N
there is one and only one concept r
i
∈ R. The weight
ψ
i j
can be considered as the degree of semantic corre-
lation between two concepts r
i
is-related
ψ
i j
-to r
j
and
it can be considered as a probability: ψ
i j
= P(r
i
, r
j
).
The probability of G
R
given a parameter ν can be
written as the joint probability between all the con-
cepts. By following the theory on the factorisation of
undirected graph, we can consider such a joint proba-
bility as a product of functions where each of this can
be considered as the weight ψ
i j
. We have
P(G
R
|ν) = P(r
1
, ·· · , r
H
|ν) =
1
Z
∏
(i, j)∈E
ν
ψ
i j
(4)
where H is the number of concepts, Z =
∑
G
R
∏
(i, j)∈E
ν
ψ
i j
is a normalisation constant and the
parameter ν can be used to modulate the number of
edges of the graph.
The resulting structure is a mixed Graph of Terms
(mGT ) composed of such two levels of information,
the conceptual level and the word level, see Fig. 2. A
mGT is defined by the probability P(G
R
|ν), which
defines a graph of connected H concepts and the num-
ber of edges depends on ν, and by H probabilities
of the concepts, P(r
i
|{v
1
, ·· · , v
V
µ
i
}), where the num-
ber of edges depends on µ
i
. Once each ψ
i j
and ρ
is
is known (Relations Learning), to determine the final
graph we need to compute the appropriate set of pa-
rameters Λ = (H, ν, µ
1
, ·· · , µ
H
) (Parameters Learn-
ing), which establishes the final shape of the graph,
that is the number of pairs and the number of both
words and concepts.
3.1 Relations Learning
We consider each concept as lexically represented by
a word, then we have that ρ
is
= P(r
i
|v
s
) = P(v
i
|v
s
)
A NOVEL SUPERVISED TEXT CLASSIFIER FROM A SMALL TRAINING SET
547
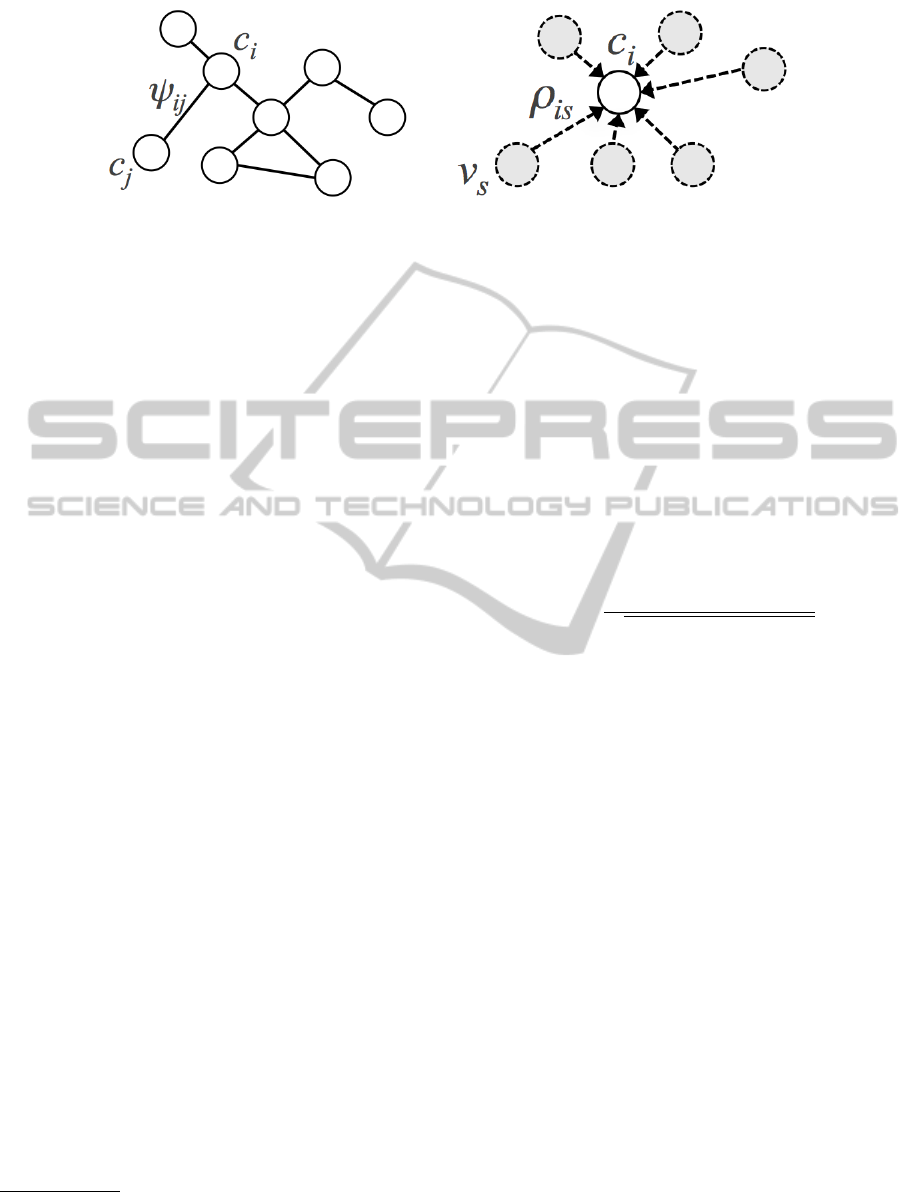
(a) (b)
Figure 1: 1(a) Theoretical representation of the conceptual level. 1(b) Graphical representation of the word level.
and ψ
i j
= P(r
i
, r
j
) = P(v
i
, v
j
). As a result , all the
relations of the mGT can be represented by P(v
i
, v
j
)
∀i, j ∈ V which can be considered as a word asso-
ciation problem and so it can be solved through a
smoothed version of the generative model introduced
in (Blei et al., 2003) called latent Dirichlet allocation,
which makes use of Gibbs sampling (Griffiths et al.,
2007)
2
.
Furthermore, it is quite important to make clear
that the mixed Graph of Terms can not be considered
as a co-occurrence matrix. In fact, the core of the
graph is the probability P(v
i
, v
j
), which we compute
through the probabilistic topic model and particularly
thanks to the word association problem, that solves
the probability P(v
i
|v
j
). In the topic model, the word
association can be considered as a problem of predic-
tion: given that a cue is presented, which new words
might occur next in that context? It means that the
model does not take into account the fact that two
words occur in the same document, but that they oc-
cur in the same document when a specific topic is as-
signed to the document itself (Griffiths et al., 2007), in
fact P(v
i
|v
j
) is the result of a sum over all the topics.
3.2 Parameters Learning
Once each ψ
i j
and ρ
is
is known, we have to find a
value for the parameter H, which establishes the num-
ber of concepts, a value for ν and finally values for µ
i
,∀i ∈ [1, ··· , H]. As a consequence, we have H + 2
parameters which modulate the shape of the graph. If
we let the parameters assuming different values, we
can observe different graph mGT
t
for each set of pa-
rameters, Λ
t
= (H, ν, µ
1
, ·· · , µ
H
)
t
extracted from the
same set of documents, where t is representative of
different parameter values.
As we have already discussed, term extraction at-
tempts to generate, from the original set T , a set
2
The authors reported the formulation that brings from
the LDA to P(v
i
, v
j
) in a paper that can not be cited due to
the blind review.
T
0
T of “synthetic” terms that maximize effective-
ness. In this case each “synthetic’ term is represented
by a pair of related words while the semantic relat-
edness between pairs, of both the conceptual and the
word level, namely ψ
i j
and ρ
is
, that we can simply
call boost of the term k, b
k
, gives a degree of rele-
vance to each pair. In practice, we have that each term
t
k
= (v
i
, v
j
), that is not the simple bags of words as-
sumption, and w
k j
being the weight calculated thanks
to the t f id f model applied to the pairs represented
through t
k
, and with the addition of the boost b
k
. For-
mally we have
w
k j
=
t f id f (t
k
, d
j
) · b
k
q
∑
|T
p
|
s=1
(t fid f (t
s
, d
j
) · b
k
)
2
(5)
Note that the boost, due to the fact that is a probability
factor, is such that 0 ≤ b
k
≤ 1. Moreover |T
p
| is the
number of pairs of the mGT , considered as composed
of all possible combinations of words of the initial
vocabulary, that has cardinality |T |.
The scope of this term extraction is to reduce the
set |T
p
| to a smaller set |T
0
p
|, such that the corre-
sponding set of words, composing the pairs belonging
to the reduced set |T
0
p
|, has dimension |T
0
| |T |.
A way of reducing the set of pairs is to change the
set of parameters Λ
t
= (H, ν, µ
1
, ·· · , µ
H
)
t
until we
have maximised the effectiveness, with the condition
that the cardinality of the set of pairs is such that
|T
0
p
| |T
p
|.
A way of saying that a mGT , given the parame-
ters, is the best possible for that set of documents is
to demonstrate that it produces the maximum score
attainable for each of the documents when the same
graph is used as a knowledge base for classify a set
containing just those documents which have fed the
mGT builder, that is the training set Tr. The re-
sult of the parameter learning procedure is an ex-
plict profile, that is the best mGT , namely the classi-
fier c
i
= {w
1i
, . . . , w
|T
0
p
|i
}, belonging to the same |T
0
p
|-
dimensional space in which documents are also rep-
resented. In this case we have a linear classifier that,
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
548
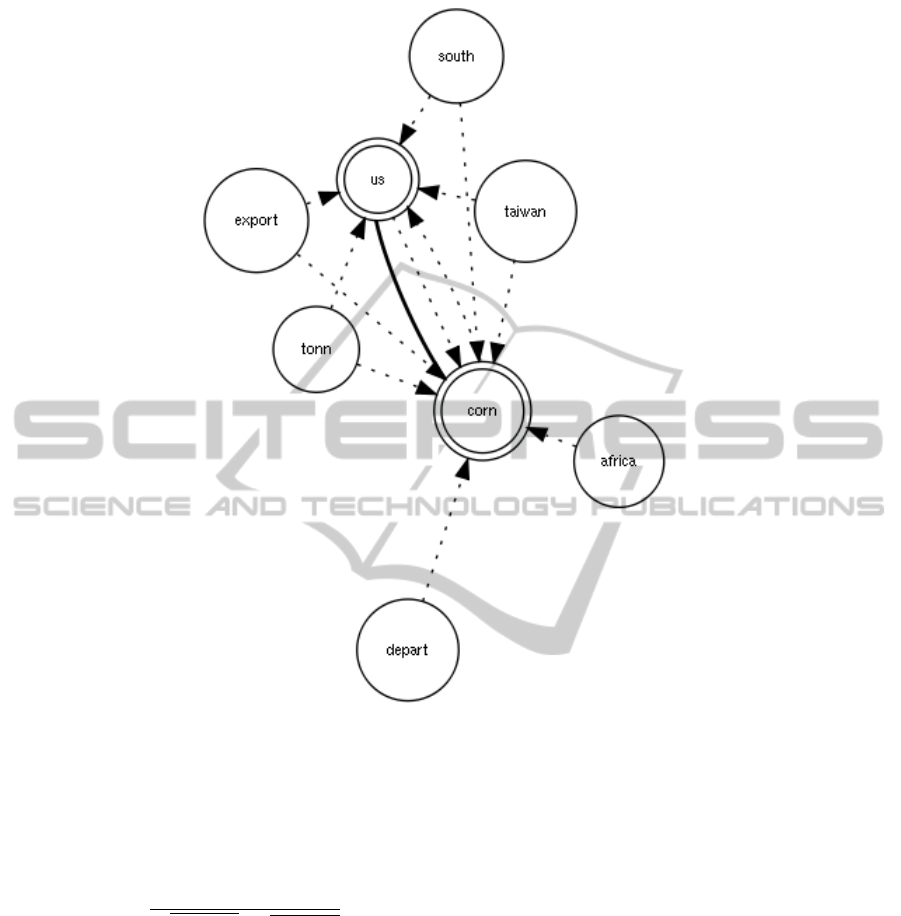
Figure 2: Part of the mGT learnt on the topic “Corn”. We have 2 concepts (double circle) and 6 words (single circle).
thanks to the Vector Space Model theory, measure the
degree of relatedness by computing (when both clas-
sifier and document weights are cosine normalized)
the cosine similarity:
S(c
i
, d
j
) =
∑
|T
0
p
|
k=1
w
ki
· w
jk
q
∑
|T
0
p
|
k=1
w
2
ki
·
q
∑
|T
0
p
|
k=1
w
2
k j
(6)
By performing a classification task that uses the
current graph mGT
t
, represented through the set of
the classifier weights, on the same repository Tr, we
obtain a score for each document d
j
and then we have
S
t
= {S(c
i
, d
1
), ·· · , S(c
i
, d
|Tr|
)}
t
, where each of them
depends on the set Λ
t
. To compute the best value of
Λ we can maximise the score value for each docu-
ments, which means that we are looking for the graph
which best describes each document of the repos-
itory from which it has been learnt. It should be
noted that such an optimisation maximises at same
time all |Tr| elements of S
t
. Alternatively, in order
to reduce the number of the objectives to being op-
timised, we can contemporary maximise the mean
value of the scores and minimise their standard de-
viation, which turns a multi-objectives problem into
a two-objectives one. Additionally, we can reformu-
late the latter problem by means a linear combina-
tion of its objectives, thus obtaining a single objec-
tive function, i.e., Fitness (F ), which depends on Λ
t
,
F (Λ
t
) = E
m
[S(q
t
, w
m
)] − σ
m
[S(q
t
, w
m
)], where E
m
is the mean value of all element of S
t
and σ
m
be-
ing the standard deviation. By summing up, the pa-
rameters learning procedure is represented as follows,
Λ
∗
= argmax
t
{F (Λ
t
)}. We will see in the next section
how we have performed the optimisation phase.
3.2.1 Optimisation Procedure
The fitness function depends on H + 2 parameters,
hence the space of possible solutions could grow ex-
ponentially. Due to the fact that we would not have
small or too big graph (we wish that |T
0
p
| |T
p
|
which is equal to say that |T
0
| |T |), we suppose
A NOVEL SUPERVISED TEXT CLASSIFIER FROM A SMALL TRAINING SET
549

that the number H of concepts can vary from a mini-
mum of 5 to a maximum of 20, and considering that
it is an integer number we conclude that the number
of possible values for H is 15. We have empirically
chosen these values for H considering that we wish to
have at most |T
0
p
| ≈ 300
3
.
ψ
i j
and ρ
is
are probabilities, and so real value, we
have that ν ∈ [0, 1] and each µ
i
∈ [0, 1]. It means that if
we use a step of 1% to explore the entire set [0, 1], then
we have 100 possible values for ν and 100 for each µ
i
,
which makes 100×100×H ×15 possible values of Λ,
that is 750, 000 for H = 5 and 3, 000, 000 for H = 20.
To limit such a space we can reduce the numbers of
parameters, for instance we can consider µ
i
= µ, ∀i ∈
[1, ·· · , H] and so obtaining 150, 000, independently of
H, possible values of Λ.
Searching for the best solution is still not easy and
it does not provide an accurate solution, because of
the big number of possible values and due to the lin-
ear exploration strategy of the set [0, 1] we are em-
ploying. In fact, by analysing how the values of ψ
i j
and ρ
is
are distributed along the set [0, 1], we note that
they are not uniformly distributed. It means that many
values of ψ
i j
and ρ
is
are likely closer than 1% with the
consequence that if the thresholds ν and µ are chosen
thanks to that linear exploration then many values will
be treated in the same way. To solve this problem one
can think to reduce the step from 1% to 0.1% and so
obtaining more accuracy in the exploration of the set
[0, 1]. The problem in this case is that the space of so-
lution can grow exponentially, and so this way is not
feasible. Another way to reduce the space can be the
application of a clustering methods, like the K-means
algorithm, to all ψ
i j
and ρ
is
values (Bishop, 2006). In
this way we can have a space of possible values ex-
tracted by a no-uniform procedure directly adapted to
the real numbers and not to the set which the numbers
belong to. Following this approach and choosing for
instance 10 classes of values for ν and µ, we obtain
that the space of possible Λ is 10 × 10 × 15, that is
1, 500. As a consequence, the optimum solution can
be exactly obtained after the exploration of the en-
tire space of solutions. This reduction allows us to
compute a mGT from a repository composed of few
documents in a reasonable time, for instance for 10
documents it takes about 30 seconds with a Mac OS
X based computer and a 2.66 GHz Intel Core i7 CPU
and a 8GB RAM. Otherwise we need an algorithm
based on a random search procedure in big solution
spaces, for instance Evolutionary Algorithms would
be suitable for this purpose, which can be very slow.
3
This number is usually employed in the case the Sup-
port Vector Machine, which have demonstrated to be one of
the best.
4 INDUCTIVE CONSTRUCTION
OF THE CLASSIFIER
The inductive construction of a ranking classifier for
category c
i
∈ C usually consists in the definition of
a function CSV
i
: D → [0, 1] that, given a document
d
j
, returns a categorization status value (CSV
i
(d
j
))
for it, i.e. a number between 0 and 1 that, repre-
sents the evidence for the fact that d
j
∈ c
i
, or in other
words it is a measure of vector closeness in |T
0
p
|-
dimensional space. Following this criterion each doc-
uments is then ranked according to its CSV
i
value, and
so the system works as a document-ranking text clas-
sifier, namely a “soft” decision based classifier. As
we have discussed in previous sections we need a bi-
nary classifier, also known as “hard” classifier, that is
capable of assign to each document a value T or F to
measure the vector closeness. A way turn a soft clas-
sifier in a hard one is to define a threshold γ
i
such that
CSV
i
(d
j
) ≥ γ
i
is interpreted as T while CSV
i
(d
j
) ≤ γ
i
is interpreted as F. We have adopted an experimen-
tal method, that is the CSV thresholding (Sebastiani,
2002), which consists in testing different values for
γ
i
on a sub set of the training set (the validation set)
and choosing the value which maximizes effective-
ness. Different γ
i
’s have been chosen for the different
c
i
’s.
Table 1: mGT for the topic Corn. (see Fig. 2).
Conceptual Level
Concept i Concept j Relation Factor (ψ
i j
)
corn us 4,0
··· ··· ···
Word Level
Concept i Word s Relation Factor (ρ
is
)
corn south 2.0
corn us 1.96
corn export 1.69
corn africa 1.0
··· ··· ···
us south 1.17
us taiwan 1.0
··· ··· ···
5 EVALUATION
We have considered a classic text classification prob-
lem performed on the Reuters-21578 repository. This
is a collection of 21,578 newswire articles, originally
collected and labeled by Carnegie Group, Inc. and
Reuters, Ltd.. The articles are assigned classes from
a set of 118 topic categories. A document may be
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
550

Table 2: Distribution of the ModApte split (columns “train”
and “test”). Distribution of the training set employed by the
proposed method (“mGTtrain” column).
class mGTtrain train test
earn 29 2877 1087
acq 17 1650 719
money-fx 6 538 179
grain 5 433 149
crude 4 389 189
trade 4 369 119
interest 4 347 131
ship 2 197 89
wheat 3 212 71
corn 2 182 56
total 76 7194 2249
assigned several classes or none, but the common-
est case is single assignment (documents with at least
one class received an average of 1.24 classes). For
this task we have used the ModApte split which in-
cludes only documents that were viewed and assessed
by a human indexer, and comprises 9,603 training
documents and 3,299 test documents. The distribu-
tion of documents in classes is very uneven and we
have evaluated the system on only documents in the
10 largest classes, in table 2 the distribution of the ten
largest classes is reported (Christopher D. Manning
and Schtze, 2009)
4
.
As discussed before we have considered the any-
of problem and so we have learnt 10 two-class clas-
sifiers, one for each class, where the two-class clas-
sifier for class c is the classifier for the two classes c
and its complement c. For each of these classifiers,
we have measured recall, precision, and accuracy, but
we have focused on measures of accuracy named F
1
measure, and on a single aggregate measure that com-
bines the measures for individual classifiers, that is
the Macroaveraging, which computes a simple aver-
age over classes, and the Microaveraging pools per-
document decisions across classes (Sebastiani, 2002;
Christopher D. Manning and Schtze, 2009).
Note that the mGT is different from a simple list
of key words because of the presence of two features:
the relations between terms and the hierarchical dif-
ferentiation between simple words and concepts. To
demonstrate the discriminative property of such fea-
tures we have to prove that the results obtained per-
forming the proposed approach are significantly bet-
ter than the results obtained by performing the same
queries composed of the simple list of words extracted
from the mGT . As a result, the aim of the evaluation
4
Note that considering the 10 largest classes means 75%
of the training set and 68% of the test set.
phase is twofold:
1. To demonstrate the discriminative property of the
mGT compared with a method based on only the
words from the mGT without relations (named
Words List W L);
2. To demonstrate that the mGT achieves good per-
formance when 1% of the training set is employed
for each class. Here comparison with well known
methods trained on the whole training set will be
reported.
We have randomly selected the 1% from each
training set (in table 2 is reported the comparison with
the original training set dimension) and moreover we
have performed the selection 100 times in order to
make the results independent of the particular docu-
ments selection. As a result we have 100 repositories
and from each of them we have calculated 100 mGT s
by performing the parameters learning described de-
scribed above. Due to the fact that each optimisation
procedure brings to a different graph (from a topo-
logical point of view), we have a different number of
pairs for each of them. We have calculated the av-
erage number of pairs for each topic and the corre-
sponding average number of terms, see table 3. Note
that the average size of |T
0
p
| is 120, while the aver-
age size of |T
0
| is 33 (150 and 47 respectively in the
case of the best performance). The overall number
of features observed by our method is, independently
of the topic, less than the number considered in the
case of Rocchio and Support Vector Machines, in fact
they have employed a term selection process obtain-
ing |T
0
| equals to 50 and 300 respectively.
In table 4 we have reported the best accuracy (cal-
culate in the F
1
measure) obtained by our method
and the average value obtained by all 100 graphs. It
is surprising how the proposed method, even if the
training set is smaller than the original ones, is ca-
pable of clustering in most of the case with an accu-
racy comparable to that obtained by well-known ap-
proaches (amongst which we find the worst case that
is Rocchio and best that is Support Vector Machines)
(Christopher D. Manning and Schtze, 2009). Note
that the performance of the proposed method is, inde-
pendently of the topic, better than the W L, so demon-
strating that the graph representation possesses better
discriminative properties than a simple list of words.
Furthermore it is surprising how mGT performs in
the same way of SVM in the case of the topic acq and
comparable to Rocchio and Naive Bayes for the other
topics. Finally, it should be noticed that the good per-
formances shown by W L are motived by the fact that
the list of words is formed by the terms extracted form
the mGT .
A NOVEL SUPERVISED TEXT CLASSIFIER FROM A SMALL TRAINING SET
551

Table 3: Average number of pairs and words for each topic. Values for each run and for each the best run.
Topic Av. #pairs Av. #words #pairs@max #words@max
earn 83 43 17 17
acq 75 38 162 87
money-fx 98 33 357 48
grain 127 36 204 64
crude 153 40 262 50
trade 178 48 229 80
interest 105 28 143 83
ship 113 16 54 15
wheat 124 26 18 15
corn 139 20 50 15
Average 120 33 150 47
Table 4: F
1
and micro-avg measure for NB, Rocchio and SVM when 100% of the training set is employed (Christopher
D. Manning and Schtze, 2009). The same measures and the macro-avg for the mGT and W L.
NB
(100%)
Rocchio
(100%)
SVM
(100%)
max
W L
(1%)
av.
W L
(1%)
max
mGT
(1%)
av.
mGT
(1%)
earn 96 93 98 82 69 92 83
acq 88 65 94 73 60 94 74
money-fx 57 47 75 39 30 48 35
grain 79 68 95 64 45 68 47
crude 80 70 89 60 40 71 49
trade 64 65 76 53 39 61 46
interest 65 63 78 48 34 50 45
ship 85 49 86 71 30 73 44
wheat 70 69 92 82 41 86 54
corn 65 48 90 54 30 57 47
micro-avg
(top 10)
82 65 92 70 − 80 −
macro-avg
(top 10)
− − − 66 − 70 −
6 CONCLUSIONS
In this work we have demonstrated that a term ex-
traction procedure based on a mixed Graph of Terms
representation is capable of achieving better perfor-
mance than a method based on a simple term selection
obtained considering only the words composing the
graph. Moreover we have demonstrated that the over-
all performance of the method is good even if 1% of
the training set has been employed. As a future work
we consider to measure performances of well known
methods when trained on the same, small, percentage
of the training set. Furthermore, we are interested in
finding an analytic method to set the suitable thresh-
old to the CSV’s.
REFERENCES
Berkhin, P. (2006). A survey of clustering data mining tech-
niques. In Kogan, J., Nicholas, C., and Teboulle, M.,
editors, Grouping Multidimensional Data, pages 25–
71. Springer Berlin Heidelberg.
Bishop, C. M. (2006). Pattern Recognition and Machine
Learning. Springer.
Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). Latent
dirichlet allocation. Journal of Machine Learning Re-
search, 3(993–1022).
Christopher D. Manning, P. R. and Schtze, H. (2009). In-
troduction to Information Retrieval. Cambridge Uni-
versity.
Griffiths, T. L., Steyvers, M., and Tenenbaum, J. B. (2007).
Topics in semantic representation. Psychological Re-
view, 114(2):211–244.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
552

Ko, Y. and Seo, J. (2009). Text classification from unlabeled
documents with bootstrapping and feature projection
techniques. Inf. Process. Manage., 45:70–83.
Lewis, D. D., Yang, Y., Rose, T. G., and Li, F. (2004). Rcv1:
A new benchmark collection for text categorization
research. J. Mach. Learn. Res., 5:361–397.
McCallum, A., Nigam, K., Rennie, J., and Seymore, K.
(1999). A machine learning approach to building
domain-specific search engines. In Proceedings of
the 16th international joint conference on Artificial in-
telligence - Volume 2, pages 662–667. Morgan Kauf-
mann.
Noam, S. and Naftali, T. (2001). The power of word clus-
ters for text classification. In In 23rd European Collo-
quium on Information Retrieval Research.
Sebastiani, F. (2002). Machine learning in automated text
categorization. ACM Comput. Surv., 34:1–47.
A NOVEL SUPERVISED TEXT CLASSIFIER FROM A SMALL TRAINING SET
553
