
THE MULTIDIMENSIONAL 0-1 KNAPSACK PROBLEM
A New Heuristic Algorithm Combined with 0-1 Linear Programming
Anikó Csébfalvi and György Csébfalvi
University of Pécs, Pécs, Hungary
Keywords: Multidimensional 0-1 knapsack problem, Heuristic algorithm, 0-1 Linear programming problem.
Abstract: In this paper, we present a new population-based heuristic for the multidimensional 0-1 knapsack problem
(MKP) which is combined with 0-1 linear programming to improve the quality of the final heuristic
solution. The MKP is one of the most well known NP-hard problems and has received wide attention from
the operational research community during the last four decades. MKP arises in several practical problems
such as the capital budgeting problem, cargo loading, cutting stock problem, and computing processors
allocation in huge distributed systems. Several different techniques have been proposed to solve this
problem. However, according to its NP-hard nature, exact methods are unable to find optimal solutions for
larger problem instances. Heuristic methods have become the alternative, and the last generation of them,
are being successfully applied to this problem. Hence, in practice, heuristic algorithms to generate near-
optimal solutions for larger problem instances are of special interest. The presented hybrid heuristic
approach exploits the fact, that using a state-of-the-art solver a small binary linear programming (BLP)
problem can be solved within reasonable time. The computational experiments show that the presented
combined approach produces highly competitive results in significantly shorter run-times than the
previously described approaches.
1 INTRODUCTION
The multidimensional 0-1 knapsack problem (MKP)
is one of the most well known NP-hard problems
and has received wide attention from the operational
research community during the last four decades.
MKP arises in several practical problems such as the
capital budgeting problem, cargo loading, cutting
stock problem, and computing processors allocation
in huge distributed systems. Several different
techniques have been proposed to solve this
problem. However, according its NP-hard nature,
exact methods are unable to find optimal solutions
for larger problem instances. Heuristic methods have
become the alternative, and the last generation of
them, are being successfully applied to this problem.
Hence, in practice, heuristic algorithms to generate
near-optimal solutions for larger problem instances
are of special interest.
The multidimensional 0-1 knapsack problem
(MKP) can be defined as
max
N
j
jj
XPF
1
(1)
MiCXW
ij
N
i
ij
,,, 1
1
(2)
NjX
j
,,,, 110
(3)
where N is the number of items,
M
is the number
of constraints,
0
j
P
,
Nj ,,, 21
is the profit
of item
j , 0
ij
W ,
Mi ,,, 21
are the weights
of item
j , and 0
i
C ,
Mi ,,, 21 are the
capacities of the knapsack.
In this paper, we present a new heuristic for
MKP combined with BLP to improve the quality of
the final heuristic solution. The remaining of this
paper is organized as follows. In Section 2 and 3 we
describe our new hybrid heuristic algorithm (HH)
and the BLP model developed to improve the quality
of the final heuristic solution. In Section 4 we
present detailed computational results to verify the
new conception presented in Section 2 and 3.
Finally, Section 5 draws conclusions from this study.
203
Csébfalvi A. and Csébfalvi G..
THE MULTIDIMENSIONAL 0-1 KNAPSACK PROBLEM - A New Heuristic Algorithm Combined with 0-1 Linear Programming.
DOI: 10.5220/0003671302030207
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 203-207
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
2 HEURISTIC ALGORITHM
According to the systematic simplifications our
population-based heuristic algorithm uses only two
operators (random selection and perturbation) and
starts with a "more or less random" initial
population, where it means that the starting
population is given by random perturbation of the
relaxed solution:
NjXX
jj
,,,,,
~~
I
~
21 1 0
(4)
where the relaxation of MKP is defined as follows:
max
~
N
j
jj
XPP
1
(5)
MiWXW
ij
N
i
ij
,,,
~
1
1
(6)
NjX
j
,,,,
~
1 1 0
(7)
Perturbation is a crucial point of our algorithm,
because we have to balance between the diversity
and intensity. In our approach, we used a simple but
effective trick to resolve this problem. When a
relaxed variable value is one (zero) then we replace
it with a random value next to one (zero) from a
truncated gauss distribution with mean one (zero).
Otherwise, we replace the relaxed variable value
with a randomly generated truncated gauss
distribution value, which is spreading around the
relaxed value. Naturally, the quality of the starting
population is highly affected by the spreading range.
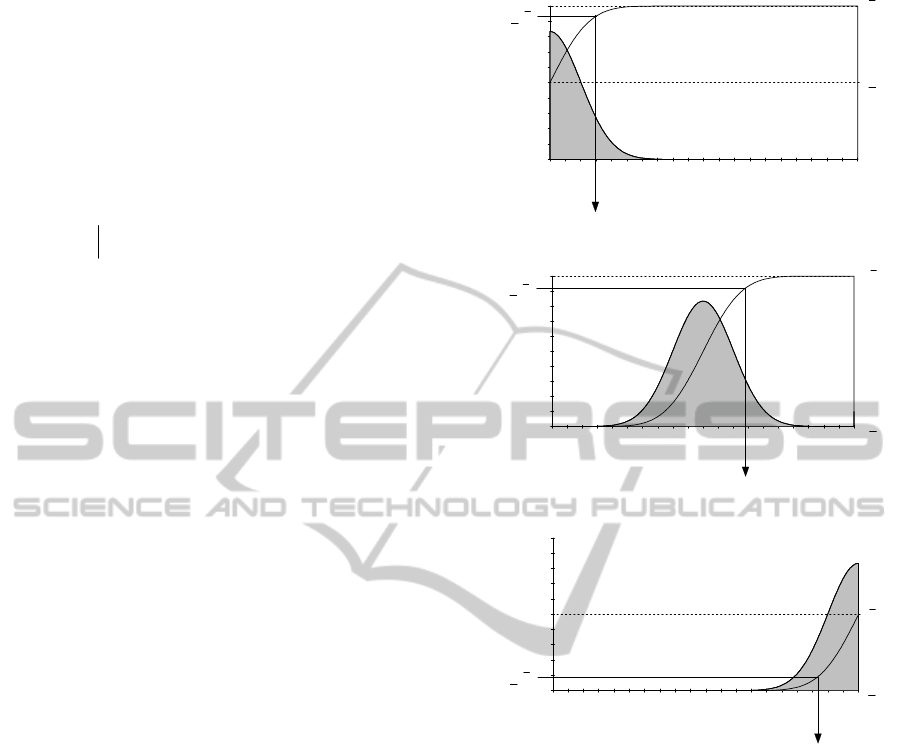
The essence of the initial population generation is
shown in Figure 1-3.
The two most important parameters of our hybrid
heuristic algorithm are the population size
S and
the number of generations
G . A solution in the
current generation
g
, where
Gg ,,, 21 is
represented by the following triplet:
sss
P,X,I
~
,
Ss ,,, 21
(8)
where vector
s
I
~
is the description of the importance
of the different items,
s
X
is the vector of the binary
indicators, and
s
P
is the profit value in the
corresponding feasible solution given by a usual
primary greedy heuristic without “pseudo-utility”
computation. The heuristic begins with an empty
solution and adds items to the solution in the given
importance order without violating constraints.
1
0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.
pp,Uniform
p
p
0
j
I
~
Figure 1: Random perturbation with zero relaxed value.
1
0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.
pp ,Uniform
p
p
10
j
I
~
Figure 2: Random perturbation with fractional value.
1
0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.
pp,Uniform
p
p
1
j
I
~
Figure 3: Random perturbation with one relaxed value.
As we mentioned the first generation is
generated from the relaxed solution by random
perturbation, after that, in each generation we select
S "more or less good" solution using the random
selection operator and perturbate it using the
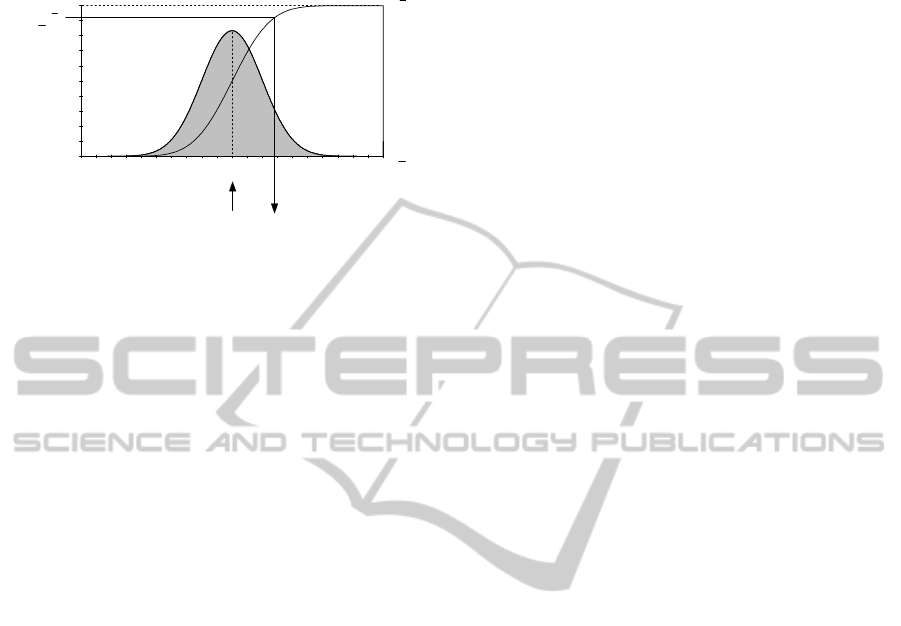
perturbation operator shown in Figure 4. The higher
the profit value, the higher the chance that a solution
will be selected by the selection operator. When the
perturbated solution is better than the worst solution
in the current population, the worst will be replaced
by the better one. In the algorithm the diversity is
decreasing systematically generation to generation
characterized by an exponentially decreasing
standard deviation function
g
,
Gg ,,, 21 ,
which can be described by a tunable parameter pair:
G
,
1
. The higher the standard deviation, the
higher the variability (diversity) of the searching
process is. The quality of the searching process is
highly affected by the value of these parameters. In
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
204
other words, these are the “golden numbers” of the
algorithm.
1
0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.
pp ,Uniform
p
p
new
~
j
I
old
~
j
I
Figure 4: Random perturbation.
The algorithm maintains the dynamically
changing
bestbest
P X,
set.
3 BLP MODEL
At the termination of the heuristic algorithm,
solution
bestbest
P X,
may be improved at
reasonable additional CPU time by solving a set of
randomly generated small BLP problems.
The idea is a natural extension of the well-known
"last added items" heuristics (for example: (Loulou,
Michaelides, 1979); (Volgenant and Zwiers, 2007),
and (Fleszar and Hindi, 2009)), which exploits the
fact, that using a state-of-the-art solver, a small BLP
problem can be solved very quickly.
The essence of the new approach is very simple:
we select randomly
K
items from the knapsack and
K
items from the complementary set. After that we
solve the knapsack problem to optimality for the
selected subset, and update the best solution if the
new arrangement is better than the old one. We
repeat these steps
C times.
Naturally, the time requirement and the
efficiency of the improvement is a function of
C
and
K
. The larger the selected subset size, the
higher the chance of success but higher the
computational cost according to the NP-hard nature
of the BLP subproblems.
4 COMPUTATIONAL RESULTS
The algorithm of the proposed model has been
programmed in Compaq Visual Fortran
6.5. To
solve the BLP problems the callable version of
Cplex 12.2 was used. Naturally, this solver can be
replaced by any other commercial (academic) solver.
The computational results were obtained by running
the algorithm on a 1.8 GHz Pentium IV IBM PC
with 256 MB of memory under Microsoft Windows
XP
operation system.
Standard “large-sized” test data available from
OR-Library were used to test the algorithm. These
data contain randomly generated 0-1 MKPs with
different numbers of constraints, variables, and
tightness ratios:
750 50 250
500 250 100
30 10 5
.,.,.α
,,N
,,M
(9)
There are 10 problem instances for each
combination giving 270 test cases in total. The
algorithm was run once for each problem instance.
Since the optimal solution values for most of these
problems are not known, the quality of a solution
was measured by the percentage gap of the solution
value with respect to the optimal value of the LP-
relaxation of the MKP.
According to our preliminary investigations, we
have run our algorithm with the following global
parameter values, where the bold numbers mean
MKP specific “golden numbers”:
S
{10, 100, 1000}
G
10
1
0.1
G
0.01
K
25
C
10
We compared our hybrid heuristic HH with the
following heuristics of the literature (see: Table 1-2):
AGNES (Freville and Plateau , 1994);
ADP (Bertsimas and Demir, 2002);
SMA (Hanafi et al., 1996);
HDP (Boyer et al., 2008);
HDP+LPC (Boyer et al., 2008)
ILPH (Hanafi and Wilbaut, 2011)
Numerical results show that HH is a fast algorithm
that is competitive with the currently best ILPH,
HDP and HDP+LPC algorithms for MKP for
instance sets MKNAPCB 1-9 (OR-Library).
In the case of ILPH the authors investigated only
the 90 largest (hardest) instances with
.
500N We
have to mention, that in Table 1 we compared the
ILPH results with the relaxed solutions. In (Hanafi
and Wilbaut, 2011) the authors compared the ILPH
results with the currently best solutions of the
literature, which is a dynamically changing measure
THE MULTIDIMENSIONAL 0-1 KNAPSACK PROBLEM - A New Heuristic Algorithm Combined with 0-1 Linear
Programming
205

Table 1: Average gap (%).
Average gap (%)
Set N M
HH HH HH HDP
HDP SMA ADP AGNES ILPH
+
100 1000 10000 LPC
1 100 5 0.95 0.8 0.72 0.57 0.69 2.68 1.72 0.88
2 250 5 0.34 0.29 0.23 0.16 0.22 1.17 0.58 0.29
3
500 5
0.21 0.14 0.10 0.07 0.08 0.59 0.26 0.12 0.05
4 100 10 1.45 1.27 1.16 0.95 1.22 3.60 1.97 1.54
5 250 10 0.59 0.49 0.44 0.32 0.46 1.60 0.76 0.57
6
500 10
0.32 0.25 0.21 0.16 0.21 0.80 0.38 0.26 0.11
7 100 30 2.28 1.96 1.87 1.81 2.04 5.13 2.70 3.22
8 250 30 1.04 0.89 0.79 0.77 0.89 2.60 1.18 1.41
9
500 30
0.63 0.51 0.45 0.42 0.48 1.45 0.58 0.72 0.31
0.87 0.73 0.66 0.58 0.70 2.18 1.13 1.00
Table 2: Average processing time (sec).
Average processing time (sec)
Set N M
HH HH HH HDP
HDP SMA ADP AGNES ILPH
+
100 1000 10000 LPC
1 100 5 0.09 0.30 3.18 0.60 0.03 0.03
2 250 5 0.14 0.60 6.43 1.00 0.10 0.57 0.07
3
500 5
0.24 1.45 14.85 1.13 0.53 4.57 0.30 0.10 46.27
4 100 10 0.10 0.24 3.20 1.00 0.03 0.03 0.03
5 250 10 0.15 0.63 6.69 0.97 0.17 0.70 0.10 0.03
6
500 10
0.26 1.50 15.85 4.03 0.83 5.70 0.43 0.13 278.03
7 100 30 0.11 0.26 3.33 3.97 1.67 0.10 0.07 0.03
8 250 30 0.17 0.66 7.39 21.20 9.87 1.40 0.37 0.10
9
500 30
0.25 1.79 18.08 93.37 26.4 11.90 1.20 0.30
0.17 0.83 8.78 14.14 4.95 2.78 0.29 0.12 1928.50
of performance and therefore maybe confusing
sometimes.
According to our preliminary investigation, the
HH algorithm is not so sensitive to the “fine
tuning” of the standard deviation parameters. In
other words, these parameters can be kept “frozen”
in the algorithm independently from the problem
parameters:
NM , , which results in a practically
“tuning-free” core algorithm. Naturally
1
is more
important than
G
. When
1
extremely small, than
the searching process is unable to leave the relaxed
solution, when it is extremely large then the
algorithm forgets the relaxed solution and
practically it is working as a "brutal-force-search"
in the starting population uploading phase.
5 CONCLUSIONS
In this paper, we presented a new heuristic for
MKP combined with 0-1 linear programming to
improve the quality of the final heuristic solution.
The presented hybrid heuristic approach exploits
the fact, that using a fast state-of-the-art solver a
small BLP problem can be solved within
reasonable time.
The computational experiments show that the
presented hybrid heuristic produces highly
competitive results in significantly shorter run-
times than the previously described approaches.
An open and challenging question is that what
would be the "best" selected/unselected subset
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
206

selection strategy in the local BLP problems.
Another interesting question would be to
investigate the relation between the BLP size and
the solution quality (time) in the function of the
problem parameters:
NM , .
These questions are under investigation and the
answers will be presented in a forthcoming paper.
REFERENCES
Bertsimas, D., Demir, R., 2002. An approximate
dynamic-programming approach to multi-
dimensional knapsack problem, Management
Science, 4, 550–565.
Boyer, V., Elkihel, M., El Baz, D., 2008. Heuristics for
the 0–1 multidimensional knapsack problem,
European Journal of Operational Research, doi:
10.1016/j.ejor.2007.06.068
Mahdavi, M., Fesanghary, M., Damangir, E., 2006. An
improved harmony search algorithm for solving
optimization problems, Applied Mathematics and
Computation, doi: 10.1016 / j.amc.2006.11.033.
Fleszar, K., Hindi, K. S., 2009. Fast, effective heuristics
for the 0-1 multi-dimensional knapsack problem,
Computers & Operations Research, 36, 1602-1607.
Freville, A., Plateau, G., 1994. An efficient
preprocessing procedure for the multidimensional 0–
1 knapsack problem, Discrete Applied Mathematics,
49, 189–212.
Hanafi, S., Freville, A., El Abdellaoui, A., 1996.
Comparison of heuristics for the 0–1
multidimensional knapsack problem, Meta-
Heuristics: Theory and Application, Kluwer
Academic, 446–465.
Hanafi, S., Wilbaut, C., 2011. Improved convergent
heuristics for the 0-1 multidimensional knapsack
problem, Annals of Operations Research, 183 (1),
125-142.
Loulou, R., Michaelides, E., 1979. New greedy-like
heuristics for the multidimensional 0-1 knapsack
problem, Operations Research, 27(6), 1101-1114.
Volgenant, A, Zwiers, I.Y., 2007. Partial enumeration in
heuristics for some combinatorial optimization
problems. Journal of the Operational Research
Society, 58(1), 73-9.
THE MULTIDIMENSIONAL 0-1 KNAPSACK PROBLEM - A New Heuristic Algorithm Combined with 0-1 Linear
Programming
207
