RETROVIRAL GENETIC ALGORITHMS

Implementation with Tags and Validation Against Benchmark Functions

Alexander V. Spirov

1, 2

and David M. Holloway

Laboratory of Evolutionary Modelling, The Sechenov Institute of Evolutionary Physiology and Biochemistry

of the Russian Academy of Sciences, Saint-Petersburg, Russia

Computer Science and CEWIT, State University of New York at Stony Brook

500 Stony Brook Road, Stony Brook, NY, U.S.A.

Mathematics Department, British Columbia Institute of Technology, Burnaby, B.C., Canada

Keywords: Genetic algorithms, Recombination, Building blocks, Natural computing, Retroviral recombination.

Abstract: Classical understandings of biological evolution inspired creation of the entire order of Evolutionary

Computation (EC) heuristic optimization techniques. In turn, the development of EC has shown how living

organisms use biomolecular implementations of these techniques to solve particular problems in survival

and adaptation. An example of such a natural Genetic Algorithm (GA) is the way in which a higher

organism’s adaptive immune system selects antibodies and competes against its complement, the

development of antigen variability by pathogenic organisms. In our approach, we use operators that

implement the reproduction and diversification of genetic material in a manner inspired by retroviral

reproduction and a genetic-engineering technique known as DNA shuffling. We call this approach

Retroviral Genetic Algorithms, or retroGA (Spirov and Holloway, 2010). Here, we extend retroGA to

include: (1) the utilization of tags in strings; (2) the capability of the Reproduction-Crossover operator to

read these tags and interpret them as instructions; and (3), as a consequence, to use more than one

reproductive strategy. We validated the efficacy of the extended retroGA technique with benchmark tests on

concatenated trap functions and compared these with Royal Road and Royal Staircase functions.

1 INTRODUCTION

Classical understandings of biological evolution

served to inspire an entire order of heuristic

optimization techniques, known generally as

Evolutionary Computations (EC). Recent studies at

the molecular biology and genetic level have

conclusively shown that living organisms utilize

biomolecular implementations of EC for solution of

problems in survival and adaptation – for example

the selection of antibodies in a higher organism’s

adaptive immune system (Lewin, 2003) due to

competition with the development of antigen

variability in pathogenic organisms such as viruses

(Donelson, 1995); (Barbour and Restrepo, 2000).

The computational approach we present here is

inspired by the biology of retroviral reproduction, in

which genetic material is diversified through the

alternate use of DNA and RNA (Negroni and Buc,

2001; Galetto and Negroni, 2005). A virus entering a

host cell contains two or more copies of its genome

in RNA form. As part of the infection cycle, a single

DNA molecule is synthesized from the viral RNAs.

During the replication process the viral genome goes

through a series of intermediate states. Replication is

conducted by the retroviral reverse transcriptase

enzyme, which can be directed by signal elements

on the original RNA strands. Passing over these

elements during replica synthesis causes the

transcriptase to release the current template strand

and shift to a different one. These jumps (template

switches, strand transfers) are key events in

retroviral recombination (and will frequently lead to

a mutation in the replica, due to the insertion of an

extra nucleotide). The elements triggering template

switches are varied: breaks in the RNA molecule;

pause sites (RNA sequences that slow down replica

synthesis); or the local physical structure of the

RNA (e.g. a hairpin).

Computationally, the switch elements are

analogous to marks or tags on a string. Molecular

machines read these tags and interpret them as

instructions for further string operations. We use

233

V. Spirov A. and M. Holloway D..

RETROVIRAL GENETIC ALGORITHMS - Implementation with Tags and Validation Against Benchmark Functions.

DOI: 10.5220/0003674102330238

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 233-238

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

operators for reproduction following retroviral rules,

which we term Retroviral Genetic Algorithms or

retroGA (Spirov and Holloway, 2010). In the present

work, we extend retroGA to include: (1) the

utilization of tags in strings; (2) the capability of the

Reproduction-Crossover operator to read these tags

and interpret them as instructions; and (3), as a

consequence, for reproduction to use more than a

single strategy. It is commonly accepted that typical

combinatorial optimizations and biological evolution

fitness functions may be represented by rugged

landscapes. We use concatenated trap functions and

Royal Road (RR) functions to test the efficacy of the

extended retroGA approach on such landscapes.

2 THE retroGA APPROACH,

WITH TAGS

The initial implementation of retroGA (Spirov and

Holloway, 2010) included a Reproduction-Crossover

(RC) operator for the processes of retroviral

recombination. Here, we extend the RC operator by

introducing two different sets of tags that it may

operate on. This allows us to implement template

switching via signals in recombining sequences. In

addition, during rearrangement tags may be

changed, added, copied and/or moved (to another

site on the same string or to another string

altogether). This allows both the resultant string and

the processing scheme itself to change over

successive cycles of genetic rearrangement. This

enables the retroGA operators to use more than one

strategy for the recombination of parental sequences.

The RC operator: generates a child string from a

given parent pair, combining the functions of

reproduction and crossover (see Spirov and

Holloway, 2010). A pair of parents is selected, as in

standard GA, by one of several predetermined

strategies: truncation, roulette-wheel, etc. One string

is selected as a donor (tag γ), and the other is the

acceptor (tag Γ). This is analogous to retroviral

replication, with the RC operator corresponding to

reverse transcriptase and the parent strings to the

pair of retroviral RNA molecules. Like retroviruses,

replicating strings are circular (the N+1th element is

the 0th).

When the RC operator’s string reading and

copying procedure encounters a tag between the (i-

1)-th and i-th elements, it is interpreted, depending

on the nature of the tag, as one of the following

commands (tags are not copied unless explicitly

commanded, and no more than one tag is allowed

between regular string elements):

1. Finish the current child string and begin a new

one.

2. Finish the child string and terminate

reproduction.

3. Move tag one position to the right.

4. Switch template to the other parent string.

5. Replace the i-th element of the current parent or

child string with a copy of the j-th element of the

other parent string.

6. Mutate the j-th element of the donor, acceptor or

child string.

7. Insert an arbitrary element into the i-th position

of the current string.

8. Delete the j-th element from the current string.

9. Insert tag X into the j-th position of the donor,

acceptor, or child string.

More complex commands can be constructed from

these nine elementary instructions. Elementary

commands (5-9) have arguments.

Two different reproduction strategies are used: a)

replace a predetermined fraction of the population

by progeny; b) permit the operator to leave offspring

in the population if and only if their scores are

higher than their parents’.

Three-tag Model: Three tags and their respective

instructions (Table 1) are sufficient to implement

retroviral recombination in an evolutionary search

program. Processing of a pair of parent strings

begins with the insertion of replication cycle control

tags (Γ and γ). The basic operation is the generation

of a child (or replica) string, reading from left to

right, from the 0th to the Nth element, from one or

two alternating parent strings. The Γ and γ tags

model the role of viral RNA flanking regions in

controlling replication. Tag Λ is randomly inserted

into a certain fraction of the strings in the initial

population. It is composed of three elementary

instructions which together act as the entire

mechanism of retroviral recombination. The Λ tag

itself is analogous to a “stop-signal” on a retroviral

RNA molecule, in that it facilitates change of the

current template.

Table 1: The three tags and their definitions.

Tag Command

Γ Finish the current child string and begin a new

one.

γ Finish the child string and terminate reproduction.

Λ Insert random element into the i-th position of the

current parent string, delete element from the (i-

1)-th position of the current parent string, and

switch template.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

234

1:11111111...11000000

:00000000...000000000

:11111111...11111111

child

donor

acceptor









2:11111111...1000000

:00000000...000000000

:11111111...1111111

child

donor

acceptor









Figure 1: The first two recombination / replication cycles

in the 3-tag model. * indicates an arbitrary element of the

string.

Using the three tags, the RC operator creates a

complex (not ‘point’) mutation in each cycle,

inserting a random element to the right of a Λ tag,

deleting an element to the left of a Λ tag. After N

replication cycles, one Λ tag will change all N

elements of the string (see Figure 1 a, b). Without Λ

tags, the operator processes strings as in standard

GA (only point mutation and/or crossover

operators); with Λ tags, strings are processed with a

local search (C.f. the RHMC algorithm, Forrest and

Mitchell, 1993).

Eight-tag Model: Modification and broadening of

the list of tags and their corresponding commands

substantially increases the complexity of the

operator’s behaviour. We introduce an eight tag

model (Table 2) which captures the processes of

transposition (i.e. the behaviour of transposons, or

mobile genetic elements, see Spirov et al., 2009).

Tags Λ and λ are the only ones inserted randomly

into strings of the initial population. Unlike the 3-tag

model, tag Γ is now placed after the 0th element of

the acceptor string, and tag γ after the 0th element of

the donor string (Cf. Tables 1 and 2). With the

increased number of tags and commands, conflicts

may occur during tag interpretation. Specifically, a

command to move or copy a given tag X to a

position between elements (i-1) and i may result in a

collision with an already-present tag. To resolve

these conflicts, two new rules are introduced: how to

interpret an attempt to replace tag Λ with tag φ

(φ→Λ) or to replace tag φ with tag Λ (Λ→φ) (see

Table 2).

If the donor contains tag Λ in the position

between (i-1) and i, and the acceptor contains tag λ

in the position between (j-1) and j, then the region

between the i-th and j-th elements (inclusive) of the

acceptor after M recombination/replication cycles

(M = j – i) assumes the configuration

*Φ*Φ*Φ…*Φ*Φ*λ (* is an arbitrary element of the

string; see Fig. 2). Beginning with cycle M+1 the

RC operator produces progeny with random

sequences in this index range. The configuration of

this region in the child strings becomes

τ*φ*φ*φ…*φ*φ*Τ

. With this chance combination

of tags, this region of the child string can function

independently from the rest of the string.

Table 2: The eight tags and their definitions.

Tag Command

γ Finish the child string and terminate reproduction.

Γ Finish the child string and begin a new one.

λ Switch template, mutate the i-th element of the

current string, insert tag Φ into the (i+1)-th position

of the current string and insert tag τ into the child

string.

Λ Switch template and insert tag T into the child string.

φ Mutate element after the tag, copy the tag one step to

the right, insert tag φ into the same position on the

child string.

Φ Copy this tag onto the paired string.

φ→Λ Transpose tag Λ one step to the right, insert tag φ in

this position, and change the i-th element of the

current string to the i-th element of the paired string.

Λ→φ Cancel replacement, but switch template.

T Switch template.

τ Copy this tag onto the paired string.

Because of this property, a situation may arise in

a later generation where the donor string carries the

τ*φ*φ*φ…*φ*φ*Τ fragment, and the acceptor

string does not. In this case, the fragment gets copied

to the second parent (acceptor) string during a

reproductive cycle, due to combined action of tags τ,

φ, Τ (see Table 2).

If the arbitrary sequence between tags τ and Τ

forms a functional sequence (or BB, see below),

copying the fragment can be evolutionarily

favourable. By transposing itself, this fragment can

disseminate throughout the population (C.f. Spirov

et al., 2009).

GRC Operator: The fact that some retroviral

recombinatorial events can have more than two

parental sequences inspired us to generalize the RC

operator (GRC operator) to N parental strings for

each child sequence (Spirov and Holloway, 2009).

However, the GRC operator does not currently

process tags; this is one of our future directions.

Figure 2: The formation of a local mutagenesis mechanism

between tags Λ and λ. a) earlier; b) later.

RETROVIRAL GENETIC ALGORITHMS - Implementation with Tags and Validation Against Benchmark Functions

235

3 RESULTS AND DISCUSSION

Fitness Functions to Study Hard Evolutionary

Problems: There is every reason to believe that both

biological evolution and natural GA solve problems

of considerable difficulty. The current literature

provides grades and classifications for problem

difficulty; we select several representative types of

problem with which to benchmark our approach.

Typical combinatorial optimization or biological

evolution fitness functions may be described by

rugged landscapes (Kauffman and Levin, 1987),

with large numbers of local extrema and difficult

elements such as plateaus and valleys. Evolving

populations can typically get stuck on one of the

local peaks.

Trap Functions: Some of the simplest discrete

analogues of fitness functions with many maxima

are concatenated trap functions (Goldberg, 1987;

Goldberg, Deb, and Horn, 1992). They have been

proven to be GA hard and are of particular interest

from an experimental point of view for testing

algorithm improvements. Here we use fully

deceptive trap functions (Deb and Goldberg, 1993).

A trap function of order k is given by

F(x) = r (k-1-u(x)) / (k-1), if u(x) = k,

where u(x) counts the number of 1-bits in string x;

otherwise F(x) = 1. r<1 denotes the fitness ratio

between optimal and sub-optimal solutions. A

higher-dimensional function can be made by

concatenating n trap functions together. The bit-

string’s fitness is computed as the sum of the

fitnesses of the n traps. The concatenated trap

function has 2n local optima. The global optimum is

a string of all 1’s.

The Royal Road Fitness Functions: Mitchell and co-

workers designed a class of fitness landscapes called

Royal Road functions (RR): R1, R2, R3 and R4

(Mitchell et al., 1992; 1994); (Forrest and Mitchell,

1993). These were specifically designed to test the

“building block” (BB) approach (Goldberg, 1989);

(Holland, 1992), in which a solution can be

decomposed into BBs (which may have genetic

functional relevance), which can be searched

independently and then combined to obtain a good

or even optimal solution. RR have a fixed number of

predetermined schemata, allowing for the study of

GA performance over time. RR are a generalization

of the MaxOnes function: rather than simple

zero/one bitstrings in which the overall count of

ones determines fitness, RR strings have discrete

blocks of sub-sequences of bits, with fitness

evaluated for each block. Royal Staircase (RS) is a

variation of the Royal Road functions, using a

simple landscape with clearly defined neutral layers

(van Nimwegen and Crutchfield, 2000).

Although RR functions were designed to study

GA, some features of the RR functions, especially

R3 and R4, are reminiscent of known aspects of

molecular biological evolution (van Nimwegen and

Crutchfield, 2000, Crutchfield and van Nimwegen,

2001).

3.1 Benchmark Tests

We chose RR-type and trap functions for benchmark

performance tests of our approach versus standard

GA: they reflect many of the significant properties

of biological evolutionary searches and are well-

studied and sufficiently simple to permit statistical

analysis, allowing for comparison between

theoretical expectation and the results of

experimental runs.

The same suite of programs was used to run both

trap and RR function tests. Our package allows a

choice of either the RC or the GRC operators, and

also supports the two alternative reproduction

strategies, RStr1 and RStr2. The RC operator can

process binary strings with three tags and the

interpretation rules listed in Table 1, or eight tags

and the interpretation rules listed in Table 2. In the

current version of our package, the GRC operator is

incapable of processing tags (it ignores them). For

each of the tested fitness functions, 5 series of

experiments were performed: 3 tags and RStr1; 3

tags and RStr2; 8 tags and RStr1; 8 tags and RStr2;

and the current implementation of the GRC operator

(tags ignored). Outcomes did not depend on the

reproduction strategy.

Rugged Landscapes - Trap Fitness Functions: We

used the same parameters for trap function tests as

van Kemenade (1997). We ran a set of experiments

to characterize the efficiency of the different

approaches on different BB sizes (3, 4, 5, 6, 7 and 8

bits). The number of BBs was adjusted such that the

total length of the bit-string was approximately 40

bits. That is, starting from trap order 3, with 8192

extrema, we increased the trap function to order 8,

with 16 local extrema. We used a fitness ratio of r =

0.7.

In all runs, the search terminated when the

optimal solution was obtained, or when the number

of function evaluations exceeded 500,000. The

initial population size was 4096 strings. All results

(Fig. 3) are averaged over 1000 independent runs.

As seen in Fig. 3, the 3-tag version of the retroGA

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

236

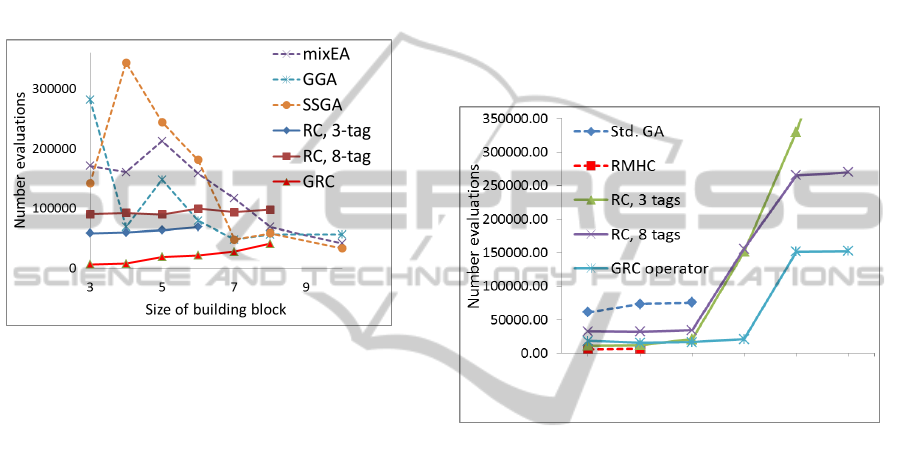
operator is more efficient than the algorithms

(including ‘general’ or standard GA, GGA)

developed by van Kemenade (1997), while the 8-tag

results are not so impressive. To our surprise, the

best performance was achieved by the GRC operator

– some 20 to 50 times faster than standard GA, on

average, for order-3 and order-4 trap functions. We

conclude that elaborate consensus-dependent

operators (standard GA) are not as effective on

rugged landscapes as the more straightforward GRC

operator.

Figure 3: Performance of our approach versus standard

GA. Values indicate number of function evaluations

needed to reach optimum. The results on the mixEA, GGA

and SSGA algorithms are from van Kemenade (1997).

Subbasin-portal Architecture - The RR Fitness

Functions: We tested our approaches on four RR

functions (R1-R4), highlighting different levels of

efficiency to the different functions (Fig. 4). RC, 3-

tag was very efficient for R1-R3, but did not reach

R4-5th level or RS. RC, 8-tag was very impressive

for solving all test functions. In R1-R4, this

approach outperformed standard GA: it was twice as

effective in R1, and even more so in R2 and R3. R4

is well-known to be hard to reach for many

optimization approaches, both evolutionary and non-

evolutionary (Mitchell et al., 1992); (Forrest and

Mitchell, 1993); (Mitchell et al., 1994). The RC, 8-

tag approach, however, achieved the fourth level of

R4 in approximately 30% of runs. Neither Standard

GA, nor Random-Mutation Hill-Climbing (RMHC)

reached the 4th (or 5th) level within the maximum of

function evaluations (Forrest and Mitchell,

1993). In 4% of cases, RC, 8-tag reached the fifth

level of the R4 test, a success rate unprecedented in

the EC literature.

Surprisingly, it was the GRC operator that ended

up being the most effective of all the strategies

tested. Notably, its performance on R1 approached

the non-evolutionary RMHC algorithm (which is not

successful on the higher test functions). For R1, it

was only three times less effective than RMHC (or

even two times, depending on operator parameters),

while RMHC outperformed standard GA by a factor

of 10. The GRC operator achieved the fourth level

of the R4 test in 98% of the runs, and the fifth level

in 67%. With the GRC operator, we have found an

evolutionary approach that outperforms standard GA

by a factor of 3 to 4 on all RR functions. GRC

operator success rates on R4 were unprecedented.

For the RS test function, the 8-tag strategy found the

answer twice as fast, on average, than standard GA,

while the GRC operator was more than three times

faster than GA (Fig. 4).

Figure 4: Performance of our approaches (RC & GRC

operators) versus standard GA (Std. GA) and Random-

Mutation Hill-Climbing (RMHC) on the Royal Road

family functions. Values indicate number of function

evaluations needed to reach optimum, averaged over 1000

runs. R4

and R4

are the 4

and the 5

level of the R4,

respectively. It takes >500,000 evaluation to solve the RS

problem by Std. GA and RC, 3-tag.

Comparison of Figs. 3 and 4 indicates that the

retroGA-with-tags approaches are more effective on

subbasin-portal functions (RR-type, versus trap

functions). We can hypothesize that these models

have picked up some of the crucial features of real

molecular recombinatorial mechanisms which

operate within such architectures.

We conclude that there is a fundamental

difference in the quality of artificial recombination

implemented by the GRC operator and by the

standard GA crossover operator. The positions of the

sites of crossover and exchange between two strings

in computational GA are chosen randomly.

However, in biology, crossover occurs at sites of

high homology between two molecules of nucleic

acid. These regions of high homology may be

naturally interpreted as BBs. As such, crossover

R1 R2 R3 R4

RETROVIRAL GENETIC ALGORITHMS - Implementation with Tags and Validation Against Benchmark Functions

237

operations in the natural world do not destroy BBs,

but instead conserve them wholly; it is the material

between the BBs that undergoes crossover

exchanges and point mutations. It is well-known that

the destruction of already-discovered BBs by

crossover operators is one of the major problems

with standard GA (originally shown through

experiments with RR functions). Because of this, the

ability of homology-based mechanisms (e.g. sex-

based polymerase chain reaction) to conserve

already located BBs is of tremendous interest to us.

The longer-term goals of our project are to

develop the retroGA approaches such that we can

more clearly gauge their utility to computer science

in general, as well as in such practical applications

as in vitro molecular evolution and biomolecular

computation. In recent decades, computational GA

has become an effective mathematical instrument for

modelling and analyzing the processes and

mechanisms of biological evolution. As retroGA is

for the most part domain-independent, it can readily

be applied to all forms of EC, for example greatly

assisting in solving problems on the selection of

macromolecules with properties that do not exist in

the natural world.

ACKNOWLEDGEMENTS

This work was supported by Joint NSF/NIGMS

BioMath Program, 1-R01-GM072022 and the

National Institutes of Health, 2R56GM072022-06.

REFERENCES

Barbour A. G., and Restrepo B. I., (2000). Antigenic

variation in vector-borne pathogens. Emerg Infect Dis.

6: 449-457.

Crutchfield, J. P. and van Nimwegen, E., (2001). The

Evolutionary Unfolding of Complexity. In Evolution

as Computation, DIMACS workshop, Springer-Verlag,

New York.

Deb, K. and Goldberg, D. E., (1993). Analyzing deception

in trap functions In D. Whitley (Ed.), Foundations of

Genetic Algorithms, pp. 93-108.

Donelson J.E. (1995). Related Mechanisms of antigenic

variation in Borrelia hermsii and African

trypanosomes. J Biol Chem. 270:7783-7786.

Forrest S. and Mitchell M., (1993) Relative building-block

fitness and the buildingblock hypothesis. In D.

Whitley (ed.), Foundations of Genetic Algorithms 2,

109-126. San Mateo, CA: Morgan Kaufmann.

Galetto R. and Negroni M., (2005), Mechanistic features

of recombination in HIV. AIDS reviews 7 (2: 92-102.

Goldberg D. E., (1987). Simple genetic algorithms and the

minimal deceptive problem. In L. Davis, editor,

Genetic Algorithms and Simulated Annealing, pp. 74-

88. Pitman, London.

Goldberg, D. E., (1989). Genetic Algorithms in Search,

Optimization, and Machine Learning. Addison-

Wesley, Reading, Massachusetts.

Goldberg D. E., Deb K., and Horn J., (1992). Massive

multimodality, deception, and genetic algorithms, In:

Parallel Problem Solving from Nature, 2, pp. 37-46.

Holland, J. H., (1992). Adaptation in natural and Artificial

Systems: an introductory analysis with applications to

biology, control and artificial intelligence. MIT Press.

Kauffman S. A. and Levin S., (1987). Towards a general

theory of adaptive walks on rugged landscapes. J.

Theor. Biol., 123:11-45.

Kemenade C. H. M., van, (1997). The Mixing

Evolutionary Algorithm, independent selection and

allocation of trials. In Proceedings of the IEEE

international conference on evolutionary computation,

1997, p. 13-18.

Lewin, B. (2003). Genes VIII. 1056 p.

Mitchell M., Forrest S., and Holland J. H., (1992). The

Royal Road for genetic algorithms: Fitness landscapes

and GA performance. In Proceedings of the First

European Conference on Artificial Life. Cambridge,

MA: MIT Press/Bradford Books.

Mitchell M., Holland J., and Forrest S., (1994) When Will

a Genetic Algorithm Outperform Hill Climbing? In J.

Cowan, G. Tesauro, and J. Alspector, Advances in

Neural Information Processing Systems, Morgan

Kauffman, San Francisco, CA.

Negroni M. and Buc H., (2001). Mechanisms of retroviral

recombination. Annu Rev Genet. 35: 275-302.

Nimwegen E, van, and Crutchfield, J. P., (2000).

Metastable Evolutionary Dynamics: Crossing Fitness

Barriers or Escaping via Neutral Paths? Bulletin of

Mathematical Biology 62: 799-848.

Spirov A. V., Kazansky A. B., Zamdborg L., Merelo J. J.,

Levchenko V. F., (2009), Forced Evolution in Silico

by Artificial Transposons and their Genetic Operators:

The John Muir Ant Problem CoRR abs/0910.5542

Spirov A. V. and Holloway D. M., (2010) Design of a

dynamic model of genes with multiple autonomous

regulatory modules by evolutionary computations.

Procedia Computer Science 1(1): 1005-1014.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

238