
HYBRID ALGORITHM FOR FUZZY MODEL PARAMETER
ESTIMATION BASED ON GENETIC ALGORITHM AND
DERIVATIVE BASED METHODS
A. Lavygina
and I. Hodashinsky
Department of Data Processing Automation, Tomsk State University of Control Systems and Radioelectronics
40 Lenina Street, Tomsk, Russian Federation
Keywords: Fuzzy Modeling, Parameter Estimation, Hybrid Algorithm, Genetic Algorithm, Gradient Descent Method,
Kalman Filter, Least Squares Method.
Abstract: Hybrid method for estimation of fuzzy model parameters is presented. The main idea of the method is to
apply gradient descent method or Kalman filter as a mutation operator of genetic algorithm for estimation of
antecedent parameters of fuzzy “IF-THEN” rules. Thus, part of the individuals in the population mutate by
means of gradient descent method or Kalman filter, the others mutate in an ordinary way. Once antecedents
are tuned, consequents tuning is performed with the least squares method. The results of computer
experiment are presented.
1 INTRODUCTION
Input-output representation mapping in fuzzy
models is presented as a set of fuzzy “if-then” rules.
Each rule consists of two parts: antecedent and
consequent. An antecedent (conditional part)
contains a statement regarding input variables
values, while a consequent presents the value that
output variable takes. The rules for single fuzzy
model are as follow:
Rule i: IF x
1
= А
1i
AND x
2
= А
2i
AND… AND
x
m
= А
mi
THEN
y = r
i
,
where A
ji
is a linguistic term to evaluate variable x
j
,
while output y is evaluated by real number r
i
.
The model performs the mapping
ℜ→ℜ
m
F :
,
substituting fuzzy conjunction operator by product,
and fuzzy rules aggregation operator is replaced by
addition. Mapping F for singleton type model is
defined by the formula:
()
∑
⋅⋅⋅
∑
⋅⋅⋅⋅
=
=
=
n
i
m
mi
A
i
A
i
A
n
i
im
mi
A
i
A
i
A
xxx
rxxx
F
1
2
2
1
1
1
2
2
1
1
)(...)()(
)(...)()(
μμμ
μμμ
x
(1)
where
mT
m
xx ℜ∈= ],...,[
1
x , n is the number of
fuzzy model rules, m is the number of input
variables in the model,
)(
jA
x
ji
μ
is a membership
function of j-th variable to term A
ji
.
2 FUZZY IDENTIFICATION
The problem of fuzzy identification is the following:
the results of observations of input and output
variables of the system must be designed in optimal
fuzzy model. Optimality criterion is the smallest
error.
In the initial phase of fuzzy model tuning before
using parameter estimation algorithms it is necessary
to identify the fuzzy model structure and initial
values for antecedent parameters and rules
consequents.
Parameter estimation is carried out by two types
of methods: 1) methods based on derivatives (least
squares method, gradient descent method, Kalman
filter), 2) metaheuristics (genetic algorithm,
algorithm of ants colony, particle swarm method,
simulated annealing method and search with bans).
Derivative based methods are more accurate but can
get stuck in local minimums. Metaheuristic methods
are more stable, but require more time resources.
513
Lavygina A. and Hodashinsky I..
HYBRID ALGORITHM FOR FUZZY MODEL PARAMETER ESTIMATION BASED ON GENETIC ALGORITHM AND DERIVATIVE BASED METHODS.
DOI: 10.5220/0003690605130515
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 513-515
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

3 HYBRID ALGORITHM
Hybrid algorithm allows to combine advantages of
both metaheuristics and derivative based methods.
This association will enhance the quality of
decisions compared to using methods individually.
Hybrid algorithm based on genetic algorithm and
derivative based methods (gradient descent method,
Kalman filter, least squares method) has been
developed. The following hybridization technique is
suggested. At the first stage, least squares method is
used to adjust consequents parameters. Then,
modified genetic algorithm is started. The essence of
the modification is in applying gradient descent
method or Kalman filter together with mutation
operator of the genetic algorithm to tune antecedent
parameters. In doing so, part of the individuals in the
population change with gradient descent method or
Kalman filter. Such mutation take place with a
probability p
′
(p
′
∈ (0, p), where p – probability of
individual mutation). The other individuals are
subject to mutation with the probability p-p
′
by
means of random one-point or multipoint mutation.
Once antecedents are tuned, consequents tuning is
performed with least squares method.
4 SIMULATION RESULTS
The idea of the experiment was to use fuzzy model
for approximation of the following test functions:
a)
()()
]5;5[,,2sin2sin),(
212121
−∈⋅= xxxxxxf
ππ
b)
].2/;2/[,),sin(),(
212121
ππ
−∈⋅= xxxxxxf
Based on test functions, the tables of 121 lines
were built and then, using these tables training of
fuzzy models was carried out. Triangular-shaped
membership functions are considered for each
variable.
Figure1 shows the results of the suggested hybrid
algorithm and separate methods used for selected
test functions. In the left column of the histogram
the mean-square error (MSE) of initial solution is
given, the other columns correspond to the averaged
values of MSE of the fuzzy model for each of the
algorithms.
LSM 0,00312
hybrid 0,0000
2
initial 0,05799
GA 0,00083
SAA 0,00124
KF 0,00052
GM 0,00379
a)
GA 0,00009
LSM 0,00037
initial 0,01372
SAA 0,00024
KF 0,00052
GM 0,00379
hybrid 4,269 E-0
9
b)
Figure 1: Experiment results for test functions a)-b) (GA –
genetic algorithm, SAA – simulated annealing algorithm,
LSM– least squares method, GM – gradient descent
method, KF – Kalman filter, hybrid– suggested hybrid
algorithm).
The results of the experiment allow to conclude
that the suggested hybrid algorithm provides better
results than each method separately.
To compare the developed hybrid algorithm with
the existing methods of building fuzzy models, the
study of approximation results was carried out for
the nonlinear functions presented in table 1.
The values of mean-square approximation error,
obtained with the developed algorithm and
analogues for these functions are shown in table 2.
Considering the obtained results, it is possible to
conclude that the suggested hybrid algorithm in most
cases yields fewer errors compared to the existing
analogues.
Table 1: Data sets considered in experimental analysis.
Test Function
Number of
Observation
c)
(
)
(
)
()
]1;0[,
1,0
)5,1/(125sin
)7,0(100exp101)(
2
∈
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
⋅
⋅−⋅−⋅+=
x
x
x
xxf
100
d)
]5;1[,
,)1(),(
21
25,1
2
2
121
∈
++=
−−
xx
xxxxf
400
e)
]5;5[,
,
2
sin
2
sin),(
21
21
21
−∈
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
xx
xx
xxf
ππ
441
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
514
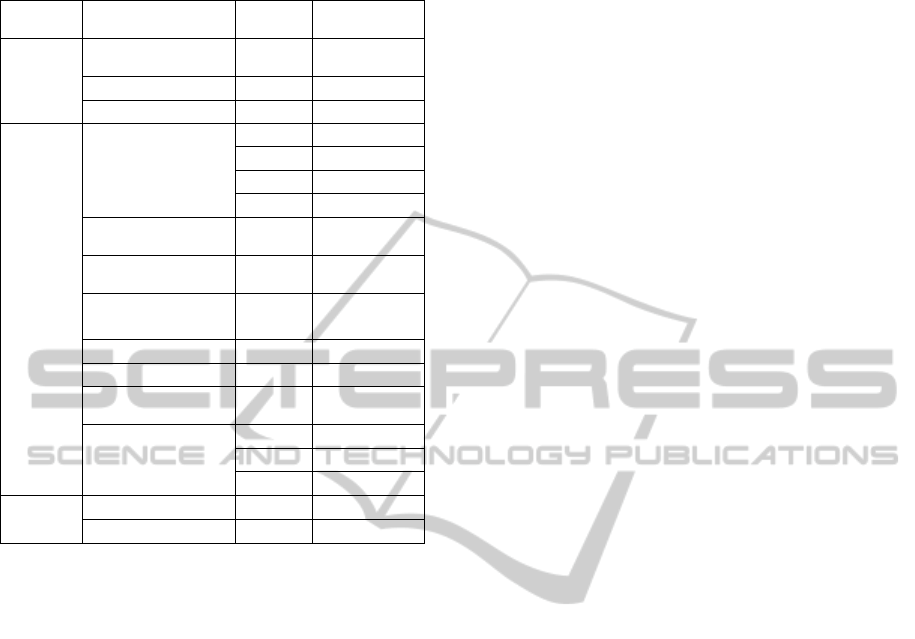
Table 2: MSE values obtained with the proposed hybrid
algorithm and other authors’ algorithms.
Function Algorithm
Number
of Rules
MSE
c
(Mitaim et al.,
1996)
12 1.426
(Lisin et al., 1999) 12 0.247
Hybrid algorithm 12 0.0169
d
(Rojas et al., 2000)
9 0.146
16 0.051
25 0.026
36 0.017
(Sugeno et al.,
1993)
6 0.079
(Nozaki et al.,
1997)
25 0.0085
(Teng et al., 2004) 4 0.016
(Lee, 2008) 3 0.0028
(Wang et al,. 2005) 3 0.0052
(Tsekouras et al.,
2005)
6 0.0108
Hybrid algorithm
9 0.0168
16 0,0018
25 0.0002
e
(Lee, 2008) 25 less than 0.001
Hybrid algorithm 25 0.00009
5 CONCLUSIONS
The results of the experiment allow to conclude that:
• The suggested hybrid algorithm based on genetic
algorithm and derivative based methods provides
better results than each method separately;
• The suggested hybrid algorithm for fuzzy models
tuning allows to achieve smaller error values in most
cases compared to existing analogues.
ACKNOWLEDGEMENTS
This paper is supported by Russian Foundation for
Basic Research (09-07-99008).
REFERENCES
Mitaim, S., Kosko, B., 1996. What is the best shape for a
fuzzy set in function approximation? In Proc. Fifth
IEEE Int. Conf Fuzzy Systems, vol. 2. New Orleans
Lee, Zne-Jung, 2008. A novel hybrid algorithm for
function approximation. Expert Systems with
Applications, vol. 34.
Lisin, D., Gennert M.A., 1999. Optimal Function
Approximation Using Fuzzy Rules. In Proc. Int. Conf.
North American Fuzzy Information Processing
Society.
Rojas, I., Pomares, H., Ortega, J., Prieto, A., 2000. Self-
organized fuzzy system generation from training
examples. In IEEE Transactions on Fuzzy Systems,
vol. 8 (1).
Nozaki, K., Ishibuchi, H., Tanaka H., 1997. A simple but
powerful method for generating fuzzy rules from
numerical data. In Fuzzy Sets and Systems, vol. 86.
Sugeno, M., Yasukawa, T., 1993. А fuzzy-logic-based
approach to qualitative modeling. In IEEE
Transactions on Fuzzy Systems. vol.1, no. 1.
Teng, Y., Wang, W., Chiu, C.H., 2004. Function
approximation via particular input space partition and
region-based exponential membership functions. In
Fuzzy Sets and Systems, vol. 142.
Tsekouras, G., Sarimveis, H., Kavakli, E., Bafas G., 2005.
A hierarchical fuzzy-clustering approach to fuzzy
modeling. In Fuzzy Sets and Systems, vol. 150.
Wang, H., Kwong, S., Jinb Y., Wei, W., Man, K.F., 2005.
Multi-objective hierarchical genetic algorithm for
interpretable fuzzy rule-based knowledge extraction.
In Fuzzy Sets and Systems, vol. 149.
HYBRID ALGORITHM FOR FUZZY MODEL PARAMETER ESTIMATION BASED ON GENETIC ALGORITHM
AND DERIVATIVE BASED METHODS
515
