ELECTROCARDIOGRAM DERIVED RESPIRATION USING AN

EVOLUTIONARY ALGORITHM

Jakob Juul Larsen, Lars G. Johansen and Henrik Karstoft

Electrical and Computer Engineering, Aarhus School of Engineering, Aarhus University

Dalgas Avenue 2, 8000 Aarhus C, Denmark

Keywords:

Electrocardiogram Derived Respiration, Evolutionary Algorithms, ECG Modeling.

Abstract:

In this work we present a method to extract the respiratory signal from single lead ECG measurements, electro-

cardiogram derived respiration (EDR). The method is based on adaptive ECG modeling and respiratory signal

estimation using an evolutionary algorithm fed with the model parameters. The evolutionary algorithm, which

is allowed to employ a large constellation of functions, comes up with a set of relatively simple expressions

(3-4 terms) describing valid relationships between ECG model parameters and the respiratory signal. In fact,

the expressions mainly turn out to be linear combinations of the model parameters. Our preliminary experi-

ments indicate that this method yields a robust EDR, and that this EDR correlates very well with a reference

respiratory signal measurement. Correlation coefﬁcients for the derived expressions lie around 0.95.

1 INTRODUCTION

Healthcare at Home is a ﬁeld that will show signif-

icant growth over the next decades. This growth is

mainly driven by economic issues and health related

concerns (e.g. monitoring elderly people in their own

homes). An expected consequence of this is an in-

crease in the demand for telemedicine devices for re-

mote monitoring of physiological parameters.

It is well known that a variety of physiologicalsig-

nals and parameters can be derived from ECG mea-

surements, e.g. Heart Rate Variability (HRV). An-

other derivation is the respiratory signal, on which

we will focus in this work. Monitoring the respira-

tory signal can enable detection of sleep related symp-

toms such as central and mixed apnea, hypopnea, and

tachypnea, see (Raymond et al., 2000).

Deriving as many physiological signals and pa-

rameters as possible from as few body sensors as pos-

sible is generally desirable. Primarily in order to min-

imize user discomfort but also in order to minimize

cost and hardware complexity of the monitoring sys-

tem.

Respiratory signals can be measured using dedi-

cated devices but in order to keep the number of body

sensors low it would be advantageousto simply derive

the signal from ECG measurements using the existing

ECG sensors.

Derivation of the respiratory pattern from the ECG

signal is possible when the ECG is directly avail-

able. For healthy subjects, the normal respiratory cy-

cle modulates the heart rate, essentially determined

as the RR-distance in successive PQRST complexes,

and this modulation causes what is known as Respi-

ratory Sinus Arrhythmia (RSA), see (Clifford et al.,

2006a) and (Grossman and Wientjes, 1986). Typ-

ically, inhalation leads to cardio-acceleration, i.e. a

decrease in the RR rate of distance, and exhalation

causes cardio-deceleration. Similarly, the morpho-

logy of the PQRST complex is also affected by the

respiration, i.e. the wave amplitudes and the distances

between the different waves oscillates synchronously

with the respiration cycle.

In this work we will present a novel technique to

extract the respiratory signal from single lead ECG

measurements. Among other objectives, this tech-

nique aims at producing a robust RSA estimate as

an input parameter to bio-feedback systems. For ex-

ample, anxiety patients can make use of information

about their respiration presented to them in real time

in order to control the breathing. For patients suffer-

ing anxiety related disorders, controlled breathing can

be an important tool in diminishing the psychological

effects of sudden anxiety attacks.

147

Juul Larsen J., G. Johansen L. and Karstoft H..

ELECTROCARDIOGRAM DERIVED RESPIRATION USING AN EVOLUTIONARY ALGORITHM.

DOI: 10.5220/0003696101470152

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 147-152

ISBN: 978-989-8425-89-8

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 ECG DERIVED RESPIRATION

It is well known that the respiration signal can be de-

rived from the ECG signal. It is reported in the liter-

ature that respiration signal correlates to the changes

in the heart rate as well as changes in the morphology

of the PQRST complex. In the literature this is known

as ECG Derived Respiration (EDR). Many signal pro-

cessing methods have been derived to calculate the

EDR. For example in (Moody et al., 1985) the map-

ping from the ECG to the respiratory signal is given

by the area of the normal QRS complex.

(Mazzanti et al., 2003) propose a method for EDR

based on QRS areas in an 8 lead ECG measurement

setup. They ﬁnd some limitations in the validity of

the EDR data, one important observation to mention

is that the sampling frequency of the ECG signal has

to be at least 500Hz, but still suggest the method as

being effective, for example in telemetric monitoring.

Recently, (O’Brien and Heneghan, 2007) com-

pared different algorithms for deriving the respira-

tory signal from single lead recorded ECGs compared

to a reference respiratory signal measurement based

on inductance plethysmography. One of the methods

applies interpolation between R wave amplitudes in

successive complexes. This technique is sensitive to

baseline wander, however they ﬁnd a correlation coef-

ﬁcient at 0.78 which indicates that the technique may

be useful.

(Sobron et al., 2010) have also evaluated diffe-

rent methods for estimating EDR. Their comparative

study included complex morphology such as the QRS

area and amplitudes as well as heart rate variability.

They suggest that combining EDR based on more of

these ECG derivations gives the best respiratory fre-

quency estimation.

This result probably does not come as a complete

surprise, and hence leads us to take this combination

method a step further, letting a evolutionary algorithm

map a large set of parameters representing the ECG

complexes into a respiratory signal.

3 EVOLUTIONARY ALGORITHM

Evolutionary algorithms have been known in the sci-

entiﬁc community since the late 1960 early 1970,

where John Holland introduced the basic idea. An

evolutionary algorithm is a randomized population-

based search technique, inspired by evolution princi-

ples from biology. Since its conception the paradigm

has been widely used in engineering and computer

science i.e. in computer programming, artiﬁcial intel-

ligence and optimization.

A specialized implementation of evolutionary al-

gorithms optimizes the symbolic regression problem.

In this problem the search space consists of symbolic

mathematical expressions, and the cost function for

minimizing, is a chosen error metric. The error met-

ric measures the residue between the estimate derived

from the symbolic expression and the real data (Koza,

1992).

A symbolic regression solver has been imple-

mented by (Schmidt and Lipson, 2009) in the appli-

cation Eureqa, which is freely available online on the

web. In our work we used Eureqa as a black box to

model the mapping from the ECG to the respiration

signal, in search for a more precise and robust esti-

mate of the EDR mapping.

4 EXPERIMENTAL METHODS

The ECG signal and the respiratory signal are si-

multaneously recorded by a commercially available

Zephyr Bioharness chest worn belt, (Zephyr Biohar-

ness, nd). The respiratory signal is measured with a

closed-source mechanical sensor. The sampling fre-

quency for the respiratory signal is 17.86 Hz (T=56

ms). The ECG signal is sampled at 250 Hz. All sig-

nals are recorded with the software supplied with the

Zephyr Bioharness. Some pre-processing of the ECG

signal, i.e. ampliﬁcation and ﬁltering are done au-

tomatically by closed-source systems in the Zephyr

device. All subsequent processing of the ECG and

respiratory signals are carried out in MATLAB (MAT-

LAB, 2010).

The ECG signal is often corrupted by small

amounts of nonstationary 50 Hz interference. This

noise is removed after signal acquisition with stan-

dard adaptive noise cancelling using a synthetic 50

Hz reference. Before modeling the ECG signal is seg-

mented into heartbeats. The location of each heartbeat

is found with an open source Pan-Tompkins algorithm

(Clifford et al., 2006b). The 250 Hz sampling fre-

quency of the ECG device is too low to ensure stable

modeling of the QRS complex (Clifford et al., 2006a).

This problem is counteracted by upsampling and in-

terpolation of the ECG signal to 1500 Hz before mod-

eling.

A typical heartbeat is shown in ﬁgure 1 along with

the mathematical model discussed below. The QRS

complex and the T wave are clearly visible. The P

wave is normally barely visible above the noise ﬂoor

on the recorded electrocardiograms. Therefore no at-

tempt has been made of using information from the P

wave in this work.

A large number of parameters can be extracted

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

148

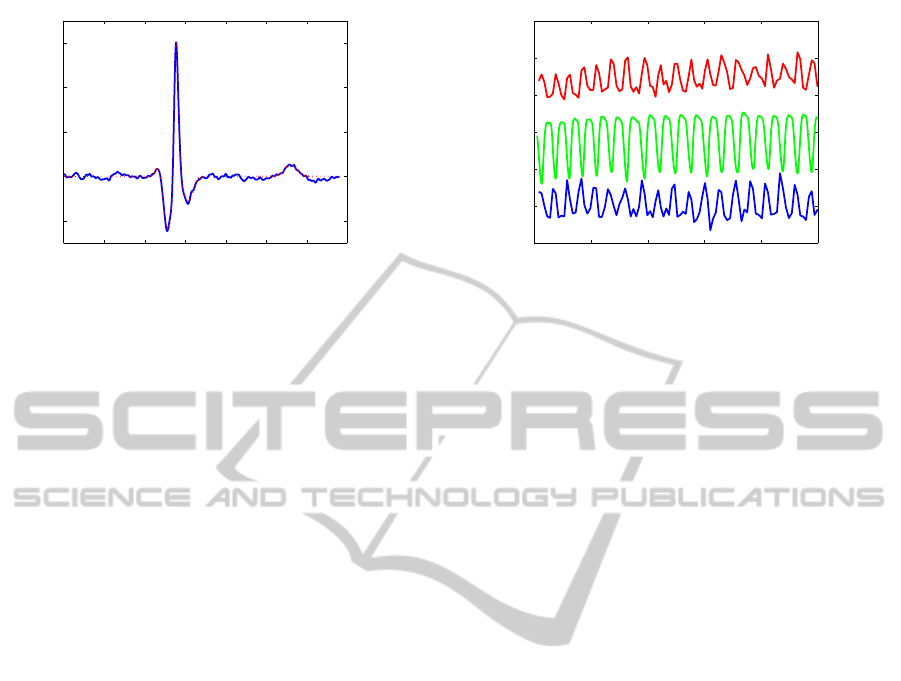
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

−50

100

150

time [s]

amplitude [a.u.]

Figure 1: An example of a recorded heartbeat (blue) and the

corresponding model (red).

from a single heartbeat i.e. amplitudes, areas and

shapes of the individual waves in the heartbeat as well

as the relative position between the waves. These pa-

rameters can be estimated directly from the recorded

ECG signals. To minimize the inﬂuence of mea-

surement noise each heartbeat is ﬁtted to a model-

heartbeat and the parameters are extracted from the

mathematical model.

The mathematical model of the ECG signal con-

sists of 3 Gaussians with positive amplitude and 2

Gaussians with negative amplitude. The two nega-

tive amplitude Gaussians model the Q and S wave.

The positive amplitude Gaussians model the small

peak preceding the Q wave and the R and T waves

respectively. In related work (Clifford et al., 2006a)

an asymmetric T wave is modeled with two positive

Gaussian peaks. However, the T wave signal from

the Zephyr Bioharness is quite symmetric and, except

from a small baseline dip, well modeled by a single

Gaussian. The parameters of the model are found by

Levenberg-Marquardt ﬁtting using MATLAB’s Opti-

mization Toolbox (MATLAB, 2010).

An example of a heartbeat and the correspond-

ing model is shown in ﬁgure 1. The model captures

the important features of the QRS complex and the T

wave well and discards the major part of the noise.

For each heartbeat a signal to noise ratio is measured

with signal being deﬁned as the energy in the model

signal and noise being deﬁned as the energy in the

difference between the experimental signal and the

model signal. The signal to noise ratio is normally

found to be in the 70-130 range. If heartbeats with

signal to noise ratios lower than 10 are found, they

are labeled as noisy and discarded.

Each heartbeat is matched with the corresponding

output from the respiratory sensor at the appropriate

time. The maximum of the R wave is deﬁned as the

time zero for each heartbeat and the respiratory sam-

ple closest in time is chosen as the value of the respi-

0 20 40 60 80 100

time [s]

amplitude [a.u.]

Figure 2: Examples of typical measurements. The data are

vertically translated and scaled for clarity. The top curve

(red) shows the the amplitude of the R wave, the middle

curve(green) shows the respiratory signal, and the bottom

curve (blue) shows the distance between the peaks of the R

and S waves.

ratory signal. Due to the low sampling rate this proce-

dure leads to small errors in the value of the respira-

tory signal when this signal is changing quickly. The

maximum error is found to be smaller than 2%.

A number of parameters can be extracted from

the mathematical model of the heartbeat. Many of

these parameters will, however, be highly correlated.

An example of this is shown in ﬁgure 2 where three

parameters from a typical experiment are plotted; R

wave amplitude, the distance between the maximum

and minimum of the R and S waves and the respira-

tory signal. The R wave amplitude and R-S distance

are seen to oscillate in anti-phase with the respiratory

signal.

In this work where the goal is to let an evolu-

tionary algorithm decide the optimum combination of

ECG derived parameters for EDR the following pa-

rameters are extracted from each heartbeat: The am-

plitude, area and width, deﬁned by full width at half

maximum, for the Q, R, S and T waves together with

the distances between the maxima of the Q and R

waves, the R and S waves and the S and T waves as

shown in table 1. Due to the low sampling rate and

build-in ﬁltering function of the Zephyr Bioharness

no attempt have been made of extracting asymmetry

parameters of the waves.

All the extracted parameters have non-zero mean

values and numerically quite different values. All

ECG derived parameters are put on equal footing be-

fore they are used in the evolutionary algorithm by

subtracting their mean values and subsequently nor-

malizing the maximum value to one. Similarly, the

mean value is subtracted from the respiratory signal.

A number of possibilities exist for the ﬁtness met-

ric for the evolutionary algorithm i.e. mean absolute

error, mean square error, correlation coefﬁcient, me-

ELECTROCARDIOGRAM DERIVED RESPIRATION USING AN EVOLUTIONARY ALGORITHM

149

Table 1: List of model parameters derived from the ECG

signal and the absolute value of the linear correlation with

the respiratory signal.

Parameter |ρ|

amp

0.43± 0.03

area

0.31± 0.04

fwhm

0.36± 0.01

amp

0.88± 0.01

area

0.83± 0.01

fwhm

0.17± 0.01

amp

0.21± 0.02

area

0.86± 0.01

fwhm

0.79± 0.01

amp

0.80± 0.01

area

0.81± 0.01

fwhm

0.08± 0.01

distance

0.59± 0.01

distance

0.67± 0.01

distance

0.59± 0.02

dian error etc. In this work the optimization is done

with respect to the correlation coefﬁcient similar to

the work of (O’Brien and Heneghan, 2007). The

search for the optimized connection between the ECG

derived parameters and the respiration signal can be

restricted by only allowing the evolutionary algorithm

to use a limited number of mathematical functions.

In this work addition, subtraction, multiplication and

division are used as building blocks unless otherwise

speciﬁed. The evolutionary algorithm is run on a stan-

dard dual core 2 GHz pc and each search is typically

run for 2-3 hours on data sets containing approxi-

mately 500 heartbeats.

The ECG and respiratory sensors in the Zephyr

Bioharness are sensitive to movement artifacts, there-

fore, the subject under investigation is seated in a

standard ofﬁce chair, instructed to sit still, keep quiet

and breathe steadily during the recording of the data.

This procedure is found to be sufﬁcient to minimize

artifacts to below a visible threshold. This procedure

also has the beneﬁt of providing stationary data for

the evolutionary algorithm to work with in this proof

of concept investigation.

5 RESULTS

In a brute-force approach, all ECG derived parame-

ters should be feed immediately to the evolutionary

algorithm. It is, however, instructive to initially in-

clude only a limited amount of selected parameters

and subsequently include further parameters. This ap-

proach allows for a comparison with different meth-

ods described in the literature and potentially a better

understanding of the underlying mechanisms. In the

following sections a number of increasingly complex

optimization experiments are described.

5.1 Peak Amplitude

Under normal circumstances the peak amplitude of

the ECG signal is given by the maximum of the R

wave. This easily extracted parameter is known to

be correlated with the respiratory signal and a num-

ber of authors have used this feature to form an EDR

estimate, see e.g.(Clifford et al., 2006a) for a review.

Figure 2 shows a similar correlation between the am-

plitude of the R wave and the respiratory signal in our

experiments. Whether a higher degree of linear corre-

lation can be found by some nonlinear function of the

R wave amplitude isn’t obvious. A nonlinear relation

can originate in both the physical mechanisms con-

necting respiration and the heart beat morphology or

in inherent nonlinearities in the sensors used to mea-

sure the ECG and respiratory signal.

For the particular dataset investigated the corre-

lation coefﬁcient between the normalized R wave

amplitude, R

amp

, and the respiratory signal is |ρ| =

0.88 ± 0.01. The uncertainty is estimated by the dif-

ference of ρ for the two parts of the data set used for

training and validation by the evolutionary algorithm.

When run with only addition, subtraction, mul-

tiplication and division as the mathematical build-

ing blocks for the evolutionary algorithm, the high-

est correlation found among the suggested solutions

is |ρ| = 0.89 ± 0.01 for the expression

EDR = − R

amp

1+ R

amp

4+ 24R

amp

+ 108R

amp

+ 216R

amp

+ 162R

amp

(1)

When the search space is increased to include con-

stant values, power functions, exponential and loga-

rithmic combinations and sine and cosine terms the

solution with the highest correlation coefﬁcient (|ρ| =

0.90± 0.01) is given by the expression

EDR =sin(0.335− 2.22R

amp

)

× cos

−0.0477

0.177− 2.58R

amp

+ 5.91R

amp

(2)

The conclusion of this experiment is therefore that

when only the R wave amplitude is available, no sim-

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

150

ple nonlinear function of this parameter gives a sig-

niﬁcantly better correlation with the respiratory signal

than the R wave amplitude alone.

5.2 Peak-to-peak Amplitudes

A hardware based EDR technique has been presented

by (Dobrev and Daskolov, 1998). The main idea is

to ﬁnd the maximum and minimum value of the ECG

in each heartbeat, the rationale being that the max-

imum and minimum value can be found with stan-

dard electronic hardware. The two extremum values

are subsequently squared, summed and smoothed by

a low-pass ﬁlter to provide the EDR signal.

In the work by Dobrev and Daskalov the maxi-

mum and minimum of the ECG signal are found at the

R wave and the S wave. However, the typical ECG

signal recorded with the Zephyr Bioharness have its

minimum at the Q wave and the optimization of a

peak-to-peak based EDR signal should therefore done

with the R and Q wave amplitudes.

When the evolutionary algorithm is run with R

amp

and Q

amp

as inputs the algorithm mainly evolves to a

number of quite elongated expressionsand one simple

expression

EDR = R

amp

(3)

With a correlation coefﬁcient of |ρ| = 0.90 ± 0.01

which is slightly better than the correlation between

the respiratory signal and the R wave amplitude by it-

self. If the peak-to-peak amplitude, R

amp

+ Q

amp

, is

used directly to form the EDR estimate, the correla-

tion diminishes to 0.75±0.02.

5.3 Peak Amplitudes

Previous work by (Raymond et al., 2000) have

demonstrated that an EDR signal can be extracted

from the T wave. The EDR estimate was derived from

an averaged amplitude of the T wave. A natural ex-

tension of the peak-to-peak amplitude based EDR is

a search where the input is the amplitude of all peaks

present in the recorded signal i.e. the amplitude of the

Q, R, S and T waves. The correlation coefﬁcients be-

tween the different wave amplitudes and respiratory

signal are shown in table 1.

The output from the evolutionary algorithm is

again a number of primarily rather long expressions.

However, one of the expressions is quite simple

EDR = Q

amp

+ 4R

amp

+ S

amp

+ T

amp

(4)

This EDR estimate has a correlation coefﬁcient of

0.93± 0.01 and for this particular dataset we can con-

clude that the evolutionary algorithm devices an im-

proved EDR estimate compared to the standard meth-

ods of both R wave and amplitude and peak to peak

amplitude.

The improvement of the correlation if one of long

expressions is used for the EDR estimate is insigniﬁ-

cant and well within the uncertainty limits.

5.4 All Parameter Search

The ﬁnal experiment is to feed all parameters derived

from the ECG signal to the evolutionary algorithm.

Due to the increased number of available parameters

to combine, an improvement in the maximum corre-

lation is anticipated for the longest expressions. The

key issue is, however, whether a simple combination

will improve the correlation coefﬁcient.

The highest correlation coefﬁcient is found to be

ρ = 0.97± 0.01 for an involved expression contain-

ing fractions and cubic terms. However, a few simple

expressions also give high correlation coefﬁcients i.e.

EDR = ST

distance

− S

area

− R

area

(5)

With ρ = 0.95 ± 0.01 and

EDR = ST

distance

+ Q

area

− R

amp

− 2R

area

(6)

With ρ = 0.96 ± 0.01.

These results shows that for the speciﬁc dataset

used, a high correlation between a simple combina-

tion of ECG derived parameters and the respiratory

signal can indeed be found by a computerized search.

Both EDR estimates make use of ST

distance

and R

area

suggesting that these two parameters are potentially

robust EDR estimators.

5.5 Nonstationary Breathing

A ﬁrst test of the robustness of the EDR estimate has

been performed by recording a time series of ECG

and respiratory signals containing periods of bated

respiration resembling sleep apnea. An example of

this is shown in ﬁgure 3.

The EDR estimate is calculated with Eq (6). From

the ﬁgure it is evident that the EDR estimate captures

the bated respiration. In particular, the stopped res-

piration and restart of respiration is immediately cap-

tured.

6 CONCLUSIONS

The results and their applicability are currently lim-

ited by two major factors. First of all, the study has

not been carried out on a pool of patients. In order to

ELECTROCARDIOGRAM DERIVED RESPIRATION USING AN EVOLUTIONARY ALGORITHM

151

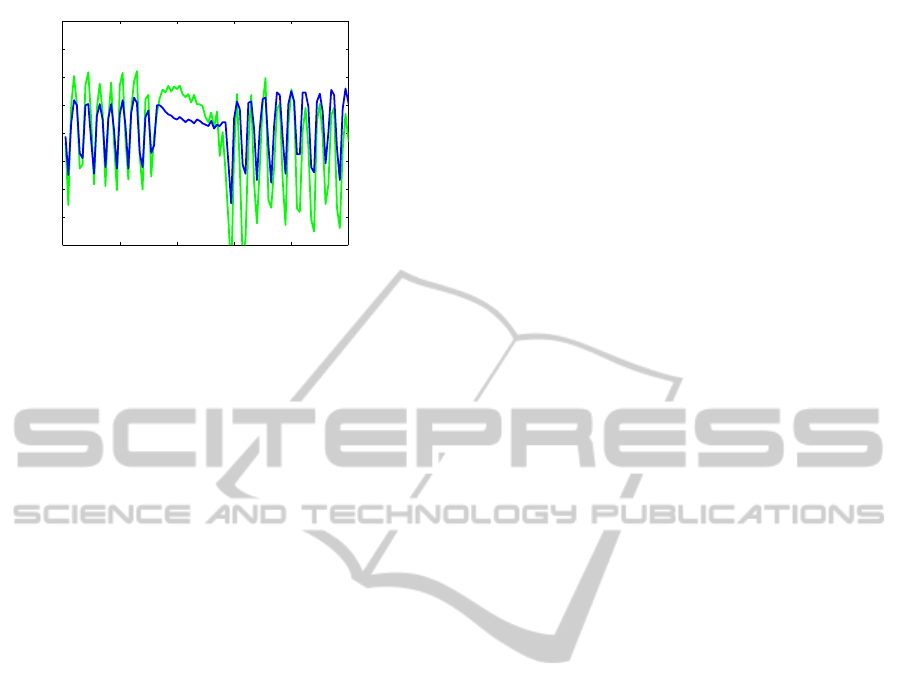
0 20 40 60 80 100

−2

−1.5

−1

−0.5

0.5

1.5

time [s]

amplitude [a.u.]

Figure 3: The graph shows the respiratory signal (blue) and

the EDR signal (green) for a subset of a timeseries contain-

ing periods of deep breathing and periods with bated respi-

ration.

demonstrate the robustness of this EDR approach the

study must be extended to a cohort with different gen-

der, age, etc. in different physical situations. Second,

the signal recording devices were chosen because of

availability rather than optimum superior signal qual-

ity. It is anticipated that better results could be ob-

tained by using an ECG device with a higher sampling

rate and full control of the ampliﬁcation and ﬁlter-

ing of the signal. In particular, the asymmetry of the

T wave is suspiciously absent on our data generated

with the Zephyr Bioharness. Likewise, no informa-

tion from the P wave has been included.

Similarly, a more precise respiration sensor with

higher sampling rate and larger immunity to move-

ment artifacts would provide higher quality data to

feed into the evolutionary algorithm.

The goal of this work has been to investigate the

feasibility of optimizing EDR with an evolutionary

algorithm and provide a proof of concept. More re-

search remains to be done, but we have found that it is

indeed possible to optimize EDR with an evolutionary

algorithm and we believe that evolutionary algorithms

will provide a fruitful tool for further studies in EDR

and other biomedical signal processing problems.

ACKNOWLEDGEMENTS

This work is a part of the MIKAT project funded

by Region Midtjylland and the European Union via

Caretech Innovation.

REFERENCES

Clifford, G. D., Azuaje, F., and McSharry, P. E., editors

(2006a). Advanced methods and tools for ECG data

analysis. Artech House Publishing.

Clifford, G. D., Azuaje, F., and McSharry, P. E., edi-

tors (2006b). Advanced methods and tools for ECG

data analysis. Artech House Publishing, accompa-

nying website. Retrieved june 23, 2011 from http://

www.ecgtools.org.

Dobrev, D. and Daskolov, I. (1998). Two-electrode telemet-

ric instrument for infant heart rate and apnea monitor-

ing. Medical Engineering & Physics, 20:729–734.

Grossman, P. and Wientjes, K. (1986). Respiratory sinus

arrhytmia and parasympathetic cardiac control: some

basic issues concerning quantiﬁcation, applications

and implications. In Grossman, P., Jansenn, K., and

Waitl, D., editors, Cardiorespiratory and cardioso-

matic psycophysiology, pages 117–138. Plenum Press,

NY.

Koza, J. R. (1992). Genetic Programming: On the Pro-

gramming of Computers by Means of Natural Selec-

tion. MIT Press, Cambridge, MA, USA.

MATLAB (2010). version 7.11.0.584 (R2010b). The Math-

Works Inc., Natick, Massachusetts.

Mazzanti, B., Lamberti, C., and de Bie, J. (2003). Val-

idation of an ECG-derived respiration monitoring

method. Computers in Cardiology, 30:613–616.

Moody, G., Mark, R., Zoccola, A., and Mantero, S.

(1985). Derivation of respiratory signals from multi-

lead ECGs. Computers in Cardiology, 12:113–116.

O’Brien, C. and Heneghan, C. (2007). A comparison of

algorithms for estimation of a respiratory signal from

the surface electrocardiogram. Computers in Biology

and Medicine, 37:305–314.

Raymond, B., Cayton, R. M., Bates, R. A., and Chappell,

M. J. (2000). Screening for obstructive sleep apnoea

based on the electrocardiogram - the computers in car-

diology challenge. Computers in Cardiology, 27:267–

270.

Schmidt, M. and Lipson, H. (2009). Distilling free-

form natural laws from experimental data. Science,

324(5923):81–85.

Sobron, A., Romero, I., and Lopetegi, T. (2010). Evaluation

of methods for estimation of respiratory frequency

from the ECG. Computers in Cardiology, 37:513–

516.

Zephyr Bioharness (n.d.). Retrieved june 23, 2011, from.

http://www.zephyr-technology.com.

BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing

152