
SIMULATING PEDESTRIAN ROUTE SELECTION WITH
IMPERFECT KNOWLEDGE
Kyle Feuz and Vicki Allan
Department of Computer Science, Utah State University, Logan, U.S.A.
Keywords:
Multi-agent systems, Pedestrian simulation, Heuristic route selection, Emergency egress.
Abstract:
Heuristic evaluation of possible route choices allows pedestrians to make decisions in a timely and efficient
manner. The heuristic function used to evaluate the route and the subsequent route selection has a large impact
on the egress time of the pedestrian. We implement several common heuristic functions using the PLEASE
simulation model and allow these heuristics to be combined using weighted factors. When the total distance
of a route is unknown, using a greedy strategy of selecting the shortest-leg first route is shown to be a poor
choice. When combined with other heuristic estimates however, including shortest-leg first costs can help to
decrease egress times. We show that for a variety of building layouts using a heuristic function based upon
width, distance, signage and congestion levels leads to better egress times.
1 INTRODUCTION
In everyday life, pedestrians frequently utilize heuris-
tics to make potentially complicated decisions within
an allotted time frame. These heuristics often allow a
person to make a reasonable decision without requir-
ing extensive amounts of time and energy. One ex-
ample arises from the evacuation of a burning build-
ing. Selecting the best route can mean the difference
between life and death, but frequently insufficient in-
formation is used in making this decision. Currently,
detailed information about pedestrian egress from ac-
tual emergencies is not widely available, and thus it
is too costly, too dangerous, and impractical to de-
termine what heuristics pedestrians use to select an
egress route when in emergency situations. Pedestrian
simulation models have been designed to address this
problem.
Current pedestrian simulation models generally
fall into one of two categories when determining
pedestrian route selection. Either the model assumes
pedestrians have perfect knowledge of the building
layout and are thus able to select the best route, or the
model assumes that pedestrians only know about the
immediately visible routes and must make a decision
based upon some heuristic (Pan, 2006; Thompson and
Marchant, 1995; Gwynne et al., 2001). Models which
assume perfect knowledge are clearly unrealistic for
many situations as not all pedestrians will be famil-
iar with any given building layout. Yet models re-
lying upon a heuristic may also be unrealistic in the
amount of information provided to pedestrians. Typi-
cally such heuristic models consider distance, conges-
tion or social comparison for making the route selec-
tion decision. In this paper, we show that using dis-
tance as the sole means of comparing visible routes
leads to poor egress times when the total route dis-
tances are unknown and is actually equivalent to the
shortest-leg first heuristic which Golledge found in
(Golledge, 1995) to be less preferred than many other
heuristics. Therefore, if total route distances are as-
sumed to be unknown to the pedestrians, then other
route selection heuristics must be used to supplant the
unknown information.
In this paper, we consider the effect of various
heuristic functions on pedestrian egress time for a
variety of different building layouts. Determining
a comprehensive list of heuristic functions, which
pedestrians might use, is outside of the scope of this
paper. However, several common factors including
distance, signage, corridor width, congestion/usage,
and common consensus are used to produce a variety
of realistic heuristic functions.
2 RELATED WORK
In (Ozel, 2001), Ozel raises several pertinent ques-
tions regarding the issue of stress management and the
decision process. He suggests that pedestrians utilize
146
Feuz K. and Allan V..
SIMULATING PEDESTRIAN ROUTE SELECTION WITH IMPERFECT KNOWLEDGE.
DOI: 10.5220/0003726201460153
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 146-153
ISBN: 978-989-8425-96-6
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
various coping mechanisms (heuristics) to make a de-
cision in a time-pressured environment. In particular,
the familiarity of routes and the negative connotations
of emergency exits are shown to have a large impact
on the route choice of pedestrians in an emergency.
Hoogendoorn and Bovy use distance and con-
gestion heuristics for their route-choice and activity
scheduling model (Hoogendoorn and Bovy, 2004).
Gwynne et. al. indicate that pedestrians maintain so-
cial roles and norms even during emergency situations
(Gwynne et al., 2006). This may lead to pedestri-
ans choosing a different route based on the choices of
their peers. Similarly, Fridman and Kaminka develop
a pedestrian simulation model based upon social com-
parison theory (Fridman and Kaminka, 2007).
Golledge ranks the preference and prevalence of
several different heuristic values pedestrians use in
navigation and route selection in an outdoor environ-
ment such as a college campus through the use of
questionares and observations (Golledge, 1995). He
finds that pedestrians prefer routes which are direct,
quick, and easy to navigate with some preference be-
ing given to routes which are more aesthetically pleas-
ing. In emergency situations, one would expect the
characteristics of directness and quickness to remain
prominent while the importance of scenery is irrele-
vant. Golledge also found that the route selection cri-
teria used differed for various route layouts and that
a combination of multiple criteria may give better re-
sults.
3 HEURISTICS
Our research evaluates a variety of heuristics. We de-
scribe several possible heuristics in the section.
Distance is a common heuristic used by pedestri-
ans when making a route selection and is the primary
heuristic in many search based strategies (Hoogen-
doorn and Bovy, 2004). Unless motivated by other
factors, pedestrians will choose the route which has
the shortest distance (Golledge, 1995). The dis-
tance heuristic is inapplicable in the absence of com-
plete route distance knowledge because missing data
causes the distance relation to be a partial order.
The shortest-leg first heuristic is a greedy dis-
tance heuristic. Rather than utilizing the total route
distance, shortest-leg first selects the route with the
shortest distance to the next decision point. Pedes-
trians only require distances to route goals which are
within their field of view.
Another common heuristic used by pedestrians
when selecting a route is the least angle heuristic
(Dalton, 2003; Hochmair and Frank, 2000). This
heuristic selects the path which is closest in terms of
angularity to a direct line between their current po-
sition and the final goal (B
¨
uchner et al., 2007). For
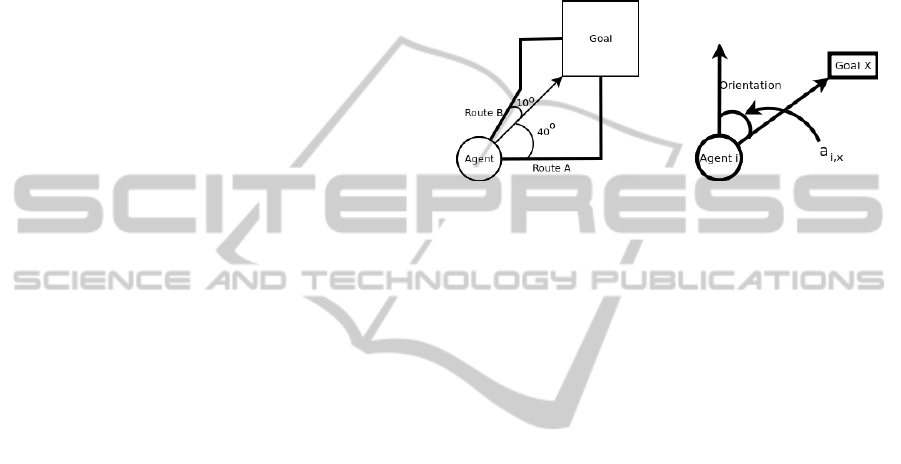
example, in Fig. 1 the agent would select Route B
when using the least angle heuristic because it is the
route whose angle differs the least from the angle to
the goal. Unfortunately, the end goal location(s) is
not always known. In such situations, the least-angle
heuristic cannot be applied.
(a) Example using the least-
angle heuristic
(b) Depicts the values used to
calculate the angle heuristic
Figure 1: Least-Angle heuristic examples.
We can modify the least angle heuristic to accom-
modate unknown goals by selecting the closest path in
terms of angularity to the current walking orientation.
This new heuristic is actually a greedy version of the
fewest turns heuristic as it tries to minimize the num-
ber of direction changes an agent makes while exiting
from the building.
Most buildings include navigational signs to assist
pedestrians in locating their desired location (Kray
et al., 2005). These signs might include exit signs,
emergency exits signs, room signs, or navigational
maps. Pedestrians then use these signs to navigate
effectively through the building. One might think that
during an emergency evacuation pedestrians would
look for exit signs or emergency exit signs, but Ozel
found that emergency exit signs often have negative
connotation and are avoided even in emergency situ-
ations (Ozel, 2001). Exit signs, on the other hand, are
commonly used by pedestrians in navigational plan-
ning when in an unfamiliar building. Room signs can
also be used in egress route planning as they indicate
that an egress route through a particular door is un-
likely because individual rooms rarely contain egress
routes.
Main corridors tend to be preferred by pedestri-
ans especially when navigating an unfamiliar building
(Hillier, 1996). Like the relative width of various cat-
egories of roads, main corridors are wider than aux-
iliary hallways so the width of the corridor or door-
way can frequently be an indication of a main route
of travel leading to an exit.
The number of pedestrians currently gathered
around a location may be either a positive or a nega-
SIMULATING PEDESTRIAN ROUTE SELECTION WITH IMPERFECT KNOWLEDGE
147

tive indicator of a desirable exit route (Gwynne et al.,
2006; Pan, 2006; Koh et al., 2008). It may indicate
the route is a good choice because others are using
it. However, it may also indicate that another route
should be considered to avoid the congestion. Intu-
ition suggests that if pedestrians are unsure about the
situation, they will follow others. If they are more
confident and know multiple routes, they will seek al-
ternatives to avoid congestion.
Unless the pedestrians are traveling in a group,
they will not know the exact route of nearby pedes-
trians. However, by observing the velocity and past
movement, an agent may predict the immediate des-
tination of a neighboring pedestrian. Seeing agents
who are traveling in the same direction may bolster
the confidence level of an agent in choosing a partic-
ular route (Ozel, 2001). Traveling in the same direc-
tion as others is also easier as one does not have to
fight against the general direction flow, improving the
overall pedestrian flow.
Pedestrians will typically choose routes with
which they are familiar especially when under time
constraints (Ozel, 2001). Familiarity allows the
pedestrian to feel more comfortable and confident in
the route selected and allows the pedestrian to con-
centrate on other cognitive tasks. However, select-
ing a new route may or may not lead to a better solu-
tion. When the current known route cost is within an
acceptable limit, pedestrians are unlikely to change.
The cost of a route may be based upon any number
of factors such as distance, congestion, time, and so
on. Readers may refer to (Feuz, 2011) for details of
including distance and congestion costs as learned by
past experience.
4 SIMULATION ENVIRONMENT
This study is performed using the Pedestrian Leader-
ship and Egress Assistance Simulation Environment
(PLEASE). PLEASE is built upon the multi-agent
modeling paradigm where each pedestrian is repre-
sented as an individually rational agent capable of
perceiving the environment and reacting to it. In
PLEASE, pedestrian agents can perceive obstacles,
hazards, routes, and other agents. The agents use a
two tier navigational module to control their move-
ment within the simulation environment. The high-
level tier evaluates available routes and selects a des-
tination goal. The low-level tier, based on the social
force model (Helbing and Johansson, 2009), performs
basic navigation and collision avoidance.
PLEASE implements several of the heuristics out-
lined in Section 3. Here we describe the implementa-
tion details used for the heuristics of interest. Many
simulation models assume that total route distance is
known and/or the end goal location is known for at
least some subset of the available routes. However,
in this paper, we are interested in the case when no
additional information, beyond what is immediately
visible to the pedestrian, is provided. For this reason,
the distance, angle and learned-costs heuristics are not
considered.
Each heuristic can potentially be combined with
any other heuristic. To facilitate the integration of
multiple heuristics, all heuristic values are normalized
so that the unweighted cost falls between 0 and 1.
The leg cost of route x, L(x), is given by Formula
1 where w
l
is the weight applied to the shortest-leg
heuristic, and d
i,x
is the distance from agent i to route
goal x. The distance is normalized using the maxi-
mum distance between two points on the simulation
map. Agents in the simulation are able to accurately
estimate the distance to visible points within the sim-
ulation model. The distance to locations which are
occluded by walls or other obstacles cannot be esti-
mated without prior knowledge.
L(x) =
w
l
∗ d
i,x
(maxDistance)
(1)
The turn cost of route x, T(x), is given by Formula
2, where w
t
is the weight applied to the fewest turns
heuristic, and a
i,x
is the angle in radians between the
orientation of agent i and the direction to route goal x
from agent i. π acts as the normalization factor since
no angle will be greater than π. See Figure 1 for an
example.
T (x) = w
t
∗ a
i,x
/π (2)
The signage cost of route x, S(x), is given by For-
mula 3, where w
s
is the weight applied to the signage
heuristic, and getExitWeight(x) is the cost associated
with the given signage value. getExitWeight takes the
signage of a route and looks up the user-specified cost
of that sign. A user may specify arbitrary sign costs,
but by default, PLEASE uses the costs shown in ta-
ble 1. To be consistent with the other heuristics, cost
should be specified as a value between 0 and 1.
S(x) = w
s
∗ getExitWeight(x) (3)
Table 1: Default parameters used in PLEASE.
Sign Type Cost Width Cost
Emergency Exit 0.25 Small 1.0
Exit 0.0 Medium 0.5
Room 1.0 Large 0.0
None 0.5
The simple signage cost of route x, SS(x), is given
by Formula 4, where w
ss
is the weight applied to the
ICAART 2012 - International Conference on Agents and Artificial Intelligence
148

simple signage heuristic, and getSimpleSignage(x) is
the cost associated with the simple signage of route x.
A route has a simple signage cost of 0 if the doorway
of the route is a direct exit and is marked with an exit
sign. All other routes have a simple signage cost of 1.
This causes a pedestrian to ignore all building signage
except for exit signs over direct exits. The simple sig-
nage heuristic allows us to compare the effect that dif-
ferent amounts of building signage and different lev-
els of attention to the building signage have upon the
egress times of pedestrians.
SS(x) = w
ss
∗ getSimpleSignage(x) (4)
The width cost of route x, W (x), is given by For-
mula 5, where w
w
is the weight applied to the corri-
dor width heuristic, and getCorridorWeight(x) is the
cost assigned to the given corridor width. The getCor-
ridorWeight is a lookup table which takes the width
of a route and returns the user-specified cost for that
width. A user may enter any arbitrary width cost, but
by default, PLEASE uses the costs shown in table 1.
To be consistent with the other heuristics, cost should
be specified as a value between 0 and 1. Although
corridor width is a real number and can have an in-
finite number of values, the getCorridorWeight dis-
cretizes width into three categories, small, medium
and large. This is done to eliminate meaningless dif-
ferences between corridors. Two corridors which dif-
fer only slightly in width are equally likely to indicate
a main route and should be treated equally. The cut-
off values for these categories can be set by the user so
that the values are appropriate for the current building
layout. By default, PLEASE uses 1.5 m and 2.5 m as
the cutoff values. Agents in the simulation measure
width at the entry point of the corridor.
W (x) = w
w
∗ getCorridorWeight(x) (5)
The congestion cost of route x, Cong(x), is given
by Formula 6, where w
cg
is the weight applied to
the congestion heuristic, sp
i
is the desired speed (a
normally distributed parameter value unique to each
pedestrian) of pedestrian i, sp
j
is the speed of pedes-
trian j, s
1
is 1 if sp
j
< sp
i
or 0 otherwise, n
p,x
is the
number of pedestrians along route x, and n
p
is the to-
tal number of pedestrians. This formula assigns cost
based upon the desired speed of the pedestrian and the
current speed of pedestrians along the selected route.
For each pedestrian along the selected route, if their
speed is slower than the desired speed, then a cost is
incurred relative to the speed difference. The cost is
raised to the square so that smaller speed differences
count less than larger differences. Finally, the result is
normalized by the worst case cost (i.e. if every pedes-
trian in the simulation was along the selected route
and was not moving).
Cong(x) = w
cg
∗
n
p,x
∑
j=0
((sp
i
− sp
j
) ∗ s
1
)
2
sp
i
∗ n
p
(6)
The consensus cost of route x, C(x), is given by
Formula 7, where w
c
is the weight applied to the con-
sensus heuristic, a
j,x
is the angle between pedestrian
j’s orientation and the direction to route goal x from
agent j (see Figure1), and n
p,i
is the number of pedes-
trians surrounding pedestrian i.
C(x) = w
c
∗
n
p,i
∑
j=0
(a
j,x
/π)
n
p,i
(7)
The previously visited cost of x, V (x), is given
by Formula 8, where w
v
is the weight applied to the
visited heuristic, and visitedCount(x) is the number
of remembered times route x has been visited by the
pedestrian in this simulation run. Each pedestrian is
capable of remembering a specified limit of number
of routes for a specified amount of time to reflect the
finite memory of pedestrians. These limits may be
set to any arbitrary value by the user, but by default,
PLEASE has a limit of 10 routes for 1000 seconds.
V (x) = w
v
∗ visitedCount(x)/maxMemory (8)
5 EXPERIMENTAL DESIGN
To test the effectiveness of the various heuristics de-
scribed above, we use a combination of actual build-
ing layouts and building layouts constructed for the
purpose of these experiments. In the buildings shown
in Figure 2, blue lines represent walls of the build-
ings, dashed green lines represent exits signs, solid
red lines represent emergency exit signs, and wavy
gold lines represent door signs. The USU Business
building (see Figure 2(a)) is an approximation of the
ground floor of the actual building found on the Utah
State University Campus. Likewise, the CSULB FM
building (see Figure 2(c)) and the CSULB UP build-
ing (see Figure 2(b)) are approximations of the ac-
tual buildings found on the California State Univer-
sity, Long Beach campus.
The USU Business building and the CSULB UP
building are used because the floor plans follow ex-
pected conventions: rooms do not function as hall-
ways, main areas have wide corridors, and other ac-
cepted conventions are followed. The CSULB FM
building is used because of the lack of convention
with room placement. Rooms are found within rooms
and several rooms can even function as hallways. The
custom building is designed to represent a standard
SIMULATING PEDESTRIAN ROUTE SELECTION WITH IMPERFECT KNOWLEDGE
149

(a) USU Business Building Floor 1 (b) CSULB UP
Building
(c) CSULB FM Building (d) Custom Building
Figure 2: Building layouts used in the heuristic evaluation experiments.
building. The corridor widths are not an exact indi-
cation of main routes and areas, but are still closely
correlated to main routes. Rooms do not function as
hallways. The number of rooms and routes are not so
many as to be completely unmanageable by pedestri-
ans either.
For each building, we conduct a variety of tests.
We measure the total egress time of 100 pedestrians,
randomly distributed throughout the rooms, averaged
over 20 simulations using a single active heuristic. In
all the tests, the previously visited heuristic is always
active and is given a weight of five. This represents
the agents’ unwillingness to backtrack along a route
previously traveled.
The viability of the signage heuristic is completely
dependent upon the type and amount of signage found
with the buildings. For this reason, a comparison be-
tween the signage and simple signage heuristics is
helpful. The simple signage heuristic represents the
same building stripped of all signs except for exit
signs at actual exit doorways.
Based upon the performance of the individ-
ual heuristics, we then combine multiple heuristics,
weighting each heuristic by its relative performance
in relation to the total egress time achieved by the
heuristics. These weights are then adjusted to further
improve the performance of the combined heuristics.
Determining the exact weight specification to opti-
mize performance when multiple heuristics are used
is outside of the scope of this paper.
6 RESULTS AND ANALYSIS
In this section, we discuss the results of the exper-
iment in four parts. First, we look at the effect of
building layouts on egress times. Second, we consider
in detail the result of applying only one heuristic at a
time. Third, we look at the results of applying mul-
tiple heuristics simultaneously. Fourth, we rank each
heuristic using a relative performance ratio.
6.1 Building Layouts
The USU Business building and the CSULB-UP
building have similar results for several of the heuris-
tics (see Figure 3). This makes sense because both
buildings have similar design characteristics. The
main differences in heuristic performance occurred
with the shortest-leg heuristic. The USU Business
building layout happens to be conducive to using the
shortest-leg heuristic. The outside rooms can actually
be used as hallways which lead directly to the exits,
and this is exactly what happens when the shortest-
leg heuristic is used. The ground floor of the USU
Business building layout appears similar to the cus-
tom building layout, yet the slight differences in spac-
ing and room layout create large differences in egress
times for the two buildings.
0
2
4
6
8
10
12
14
shortestLeg
signage
simpleSignage
width
congestion
random
Relative Performance Ratio
Heuristic Function
Effect of Building on Heuristic Performance
Custom
USU Business
CSULB FM
CSULB UP
Figure 3: Effect of building layout on heuristic effective-
ness. Performance ratio is calculated as the average time
taken for 90% of the pedestrians to evacuate using the given
heuristic divided by the average time taken for 90% of the
pedestrians to evacuate using perfect knowledge.
The CSULB FM building and the custom build-
ing both have similar results in egress times for the
shortest-leg, signage, congestion and random heuris-
tics. Although the actual layouts of the building are
quite different, the underlying patterns are similar:
ICAART 2012 - International Conference on Agents and Artificial Intelligence
150

width correlates with egress routes, long hallways
have many adjoining rooms, and exits are distributed
in a uniform manner. The main difference between
the results for each building is the performance of the
width heuristic. In the CSULB FM building, corridor
width corresponds closely with egress routes, while
in the custom building the correlation is weaker. The
simple signage heuristic also yields different results
in these two buildings. In the custom building, the
top left and top right exits are not visible throughout
most of the building and are thus highly underutilized.
Meanwhile, the exits in the CSULB FM building have
a much higher level of visibility throughout the build-
ing and are used more effectively.
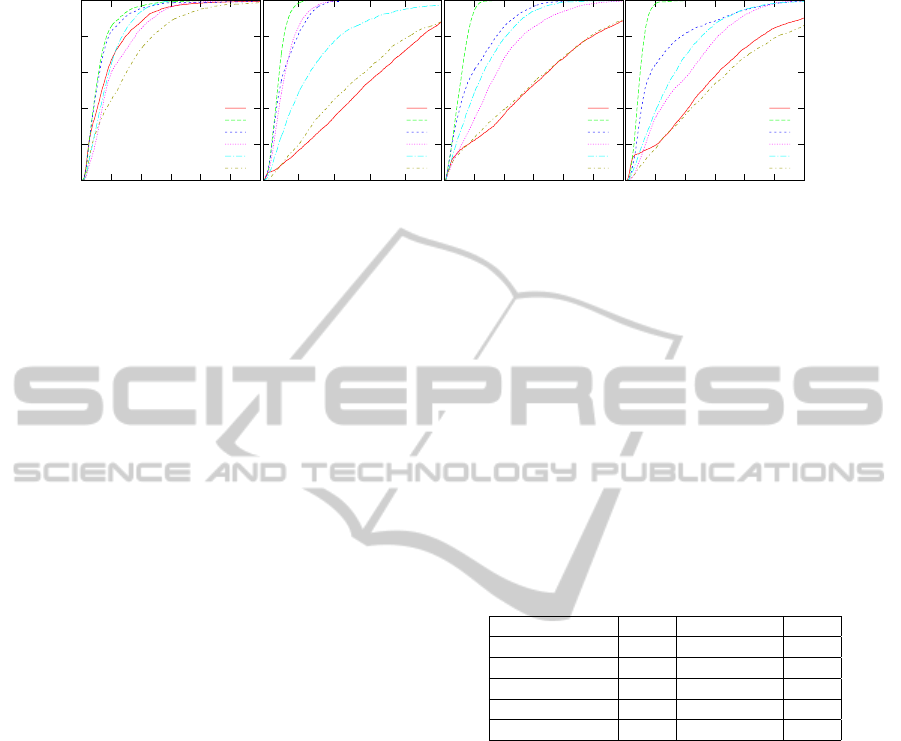
6.2 One Heuristic
When only a single heuristic is used, the results vary
greatly between heuristics (see Figure 4). The signage
heuristic performs well in all types of building lay-
outs tested. This suggests that if pedestrians choose
an egress route based upon well-designed signage,
pedestrians can efficiently egress from a building even
when completely unfamiliar with the layout of the
building. Using simple signage, the egress times are
still as good as or better than any other heuristic in
the building layouts considered. This highlights the
importance of even minimal building signage in as-
sisting in pedestrian egress.
The shortest-leg heuristic leads to slow egress
times in almost every building layout considered. In
many instances, the shortest-leg heuristic does not
even outperform a random choice policy. As dis-
cussed in Section 3, when the end goal is not known,
choosing the route which is closest to the pedestrian
becomes the shortest-leg first heuristic. This greedy
route selection heuristic provides no guarantee that
the route chosen will even lead to a direct exit. Ad-
ditionally, when distance is the sole means of eval-
uating a route, congestion is a common occurrence.
Pedestrians who are closest to a given doorway will
select that doorway regardless of what side they are
on or which direction other pedestrians are moving.
Thus, the pedestrians on opposite sides of the door-
way will converge at the doorway causing a bottle-
neck, and pedestrian flow rates through the doorway
will be greatly inhibited. Interestingly, the shortest-
leg heuristic performs remarkably well in the USU
Business Building (see Figure 4). This building is
configured ideally so that greedily selecting the clos-
est visible route actually leads pedestrians to an exit
in a fairly efficient manner. One reason that this is the
case is the double doors on most of the rooms. This
allows the pedestrian to explore routes without having
to backtrack, which is discouraged by the algorithm.
Additionally, the end rooms have doorways adjacent
to exits, which facilitates egress in this situation.
Similar to the shortest-leg heuristic, the fewest
turns heuristic also leads to poor performance. The
results are not shown here. The intuition behind the
fewest turns heuristic is to select a route that is as di-
rect as possible. However, considering only the next
route goal is too short-sighted and leads to routes
which are drastically less direct than they could be.
Without prior knowledge about the building layout,
though, this short-sightedness cannot be overcome.
For the building layouts considered in this paper,
the width heuristic leads to average egress times when
compared to the other heuristics. For the CSULB-FM
building, choosing the widest route leads to finding an
exit sooner than selecting a route by any other heuris-
tic except for signage. In the remaining buildings, the
width heuristic performs worse than the congestion
heuristic, but still significantly outperforms a random
policy.
The congestion heuristic does not necessarily pro-
vide an indication of which route leads to an exit,
especially when none of the pedestrians have any
knowledge regarding the building layout. However,
avoiding congestion still improves the overall egress
time by helping prevent bottlenecks and increasing
the overall smoothness of pedestrian flow. This al-
lows more routes to be explored in less time, which
leads to better egress times. Although (due to space
limitations) the results are not shown here, the con-
sensus heuristic also relieves congestions at bottle-
necks and improves pedestrian flow so that routes
can be explored in a more efficient manner. To be
most effective, the congestion and consensus heuris-
tics should be combined with another heuristic such
as width or signage which provide an indication of an
egress route.
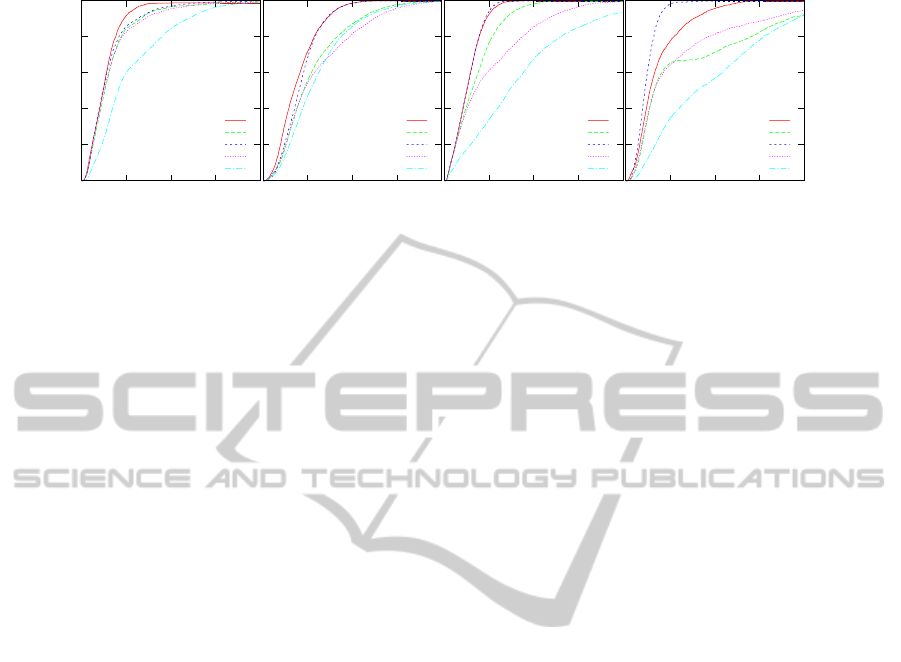
6.3 Multiple Heuristics
After considering each heuristic individually, we then
combine several heuristics to further improve perfor-
mance (see Figure 5). Although many different com-
binations could be tried, in this paper, we consider
combining the simple signage and width heuristics
(SS-W) and the shortest-leg, simple signage, width,
and congestion (SL-SS-W-C) heuristics. When width
is the sole heuristic applied, the egress times are too
slow to be reliable in an emergency. The simple sig-
nage heuristic is also slower than desired but is still
the best alternative to the signage heuristic (which
may not be realistic for many buildings) when only
a single heuristic is applied. The goal of combining
SIMULATING PEDESTRIAN ROUTE SELECTION WITH IMPERFECT KNOWLEDGE
151
0
0.2
0.4
0.6
0.8
1
0 50 100 150 200 250 300
Percent Evacuated
Time (seconds)
Business Building
100 200 300 400 500
Time (seconds)
CSULB-FM Building
50 100 150 200 250 300
Time (seconds)
CSULB-UP Building
50 100 150 200 250 300
Time (seconds)
Custom Building
shortestLeg
signage
simpleSignage
width
congestion
random
shortestLeg
signage
simpleSignage
width
congestion
random
shortestLeg
signage
simpleSignage
width
congestion
random
shortestLeg
signage
simpleSignage
width
congestion
random
Figure 4: Agent egress times using multiple heuristics in the Simple building.
width and simple signage is to take advantage of the
signage when available and to fall back on the width
heuristic when the signage is not available . We then
include the other heuristics, namely shortest-leg and
congestion, to further improve the egress times. For
comparison purposes, the egress times of the signage,
simple signage and width heuristics are included in
the charts.
As can be seen in Figure 5, combining the sim-
ple signage and width heuristic (SS-W) did indeed
improve performance in most buildings in compari-
sion to either heuristic alone. The custom building
layout is the one exception. In this building, falling
back on width proved to be detrimental to the over-
all egress time as the widest areas did not have di-
rect exits. However, when several heuristics (shortest-
leg, simple signage, width and congestion, denoted
as SL-SS-W-C) are combined, performance is im-
proved in every single building layout when com-
pared to the performance of the heuristics separately.
In most cases, the egress times matched or beat select-
ing routes based upon perfect signage. This indicates,
that for a wide variety of buildings, the same heuristic
functions can be applied to successfully egress from
the building in a reasonably efficient manner using
only the information which is directly perceivable by
the pedestrian.
Although the shortest-leg heuristic did not per-
form well by itself, when combined with other heuris-
tics, it leads to improved performance (results omit-
ted due to space limitations). This is indicative of the
value distance can play in route selection and justifies
its use by actual pedestrians. However, it is important
to note the disastrous impact which relying only upon
distance can have upon the total egress time of indi-
vidual pedestrians when no additional information is
utilized.
6.4 Heuristic Rankings
The heuristic functions are ranked according to the
relative performance ratio (RPR) of each heuristic in
the above mentioned building layouts. For each build-
ing, the average time (t) it takes for 90% of the pedes-
trians to evacuate when each pedestrian has perfect
knowledge of route distances and congestion levels is
recorded. The average time (h) it takes for 90% of the
pedestrians to evacuate when each pedestrian is us-
ing the heuristic function of interest is also recorded.
The RPR of each heuristic function is then computed
as h/t. Table 2 displays the average relative perfor-
mance ratio for each heuristic.
Table 2: Ranking of heuristic functions by relative perfor-
mance ratio (RPR). A lower RPR signifies better egress
times.
Heuristic RPR Heuristic RPR
signage 1.44 congestion 4.30
S-SS-W-C 1.59 consensus 4.65
SS-W 2.71 random 7.60
simpleSignage 2.89 shortestLeg 8.19
width 3.62 angle 9.41
7 CONCLUSIONS
Using heuristic estimations in selecting an egress
route is a natural and common process performed by
pedestrians on a daily basis, yet most simulation mod-
els do not adequately address this fact. This paper
highlights the importance of including heuristic costs
in pedestrian simulators, especially those designed to
model egress in an emergency situation. As Ozel indi-
cates in (Ozel, 2001), when in stressful situations and
under time constraints, pedestrians will react by filter-
ing and bolstering information (i.e. relying more upon
heuristic estimations). This leads to decisions which
are sub-optimal and, as shown, can have a significant
impact on the total egress time of the simulation. In
emergency simulation models, it is not sufficient to
assume pedestrians will make the best or even good
choices, the simulation model needs to consider the
ICAART 2012 - International Conference on Agents and Artificial Intelligence
152
0
0.2
0.4
0.6
0.8
1
0 50 100 150 200
Percent Evacuated
Time (seconds)
Business Building
50 100 150 200
Time (seconds)
CSULB-FM Building
50 100 150 200
Time (seconds)
CSULB-UP Building
50 100 150 200
Time (seconds)
Custom Building
SL-SS-W-C
SS-W
signage
simpleSignage
width
SL-SS-W-C
SS-W
signage
simpleSignage
width
SL-SS-W-C
SS-W
signage
simpleSignage
width
SL-SS-W-C
SS-W
signage
simpleSignage
width
Figure 5: Agent egress times using multiple heuristics in the Simple building.
possibility that pedestrians are forced to make split-
second decisions with little information.
When the total distance is unknown, using a
greedy strategy of selecting the closest route available
is seen to produce poor results in many circumstances.
If additional factors are included in the decision, then
the distance heuristic can help improve egress times,
even when the total distance is not known. Using four
main heuristics (the shortest-leg heuristic, the simple
signage heuristic, the width heuristic and the conges-
tion heuristic, each appropriately weighted) is shown
to produce good egress times even when no informa-
tion about the building layout is known before the
simulation begins. If only a single heuristic is used,
the signage heuristic gives the best results even when
the amount of building signage is minimal.
REFERENCES
B
¨
uchner, S., H
¨
olscher, C., and Strube, G. (2007). Path
choice heuristics for navigation related to mental rep-
resentations of a building. In Proceedings of the Euro-
pean Cognitive Science Conference, pages 504–509.
Taylor & Francis.
Dalton, R. (2003). The secret is to follow your nose. Envi-
ronment and Behavior, 35(1):107.
Feuz, K. (2011). Pedestrian leadership and egress assistance
simulation environment. Master’s thesis, Utah State
University.
Fridman, N. and Kaminka, G. (2007). Towards a cogni-
tive model of crowd behavior based on social compar-
ison theory. In Proceedings of the National Confer-
ence on Artificial Intelligence, volume 22, page 731.
Menlo Park, CA; Cambridge, MA; London; AAAI
Press; MIT Press; 1999.
Golledge, R. (1995). Path selection and route preference
in human navigation: A progress report. Spatial In-
formation Theory A Theoretical Basis for GIS, pages
207–222.
Gwynne, S., Galea, E., and Lawrence, P. (2006). The intro-
duction of social adaptation within evacuation mod-
elling. Fire and materials, 30(4):285–309.
Gwynne, S., Galea, E. R., Lawrence, P. J., and Filippidis, L.
(2001). Modelling occupant interaction with fire con-
ditions using the buildingexodus evacuation model.
Fire Safety Journal, 36(4):327–357.
Helbing, D. and Johansson, A. (2009). Pedestrian,
crowd and evacuation dynamics. In Encyclopedia of
Complexity and Systems Science, pages 6476–6495.
Springer.
Hillier, B. (1996). Space is the Machine. Cambridge Uni-
versity Press, Cambridge.
Hochmair, H. and Frank, A. (2000). Influence of estima-
tion errors on wayfinding-decisions in unknown street
networks–analyzing the least-angle strategy. Spatial
Cognition and Computation, 2(4):283–313.
Hoogendoorn, S. and Bovy, P. (2004). Pedestrian route-
choice and activity scheduling theory and models.
Transportation Research Part B: Methodological,
38(2):169–190.
Koh, W. L., Lin, L., and Zhou, S. (2008). Modelling and
simulation of pedestrian behaviours. In PADS ’08:
Proceedings of the 22nd Workshop on Principles of
Advanced and Distributed Simulation, pages 43–50,
Washington, DC, USA. IEEE Computer Society.
Kray, C., Kortuem, G., and Kr
¨
uger, A. (2005). Adaptive
navigation support with public displays. In Proceed-
ings of the 10th international conference on Intelligent
user interfaces, IUI ’05, pages 326–328, New York,
NY, USA. ACM.
Ozel, F. (2001). Time pressure and stress as a factor during
emergency egress. Safety Science, 38(2):95–107.
Pan, X. (2006). Computational Modeling of Human and
Social Behaviors for Emergency Egress Analysis. PhD
thesis, Stanford University, Stanford, California.
Thompson, P. and Marchant, E. (1995). Testing and ap-
plication of the computer model simulex. Fire Safety
Journal, 24(2):149–166.
SIMULATING PEDESTRIAN ROUTE SELECTION WITH IMPERFECT KNOWLEDGE
153
