
GRAPH RECOGNITION BY SERIATION AND FREQUENT
SUBSTRUCTURES MINING
Lorenzo Livi, Guido Del Vescovo and Antonello Rizzi
Department of Information Engineering, Electronics and Telecommunications,
SAPIENZA University, Via Eudossiana 18, 00184 Rome, Italy
Keywords:
Inexact graph matching, Graph seriation, Frequent substructures mining, Embedding, Granular computing,
Classification.
Abstract:
Many interesting applications of Pattern Recognition techniques can take advantage in dealing with labeled
graphs as input patterns. To this aim the most important issue is the definition of a dissimilarity measure
between graphs. In this paper we propose a representation technique able to characterize the input graphs
as real valued feature vectors, allowing the use of standard classification systems. This procedure consists
in two distinct stages. In the first step a labeled graph is transformed into a sequence of its vertices, ordered
according to a given criterion. In a second step this sequence is mapped into a real valued vector. To perform
the latter stage, we propose a novel Granular Computing procedure searching for frequent substructures, called
GRADIS. This algorithm is in charge of the inexact substructures identification and of the embedding of
the sequenced graphs using the symbolic histogram approach. Tests have been performed by synthetically
generating a set of graph classification problem instances with the aim to measure system performances when
dealing with different types of graphs, as well when increasing problem hardness.
1 INTRODUCTION
Many Pattern Recognition problems have been for-
mulated using labeled graphs as patterns. Despite
their relative simplicity and intuitive understanding,
their analysis imposes a new type of approach to stan-
dard Pattern Recognition techniques, such as clas-
sification and clustering. For this purpose, the re-
search field related to Pattern Recognition systems
able to deal with structured patterns is growing fast.
A key context in this scenario is the one of the In-
exact Graph Matching measures, aiming to establish
a (dis)similarity measure between graphs. Different
graph mining issues, such as for example Frequent
Subgraphs Mining (Kuramochi and Karypis, 2002),
are of great interest considering both their isolated
application, and in conjunction with more complex
modeling systems. For example the extrapolation of
a set of significative prototypes (Riesen and Bunke,
2010) of a given input dataset, permits to establish
what is called a relative reference framework, tailored
to the specific problem at hand.
Our intuition is that this set of prototypes, starting
from an input set of graphs, can be determined trans-
forming the original domain of the problem. Follow-
ing this approach, we have developed a representa-
tion technique, able to characterize the input graphs
as real valued feature vectors. Once the vector-
representation of the graphs is obtained, the inexact
graph matching between two graphs can be issued us-
ing any inductive modeling system relying on stan-
dard tools, fully taking advantage of the algebraic
structure usually adopted in R
n
.
In Section 2 the scientific context is introduced.
In Section 3 the proposed methodology is described.
The experimental evaluation of the proposed method-
ology is described in Section 4. Finally in Section 5
we draw our conclusions.
1.1 Preliminary Definitions
In this section we will give some basic preliminary
definitions, mainly regarding (labeled) graphs. A la-
beled graph is a tuple G = (V,E,µ,ν) , where V is
the (finite) set of vertices (also referred as nodes),
E ⊆ V ×V is the set of edges, µ : V → L
V
is the vertex
labeling function, with L
V
the vertex-labels set and
ν : E → L
E
is the edge labeling function, with L
E
the
edge-labels set. If L
V
= L
E
=
/
0 then G is referred
as an unlabeled graph. If L
E
= R
0
, then G is called
186
Livi L., Del Vescovo G. and Rizzi A. (2012).
GRAPH RECOGNITION BY SERIATION AND FREQUENT SUBSTRUCTURES MINING.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 186-191
DOI: 10.5220/0003733201860191
Copyright
c
SciTePress

weighted graph. If L
E
6=
/
0 ∧ L
V
=
/
0 the graph G is
referred as edge-labeled graph. If L
E
=
/
0 ∧ L
V
6=
/
0
the graph G is referred as vertex-labeled graph. Fi-
nally if both sets are non-empty we can refer to G
as a fully-labeled or simply labeled graph. The no-
tations V (G) and E(G) will refer to the set of ver-
tices and edges of the graph G. The cardinalities of
V (G) and E(G) are referred, respectively, as the or-
der and the size of the graph. The adjacency matrix
of G is denoted with A
n×n
, where |V (G)| = n, and if
G is weighted we have the weighted adjacency ma-
trix A
i j
= ν(e
i j
), sometimes denoted as W. The tran-
sition matrix is denoted with T
n×n
and is defined as
T = D
−1
A, where D is a diagonal matrix of vertices
degree, D
ii
= deg(v
i
) =
∑
j
A
i j
. If it is not explicitly
defined, in this paper a graph is assumed to be simple
and edge-labeled.
2 SCIENTIFIC CONTEXT
The recent research on inductive modeling has de-
fined many automatic systems able to deal with clas-
sification functions defined on R
n
. However, many of
the classification problems coming from practical ap-
plications deal with structured patterns, such as im-
ages, audio/video sequences and biological chemical
compounds. Usually, in order to take advantage of
the existing data driven modeling systems, each pat-
tern of a structured domain S is reduced to an R
m
vec-
tor by adopting a preprocessing function φ : S → R
m
.
The design of these functions is a challenging prob-
lem, mainly due to the semantic and informative gap
between S and R
m
. The key to design an auto-
matic system dealing with these classification prob-
lems is information granulation. Granular Comput-
ing (Bargiela and Pedrycz, 2003) is a novel paradigm
concerned with the analysis of complex data, usually
characterized by the need of different levels of rep-
resentation. Granular computing approach aims to
group low level information atomic elements into se-
mantically relevant structures. These groups of enti-
ties are called information granules. Granular mod-
eling consists in finding the correct level of informa-
tion granulation, i.e. a way to map a raw data level
domain into a higher semantic level, and in defining a
proper inductive inference directly into this symbolic
domain.
The graph matching problem is an important re-
search field characterized by both theoretical and
practical issues. The numerous matching procedures
proposed in the technical literature can be classified
into two well defined families, those of exact and in-
exact matching. The first one is just a boolean equal-
ity test given two input graphs, while the latter is
a more complex and interesting problem where the
challenge is in computing how much they differ. In
the current scientific literature it is possible to dis-
tinguish three mainstream approaches: Graph Edit
Distance based (Neuhaus et al., 2006; Riesen and
Bunke, 2009), Graph Kernels based (Borgwardt et al.,
2005; Vishwanathan et al., 2008) and Graph Embed-
ding based (Riesen and Bunke, 2010; Del Vescovo
and Rizzi, 2007).
3 GRAPH EMBEDDING METHOD
In this section we will explain the proposed method-
ology to solve the inexact graph matching problem.
The basic and intuitive idea is that if two given graphs
are similar, they should share many similar substruc-
tures. To be able to understand the similarity of the
two graphs in terms of their common substructures,
we first transform each graph into a sequence of its
vertices, and then we perform a recurrence analysis of
the inexact substructures of these sequenced graphs.
The proposed method is thus a two-stage algorithm,
where the first one is dominated by a graph seriation
procedure, and the last one by a sequence mining and
representation of the identified subsequences. The
proposed method can be represented as two mapping
functions. The first one, say f
1
: G → Σ, maps a graph
G ∈ G to a sequence of vertices identifiers s ∈ Σ. The
second one, say f
2
: Σ → E, maps each sequence s ∈ Σ
to a numeric vector h ∈ E, where usually E ⊆ R
n
.
Therefore, eventually, the problem is posed on a stan-
dard domain, such as for example an Euclidean space,
where the whole set of known Pattern Recognition
methods can be applied directly. Consequently, this
methodology should be seen as a mixture of Graph
Embedding and Graph Edit Distance approaches.
3.1 Graph Seriation
Given a graph G, the aim is to establish an order on the
set of vertices V (G), with |V (G)| = n, such that the
derived sequence of vertices s = (v
i
1
,v
i
2
,...,v
i
n
) re-
spects a given property of the graph. For example, an
interesting approach is the one that analyzes the spec-
trum (i.e. the set of its eigenvalues/eigenvectors) of
the matrix representation of the graph (Robles-Kelly
and Hancock, 2005). The leading eigenvector φ of
the adjacency matrix contains the information about
the structural connectivity of each vertex of the graph.
Similarly, analyzing the (symmetric) transition matrix
T
n×n
, it is possible to obtain information about the a
priori probability of a given vertex in a random walk
GRAPH RECOGNITION BY SERIATION AND FREQUENT SUBSTRUCTURES MINING
187

scenario. In general this approach can be used for un-
weighted and weighted graphs. However, we observe
that it is possible to extend this method also to the
graphs with real vectors as weights on the edges, tak-
ing into account the (Euclidean) norm W
i j
=k ν(e
i j
) k
of the vector, assuming that the highest is the norm,
the stronger is the relationship.
In this paper, we will make use of this seriation
method (Robles-Kelly and Hancock, 2005) for three
types of edge-labeled graphs: unweighted, weighted
with a scalar in [0,1] and with a vector in [0, 1]
n
. Note
that the vertices can be arbitrarily labeled, but they are
irrelevant in this particular phase.
3.2 Sequence Mining and Embedding
In order to represent a seriated graph as a real valued
vector, we propose a method called GRADIS (GRan-
ular Approach for DIscrete Sequences), aimed at per-
forming two crucial tasks: the inexact substructures
identification, called the alphabet of symbols, and
the embedding of the sequences using the symbolic
histogram approach (Del Vescovo and Rizzi, 2007).
With a little bit of formalism, the proposed methodol-
ogy, seen from an high level of abstraction, can be
characterized using a mapping function f : Σ → E
that maps each sequence to a numeric vector, with
E ⊆ R
n
. This way, the problem is mapped into the
Euclidean domain.
Given an input dataset of sequences (i.e. se-
quences of characters) S = {s
1
,...,s
q
}, generated
from a finite alphabet Ω, the first task is to iden-
tify a set A = {a
1
,...,a
d
} of symbols. These sym-
bols are pattern substructures that are recurrent in the
input dataset. The identification of this set is per-
formed using an inexact matching strategy in con-
junction with a clustering procedure. Given a lower
l and upper L limit for the length of the subse-
quences, a variable length n-gram analysis is per-
formed on each input sequence of the dataset. An
n-gram of a given sequence s is defined as a con-
tiguous subsequence of s of length n. For in-
stance, if an input sequence is s = (A,B,C,D), with
l = 2,L = 3, we obtain the set of n-grams N
s
=
{(A,B),(A,B,C),(B,C),(B,C, D),(C, D)}. The car-
dinality of this set is then |N
s
| =
∑
L
i=l
(n − i) + 1 =
O(n
2
), where L ≤ n = len(s) (len(s) is the number
of elements into the sequence s). However, normally
L n and thus |N
s
| ' c · n, where c > 1 is a constant
factor. If M is the maximum length of a sequence of
the input dataset S, the cardinality of the whole set of
n-grams N = {n
1
,...,n
|N |
} of S is upper bounded by
|N | ≤ |S| ·
∑
L
i=l
(M − i) + 1 ' |S| · c · M.
Since the cardinality of N can become large, it is
convenient to perform this analysis on a subset of N ,
say N
∗
. For this purpose, a probabilistic selection of
each n-gram can be performed. With a user-defined
probability p an n-gram is selected, conversely with
probability 1 − p it is not selected. So, given a set of
m n-grams and a selection probability p, the chosen n-
grams can be described by a Binomial distribution. In
fact the expected number of selected n-grams in N
∗
is |N | · p, with variance |N | · p · (1 − p).
The set N
∗
is subjected to a clustering procedure
based on the BSAS algorithm. The Levenshtein dis-
tance is used as the dissimilarity measure between n-
grams and clusters are represented by the MinSOD
(Minimum Sum Of Distances) element. The cluster-
ing procedure aims to identify a list of different par-
titions of N
∗
, say L = (P
1
,...,P
z
). In fact the out-
come of the BSAS algorithm is known to strongly de-
pend on a clustering parameter called Θ. The opti-
mal value of Θ is automatically determined using a
logarithmic search algorithm. The Θ search interval
(usually [0, 1]) is recursively split in halves, stopping
each time that two successive values of the parameter
yield the same partition. The recursive search stops
anyway when the distance between two successive Θ
values falls under a given threshold. Each partition
P
i
= {C
1
,...,C
u
i
},i = 1 → z, is composed by u
i
clus-
ters of n-grams. Successively, these clusters are sub-
jected to a validation analysis, that takes into account
the quality of the cluster. For this purpose, for each
cluster C
j
∈ P
i
a measure of cluster compactness cost
K(C
j
) and size cost S(C
j
) is evaluated. Starting from
these measures, the following convex combination is
defined as the total cluster cost
Γ(C
j
) = (1 − µ) · K(C
j
) + µ ·S(C
j
) (1)
where K(C
j
) =
1
n−1
∑
n−1
i=1
d(n
i
,n
SOD
C
j
), n
SOD
C
j
is the
MinSOD element of the cluster C
j
and d(·, ·) is the
Levensthein distance. The size cost is defined as
S(C
j
) = 1 −
|C
j
|
|N
∗
|
. If the cost Γ(C
j
) is lower than a
given threshold τ, the cluster is retained, conversely
is rejected. Each (accepted) cluster C
j
is modeled by
a representative element, that is an n-gram n
SOD
C
j
that
minimizes the sum of distances between all the other
elements in the cluster. This representative element,
say a
j
= n
SOD
C
j
, is considered as a symbol of the input
dataset and it is added to the alphabet A. At the end
of this clustering procedure, the alphabet A of the in-
put dataset is determined. Actually, each symbol a
j
is
defined as a triple (n
SOD
C
j
,K(C
j
) · ε, 1 − Γ(C
j
)), where
K(C
j
) · ε is a factor used in the subsequent embed-
ding phase (ε is again a user-defined tolerance) and
1 − Γ(C
j
) is the ranking score (quality value of the
cluster C
j
) of the symbol a
j
in the alphabet A. Our
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
188

analysis aims to aggregating as much as possible sim-
ilar subsequences of the input dataset. For this reason,
each selected cluster should be seen as an information
granule of n-grams.
The second stage of the procedure is aimed at pro-
ducing an explicit embedding of each input string s
i
into a relative dissimilarity space (Pe¸kalska and Duin,
2005). This is done by counting the number of (inex-
act) occurrences of each symbol a
j
∈ A into the input
string s
i
. If |A| = d, where d ≤
∑
z
i=1
u
i
is the num-
ber of selected clusters representatives, the embed-
ding space E is a d-dimensional dissimilarity space,
and each input sequence s
i
is represented as a numer-
ical vector h
i
. Therefore, the set of symbols A should
be seen as a set of prototypes, used to explicitly model
the input data. The inexact matching is again per-
formed using the Levensthein distance. The count-
ing of the number of occurrences of a
j
, extracted
from cluster C
j
, into s
i
is performed as follows. Let
ν = len(s
i
)·λ be the length tolerance adopted in order
to find matches in s
i
, where λ is a user-defined param-
eter in [0, 1]. The selected set of n-grams N
s
i
of s
i
, of
variable length l between len(s
i
)−ν ≤ l ≤ len(s
i
)+ν,
is extracted and the inexact matching is performed
against a
j
and each o ∈ N
s
i
. If the alignment cost
is lower or equal to K(C
j
) · Θ, the counting is incre-
mented by 1. The value K(C
j
) · Θ is used to automat-
ically enable a cluster-dependent thresholding mech-
anism. In fact, the more the cluster is compact, the
higher the matching score should be in order to asso-
ciate that particular n-gram with the particular clus-
ter. Conversely, if the cluster is not so compact (i.e.
a noisy cluster), a larger matching tolerance should
be used in order to recognize the occurrence. For in-
stance, a cluster of perfectly identical elements would
yield K(C
j
) = 0, requiring an exact matching to rec-
ognize the occurrence of the symbol.
GRADIS should be seen as a data driven model-
ing system aimed at producing the alphabet of sym-
bols and an explicit representation model of the given
input dataset S. This model can be used in differ-
ent Pattern Recognition problems, such as for exam-
ple the ones of classification and clustering. In sum-
mary, in order to perform GRADIS on an input set
of graphs G = {G
1
,...,G
m
}, we firstly seriate each
graph G
i
producing a sequence of its vertices s
i
=
(v
i
0
,v
i
1
,...,v
i
n
). Then we apply the described proce-
dure to finally embed s
i
into the dissimilarity space
E, obtaining the symbolic histogram representation
h
i
. On the dissimilarity space (E,d(·,·)) any given
Pattern Recognition problem can be defined directly,
using any (metric) distance d : E ×E → R
+
0
. Usually,
the embedding space E is a large dimensional space,
and an automatic dimensionality reduction technique
using a feature selection scheme is normally a good
choice.
4 TESTS AND RESULTS
The performance tests are performed by facing clas-
sification problems using different synthetically gen-
erated datasets of graphs G. As we have said be-
fore, three kinds of edge-labeled graphs are taken
into account: unweighted, with a scalar weight in
[0,1] and weighted with a vector in [0,1]
n
, taking
n = 10. The general classification scheme is com-
posed by a training phase with a validation set (S
v
),
where feature selection is performed over the sym-
bolic histogram representation of the input patterns.
The subset of the features is selected optimizing a fit-
ness function using a genetic algorithm. If c ∈ {0,1}
d
,
with d = |A|, is the bit-mask of the features that bet-
ter performs on the validation set, and h is the sym-
bolic histogram representation of an input pattern, the
final synthesized model will be fed directly by the
reduced vector of features
ˆ
h = h⊥c. Note that the
symbol ⊥ means that we project the original vector h
into the subspace induced by selecting only the fea-
tures denoted by the bit-mask c. The fitness func-
tion adopted for the feature selection is defined as
f (
ˆ
h) = 1 − (αErr
S
v
+ (1 − α)FC), where FC stands
for the fraction of selected features using the bit-mask
c. It is a linear convex combination of the classifica-
tion error rate Err
S
v
on the validation set (as an esti-
mate of the generalization capability when selecting a
given feature subset
ˆ
h) and of a complexity measure
of
ˆ
h. The overall performance measure on the test set
(S
ts
) is defined as the complement of the classification
error rate Err
S
ts
, that is as f (
ˆ
h) = 1 − Err
S
ts
.
Software implementation is based on the C++
SPARE library (Del Vescovo et al., 2011). The tests
are executed on a machine with an Intel Core 2 Quad
CPU Q6600 2.40GHz and 4 Gb of RAM over a Linux
OS.
4.1 Problem Definition and Datasets
Each dataset of graphs G = {G
1
,G
2
,...,G
m
} is gener-
ated in a stochastic fashion based on Markov Chains.
Assuming to deal with graphs of the same order, that
is |V (G
i
)| = |V (G
j
)| = n,∀i, j, the Markov generation
process is entirely described by its transition matrix
T
n×n
. The size of each graph G is chosen with uni-
form probability in the range n − 1 ≤ |E(G)| ≤
n
2
.
Firstly, the n vertices of the graphs are generated, se-
lecting the first vertex of the random walk, say v
j
0
,
with uniform probability. Then, the i-th vertex in the
GRAPH RECOGNITION BY SERIATION AND FREQUENT SUBSTRUCTURES MINING
189

random walk, v
j
i
, is selected using the transition prob-
abilities of the given transition matrix T, that is with
probability T
j
i−1
, j
i
. During the random walk the edges
are created, together with the chosen labels that char-
acterize the type of graphs. This Markov graphs gen-
eration strategy will characterize the graphs with pe-
culiar walks, that are indeed the distinctive feature in
the recognition problem. In this way, we have con-
sidered two distinct stationary Markov chains that we
see as classes of graphs. Our classification problem
is then defined as a two class problem, where each
class is labeled with one of the two Markov chains.
Clearly the objective is to recognize graphs that were
generated from the same Markov chain.
4.2 Results for Different Graph Types
The first test is carried out over the three types of
graphs, and for each type the test is repeated five times
with different random seeds. This choice is motivated
by the fact that different parts of the proposed algo-
rithm are characterized by a random behavior, so we
need to estimate the overall performance measure re-
lying on different runs and computing the average and
variance of the results. For this purpose, we have
generated a random two-class set of datasets (in total
5 · 3 = 15 datasets), with 1000, 500 and 500 graphs,
of order 100, for the training, validation and test set,
respectively. As explained in Section 4.1, the size of
the graphs is randomly determined. The graphs are
equally distributed between the two classes. In Ta-
ble 1 are shown the classification results achieved us-
ing SVM and two training algorithms, namely ARC
and PARC (Rizzi et al., 2002), used to adopt a neuro-
fuzzy Min-Max model. We report the averaged clas-
sification accuracy and, in the column indexed with
the symbol σ, its standard deviation over the different
test sets. For what concerns both SVM and ARC, it is
possible to note a great accuracy in the classification
of these randomly generated graphs, with a low devia-
tion of the results. These tests show that the proposed
embedding procedure is effective when feeding even
very different classification systems, based on distinct
modeling strategies, as the considered ones.
4.3 Results with Increasing Difficulties
The aim of the second test is to progressively increase
the hardness of the test, reducing the differences be-
tween the transition matrices that generate the input
graphs G, that is, reducing the characteristic traits in-
side the generated graphs. For this test, we focus on
an equally distributed two-class classification prob-
lem only for weighted graphs. The order of the graphs
Table 1: Classification Accuracies Using SVM, ARC, PARC.
Algorithm Graph Type % Accuracy σ
SVM
Unweighted 100 0.0000
Weighted 97.92 0.2683
Vector-Weighted 98.64 0.3847
ARC
Unweighted 99.40 0.2607
Weighted 98.70 0.3551
Vector-Weighted 99.20 0.1525
PARC
Unweighted 96.08 1.6769
Weighted 95.56 1.3069
Vector-Weighted 96.12 0.6418
is 100 and, as usual, their size is randomly deter-
mined, with 1000, 500 and 500 graphs for the train-
ing, validation and test sets, respectively. To control
the hardness of the classification problem, we produce
a sequence of generating transition matrices with dif-
ferent level of randomness. A transition matrix is said
to be fully random if the transition probabilities are
uniform. Following this fact, for each classification
problem instance, we generate the two transition ma-
trices (one for each class of graphs) introducing two
real parameters, α,β ∈ [0,1], controlling the similarity
of the transition matrices. Let P
1
and P
2
be two dif-
ferent permutation matrices, and let U be the uniform
transition matrix, with a zero diagonal. We firstly gen-
erate two intermediate matrices, say A and B as fol-
lows
A = αU +(1 − α)P
1
(2)
B = αU +(1 − α)P
2
Finally we obtain the two transition matrices,
characterized by a desired similarity, as follows
T
1
= (β/2)A + (1 − (β/2))B (3)
T
2
= (β/2)B + (1 − (β/2))A
In the following tests different combinations of α
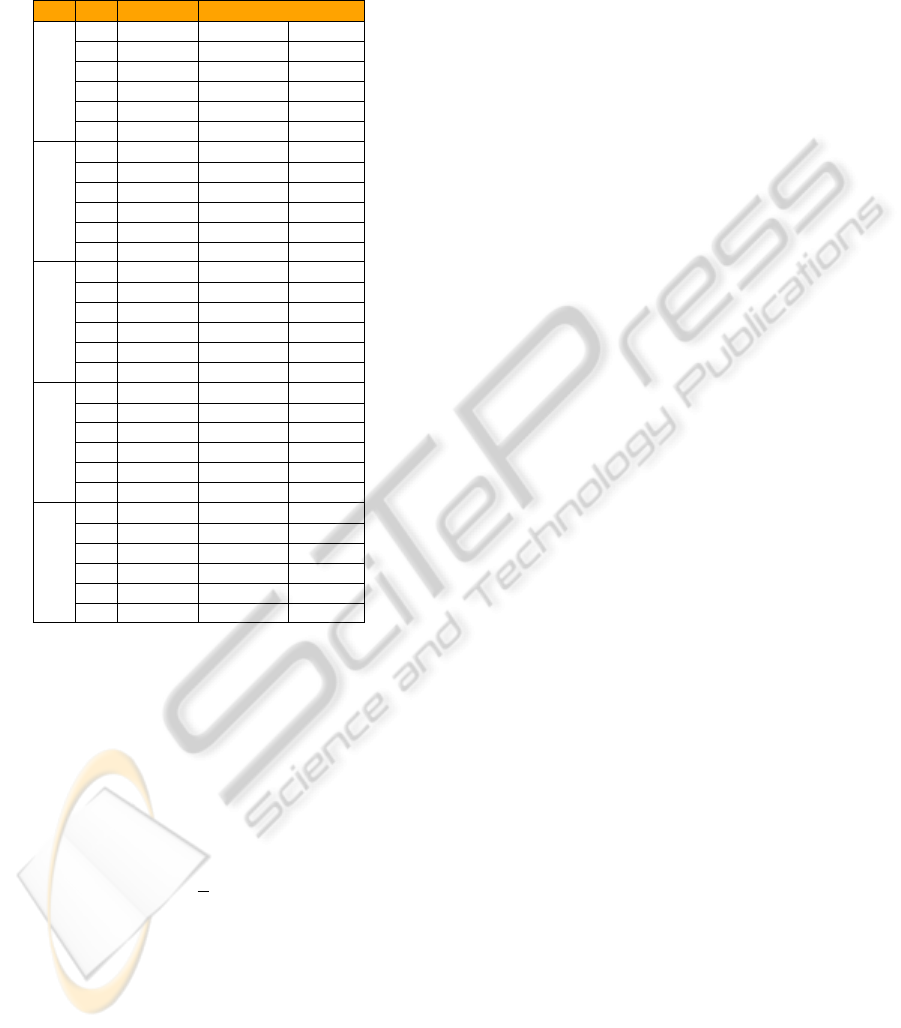
and β, as shown in Table 2, are used, generating 118
graph classification problem instances. Only the SVM
classifier is used. In Table 2 is shown a sampling of
the results, together with the total computing time for
the classification model training, with the genetic fea-
ture selection optimization, and finally the number of
selected features per single test. The average classi-
fication error is 13.75 %. The classification error in-
creases considerably, when 0 < α < 1, only for β = 1,
that is the recognition procedure exhibits a very robust
behavior. The unperformant results obtained for the
first 11 runs, that is for α = 0 and β = 0 → 1, are well
explainable. Considering Equation 2, for α = 0 we
obtain two intermediate matrices that are equal and
are again permutation matrices. For any considered
value of β in Equation 3, we obtain again the same
permutation matrices. Thus, also in this case the com-
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
190
plexity of recognition task is high, and the obtained
results confirm this fact.
Table 2: Classification Results.
α β # Feature Time (sec.) % Error
0
0.0 3850 3820 0.0
0.2 3891 6733 50.8
0.4 3951 7021 47.4
0.6 3925 7228 43.2
0.8 3877 6982 40.0
1 3964 6759 58.6
0.2
0.0 3103 2624 4.8
0.2 3145 3142 3.6
0.4 3145 3052 2.2
0.6 3231 3130 3.6
0.8 3175 3218 2.0
1 3638 2260 59.8
0.5
0.0 3774 1908 2.2
0.2 3748 1863 2.2
0.4 3789 1919 0.8
0.6 3699 1910 2.2
0.8 3716 1913 1.0
1 3891 1218 40.4
0.7
0.0 3774 2497 2.4
0.2 3697 2462 2.4
0.4 3692 2346 1.4
0.6 3754 2381 1.2
0.8 3817 2496 0.8
1 3811 1606 40.4
1
0.0 3854 1632 40.0
0.2 3848 1520 40.0
0.4 3823 1546 39.8
0.6 3801 1473 39.8
0.8 3792 1613 39.2
1 3756 1468 40.0
5 CONCLUSIONS
The obtained results, for both tests, show that this
methodology is valid, robust and accurate, showing a
controllable and predictable behavior. The two trans-
formations, that is the seriation of a graph G
i
into a
sequence of its vertices identifiers, say s
i
, and the final
mapping into the dissimilarity space E aimed at ob-
taining a histogram vector h
i
, seems to be able to cap-
ture and use the key information of the input dataset
G, generating a representation model that can be used
for different analysis. It is important to underline that
the true engine of this representation technique, that is
the GRADIS procedure, can be employed as the core
of a wider inductive modeling system, as well on its
own to solve data mining and knowledge discovery
problems. Moreover, in this paper we have described
GRADIS as a procedure able to deal with sequences
of characters. The same scheme can be adopted on
a set of more complex patterns, such as fully labeled
graphs or any other complex discrete object, once a
definition of substructure, a dissimilarity measure be-
tween two substructures and a way to represent a clus-
ter of substructures are provided. Future directions
will deal also with such a generalization and a sub-
stantial amount of effort will be devoted to the devel-
opment of a faster algorithm for the alphabet identifi-
cation step.
REFERENCES
Bargiela, A. and Pedrycz, W. (2003). Granular computing:
an introduction. Number v. 2002 in Kluwer inter-
national series in engineering and computer science.
Kluwer Academic Publishers.
Borgwardt, K. M., Ong, C. S., Sch
¨
onauer, S., Vish-
wanathan, S. V. N., Smola, A. J., and Kriegel, H.-P.
(2005). Protein function prediction via graph kernels.
Bioinformatics, 21:47–56.
Del Vescovo, G., Livi, L., Rizzi, A., and Frattale Masci-
oli, F. M. (2011). Clustering structured data with the
SPARE library. In Proceeding of 2011 4th IEEE Int.
Conf. on Computer Science and Information Technol-
ogy, volume 9, pages 413–417.
Del Vescovo, G. and Rizzi, A. (2007). Automatic classi-
fication of graphs by symbolic histograms. In Pro-
ceedings of the 2007 IEEE International Conference
on Granular Computing, GRC ’07, pages 410–416,
San Jose, CA, USA. IEEE Computer Society.
Kuramochi, M. and Karypis, G. (2002). An efficient al-
gorithm for discovering frequent subgraphs. Techni-
cal report, IEEE Transactions on Knowledge and Data
Engineering.
Neuhaus, M., Riesen, K., and Bunke, H. (2006). Fast sub-
optimal algorithms for the computation of graph edit
distance. In Structural, Syntactic, and Statistical Pat-
tern Recognition. LNCS, pages 163–172. Springer.
Pe¸kalska, E. and Duin, R. (2005). The dissimilarity rep-
resentation for pattern recognition: foundations and
applications. Series in machine perception and artifi-
cial intelligence. World Scientific.
Riesen, K. and Bunke, H. (2009). Approximate graph
edit distance computation by means of bipartite graph
matching. Image Vision Comput., 27:950–959.
Riesen, K. and Bunke, H. (2010). Graph Classification and
Clustering Based on Vector Space Embedding. Se-
ries in Machine Perception and Artificial Intelligence.
World Scientific Pub Co Inc.
Rizzi, A., Panella, M., and Frattale Mascioli, F. M. (2002).
Adaptive resolution min-max classifiers. IEEE Trans-
actions on Neural Networks, 13:402–414.
Robles-Kelly, A. and Hancock, E. R. (2005). Graph edit
distance from spectral seriation. IEEE Trans. Pattern
Anal. Mach. Intell., 27:365–378.
Vishwanathan, S. V. N., Borgwardt, K. M., Kondor, R. I.,
and Schraudolph, N. N. (2008). Graph kernels. CoRR,
abs/0807.0093.
GRAPH RECOGNITION BY SERIATION AND FREQUENT SUBSTRUCTURES MINING
191
