LEARNING TO PLAY K-ARMED BANDIT PROBLEMS
Francis Maes, Louis Wehenkel and Damien Ernst
University of Li
`
ege, Dept. of Electrical Engineering and Computer Science
Institut Montefiore, B28, B-4000, Li
`
ege, Belgium
Keywords:
Multi-armed bandit problems, Reinforcement learning, Exploration-exploitation dilemma.
Abstract:
We propose a learning approach to pre-compute K-armed bandit playing policies by exploiting prior infor-
mation describing the class of problems targeted by the player. Our algorithm first samples a set of K-armed
bandit problems from the given prior, and then chooses in a space of candidate policies one that gives the
best average performances over these problems. The candidate policies use an index for ranking the arms and
pick at each play the arm with the highest index; the index for each arm is computed in the form of a linear
combination of features describing the history of plays (e.g., number of draws, average reward, variance of
rewards and higher order moments), and an estimation of distribution algorithm is used to determine its opti-
mal parameters in the form of feature weights. We carry out simulations in the case where the prior assumes a
fixed number of Bernoulli arms, a fixed horizon, and uniformly distributed parameters of the Bernoulli arms.
These simulations show that learned strategies perform very well with respect to several other strategies pre-
viously proposed in the literature (UCB1, UCB2, UCB-V, KL-UCB and ε
n
-GREEDY); they also highlight
the robustness of these strategies with respect to wrong prior information.
1 INTRODUCTION
The exploration versus exploitation dilemma arises in
many fields such as finance, medicine, engineering as
well as artificial intelligence. The finite horizon K-
armed bandit problem formalizes this dilemma in the
most simple form (Robbins, 1952): a gambler has T
coins, and at each step he may choose among one of K
slots (or arms) to allocate one of these coins, and then
earns some money (his reward) depending on the re-
sponse of the machine he selected. Rewards are sam-
pled from an unknown probability distribution depen-
dent on the selected arm but otherwise independent of
previous plays. The goal of the gambler is simply to
collect the largest cumulated reward once he has ex-
hausted his coins (i.e. after T plays). A rational player
knowing the reward distributions of the K arms would
play at every stage an arm with maximal expected re-
ward, so as to maximize his expected cumulative re-
ward (irrespectively of the number K of arms and the
number of T coins). When the reward distributions
are unknown, it is however much less trivial to decide
how to play optimally.
Most theoretical works that have studied the K-
armed bandit problem have focused on the design
of generic policies which are provably optimal in
asymptotic conditions (large T ), independently of the
number of arms K, and assuming only some very un-
restrictive regularity conditions on the reward distri-
butions (e.g., bounded support). Among these, some
work by computing at every play a quantity called
“upper confidence index” for each arm that depends
on the rewards collected so far by this arm, and by se-
lecting for the next play (or round of plays) the arm
with the highest index. Such index-based policies
have been initially introduced by (Lai and Robbins,
1985) where the indexes were difficult to compute.
More easy to compute indexes where proposed later
on (Agrawal, 1995; Auer et al., 2002; Audibert et al.,
2007).
These “index based” policies typically involve
meta-parameters whose values impact their relative
performances. Usually, when reporting simulation re-
sults, authors manually tuned these values on prob-
lems that share similarities with their test problems
(e.g., the same type of distributions for generating the
rewards) by running trial-and-error simulations (Auer
et al., 2002; Audibert et al., 2008). In doing this, they
actually exploited prior information on the K-armed
bandit problems to select the meta-parameters.
Starting from this observation, we elaborated a
systematic approach for learning in an automatic way
good policies for playing K-armed bandit problems.
This approach explicitly exploits the prior informa-
74
Maes F., Wehenkel L. and Ernst D..
LEARNING TO PLAY K-ARMED BANDIT PROBLEMS.
DOI: 10.5220/0003733500740081
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 74-81
ISBN: 978-989-8425-95-9
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

tion on the target set of K-armed bandit problems; it
first generates a sample of problems compliant with
this prior information and then searches in a paramet-
ric set of candidate policies one that yields optimal av-
erage performances over this sample. This approach
allows to automatically tune meta-parameters of ex-
isting upper confidence indexes. But, more impor-
tantly, it opens the door for searching within a much
broader class of policies one that is optimal for a given
set of problems compliant with the prior information.
In particular, we show, in the case of Bernoulli arms,
that when the number K of arms and the playing hori-
zon T are fully specified a priori, this approach may
be very productive. We also evaluate the robustness
of the learned policies with respect to erroneous prior
assumptions.
After recalling in the next section elements related
to the K-armed bandit problem, we present in details
our approach and algorithms in Section 3. In Section
4, we report some convincing simulation results. Fi-
nally, we will conclude in Section 5 and present future
research directions.
2 THE K-ARMED BANDIT
PROBLEM
We denote by i ∈ {1,2,. .., K} the (K ≥ 2) arms of
the bandit problem, by ν
i
the reward distribution of
arm i, and by µ
i
its expected value; b
t
is the arm
played at round t, and r
t
∼ ν
b
t
is the obtained reward.
H
t
= [b
1
,r
1
,b
2
,r
2
,...,b
t
,r
t
] is a vector that gathers
the history over the first t plays, and we denote by
H the set of all possible histories of any length t.
A policy π : H →{1,2,...,K}is an algorithm that
processes at play t the vector H
t−1
to select the arm
b
t
∈ {1,2,...,K}:
b
t
= π(H
t−1
). (1)
The regret of the policy π after T plays is defined by:
R
π
T
= T µ
∗
−
T
∑
t=1
r
t
, (2)
where µ
∗
= max
k
µ
k
refers to the expected reward of
the optimal arm. The expected value of the regret rep-
resents the expected loss due to the fact that the policy
does not always play the best machine. It can be writ-
ten as:
E[R
π
T
] =
K
∑
k=1
E[T
k
(T )](µ
∗
−µ
k
), (3)
where T
k
(T ) denotes the number of times the policy
has drawn arm k on the first T rounds.
The K-armed bandit problem aims at finding a
policy π
∗
that for a given K minimizes the expected
regret (or, in other words, maximizes the expected re-
ward), ideally for any T and any {ν
i
}
K
i=1
.
3 DESCRIPTION OF OUR
APPROACH
We now introduce our approach for learning K-armed
bandit policies given a priori information on the set
of target problems. We also describe the fully spec-
ified instance of this approach that is tested in Sec-
tion 4 and compared against several other policies in-
troduced previously in the literature, namely UCB1,
UCB2 (Auer et al., 2002), UCB-V (Audibert et al.,
2007), ε
n
-GREEDY (Sutton and Barto, 1998) and vari-
ants of these policies.
3.1 Generic Description
In order to identify good bandit policies, we exploit
prior knowledge on the problem to be solved rep-
resented as a distribution D
P
over bandit problems
P = (ν
1
,...,ν
K
). From this distribution, we can sam-
ple as many bandit problems as desired. In order
to learn a policy exploiting this knowledge, we pro-
pose to proceed as follows. First, we sample a set
of training bandit problems P
(1)
,...,P
(N)
from D
P
.
This set should be large enough to be representative
of the target space of bandit problems. We then se-
lect a parametric family of candidate policies Π
Θ
⊂
{1,2,...,K}
H
whose members are policies π
θ
that
are fully defined given parameters θ ∈ Θ. We finally
solve the following optimization problem:
θ
∗
= argmin
θ∈Θ
∆(π
θ
) (4)
where ∆(π) ∈ is a loss function that computes the
empirical mean of expected regret of π on the training
set:
∆(π) =
1
N
N
∑
i=1
R
π
T
(P
(i)
) (5)
where T is the (a-priori given) time playing horizon.
Note that since R
π
T
relies on the expected values
of T
k
(t), computing ∆(π) exactly is impossible in the
general case. We therefore estimate the E[T
k
(t)] quan-
tities by averaging their observed values over a large
number of simulations, as described in Section 4.
LEARNING TO PLAY K-ARMED BANDIT PROBLEMS
75

Algorithm 1: Generic index-based discrete bandit policy.
1: Given function index : H ×{1,2,... ,K} → ,
2: for t = 1 to K do
3: Play bandit b
t
= t
4: Observe reward r
t
5: end for
6: for t = K to T do
7: b
t
= argmax
k∈{1,2,...,K}
index(H
t−1
,k)
8: Play bandit b
t
and observe reward r
t
9: end for
3.2 Family of Candidate Policies
Considered
As candidate policies we will consider policies which
are fully defined by a scoring function index : H ×
{1,2,...,K}→ . These policies are sketched in Al-
gorithm 1 and work as follows. During the first K
plays, they play sequentially the machines 1,2,...,K.
In all subsequent plays, these policies compute for ev-
ery machine k the score index(H
t−1
,k) ∈ that de-
pends on the arm k and on the previous history H
t−1
.
At each step, the arm (or one of the arms) with the
largest score is then selected.
Note that most well-known previously proposed
bandit policies are particular cases of Algorithm 1. As
an example, the policy UCB1 (Auer et al., 2002) is an
index-based bandit policy with:
index
ucb1
(H
t
,k) = ¯r
k
+
s
2lnt
T
k
, (6)
where ¯r
k
is the average reward obtained from machine
k and T
k
is the number of times machine k has been
played so far.
To define the parametric family of candidate poli-
cies Π
Θ
, we use index functions expressed as lin-
ear combinations of history features. These index
functions rely on an history feature function φ : H ×
{1,2,...,K} →
d
, that describes the history w.r.t.
a given arm as a vector of scalar features. Each
such scalar feature may describe any aspect of the
history, including empirical reward moments, current
time step, arm play counts or combinations of these
variables.
Given the function φ(·,·), index functions are de-
fined by
index
θ
(H
t
,k) =
h
θ,φ(H
t
,k)
i
, (7)
where θ ∈
d
are parameters and
h
·,·
i
is the classical
dot product operator.
The features computed by φ(·, ·) should be rele-
vant to the problem of assigning good indices to ban-
dits. The set of features should not be too large to
avoid optimization and learning difficulties related to
the large number of parameters, but it should be large
enough to provide the basis for a rich class of ban-
dit policies. We propose one particular history feature
function in Section 4 that can be used for any discrete
bandit problem and that leads to successful policies.
The set of candidate policies Π
Θ
is composed of
all index-based policies obtained with index functions
defined by Equation 7 given parameters θ ∈
d
.
3.3 Optimisation Algorithm
The optimization problem defined by Equation 4 is
a hard optimization problem, with an objective func-
tion that has a complex relation with the parameters
θ. A slight change in the parameter vector θ may
lead to significantly different bandit episodes and ex-
pected regret values. Local optimization approaches
may thus not be appropriate here. Instead, we sug-
gest the use of derivative-free global optimization al-
gorithms.
In this work, we use a powerful, yet simple,
class of global optimization algorithms known as Es-
timation of Distribution Algorithms (EDA) (Gonzalez
et al., 2002). EDAs rely on a probabilistic model to
describe promising regions of the search space and to
sample good candidate solutions. This is performed
by repeating iterations that first sample a population
of n
p
candidates using the current probabilistic model
and then fit a new probabilistic model given the b < n
p
best candidates.
Any kind of probabilistic model may be used in-
side an EDA. The simplest form of EDAs uses one
marginal distribution per variable to optimize and is
known as the univariate marginal distribution algo-
rithm (Pelikan and M
¨
uhlenbein, 1998). We have
adopted this approach by using one Gaussian distribu-
tion N (µ
p
,σ
2
p
) for each parameter θ
p
. Although this
approach is simple, it proved to be quite effective ex-
perimentally to solve Equation 4. The full details of
our EDA-based policy learning procedure are given
by Algorithm 2. The initial distributions are standard
Gaussian distributions N (0,1). The policy that is re-
turned corresponds to the θ parameters that led to the
lowest observed value of ∆(π
θ
).
4 NUMERICAL EXPERIMENTS
The aim of this Section is to show that the expected re-
gret can significantly be improved by exploiting prior
knowledge on bandit problems, and that learning gen-
eral index-based policies with a large number of pa-
rameters outperforms careful tuning of all previously
ICAART 2012 - International Conference on Agents and Artificial Intelligence
76

Algorithm 2: EDA-based learning of a discrete bandit pol-
icy.
Given the number of iterations i
max
,
Given the population size n
p
,
Given the number of best elements b,
Given a sample of training bandit problems
P
(1)
,...,P
(N)
,
Given an history-features function φ(·,·) ∈
d
,
// Initialize with normal Gaussians
1: for each parameter p ∈[1, d] do
2: µ
p
= 0
3: σ
2
p
= 1
4: end for
5: for i ∈ [1,i
max
] do
// Sample and evaluate new population
6: for j ∈ [1, n
p
] do
7: for p ∈[1,d] do
8: θ
p
= sample from N (µ
p
,σ
2
p
)
9: end for
10: Estimate ∆(π
θ
)
11: Store θ along with ∆(π
θ
)
12: end for
// Select best candidates
13: Select {θ
(1)
,...,θ
(b)
} the b best candidate θ
vectors w.r.t. their ∆(·) score
// Learn new Gaussians
14: for each parameter p ∈[1,d] do
15: µ
p
=
1
b
∑
b
j=1
θ
( j)
p
16: σ
2
p
=
1
b
∑
b
j=1
(θ
( j)
p
−µ
p
)
2
17: end for
18: end for
19: return The policy π
θ
with θ the parameters that
led to the lowest observed value of ∆(θ)
proposed simple bandit policies.
To illustrate our approach, we consider the sce-
nario where the number of arms, the playing horizon
and the kind of distributions ν
i
are known a priori and
where the parameters of these distributions is missing
information. In particular, we focus on two-arms ban-
dit problems with Bernoulli distributions whose ex-
pectations are uniformly drawn from [0,1]. Hence, in
order to sample a bandit problem from D
P
, we draw
the expectations p
1
and p
2
uniformly from [0, 1] and
return the bandit problem defined by two-Bernoulli
arms with p
1
and p
2
.
Baselines. We consider the following baseline poli-
cies: the ε
n
-GREEDY policy Sutton and Barto, 1998
as described in (Auer et al., 2002), the policies in-
troduced by (Auer et al., 2002): UCB1, UCB1-
BERNOULLI
1
, UCB1-NORMAL and UCB2, the
policy KL-UCB introduced in (Garivier and Capp
´
e,
2011) and the policy UCB-V proposed by (Audib-
ert et al., 2007). Except ε
n
-GREEDY, all these poli-
cies belong to the family of index-based policies dis-
cussed in the previous Section. UCB1-BERNOULLI
and UCB1-NORMAL are parameter-free policies de-
signed for bandit problems with Bernoulli distribu-
tions and for problems with Normal distributions
respectively. All the other policies have meta-
parameters that can be tuned to improve the quality
of the policy. ε
n
-GREEDY has two parameters c > 0
and 0 < d < 1, UCB2 has one parameter 0 < α < 1,
KL-UCB has one parameter c ≥ 0 and UCB-V has
two parameters ζ > 0 and c > 0. We refer the reader
to (Auer et al., 2002; Audibert et al., 2007; Garivier
and Capp
´
e, 2011) for detailed explanations of these
parameters. For the tunable version of UCB1, we use
the following formula:
index
ucb1(C)
(H
t
,k) = ¯r
k
+
s
C lnt
T
k
(8)
where C > 0 is the meta-parameter to tradeoff be-
tween exploration and exploitation.
Tuning / Training Procedure. To make our com-
parison fair, we use the same tuning / training pro-
cedure for all the policies, which is Algorithm 2
with i
max
= 100 iterations, n
p
= max(8d,40) candi-
date policies per iteration and b = n
p
/4 best elements,
where d is the number of parameters to optimize.
Having a linear dependency between n
p
and d is a
classical choice when using EDAs (Rubenstein and
Kroese, 2004). Note that, in most cases the optimiza-
tion is solved in a few or a few tens iterations. Our
simulations have shown that i
max
= 100 is a careful
choice for ensuring that the optimization has enough
time to properly converge. For the baseline poli-
cies where some default values are advocated, we use
these values as initial expectation of the EDA Gaus-
sians. Otherwise, the initial Gaussians are centered
on zero. Nothing is done to enforce the EDA to re-
spect the constraints on the parameters (e.g., c > 0 and
0 < d < 1 for ε
n
-GREEDY). In practice, the EDA au-
tomatically identifies interesting regions of the search
space that respect these constraints.
History Features Function. We now detail the par-
ticular φ(·, ·) function that we used in our experiments
1
The original name of this policy is UCB-TUNED.
Since this paper mostly deals with policies having parame-
ters, we changed the name to UCB1-BERNOULLI to make
clear that no parameter tuning has to be done with this pol-
icy.
LEARNING TO PLAY K-ARMED BANDIT PROBLEMS
77

and that can be applied to any discrete bandit problem.
To compute φ(H
t
,k), we first compute the following
four variables:
v
1
=
√
lnt v
2
=
r
1
T
k
v
3
= ¯r
k
v
4
=
¯
ρ
k
i.e. the square root of the logarithm of the current
time step, the inverse square root of the number of
times arm k has been played, the empirical mean and
standard deviation of the rewards obtained so far by
arm k.
Then, these variables are multiplied in different
ways to produce features. The number of these com-
binations is controlled by a parameter P whose default
value is 1. Given P, there is one feature f
i, j,k,l
per pos-
sible combinations of values of i, j,k,l ∈ {0, ... ,P},
which is defined as follows:
f
i, j,k,l
= v
i
1
v
j
2
v
k
3
v
l
4
(9)
In the following, we denote POWER-1 (resp.,
POWER-2) the policy learned using function φ(H
t
,k)
with parameter P = 1 (resp., P = 2). The index func-
tion that underlies these policies can be written as fol-
lowing:
index
power
(H
t
,k) =
P
∑
i=0
P
∑
j=0
P
∑
k=0
P
∑
l=0
θ
i, j,k,l
v
i
1
v
j
2
v
k
3
v
l
4
(10)
where θ
i, j,k,l
are the learned parameters. The
POWER-1 policy has 16 such parameters and the
POWER-2 has 81 parameters.
Training and Testing Sets. Since we are learning
policies, care should be taken with generalization is-
sues. As usual in supervised machine learning, we
use a training set which is distinct from the testing
set. The training set is composed of N = 100 bandit
problems sampled from D
P
whereas the testing set
contains another 10000 problems. When computing
∆(π
θ
), we estimate the regret for each of these prob-
lems by averaging results overs 100 runs. One cal-
culation of ∆(π
θ
) thus involves simulating 10
4
(resp.
10
6
) bandit episodes during training (resp. testing).
4.1 Results
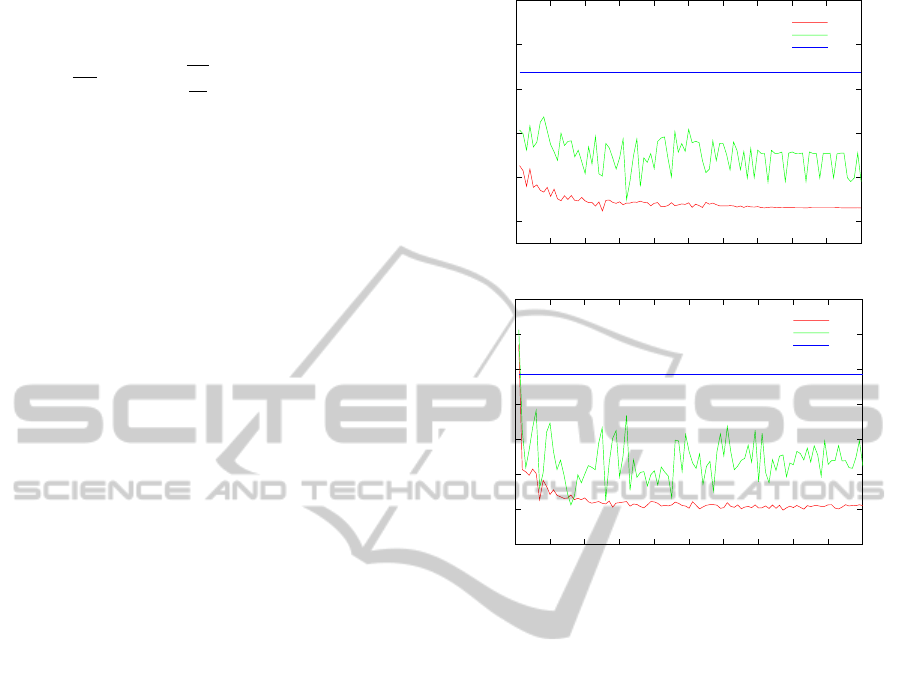
Typical Run of the Learning Algorithm. Figure 1
illustrates typical runs of Algorithm 2 when learn-
ing POWER-1. The curves represent the best regret
achieved at each iteration of the EDA. The EDA op-
timizes the train regret and is not aware of the test
regret score, which thus truly evaluates how well the
learned policy generalizes to new bandit problems.
1.6
1.8
2
2.2
2.4
2.6
0 10 20 30 40 50 60 70 80 90 100
Mean regret
EDA Iterations
Train regret
Test regret
Test regret with UCB1-Bernoulli
3
3.5
4
4.5
5
5.5
6
6.5
0 10 20 30 40 50 60 70 80 90 100
Mean regret
EDA Iterations
Train regret
Test regret
Test regret with UCB1-Bernoulli
Figure 1: Training and testing regret of POWER-1 as a func-
tion of the number of EDA iterations. Left: training horizon
100. Right: training horizon 1000.
Note that to make things slightly faster, we only eval-
uated the test regrets roughly in this experiment, by
doing a single run (instead of 100) per testing prob-
lem. See below for precise test regret values. As a
matter of comparison, we also display the test regret
achieved by the policy UCB1-BERNOULLI, which
was especially designed for Bernoulli bandit prob-
lems.
We observe a common phenomenon of machine
learning: the learned policy behaves slightly better on
training problems than on testing problems. This ef-
fect could be reduced by using a larger set of training
problems. However, it can be seen that the test regrets
are already significantly better than those achieved by
UCB1-BERNOULLI. Furthermore, it can be seen that
a few iterations are sufficient to find POWER-1 poli-
cies that outperform this baseline. For example, on
the left curve, at iteration 1 the EDA test regret is
already better then the baseline regret. This means
that, in this experiment, sampling 8d = 128 random
POWER-1 policies was enough to find at least one pol-
icy outperforming UCB1-BERNOULLI.
We used a C++ based implementation to perform
our experiments. With 10 cores at 1.9Ghz, perform-
ICAART 2012 - International Conference on Agents and Artificial Intelligence
78

Table 1: Mean expected regret of untuned, tuned and learned policies on Bernoulli and Gaussian bandit problems. Best scores
in each of these categories are shown in bold. Scores corresponding to policies that are tested on the same horizon T than the
horizon used for training/tuning are shown in italics.
Policy Training Parameters Bernoulli Gaussian
Horizon T=10 T=100 T=1000 T=10 T=100 T=1000
Untuned policies
UCB1 - C = 2 1.07 5.57 20.1 1.37 10.6 66.7
UCB1-BERNOULLI - 0.75 2.28 5.43 1.09 6.62 37.0
UCB1-NORMAL - 1.71 13.1 31.7 1.65 13.4 58.8
UCB2 - α = 10
−3
0.97 3.13 7.26 1.28 7.90 40.1
UCB-V - c = 1,ζ = 1 1.45 8.59 25.5 1.55 12.3 63.4
KL-UCB - c = 0 0.76 2.47 6.61 1.14 7.66 43.8
KL-UCB - c = 3 0.82 3.29 9.81 1.21 8.90 53.0
ε
n
-GREEDY - c = 1, d = 1 1.07 3.21 11.5 1.20 6.24 41.4
Tuned policies
T=10 C = 0.170 0.74 2.05 4.85 1.05 6.05 32.1
UCB1 T=100 C = 0.173 0.74 2.05 4.84 1.05 6.06 32.3
T=1000 C = 0.187 0.74 2.08 4.91 1.05 6.17 33.0
T=10 α = 0.0316 0.97 3.15 7.39 1.28 7.91 40.5
UCB2 T=100 α = 0.000749 0.97 3.12 7.26 1.33 8.14 40.4
T=1000 α = 0.00398 0.97 3.13 7.25 1.28 7.89 40.0
T=10 c = 1.542,ζ = 0.0631 0.75 2.36 5.15 1.01 5.75 26.8
UCB-V T=100 c = 1.681,ζ = 0.0347 0.75 2.28 7.07 1.01 5.30 27.4
T=1000 c = 1.304, ζ = 0.0852 0.77 2.43 5.14 1.13 5.99 27.5
T=10 c = −1.21 0.73 2.14 5.28 1.12 7.00 38.9
KL-UCB T=100 c = −1.82 0.73 2.10 5.12 1.09 6.48 36.1
T=1000 c = −1.84 0.73 2.10 5.12 1.08 6.34 35.4
T=10 c = 0.0499,d = 1.505 0.79 3.86 32.5 1.01 7.31 67.57
ε
n
-GREEDY T=100 c = 1.096,d = 1.349 0.95 3.19 14.8 1.12 6.38 46.6
T=1000 c = 0.845,d = 0.738 1.23 3.48 9.93 1.32 6.28 37.7
Learned policies
T=10 .. . 0.72 2.29 14.0 0.97 5.94 49.7
POWER-1 T=100 (16 parameters) 0.77 1.84 5.64 1.04 5.13 27.7
T=1000 .. . 0.88 2.09 4.04 1.17 5.95 28.2
T=10 .. . 0.72 2.37 15.7 0.97 6.16 55.5
POWER-2 T=100 (81 parameters) 0.76 1.82 5.81 1.05 5.03 29.6
T=1000 .. . 0.83 2.07 3.95 1.12 5.61 27.3
Table 2: Regret and percentage of wins against UCB1-BERNOULLI of tuned and learned policies.
Policy T = 10 T = 100 T = 1000
Regret Win % Regret Win % Regret Win %
UCB1-BERNOULLI 0.75 - 2.28 - 5.43 -
Tuned policies
UCB1 0.75 48.1 % 2.06 78.1 % 4.91 83.1 %
UCB2 0.97 12.7 % 3.12 6.8 % 7.25 6.8 %
UCB-V 0.75 38.3 % 2.28 57.2 % 5.14 49.6 %
KL-UCB 0.73 50.5 % 2.10 65.0 % 5.12 67.0 %
ε
n
-GREEDY 0.79 37.5 % 3.19 14.1 % 9.93 10.7 %
Learned policies
POWER-1 0.72 54.6 % 1.84 82.3 % 4.04 91.3 %
POWER-2 0.72 54.2 % 1.82 84.6 % 3.95 90.3 %
ing the whole learning (and testing) of POWER-1 took
one hour for T = 100 and ten hours for T = 1000.
Untuned, Tuned and Learned Policies. Table 1
compares three classes of discrete bandit policies:
untuned policies, tuned policies and learned poli-
LEARNING TO PLAY K-ARMED BANDIT PROBLEMS
79

cies. Untuned policies are either policies that are
parameter-free or policies used with default param-
eters suggested in the literature. Tuned policies are
the baselines that were tuned using Algorithm 2 and
learned policies comprise POWER-1 and POWER-2.
For each policy, we compute the mean expected re-
gret on two kind of bandit problems: the 10000 test-
ing problems drawn from D
P
and another set of 10000
problems with a different kind of underlying reward
distribution: truncated Gaussians to the interval [0, 1]
(that means that if you draw a reward which is outside
of this interval, you throw it away and draw a new
one). In order to sample one such problem, we select
the mean and the standard deviation of the Gaussian
distributions uniformly in range [0, 1]. For all poli-
cies except the untuned ones, we have used three dif-
ferent training horizons values T = 10, T = 100 and
T = 1000.
As already pointed out in (Auer et al., 2002), it
can be seen that UCB1-BERNOULLI is particularly
well fitted to bandit problems with Bernoulli distri-
butions. It also proves effective on bandit problems
with Gaussian distributions, making it nearly always
outperform the other untuned policies. By tuning
UCB1, we outperform the UCB1-BERNOULLI pol-
icy (e.g. 4.91 instead of 5.43 on Bernoulli problems
with T = 1000). This also sometimes happens with
UCB-V. However, though we used a careful tuning
procedure, UCB2 and ε
n
-GREEDY do never outper-
form UCB1-BERNOULLI.
When using the same training and testing hori-
zon T , POWER-1 and POWER-2 systematically out-
perform all the other policies (e.g. 1.82 against 2.05
when T=100 and 3.95 against 4.91 when T = 1000).
Robustness w.r.t. the Horizon T . As expected, the
learned policies give their best performance when the
training and the testing horizons are equal. When the
testing horizon is larger than the training horizon, the
quality of the policy may quickly degrade (e.g. when
evaluating POWER-1 trained with T = 10 on an hori-
zon T = 1000), the inverse being less maked.
Robustness w.r.t. the Kind of Distribution. Al-
though truncated Gaussian distributions are signif-
icantly different from Bernoulli distributions, the
learned policies most of the time generalize well to
this new setting and still outperform all the other poli-
cies.
Robustness w.r.t. to the Metric. Table 2 gives
for each policy, its regret and its percentage of wins
against UCB1-BERNOULLI, when trained with the
same horizon as the test horizon. To compute the
percentage of wins against UCB1-BERNOULLI, we
evaluate the expected regret on each of the 10000
testing problems and count the number of prob-
lems for which the tested policy outperforms UCB1-
BERNOULLI. We observe that by minimizing the ex-
pected regret, we have also reached large values of
percentage of wins: 84.6 % for T = 100 and 91.3 %
for T = 1000. Note that, in our approach, it is easy
to change the objective function. So if the real ap-
plicative aim was to maximize the percentage of wins
against UCB1-BERNOULLI, this criterion could have
been used directly in the policy optimization stage to
reach even better scores.
5 CONCLUSIONS
The approach proposed in this paper for exploiting a
priori information for learning policies for K-armed
bandit problems has been tested when knowing the
time horizon and that arms rewards were generated
by Bernoulli distributions. The learned policies were
found to significantly outperform other policies pre-
viously published in the literature such as UCB1,
UCB2, UCB-V, KL-UCB and ε
n
-GREEDY. The ro-
bustness of the learned policy with respect to wrong
information was also highlighted.
There are in our opinion several research direc-
tions that could be investigated for still improving the
algorithm for learning policies proposed in this paper.
For example, we found out that problems similar to
the problem of overfitting met in supervised learning
could occur when considering a too large set of candi-
date polices. This naturally calls for studying whether
our learning approach could be combined with regu-
larization techniques. More sophisticated optimizers
could also be thought of for identifying in the set of
candidate policies, the one which is predicted to be-
have at best.
The UCB1, UCB2, UCB-V, KL-UCB and ε
n
-
GREEDY policies used for comparison can be shown
(under certain conditions) to have interesting bounds
on their expected regret under asymptotic conditions
(very large T ) while we did not provide such bounds
for our learned policy. It would certainly be rele-
vant to investigate whether similar bounds could be
derived for our learned policies or, alternatively, to
see how the approach could be adapted so as to have
learned policies that have strong theoretical perfor-
mance guarantees. For example, better bounds on the
expected regret could perhaps be obtained by identi-
fying in a set of candidate policies the one that gives
the smallest maximal value of the expected regret over
this set rather than the one that gives the best average
performances.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
80

Finally, we suggest also to extend our policy
learning scheme to other – and more complex –
exploration-exploitation problems than the one tack-
led in this paper, such as for example bandit prob-
lems where the arms are not statistically independent
(Mersereau et al., 2009) or general Markov Decision
processes (Ishii et al., 2002).
REFERENCES
Agrawal, R. (1995). Sample mean based index policies with
o(log n) regret for the multi-armed bandit problem.
Advances in Applied Mathematics, 27:1054–1078.
Audibert, J., Munos, R., and Szepesvari, C. (2007). Tuning
bandit algorithms in stochastic environments. Algo-
rithmic Learning Theory (ALT), pages 150–165.
Audibert, J., Munos, R., and Szepesvari, C. (2008).
Exploration-exploitation trade-off using variance esti-
mates in multi-armed bandits. Theoretical Computer
Science.
Auer, P., Fischer, P., and Cesa-Bianchi, N. (2002). Finite-
time analysis of the multi-armed bandit problem. Ma-
chine Learning, 47:235–256.
Garivier, A. and Capp
´
e, O. (2011). The KL-UCB algorithm
for bounded stochastic bandits and beyond. CoRR,
abs/1102.2490.
Gonzalez, C., Lozano, J., and Larra
˜
naga, P. (2002). Estima-
tion of Distribution Algorithms. A New Tool for Evo-
lutionary Computation, pages 99–124. Kluwer Aca-
demic Publishers.
Ishii, S., Yoshida, W., and Yoshimoto, J. (2002). Control of
exploitation-exploration meta-parameter in reinforce-
ment learning. Neural Networks, 15:665–687.
Lai, T. and Robbins, H. (1985). Asymptotically efficient
adaptive allocation rules. Advances in Applied Math-
ematics, 6:4–22.
Mersereau, A., Rusmevichientong, P., and Tsitsiklis, J.
(2009). A structured multiarmed bandit problem and
the greedy policy. IEEE Trans. Automatic Control,
54:2787–2802.
Pelikan, M. and M
¨
uhlenbein, H. (1998). Marginal distri-
butions in evolutionary algorithms. In Proceedings of
the International Conference on Genetic Algorithms
Mendel ’98, pages 90–95, Brno, Czech Republic.
Robbins, H. (1952). Some aspects of the sequential design
of experiments. Bulletin of The American Mathemat-
ical Society, 58:527–536.
Rubenstein, R. and Kroese, D. (2004). The cross-entropy
method : a unified approach to combinatorial op-
timization, Monte-Carlo simluation, and machine
learning. Springer, New York.
Sutton, R. and Barto, A. (1998). Reinforcement Learning:
An Introduction. MIT Press.
LEARNING TO PLAY K-ARMED BANDIT PROBLEMS
81