IMPACT OF BLOCKING WHEN CUSTOMERS OF DIFFERENT
CLASSES ARE ACCOMMODATED IN ONE COMMON QUEUE
Herwig Bruneel, Willem M´elange, Bart Steyaert, Dieter Claeys and Joris Walraevens
Department of Telecommunications and Information Processing
Ghent University-UGent, Ghent, Belgium
Keywords:
Queueing model, Blocking, Class clustering.
Abstract:
In this paper, situations are investigated where customers requiring different types of service, each provided
by distinct servers, are accommodated in one common queue. In such scenarios, customers of one class (i.e.,
requiring a given type of service) may be hindered (“blocked”) by customers of other classes. For instance, if
a road or a highway is split in two or more subroads leading to different destinations, cars on that road heading
for destination A may be hindered or even blocked by cars heading for destination B, even when the subroad
leading to destination A is free, simply because they have to queue in first-come-first-served (FCFS) order on
the main road.
The purpose of this paper is to study the effect of blocking. We therefore develop a discrete-time queueing
model and establish performance measures related to the number of waiting customers. Based on the obtained
results, we demonstrate that clustering of arrivals according to class pronounces the negative impact of block-
ing. We believe that the impact of class clustering on blocking has been largely overlooked in the regular
operations research and queueing literature.
1 INTRODUCTION
In general, when customers require some kind of ser-
vice, they queue up and await their turn. This can
range from people waiting at a counter of a post office
to cars waiting at traffic lights. When a variety of ser-
vices is provided, usually separate queues are formed
for each service type. For instance, in a City Hall, dif-
ferent queues are created for the Register Office and
the Housing Department. In some applications how-
ever, it may not be physically feasible or desirable to
provide separate queues for each type of service that
customers may require, and it may be necessary or de-
sirable to accommodate different types of customers
(i.e., customers requiring different types of service) in
the same queue. In such cases, customers of one type
(i.e., requiring a given type of service) may also be
hindered by customers of other types. For instance,
if a road or a highway is split in two or more sub-
roads leading to different destinations, cars on that
road heading for destination A may be hindered or
even blocked by cars heading for destination B, even
when the subroad leading to destination A is free,
simply because they have to queue in first-come-first-
served (FCFS) order on the main road. This block-
ing also takes place in weaving sections on highways
(Ngoduy, 2006; Nishi et al., 2009). We refer to (Van
Woensel and Vandaele, 2006; Van Woensel and Van-
daele, 2007) for a general overview and validation of
the modelling of traffic flows with queueing models.
Similarly, in switching nodes of telecommunication
networks, information packets with a given destina-
tion A may have to wait for the transmission of pack-
ets destined to node B that arrived earlier, even when
the link to destination A is free, if the arriving pack-
ets are accommodated in so-called input queues ac-
cording to the source from which they originate (the
well-known HOL-blocking effect, see (Karol et al.,
1987; Liew, 1994; Laevens, 1999; Stolyar, 2004;
Beekhuizen and Resing, 2009)). These situations are
also related to models where queues are “pooled” (see
e.g. (Mandelbaum and Reiman, 1998; Van Dijk and
Van der Sluis, 2008)) in the sense that customers (cars
or packets) that require a different service or have
a different destination share a common queue. Al-
though the queue studied in the current paper can be
considered as pooled, the difference with the mod-
els in (Mandelbaum and Reiman, 1998; Van Dijk and
Van der Sluis, 2008) is that customers can be blocked
by customers of the other type.
In order to gain insight into the impact of this kind
of phenomenon on the performance of the involved
31
Bruneel H., Mélange W., Steyaert B., Claeys D. and Walraevens J..
IMPACT OF BLOCKING WHEN CUSTOMERS OF DIFFERENT CLASSES ARE ACCOMMODATED IN ONE COMMON QUEUE.
DOI: 10.5220/0003735500310038
In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 31-38
ISBN: 978-989-8425-97-3
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

systems, we study the number of customers in a sim-
ple conceptual discrete-time queueing model in this
paper, which is simple enough to allow explicit solu-
tion but rich enough to capture the essential aspects
of the problem at hand. We envisage to analyze more
general models in future work.
2 MATHEMATICAL MODEL
We consider a discrete-time queueing system with
infinite waiting room, two servers, named A and B,
and two types (classes) of customers, named 1 and 2.
Each of the two servers is dedicated to a given class of
customers, i.e., server A can only serve customers of
type 1 and server B can only serve customers of type
2. Service times of all customers are deterministically
equal to 1 slot each. Customers are served in their or-
der of arrival, regardless of the class they belong to.
We call this service discipline “global FCFS” in this
paper.
The arrival process of new customers in the sys-
tem is characterized in two steps.
First, we model the total (aggregated) arrival
stream of new customers by means of a sequence of
i.i.d. discrete random variables with common prob-
ability mass function (pmf) e(n) and common prob-
ability generating function (pgf) E(z) respectively.
More specifically,
e(n) , Prob[n arrivals in one slot] , n ≥ 0 ,
E(z) ,
∞
∑
n=0
e(n)z
n
.
The total mean number of arrivals per slot, in the
sequel referred to as the mean arrival rate, is given by
λ = E
′
(1) .
Next, we describe the occurrence of the two types
(1 and 2) in the sequence of the consecutive arriving
customers. In this first study, we assume that both
types of customers account for half of the total load of
the system, i.e., both customer classes are equiprob-
able, but there may be some degree of “class clus-
tering” in the arrival process, i.e., customers of any
given type may (or may not) have a tendency to “ar-
rive back-to-back”. Mathematically, this means that
the types of two consecutive customers may be non-
independent. Specifically, we assume a first-order
Markovian type of correlation between the types of
two consecutive customers, which basically means
that the probability that the next customer belongs to
a given class depends on the class of the previous cus-
tomer. In order to keep the model as simple as possi-
ble, we denote by α the probability that the next cus-
tomer has the same type as the previous one, and by
1− α the probability that the next customer belongs
to the opposite type as the previous one. The param-
eter α can then be considered as a measure of the de-
gree of class clustering in the arrival process, and will
therefore be referred to as the “cluster parameter” in
the sequel. It is easily seen that the size of a clus-
ter of customers of the same type, i.e., the number of
consecutive customers of any given type between two
customers of the opposite type, is geometrically dis-
tributed with parameter α and mean value 1/(1− α).
We note at this point that more general models
could be envisaged to describe the presence of class
clustering in the arrival process of the system. For in-
stance, the transition probability to go from class 1 to
1 (e.g. α) could be chosen different from the transi-
tion probability to go from class 2 to 2 (e.g. β), and
this would allowus to consider systems where the par-
tial loads of both classes of customers are not equal,
but preliminary research has revealed that this kind of
generalization would complicate the analysis of the
system considerably. More specifically, the analytical
approach to analyze the system, as presented in the
next section, would not be applicable at all. We there-
fore prefer to defer more general models to future
work. From the conceptual point of view, the only
price we pay with this choice is that we can only study
cases where both classes of customers are equiprob-
able. The effect of class clustering on the other hand
can be researched thoroughly.
It can be seen that the two-serversystem described
above is non-workconserving, for two different (or-
thogonal) reasons. First, the fact that the two servers
A and B are dedicated to only one type of customers
each, may result in situations where only one of the
servers is active even though the system contains
more than one customer (of the same type, in such
a case). This implies that we cannot expect the sys-
tem to perform as well as a regular two-server queue
with two equivalent servers, i.e., servers able to serve
all customers. In this paper, we consider this form of
inefficiency as an intrinsic feature of our system, sim-
ply caused by the fact that the customers as well as the
servers are non-identical. The second reason why the
system is non-workconserving lies in the use of the
global FCFS service discipline. This rule may result
in situations where only one server is active although
the system contains customers of both classes. Such
situations occur whenever the two “eldest” customers
in the system, i.e., the two customers at the front of
the queue, are of the same type: only one of them
can then be served (by its own dedicated server) and
the other “blocks” the access to the second server for
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
32

time
slot k
u
k
u
k+1
e
k
r
k
Figure 1: Time axis to illustrate the system equations.
customers of the opposite type further in the queue.
This second form of inefficiency is not an intrinsic
feature of two-class systems with dedicated servers,
but rather it is due to the accidental order in which
customers of both types happen to arrive (and receive
service) in the system (as described by the parameter
α in our model). It is this second mechanism that we
want to emphasize in the paper.
The structure of the rest of this paper is as fol-
lows. Section 3 first presents a general analysis of the
number of customers in the system: an expression is
derived for the pgf of this number and a method is de-
scribed to determine the two remaining unknowns in
that expression. Next, for the special case of geomet-
ric arrivals, explicit closed-form expressions are ob-
tained not only for the pgf but also for the pmf and the
mean value of the number of customers in the system.
We discuss the results both conceptually and quanti-
tatively in section 4. Some conclusions are drawn and
directions for future work are given in section 5.
3 SYSTEM ANALYSIS
3.1 System Equations
We start the analysis by defining a number of impor-
tant random variables, illustrated in Fig. 1. Specif-
ically, let u
k
denote the total system occupancy, i.e.,
the total number of customers present in the system at
the beginning of the k-th slot, and e
k
the total number
of arrivals in the system during this slot (with known
pmf e(n) and pgf E(z)). Furthermore, let r
k
(initially)
denote the number of customers served during the k-
th slot, when u
k
> 1. Then the following recursive
system equations can be established:
u
k+1
= e
k
, if u
k
≤ 1 ,
u
k+1
= u
k
+ e
k
− r
k
, if u
k
> 1 .
The two above cases can be summarized in one
single system equation
u
k+1
= e
k
+ (u
k
− r
k
)
+
, (1)
by introducing the notation (. . .)
+
to indicate the
quantity max(0,...). In equation (1), the ran-
dom variables {r
k
} can be treated as a sequence of
strictly positive i.i.d. random variables (indicating the
numbers of “available servers” during the consecutive
slots) with common pmf
r(n) , Prob[r
k
= n] , 1 ≤ n ≤ 2 ,
and common pgf
R(z) ,
2
∑
n=1
r(n) z
n
,
whereby
r(1) = α , r(2) = 1− α ,
and
R(z) = αz+ (1− α)z
2
. (2)
In fact, this observation is the key to the solution.
It actually turns out that the number of customers that
can be served in slot k (with u
k
> 1) does not depend
on the actual type of the customer in the head-of-line
position, but only on the identity or non-identity of
the classes to which the two “eldest” customers (at the
front of the queue) belong, regardless of the numbers
of customers served during previous slots. If both cus-
tomers belong to the same class, which happens with
probability α, irrespective of the type of the head-of-
line customer, then only one customer can be served.
If the two customers belong to opposite classes, then
both will be served; this case occurs with probability
1− α. This explains why r(1) = α and r(2) = 1− α.
It is clear that equation (1) is also correct if u
k
≤ 1, be-
cause, with the given definition of the r
k
’s, (u
k
− r
k
)
+
is equal to zero in such cases.
The fact that the random variables {r
k
} are inde-
pendent, in spite of the correlated nature of the types
of consecutive customers, stems from the fact that -
in this particular model - the probability that the next
customer has the same type as the previous customer
is simply given by the cluster parameter α, regardless
of the specific type of the previous customer. This
simplifying circumstance does not exist in more gen-
eral models for the “class clustering” mechanism.
3.2 Analysis of the System Occupancy
For all k, let U
k
(z) denote the pgf of u
k
. Then, from
equation (1) we can derive
U
k+1
(z) = E(z) · E
h
z
(u
k
−r
k
)
+
i
, (3)
with E[·] the expectation operator. The second factor
in the right hand side of (3) can be expanded further
IMPACT OF BLOCKING WHEN CUSTOMERS OF DIFFERENT CLASSES ARE ACCOMMODATED IN ONE
COMMON QUEUE
33

by means of the law of total probability (using also
the mutual independence of u
k
and r
k
):
E
h
z
(u
k
−r
k
)
+
i
= αE
h
z
(u
k
−1)
+
i
+ (1− α)E
h
z
(u
k
−2)
+
i
.
(4)
Here, the two remaining expectations are to be taken
with respect to one single random variable u
k
. Using
standard z-transform techniques in equation (4), and
combining the result with (3), we then obtain
U
k+1
(z) = E(z)·

R(1/z)U
k
(z) +
z− 1
z
2

(z+ 1− α)u
k
(0)
+(1− α)zu
k
(1)


, (5)
where, for all i ≥ 0,
u
k
(i) , Prob[u
k
= i] .
Now, let us assume that the queueing system at
hand is stable, i.e., that the stability condition is ful-
filled. It is not difficult to see that, with the system
equations established above, the system is stable if
and only if the mean number of arrivals per slot, given
by E
′
(1), is strictly less than the mean number of
available servers per slot, given by R
′
(1), i.e., if and
only if
E
′
(1) < R
′
(1) ,
or, expressed in the basic parameters of our system,
λ < 2− α . (6)
We now let the time parameter k go to infinity. As-
suming the system reaches a steady state, then both
functions U
k
(z) and U
k+1
(z) converge to a common
limit function U(z), which denotes the pgf of the sys-
tem occupancy at the beginning of an arbitrary slot in
steady state. As a result, equation (5) translates into a
linear equation for U(z), with solution
U(z) =
(z− 1)E(z) [u(0)(z+ 1− α) + u(1)(1− α)z]
z
2
− (1− α+ αz)E(z)
,
(7)
where
u(i) , lim
k→∞
u
k
(i) .
This expression contains only known quantities,
except for the two unknown probabilities u(0) and
u(1). These can be determined, in general, by invok-
ing the well-known property that pgf’s such as U(z)
are bounded inside the closed unit disk {z : |z| ≤ 1}
of the complex z-plane, at least when the stability
condition (6) of the queueing system is met (only in
such a case our analysis was justified and U(z) can
be viewed as a legitimate pgf). Now, it can be shown
by means of Rouch´e’s theorem from complex analy-
sis (Gonz´ales, 1992; Bruneel and Kim, 1993) that the
denominator of equation (7) has exactly two zeroes
inside the closed unit disk of the complex z-plane, one
of which is equal to 1, as soon as the stability condi-
tion (6) is fulfilled. It is clear that these two zeroes
should also be zeroes of the numerator of equation
(7), asU(z) must remain bounded in those points. For
the zero z = 1, this condition is fulfilled regardless of
the values of the unknowns u(0) and u(1), since the
numerator of (7) contains a factor z− 1. However, for
the second zero, the requirement that the numerator
should vanish yields a linear equation for the two un-
knowns. A second linear equation can be obtained by
invoking the normalizing condition of the pgf U(z),
i.e., the condition U(1) = 1. In general, the two un-
known probabilities u(0) and u(1) can be found as the
solutions of the two established linear equations. Sub-
stitution of the obtained values in equation (7) then
leads to a fully determined expression of the steady-
state pgf U(z) of the system occupancy.
From this result, various performance measures
of practical importance can then be derived. For in-
stance, the mean system occupancy can be found as
E[u] = U
′
(1). By applying (the discrete-time ver-
sion of) Little’s result (Kleinrock, 1975; Bruneel and
Kim, 1993; Fiems and Bruneel, 2002), the mean de-
lay (system time) of a customer can be obtained as
E[d] = U
′
(1)/λ, and so on. In the next subsection,
we treat a special case in which the computations can
be further simplified and explicit closed-form expres-
sions can be obtained for most quantities of interest.
3.3 Special Case: Geometric Arrivals
Let us consider the special case whereby the number
of arrivals per slot has a geometric distribution with
mean value λ. Then, e(n) and E(z) are given by
e(n) =
1
1+ λ

λ
1+ λ

n
, n ≥ 0 ,
E(z) =
1
1+ λ− λz
,
and (7) can be rewritten as
U(z) =
u(0)(z+ 1 − α) + u(1)(1− α)z
−λz
2
+ z+ (1− α)
, (8)
where we have cancelled out a common factor z− 1
from the numerator and the denominator.
It is not difficult to see that, as soon as the stability
condition (6) is satisfied, the (quadratic) denominator
of (8) has two zeroes, one of which (z
1
) is inside the
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
34

unit disk, and one of which (z
0
) is outside the unit
disk. As explained above, the bounded nature ofU(z)
inside the unit disk implies that z
1
should also be a
zero of the numerator of equation (8), which happens
to be a linear function of z. It then follows that U(z)
can be further simplified by cancelling out the com-
mon factor z− z
1
from the numerator and the denom-
inator and using the normalizing condition U(1) = 1.
As a result we obtain
U(z) =
1− z
0
z− z
0
, (9)
where z
0
is given by
z
0
=
1+
p
1+ 4λ(1− α)
2λ
. (10)
The pgf U(z) given in equation (9) can be eas-
ily inverted; the correspondingpmf of the steady-state
system occupancy reads
u(i) =

1−
1
z
0

1
z
0

i
, i ≥ 0 , (11)
i.e., the system occupancy has a geometric distribu-
tion with parameter 1/z
0
. The tail distribution
Prob[u > i], i.e., the probability that more than i cus-
tomers be present in the system — which can be
used as a rough approximation for the loss proba-
bility in a finite-capacity system with room for ex-
actly i customers, see (Steyaert and Bruneel, 1995;
Gouweleeuw and Tijms, 1998; Kim and Schroff,
2001) — can be expressed as
Prob[u > i] =

1
z
0

i+1
, i ≥ 0 . (12)
The mean system occupancy E[u] at the beginning
of an arbitrary slot can be easily derived as well:
E[u] =
1
z
0
− 1
=
1− 2λ −
p
1+ 4λ(1− α)
2(λ− 2+ α)
. (13)
Finally, the mean delay E[d] of a customer (ex-
pressed in time slots) can be obtained from the
discrete-time version of Little’s result (Bruneel and
Kim, 1993; Fiems and Bruneel, 2002):
E[d] =
E[u]
λ
=
1− 2λ −
p
1+ 4λ(1− α)
2λ(λ − 2+ α)
. (14)
It is worth noting that the stability condition (6)
is clearly reflected in the expressions (13) and (14),
in that the denominators of both expressions tend to
zero as the mean arrival rate λ approaches its limit-
ing value 2− α, indicating the unbounded growth of
(mean) buffer occupancy and delay as the system ap-
proaches the border of its stability region.
4 DISCUSSION OF RESULTS AND
NUMERICAL EXAMPLES
In this section, we discuss the results obtained in the
previous section, both from a qualitative perspective
and by means of some numerical examples.
The first interesting result obtained is the form of
the stability condition (6),
λ < 2− α ,
which shows that the maximum achievable through-
put of this system, expressed in customers per slot, is
very directly determined by the degree of class clus-
tering in the arrival process as described by the clus-
ter parameter α. For this specific model, the formula
is remarkably simple and shows that the achievable
throughput decreases linearly with the cluster param-
eter α. As α can take values between 0 and 1, the
maximum throughput can vary between (nearly) 2
customers per slot and (nearly) 1 customer per slot.
It is interesting to look at the extreme values α = 0
and α = 1. If the cluster parameter is equal to zero,
then the types of two consecutive customers are al-
ways opposite, and one type of customers can never
block the other type; in this case both servers A and B
are active as soon as at least two customers are present
in the system, i.e., the system is work-conserving and
behaves as a regular queue with two identical servers
able to serve all customers. However, as soon as some
amount of “class clustering” appears in the arrival
stream, the achievable throughput is affected, accord-
ing to equation (6). In the extreme case where the
cluster parameter is equal to 1, all customers belong
to the same class and only one of the two servers is
actually being used by the arrival stream; in this case,
the system behaves as a single-server queue and the
throughput can never exceed 1 customer per slot.
These results show that the presence of “class
clustering” in the arrival stream of a multiclass queue
with dedicated servers and “global FCFS” service
discipline can actually be devastating for the perfor-
mance of the queue, and we believe that this phe-
nomenon has been largely overlooked in the regular
queueing literature. Another way of looking at this
phenomenon is to rewrite the inequality (6) as
λ+ α < 2 , (15)
which seems to say that the actual traffic intensity (λ)
and the cluster parameter (α) are equally important
with respect to the stability of the queue: you can
afford more load only if you can decrease the class
clustering of the arrival stream, i.e., the class cluster-
ing appears to represent some kind of additional or
virtual load to the system. In this sense, the quantity
IMPACT OF BLOCKING WHEN CUSTOMERS OF DIFFERENT CLASSES ARE ACCOMMODATED IN ONE
COMMON QUEUE
35

0
10
20
E[u]
0 1 2
λ
α = 0
α = 0.25
α = 0.5
α = 0.75
α = 1
Figure 2: Mean system contents versus the mean arrival rate
for various values of the cluster parameter.
0
10
20
E[u]
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
α
λ = 0.5
λ = 1
λ = 1.5
Figure 3: Mean system contents versus the cluster parame-
ter for various values of the mean arrival rate.
λ+ α could be considered as some kind of equivalent
traffic intensity of the system.
For the case of geometric arrivals, as discussed in
subsection 3.3, we show some numerical results in
figures 2− 4.
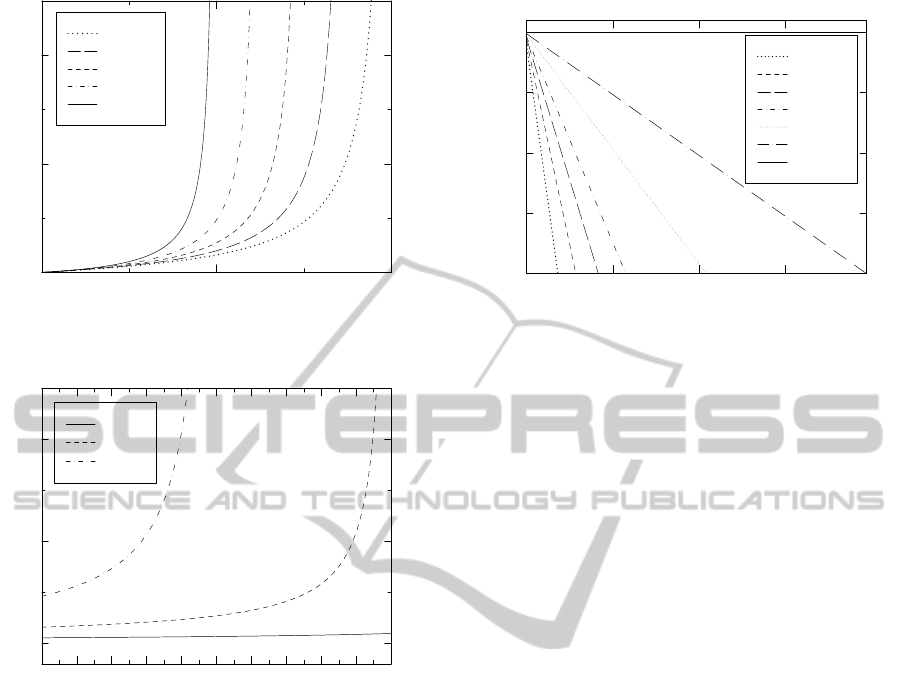
Fig. 2 shows the mean system contents E[u] ver-
sus the mean arrival rate λ, for various values of the
cluster parameter α. The figure clearly illustrates the
great and direct (negative) impact of “class cluster-
ing” on the average number of customers in the sys-
tem, for any givenarrival intensity lower than 1. More
generally, it also shows the shrinking stability region
of the system, as the degree of class clustering in-
creases. We note that the value α = 0.5 represents
the case where the types of consecutive customers in
the arrival stream are independent. Our results prove
that neglecting the correlation between the types of
consecutive customers may lead to either serious un-
derestimation or overestimation of the mean system
occupancy.
In Fig. 3, we have plotted the mean system con-
λ = 1
10
−1
10
−2
10
−3
10
−4
10
0
P rob[u > i]
0 50 100 150
i
α = 0
α = 0.5
α = 0.7
α = 0.8
α = 0.9
α = 0.95
α = 1
Figure 4: Tail probability of the system contents for a given
arrival rate of 1 and various values of the cluster parameter.
tents E[u] versus the cluster parameter α, for given
values of the arrival rate λ. The figure shows that for
lightly loaded systems (e.g. λ = 0.5 in the figure) the
influence of class clustering is negligible. This is also
intuitively clear: the demand of the arrival stream, in
such a case, is considerably less than the traffic that
can be handled by 1 server, and therefore, the question
of whether the second server is also active or not —
which is determined by the amount of class clustering
— is not very relevant. However, as soon as the ar-
rival rate λ exceeds the value 1, the cluster parameter
α becomes important. Specifically, the average queue
size can even grow without bound when α reaches the
value 2− λ.
Fig. 4 shows the tail probability Prob[u > i],
which can be considered as an approximate value for
the loss probability in a system with finite storage ca-
pacity equal to i places, versus the value of i, for a
given value λ = 1 and various values of the cluster pa-
rameter α. The results in this figure can be used, for
instance, for dimensioning purposes of the required
buffer size to achieve a prescribed loss ratio. As an
example, let us assume a target loss ratio of 10
−4
,
then the graphs in Fig. 4 show that the required buffer
size depends very strongly on the cluster parameter
α: for α = 0, a storage capacity of 18 is sufficient;
α = 0.5,0.7, 0.8,0.9 and 0.95 require a buffer size of
29, 42, 58, 105, 197 respectively, whereas for α = 1
the system is unstable and a loss ratio of 10
−4
is not
even achievable.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, we have developed a queueing model
that enables to evaluate scenarios where customers
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
36

requiring different service types, each provided by
distinct servers, are accommodated in one common
queue. We have proposed a dual-class, two-server
queueing model with class-dedicated servers in dis-
crete time, operating under the global FCFS service
discipline, assuming independent arrivals from slot to
slot with a simple first-order Markovian class cluster-
ing model. The model is relatively simple so as to
allow for an analytical solution, but yet contains all
the important elements needed for a conceptual study
of the effect of “global FCFS” on this type of queue.
We emphasize that we have succeeded in deriving an
explicit formula for the pgf of the system occupancy,
under general assumptions with respect to the arrival
statistics. For the special case of geometric arrivals,
we have even been able to obtain explicit closed-form
expressions for the pmf’s, the mean values and the tail
distributions of system occupancy. The results reveal
the very direct and great influence of the degree of
“class clustering” in the arrival stream on the stability
and the performance of the system. We believe that
this is the main qualitative conclusion of the study.
In general, only few studies have focused on the
phenomenon of class clustering in the context of mul-
ticlass queueing systems, and this paper shows that
the effect of class clustering may be very impor-
tant, possibly not only in queues with class-dependent
servers and global FCFS, but also in other queueing
situations whereby the service mechanism is sensi-
tive to the order of service of customers of different
classes. For instance, we expect that class clustering
may also have substantial effects on the performance
of priority queues or queues whereby the lengths of
the service times depend on the way customers of dif-
ferent types succeed each other.
The model examined in this paper can be gen-
eralized in various directions. To start with, more
general service-time distributions can be considered
than the simple deterministic one-slot-per-customer
model studied in this paper. The extra difficulty is
that two customers of different types do not necessar-
ily leave the system in order of their arrival anymore,
exactly due to the variable service times. We note
that the simplest model in continuous time with ex-
ponential service times already has this difficulty (see
e.g. (M´elange et al., 2011)). Also, the assumption
of independent arrivals from slot to slot may be re-
laxed to allow for correlated or bursty types of arrival
processes. Depending on the precise details of the
class clustering model used, this may also affect the
performance of the system considerably. Finally, we
may consider more complicated models for the class
clustering mechanism than the simple one-parameter
model used in this paper. As already touched upon
in section 2, the current study is restricted to systems
whereby both customer classes are equiprobable and
the probability of having a next customer of the same
(or opposite) type as the previous one does not de-
pend on the type of the previous customer. Many dif-
ferent types of more general models than this can be
envisaged. For instance, the types of consecutive cus-
tomers in the arrival stream could be modeled as a
two-state Markov chain with general transition prob-
abilities, or the sizes of subsequent clusters of cus-
tomers of each type could be described by general
(rather than geometric) probability distributions, and
so on. We plan to tackle several of these generaliza-
tions in future work.
REFERENCES
Beekhuizen, P. and Resing, J. (2009). Performance analysis
of small non-uniform packet switches. Performance
Evaluation, 66:640–659.
Bruneel, H. and Kim, B. (1993). Discrete-time models for
communication systems including ATM. Kluwer Aca-
demic, Boston, USA.
Fiems, D. and Bruneel, H. (2002). A note on the discretiza-
tion of Little’s result. Operations Research Letters,
30:17–18.
Gonz´ales, M. (1992). Classical complex analysis. Marcel
Dekker, New York, USA.
Gouweleeuw, F. and Tijms, H. (1998). Computing loss
probabilities in discrete-time queues. Operations Re-
search, 46:149–154.
Karol, M., Hluchyj, M., and Morgan, S. (1987). Input ver-
sus output queueing on a space-division packet switch.
IEEE Transactions on Communications, 35:1347–
1356.
Kim, H. and Schroff, N. (2001). Loss probability calcu-
lations and asymptotic analysis for finite buffer mul-
tiplexers. IEEE/ACM Trans. on Networking, 9:755–
768.
Kleinrock, L. (1975). Queueing systems, part I. Wiley, New
York, USA.
Laevens, K. (1999). A processor-sharing model for input-
buffered ATM-switches in a correlated traffic environ-
ment. Microprocessors and Microsystems, 22:589–
596.
Liew, S. (1994). Performance of various input-buffered and
output-buffered ATM switch design principles under
bursty traffic: simulation study. IEEE Transactions on
Communications, 42:1371–1379.
Mandelbaum, A. and Reiman, M. (1998). On pooling in
queueing networks. Management Science, 44:971–
981.
M´elange, W., Bruneel, H., Steyaert, B., and Walraevens, J.
(2011). A two-class continuous-time queueing model
with dedicated servers and global fcfs service disci-
pline. In Analytical and Stochastic Modeling Tech-
niques and Applications, volume 6751 of Lecture
IMPACT OF BLOCKING WHEN CUSTOMERS OF DIFFERENT CLASSES ARE ACCOMMODATED IN ONE
COMMON QUEUE
37

Notes in Computer Science, pages 14–27. Springer
Berlin / Heidelberg.
Ngoduy, D. (2006). Derivation of continuum traffic model
for weaving sections on freeways. Transportmetrica,
2:199–222.
Nishi, R., Miki, H., Tomoeda, A., and Nishinari, K. (2009).
Achievement of alternative configurations of vehicles
on multiple lanes. Physical Review E, 79:066119.
Steyaert, B. and Bruneel, H. (1995). Accurate approxima-
tion of the cell loss ratio in ATM buffers with multi-
ple servers, volume 1 of Performance Modelling and
Evaluation of ATM Networks, pages 285–296. Chap-
man & Hall, London.
Stolyar, A. (2004). MaxWeight scheduling in a generalized
switch: state space collapse and workload minimiza-
tion in heavy traffic. Annals of Applied Probability,
14:1–53.
Van Dijk, N. and Van der Sluis, E. (2008). To pool or not
to pool in call centers. Production and Operations
Management, 17:1–10.
Van Woensel, T. and Vandaele, N. (2006). Empirical vali-
dation of a queueing approach to uninterrupted traffic
flows. 4OR, A Quarterly Journal of Operations Re-
search, 4:59–72.
Van Woensel, T. and Vandaele, N. (2007). Modeling traffic
flows with queueing models: A review. Asia-Pacific
Journal of Operational Research, 24:435–461.
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
38