THE PRIZE-COLLECTING VEHICLE ROUTING PROBLEM WITH

NON-LINEAR COST

Integration of Subcontractors into Route Design of Small Package Shippers

Andreas Stenger

IT-based Logistics, Goethe University Frankfurt, Grueneburgplatz 1, 60323 Frankfurt, Germany

Keywords:

Vehicle routing, Prize-collecting, Subcontracting, Heuristic.

Abstract:

In this paper, we propose a new routing problem to model a highly relevant planning problem in small package

shipping. The problem, called Prize-Collecting Vehicle Routing Problem with Non-Linear cost (PCVRPNL),

allows for each customer the choice of being serviced by a vehicle of the private ﬂeet or being outsourced to

a subcontractor. A lower bound on the total customer demand serviced by the private ﬂeet ensures a constant

capacity utilization. The subcontracting costs follow a non-linear function representing the discount given

by a subcontractor if larger amounts of packages are assigned. To solve the NP-hard problem, we propose a

Variable Neighborhood Search algorithm. In numerical studies performed on benchmark instances adapted

from classical VRP, we demonstrate the strong performance of our algorithm and study the effect of different

cost functions on the routing solution.

1 INTRODUCTION

The market of small package shippers (SPS) drasti-

cally changed since the deregulation in EU as well as

in USA. The formerly big players like DHL

operated

a huge ﬂeet of vehicles and performed all last-mile

deliveries by their own employees. However, rising

competition forces them to adapt the business model

of companies like DPD

, that use subcontractors for

the last-mile deliveries. Instead of high ﬁxed costs in-

curred by vehicles or employees, they pay subcontrac-

tors per parcel delivered. Beside outsourcing of whole

delivery areas, subcontractors are often used on the

operational level to balance high demand ﬂuctuations,

in particular when the capacity of the owned vehicles

is not sufﬁcient to serve all customers on a given day.

On these days, the problem is to decide which cus-

tomers should be served by an own driver and which

customers should be subcontracted. Thus, a trade-off

between routing costs based on the solution of a Ve-

hicle Routing Problem (VRP) and the ﬁxed costs for

subcontracting a customer have to be made. (Chu,

2005) modeled this planning problem, relaxing sev-

eral practical constraints, as an extension of the clas-

sical VRP, which was later named VRP with Private

www.dhl.com

www.dpd.com

Fleet and Common carriers (VRPPC) (Bolduc et al.,

2008).

However, the VRPPC disregards important real-

world characteristics. First, a lower bound of cus-

tomer served by the private ﬂeet is mandatory in order

to maintain the proﬁtability of the vehicle ﬂeet. Sec-

ond, the costs charged by the subcontractor for serv-

ing an additional customer follow a non-linear cost

function, since the subcontractor itself tries to opti-

mize its capacity utilization.

In this paper, we contribute by modeling the real-

world planning task as a Prize-Collecting Vehicle

Routing Problem with Non-Linear costs (PCVRPNL)

extending the well-known Prize-Collecting Traveling

Salesman Problem (PCTSP). In a PCTSP, a prize is

collected when visiting a customer and penalty costs

incur for each unvisited customer. An additional con-

straint requires to collect at least a given prize. The

objective is to minimize the sum of distances traveled

and penalty costs for unvisited customers. In our case,

penalty cost are equal to subcontracting cost while at

least a given customers demand (prize) have to be ser-

viced by the private ﬂeet. We generate a set of test in-

stances which we solve by means of a Variable Neigh-

borhood Search (VNS) algorithm. Furthermore, we

study the effect of different cost functions on the route

design and the subcontracting decisions as well as the

inﬂuence of the lower bound chosen for the customer

265

Stenger A..

THE PRIZE-COLLECTING VEHICLE ROUTING PROBLEM WITH NON-LINEAR COST - Integration of Subcontractors into Route Design of Small

Package Shippers.

DOI: 10.5220/0003740002650273

In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 265-273

ISBN: 978-989-8425-97-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

assignment.

The remainder of our paper is structured as fol-

lows. In Section 2, we brieﬂy review the literature

related to our work. Subsequently, we formulate the

PCVRP as an Integer Linear Program (ILP) in Section

3. The proposed VNS solution method is detailed in

Section 4. In Section 5, we present the computational

studies performed followed by some concluding re-

marks in Section 6.

2 LITERATURE REVIEW

In this section, we provide a brief review of literature

on PCTSP and VRPPC which are of importance for

our work.

The idea of prize-collecting ﬁrst arised in the con-

text of the iron and steel industry. There, a PCTSP

was used to model the operational scheduling of a

steel rolling mill. (Balas, 1989) transferred this idea

to the general case of a traveling salesman and studied

structural properties. A traveling salesman collects a

prize for each city visited and has to pay a penalty for

each city that remains unvisited. The objective is to

minimize the total distance traveled and penalty costs

incurred for unvisited cities while collecting at least a

given amount of prize money. Several solution meth-

ods are proposed for the PCTSP in literature.

(Dell’Amico et al., 1998) presented a heuristic

that starts from solutions obtained by lagrangian re-

laxation. The subsequent improvement phase applies

an extension and collaborate procedure.

Recently, (Chaves and Lorena, 2008) proposed

a hybrid metaheuristic that generates initial solu-

tions by means of a combined greedy randomized

search procedure and VNS. Based on this, clusters are

formed and promising clusters are identiﬁed in order

to further improve those by a local search procedure.

However, no common benchmark set for PCTSP

exists so that the quality of the various solution meth-

ods proposed can not be evaluated straightforward.

For an extended literature review, we refer the

reader to (Feillet et al., 2005) who provide a classiﬁed

overview of literature on traveling salesman problems

with proﬁts that also include the PCTSP.

In the context of iron and steel industry applica-

tions, (Tang and Wang, 2006) extended the PCTSP to

a prize-collecting vehicle routing problem (PCVRP)

in order to model the scheduling of a hot rolling mill.

Each customer represents an order to be scheduled

which has a given length that corresponds to the de-

mand of the customer. Each vehicle route describes a

turn whereby the vehicle capacity corresponds to the

maximum length of a turn. The objective is to ﬁnd

the optimal schedule so as to minimize the production

costs while proﬁts of orders are considered.

In the context of deliveries from warehouses to lo-

cal customers, (Chu, 2005) proposed a routing model

based on a VRP, in which a customer can either be

served by a truck of the privat ﬂeet or outsourced to

a common carrier. While costs for deliveries per-

formed by a private truck depend on the distances

traveled plus ﬁxed vehicle cost, a common carrier is

paid a ﬁxed price per assigned customer. The ob-

jective is to minimize the total costs incorporating

ﬁxed vehicle costs and variable travel costs of pri-

vate trucks as well as costs of assigning deliveries to

the common carrier. To solve this NP-hard problem

which was later named VRPPC (Bolduc et al., 2008),

(Chu, 2005) presented a simple heuristic based on

the well-known Clarke and Wright algorithm (Clarke

and Wright, 1964). Another simple heuristic that

outperforms the approach of (Chu, 2005) was devel-

oped by (Bolduc et al., 2007). (Bolduc et al., 2008)

modeled the VRPPC as heterogeneous VRP and

proposed a randomized construction-improvement-

perturbation heuristic. Furthermore, they generated

two large sets of benchmark instances for the VRPPC

with up to 480 customers, based on classical VRP

instances. Recently, two tabu search (TS) heuris-

tics have been developed for the VRPPC. (Cˆot´e and

Potvin, 2009) presented a heuristic which is mainly

based on the uniﬁed TS framework proposed by

(Cordeau et al., 1997) (?)see also¿Cordeau:2001. The

solutions obtained by this heuristic were further im-

proved by the TS of (Potvin and Naud, 2011) which

is enhanced by the concept of ejection chains. Nu-

merical studies show that ejection chains helped to

clearly improve the solution quality, in particular on

instances with heterogeneous vehicle ﬂeet, but lead

also to a signiﬁcantly increased computing time.

3 ILP FORMULATION OF THE

PCVRP

Adapting the VRPPC formulation of (Bolduc et al.,

2008), the PCVRPNL can be stated as follows. Given

an undirected graph with a vertex set V = {0...n} and

an arc set A. Vertex 0 denotes the depot and all other

vertices are customers with a demand of q

units. A

customer can either be serviced by a vehicle k of the

set of private vehicles K or by a subcontractor. The

private vehicle ﬂeet consists of m identical vehicles

with restricted capacity Q. For each vehicle used ﬁxed

costs f

are charged as well as variable costs c

for

traversing edge (i, j).

Assigning a customer to a subcontractor incurs

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

266

non-linear cost consisting of a standard price p

which

is discounted by factor (1 − e). The price p

denotes

the cost charged if only customer i is assigned to the

subcontractor and e the discount factor. With growing

total demand delivered by the subcontractor, discount

factor e is increased following a stepwise function in

order to represent the situation in practice. At least L

demand units have to be delivered by the private ﬂeet.

Furthermore, we use the following binary vari-

ables. Variable x

ijk

is equal to 1 if vehicle k uses

edge(i, j), otherwise 0, for i, j ∈ V, i 6= j and k ∈ K.

Variable y

is set to 1 if vehicle k visits node i, oth-

erwise it is equal to 0, for i ∈ V, k ∈ K. The binary

variable z

takes value 1 if customer i is assigned to

a subcontractor, otherwise 0, for i ∈ V\{0}. Finally,

let u

denote an upper bound on the load of vehicle

vehicle k upon leaving customer i for i ∈ V\{0} and

k ∈ K (Bolduc et al., 2008; Cˆot´e and Potvin, 2009).

min

∑

k=1

· y

∑

k=1

∑

i=0

∑

j=0

j6=i

· x

ijk

+ (1 − e) ·

∑

i=1

· z

(1)

∑

k=1

∑

j=1

0jk

∑

k=1

∑

i=1

i0k

≤ m (2)

∑

j=0

j6=h

hjk

∑

i=0

i6=h

ihk

= y

, h ∈ V;k ∈ K (3)

∑

k=1

+ z

= 1, i ∈ V\{0} (4)

∑

i=1

· y

≤ Q, k ∈ K (5)

∑

i=1

∑

k=1

· q

≥ L (6)

− u

+ Q · x

ijk

≤ Q− q

i, j ∈ V\{0};i 6= j;k ∈ K (7)

ijk

∈ {0,1};y

∈ {0,1};z

∈ {0,1} (8)

≥ 0, i ∈ V\{0},k ∈ K (9)

The objective function (1) minimizes the total ex-

penses of the SPS, involving ﬁxed costs for vehicles

used, variable transportation cost as well as subcon-

tracting cost for outsourced customers. The number

of available vehicles of the private ﬂeet is restricted

to m by Constraints (2), while Constraints (3) imply

that a customer vertex i has to be entered and left by

the same vehicle k. Constraints (4) ensure that each

customer is either served by the private ﬂeet or a sub-

contractor. The maximum capacity of a vehicle of the

private ﬂeet is limited to Q by Constraints (5). Con-

straint (6) speciﬁes the minimum customer demand L

to be serviced by the privateﬂeet. Subtour elimination

constraints are given in Constraints (7). Finally, Con-

straints (8) deﬁne the binary nature of variable x

ijk

and z

and Constraints (9) deﬁne the possible val-

ues for u

The model differs from the VRPPC formulation

in the objective function (1), that includes the non-

linear subcontracting cost, and in Constraint (6), that

deﬁnes the minimum “prize” to be collected. In our

case, the prize corresponds to the demand serviced by

the private ﬂeet.

4 SOLUTION METHOD FOR THE

PCVRP

The PCVRPNL is designed to model the real-world

route planning problem of an SPS. Since the prob-

lem is clearly NP-hard, only small instances can be

solved by an exact approach. In order to tackle large

real-world instances, we propose a VNS algorithm.

The algorithm is adapted from the AdaptiveVNS pro-

posed by (Stenger et al., 2011) for the Multi-Depot

VRPPC, where it has shown its high performance in

both solution quality and computing time.

In general, VNS, originally proposed by (Mlade-

novi´c and Hansen, 1997), is a metaheuristic that per-

forms local search on systematically changing, ran-

domly generated neighborhoods. In this way, a high

diversiﬁcation is achieved which helps to efﬁciently

search for improving solutions. VNS is highly popu-

lar especially for tightly constraint and large routing

problems such as VRP with time windows (Br¨aysy,

2003) and large-scale VRP (Kyt¨ojoki et al., 2007).

In Figure 1, we provide a pseudocode of the basic

VNS algorithm as proposed by (Hansen and Mlade-

novi´c, 2001). In the initialization phase, a set of κ

neighborhood structures N

has to be deﬁned. After

ﬁnding an initial solution x the algorithm proceeds to

the shaking phase which is repeated until a stopping

criterion is met. In the shaking, starting from initial

solution x, a ﬁrst neighboring solution x

′

is randomly

generated by using the neighborhood structure κ = 1.

Subsequently, a greedy local search is performed on

′

to determine the local minimum x

′′

. If the solution

′′

improves on the incumbent solution x, we replace

x by x

′′

and the shaking procedure restarts with x

′′

initial solution and neighborhood structure κ = 1. In

case x

′′

is worse than the initial solution x, the shak-

ing proceeds with x as starting point and uses now the

more distant neighborhood structure κ + 1. Typical

stopping criterions are a ﬁxed number of iterations or

number of iterations without improvement.

THE PRIZE-COLLECTING VEHICLE ROUTING PROBLEM WITH NON-LINEAR COST - Integration of

Subcontractors into Route Design of Small Package Shippers

267

1: {Initialization}

2: Deﬁne neighborhood structures N

with κ ∈ [1,..,κ

max

]

3: Find initial solution x

4: Set κ := 1

5: repeat

6: {Shaking}

7: Generate randomly x

′

∈ N

(x)

8: {Local Search}

9: Find local optimum x

′′

with local search algorithm

starting from initial solution x

′

10: {Acceptance Decision}

11: if x

′′

improves x then

12: x ← x

′′

13: κ ← 1

14: else

15: κ ← κ+ 1

16: end if

17: until κ = κ

max

Figure 1: Pseudocode of the basic VNS algorithm as pro-

posed by (Mladenovi´c and Hansen, 1997).

In the following, we provide the algorithmic de-

tails of the initialization, shaking and local search

phases used in our VNS algorithm designed for the

PCVRPNL.

4.1 Initialization

The aim of the initialization phase is to quickly com-

pute a ﬁrst feasible solution which serves as starting

point for the shaking phase. In detail, we need ﬁrst to

assign all customers either to the private ﬂeet or the

subcontractor and second to determine vehicle routes

for the private ﬂeet.

Our approach is a modiﬁed version of the initial-

ization method proposed by (Cˆot´e and Potvin, 2009)

for the closely related VRPPC. In general, the idea

is to service not more than the mandatory demand L

by the private ﬂeet and to subcontract all remaining

customers. In order to identify the most suitable cus-

tomers to be subcontracted, we start by ordering all

customers according to the quotient p

in increas-

ing order, where p

denotes the subcontracting cost

of customer i and q

the demand. Subsequently, we

assign the ﬁrst b customers to the subcontractor with

∑

i=1

≥

∑

i=1

− L ≥

b−1

∑

i=1

(10)

where L denotes the minimum customer demand to

be service by the private ﬂeet (see Section 3). The

remaining customers are assigned to the private ﬂeet

and initial vehicle routes are constructed by means of

the well-known Clarke and Wright algorithm (Clarke

and Wright, 1964). The routing is further improved

by a greedy local search that uses the neighborhoods

described in Section 4.3.

4.2 Shaking

Starting from an initial solution, the shaking proce-

dure randomly generates neighboring solutions based

on predeﬁned neighborhood structures. We deﬁne

our neighborhood structures by means of a move-

exchange and a cyclic-exchange operator (Thompson

and Psaraftis, 1993). In both cases, we separate those

neighborhoodsthat only consider routes of the private

ﬂeet and those that allow the exchange between routes

of the private ﬂeet and the subcontractor. In detail, we

use the following neighborhood structures.

• Moving a sequence of customers among vehicle

routes of the private ﬂeet: The ﬁrst six neighbor-

hood structures (κ = 1,..., 6) move a sequence of

ω customers from one route into another. The se-

quence length ω to be exchanged on neighbor-

hood κ is randomly selected as min([0,κ], |N|),

where |N| denotes the number of customers in the

route.

• Moving a sequence of customers among vehi-

cle routes of the private ﬂeet and subcontrac-

tor: The following six neighborhood structures

(κ = 7, ...,12) are similar to the ﬁrst set, however,

customer sequences can additionally be inserted

into or removed from the subcontractor.

• Exchanging customer sequences among vehicle

routes of the private ﬂeet: This set of neighbor-

hood structures transfers sequences of up to 6 cus-

tomers among up to 4 routes in a cyclic way. Con-

sidering an example with three routes, a customer

sequence is removed from route r

and inserted

into route r

where a sequence of customers is

extracted and moved to route r

. The sequence

removed from route r

is ﬁnally inserted into r

which closes the circle of exchange. Neighbor-

hood structures κ = 13,...,18 consider exchanges

among 2 routes, κ = 19,..., 24 exchanges among

3 routes and neighborhood structures κ = 25,...30

involve exchanges of up to 4 routes. The maxi-

mum sequence length to be exchanged increases

for each subset with increasing κ and the actual

length to be exchanged ω is randomly selected as

described in the ﬁrst set.

• Exchanging customer sequences among vehicle

routes of the private ﬂeet and the subcontractor

This set of 18 neighborhood structures is similar

to the third set but involves again not only vehicle

routes of the private ﬂeet but also the subcontrac-

tor.

4.3 Local Search

Routes modiﬁed during the shaking phase are opti-

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

268

mized by a greedy local search to determine the local

optimum. On the single route level, we use the well-

known edge-exchange operators 2-opt and Or-opt. 2-

opt replaces two existing edges by two new ones (Lin,

1965) while Or-opt similarly substitutes three non-

consecutive edges without inverting any of the route

segments (Or, 1976). Considering exchanges among

different routes, we apply the relocate-exchange as

well as the swap-operator. In a relocate move, a single

customer is extracted from one route and inserted at

the cost-optimal position in another one. Given cus-

tomer a in route r

and customer b in route r

, the

swap-operator inserts customer b in r

at the former

position of a and customer a into r

at the former po-

sition of b.

In order to efﬁciently explore the solution space,

infeasible solutions are accepted during the search by

means of a penalty mechanism. In the case of the

PCVRPNL, a solution can be infeasible in terms of

violating capacity limits of vehicles and falling below

the minimum demand to be serviced by the private

ﬂeet. Any violation is penalized by adding a penalty

term to the objective function. Let OverCap de-

note the overcapacity and LowPrize the demand units

required to satisfy the typical prize-collecting con-

straints. If a solution s is infeasible, we add to the ob-

jective function value c(s) a penalty term as follows:

f(s) = c(s) + α · OverCap + β · LowPrize. The vari-

ables α and β describe the penalty factors which are

positive weights in the interval [Pen

min

,Pen

max

]. Ini-

tialized with a value Pen

init

, we update these weights

after each iteration without violation (with violation)

of constraints by dividing (multiplying) by 1.5.

4.4 Acceptance Decision

The solution x

′′

obtained in the local search is com-

pared to the current best solution x and accepted ac-

cording to a given criterion. In standard VNS ap-

proaches, only improving solutions are accepted. Re-

cent works, however, show the high efﬁciency of us-

ing an acceptance criterion inspired by simulated an-

nealing (Hemmelmayr et al., 2009). In this case,

we still accept each move that improves the incum-

bent solution and additionally deterioating moves ac-

cording to the Metropolis probability. Let f(·) be

the objective function value and θ the temperature,

the probability of accepting solution x

′′

is equal to

−(C(x

′′

)−C(x))

. The temperature parameter controls the

degree of the diversiﬁcation achieved by accepting

worse solutions. Starting with an initial value θ

init

0, we constantly reduce the value by factor θ

dec

af-

ter each VNS iteration. In this way, the probability of

accepting a worsening solution decreases during the

search leading to an intensiﬁcation phase at the end in

which all non-improving solutions are rejected.

5 COMPUTATIONAL STUDIES

We coded our VNS algorithm in Java and run all

tests as single thread on a standard personal computer

equipped with an Intel Core i5 Processor with 2.67

GHz and 4 GB RAM. Since the PCVRPNL is a new

problem class, we designed a set of benchmark in-

stances based on classical VRP ones which we use

for our numerical testings (Section 5.1). To study the

inﬂuence of the non-linear cost function on the sub-

contracting decision, we performed tests with differ-

ent cost functions, which we present in Section 5.2.

In Section 5.3, we analyze how the value of the mini-

mum demand to be delivered by the private ﬂeet inﬂu-

ences the overall solution. The general performance

of our VNS heuristic on related problems, such as

VRPPC, has already been proven in (Stenger et al.,

2011).

5.1 Benchmark Instances

The PCVRPNL is an extension of the classical VRP.

For this reason, we select the classical VRP instances

proposed by (Christoﬁdes and Eilon, 1969) as basis

for designing a new PCVRPNL benchmark set. The

benchmark design is inspired by the VRPPC instances

described in (Bolduc et al., 2008). Note that using the

VRPPC instances is not appropriate since the subcon-

tracting costs used there mainly depend on the cus-

tomers’ distance to the depot. In real-world small

package shipping, costs charged by a subcontractor

are, however, based on the demand of the customers.

The 14 newly designed instances consider up to

199 customers and are thus sufﬁciently large for our

studies. In detail, we keep the depot and customer

coordinates, the customer demand values as well as

the vehicle capacities of the original instances. We

add ﬁxed vehicle cost f

which are highly relevant

for subcontracting decisions and computed the

standard subcontracting price p

for each customer.

Let C(x

∗

) be the objective function value and k

∗

denote the number of vehicles required of a very

good solution to the classical VRP instance (avail-

able on http://neumann.hec.ca/chairedistributique/

data/vrp/old/). The ﬁxed usage cost of a vehicle k

is then computed as f

C(x

∗

)

∗

rounded down to the

nearest integer. The standard subcontracting price

of customer i is calculated as p

= q

( f

·k

∗

)+C(x

∗

)

˜q

where q

denotes the demand of customer i and

THE PRIZE-COLLECTING VEHICLE ROUTING PROBLEM WITH NON-LINEAR COST - Integration of

Subcontractors into Route Design of Small Package Shippers

269

˜q =

∑

i=1

the total demand of all customers of

the speciﬁc instance. Furthermore, we restrict the

number of vehicles available at the depot to k

∗

and set

the minimum demand to be served by the private ﬂeet

L to 0.7˜q. Finally, we compute a simple upper bound

(UB) for our benchmark instances by adding the

vehicle ﬁxed cost, calculated as described above, to

the current best known solution of the corresponding

VRP instance published in (Vidal et al., 2011).

In a preliminary testing on the benchmark set, we

identiﬁed the following parameter setting as the best

compromise between solution quality and computing

time. We start with an initial temperature of θ

init

= 50

and decrease it after each iteration by θ

dec

= 0.05%.

Furthermore, we reset the temperature to θ

init

every

time we performed 200 iterations without improve-

ment in order to force diversiﬁcation. The penalty

factors OverCap and LowPrize are assigned an initial

value Pen

init

= 100 which is varied during the search

between Pen

min

= 1 and Pen

max

= 10000. We stop the

search after 1500 iterations without improvement.

5.2 Cost Functions

In industry practice, a subcontractor is mainly paid

per package volume, i.e. demand unit, which an SPS

assigned to him. However, the price per demand unit

is usually not ﬁxed but depends on the total subcon-

tracted demand. Subcontractors especially give dis-

counts if the demand to be delivered for an SPS ﬁlls

a whole vehicle. In that case, the delivery opera-

tions are most efﬁcient. This fact is represented by

the common stepwise discount function of a subcon-

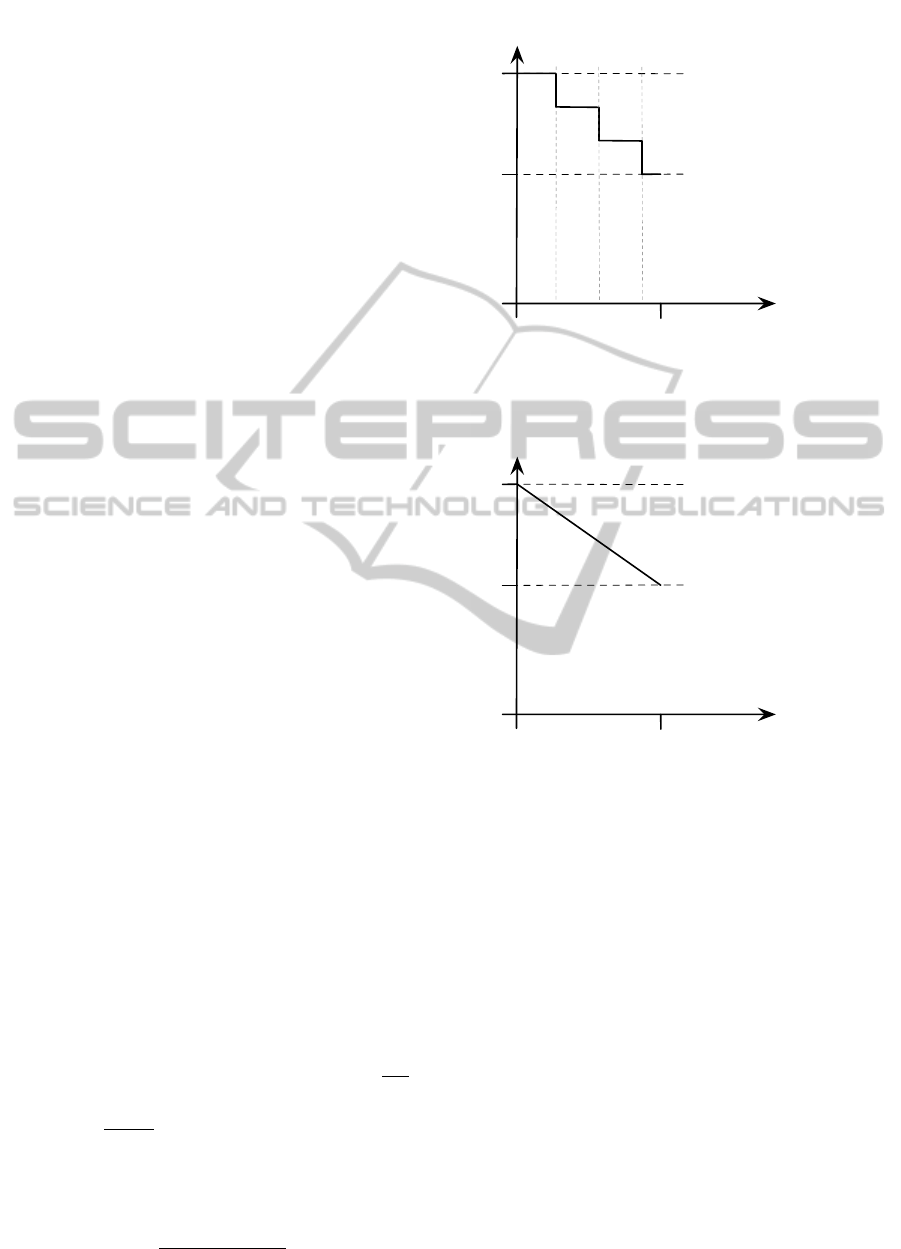
tractor which is depicted in Figure 2 tailored to our

PCVRPNL model. Given the standard price p

repre-

senting costs for solely subcontracting customer i, i.e.

discount factor e

min

= 0, the value of e is increased

every time the total demand assigned to the subcon-

tractor q

current

exceeds 80% of the vehicle capacity

Q. The discount factor e is limited to e

max

= 0.4,

i.e. a subcontractor gives at most a discount of 40%

with respect to the standard price. In our instances,

we link the discount factor e to the minimum de-

mand to be delivered by the private ﬂeet L, such that

e reaches its maximum value at latest when the sub-

contracted demand is equal to ˜q − L. In detail, we

calculated the number of discount steps by ρ =

˜q−L

rounded to the nearest integer. Factor e is hence in-

creased by γ ·

(1−0.6)

, with γ ∈ [1,ρ], if the subcon-

tracted demand exceeds ((γ − 1) + 0.8) · Q demand

units. In order to evaluate the effect of the stepwise

discount function, we additionally performed tests

on the benchmark instances with a linear discount

function (1− e

min

(1−e

max

)−(1−e

min

)

˜q−L

·q

current

, where

0.6

0.8Q 1.8Q 2.8Q

q-L

Cost Factor

(1-e)

Subcontracted

Demand q

current

Figure 2: Stepwise discount function.

0.6

Cost Factor

(1-e)

q-L

~ Subcontracted

Demand q

current

Figure 3: Linear discount function.

current

denotes the currently subcontracted demand

(see Figure 3).

The results obtained with both discount functions

are reported in Table 1. In detail, we publish the best

solution found in 10 runs (Cost), the average comput-

ing time in seconds (CPU) and the average number of

subcontracted customers (|SC|). In addition, we com-

pare our solutions to the upper bound (UB) which is

computed as explained above.

For both discount functions, our solutions found

improve the VRP-based upper bound by more than

20% while requiring moderate computing times.

Since the value of the UB corresponds to the best

known solution of the speciﬁc instance without sub-

contracting, the impressive results show that our algo-

rithm is clearly able to identify those customers that

can be proﬁtably subcontracted and to determine ve-

hicle routes at minimal cost. Comparing the solutions

obtained with the two different discount functions, the

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

270

Table 1: Results obtained on the benchmark instances for the PCVRPNL with a linear and a stepwise discount function.

The upper bound (UB) indicates the best known solution to the corresponding VRP instance, i.e., without subcontracting any

customer.

Linear Stepwise

Instance UB Cost GapUB CPU |SC| Cost GapUB CPU |SC|

CEP-01 1044.61 908.13 -13.07% 40.6 20.2 887.64 -15.03% 44.1 16

CEP-02 1660.26 1385.07 -16.58% 35.8 26.8 1356.62 -18.29% 49.5 20

CEP-03 1650.14 1354.51 -17.92% 145.2 41.8 1332.91 -19.22% 147.9 36

CEP-04 2048.42 1645.06 -19.69% 308.3 57.5 1608.23 -21.49% 294.6 51

CEP-05 2583.45 2141.27 -17.12% 340.2 70.5 2088.79 -19.15% 364.9 63.3

CEP-06 1107.43 872.48 -21.22% 37.0 20.5 846.71 -23.54% 46.4 15

CEP-07 1811.68 1466.35 -19.06% 37.6 27.2 1430.94 -21.02% 50.0 19.9

CEP-08 1729.94 1326.69 -23.31% 147.2 42.1 1306.56 -24.47% 168.1 35.5

CEP-09 2324.55 1734.84 -25.37% 440.5 50.8 1665.60 -28.35% 463.6 58.4

CEP-10 2781.85 2159.32 -22.38% 419.6 70.3 2127.98 -23.50% 312.5 63

CEP-11 2078.11 1792.83 -13.73% 305.8 30.7 1727.17 -16.89% 353.5 37.2

CEP-12 1629.56 1384.45 -15.04% 112.3 32.7 1359.10 -16.60% 120.9 26.2

CEP-13 3081.14 1881.07 -38.95% 432.4 37.8 1838.13 -40.34% 365.2 37

CEP-14 1724.37 1372.29 -20.42% 122.0 30.4 1353.61 -21.50% 104.3 25.6

average 1530.31 -20.27% 208.9 40.0 1495.00 -22.10% 206.1 36.0

gap to the UB of the stepwise discount function is al-

most 10% higher while 10% less customers are sub-

contracted. This can be explained by the fact that

the stepwise function reaches e

max

earlier, i.e. with

less subcontracted demand. In case of the linear func-

tion, increasing the subcontracted demand up to ˜q− L

might be always proﬁtable since the discount factor

continuously increases.

5.3 Varying the Minimum Demand to

be Delivered by the Private Fleet

One of the main characteristics of prize-collecting

problems is the lower bound given to the prize to be

collected or, in our case, the minimum customer de-

mand L which has to be serviced by the private ﬂeet.

Since the value of L strongly inﬂuences the outsourc-

ing decision, we performed tests with different val-

ues of L to quantify the effect on the overall solution

value.

In detail, we solved our benchmark instances us-

ing the standard subcontracting price p

without any

discount function, which is hence a PCVRP. The

value of L is varied between 0.5˜q and 0.9 ˜q while we

solved each instance 10 times with each value. Figure

4 depicts the average gap of the best solutions found

to the upper bound as well as the average number of

subcontracted customers for each value of

˜q

With increasing value of

˜q

and hence limited ﬂex-

ibility of the algorithm, the solution quality clearly de-

creases. Similarly, the number of subcontracted cus-

tomers decreases when the minimum demand to be

serviced by the private ﬂeet is increased. Comparing

the results obtained with

˜q

= 0.5 and 0.9, the num-

ber of subcontracted customers is decreased by almost

75% and the gap to the lower bound is 26% worse.

Although the ﬁndings of this study seem obvious, the

results quantify the strong inﬂuence of the important

real-world constraint that deﬁnes a lower bound on

the demand serviced by the private ﬂeet. In addition,

the results prove again the high efﬁciency of our al-

gorithm in handling the subcontracting decision while

paying attention to the prize-collecting constraint.

6 CONCLUSIONS

In this paper, we proposed the Prize-Collecting

Vehicle Routing Problem with Non-Linear cost

(PCVRPNL) to model an important route planning

problem arising in small package shipping. The prob-

lem is closely related to the Prize-Collecting Trav-

eling Salesman Problem (PCTSP) and the Vehicle

Routing Problem with Private ﬂeet and Common car-

rier (VRPPC). Given a single depot, a set of cus-

tomers with known demand and a homogeneous ve-

hicle ﬂeet, the task is to ﬁnd the vehicle routes for

the private ﬂeet and to decide which customers to

be outsourced to a subcontractor incurring non-linear

cost depending on the total outsourced demand with

the objective of cost minimization. In order to solve

the NP-hard problem, we presented a Variable Neigh-

borhood Search (VNS) algorithm which has already

proven its high performance on related problems.

For the computational testing, we designed a set of

14 benchmark instances adapting classical VRP in-

stances. Numerical studies performed on the bench-

THE PRIZE-COLLECTING VEHICLE ROUTING PROBLEM WITH NON-LINEAR COST - Integration of

Subcontractors into Route Design of Small Package Shippers

271

0,0

5,0

10,0

15,0

20,0

25,0

30,0 -16,00%

-14,00%

-12,00%

-10,00%

-8,00%

-6,00%

-4,00%

-2,00%

0,00%

40% 50% 60% 70% 80% 90% 100%

Minimum Percentage of Demand

to be Serviced by Private Fleet

Average Number of

Subcontracted Customers

Average Gap to Upper Bound

Gap UB SC Customer

Figure 4: Comparing results obtained with different values of the lower bound L. Results show that reducing L leads to lower

total cost, i.e., to a larger gap to the upper bound and to a larger number of subcontracted customers.

mark instances clearly show that our algorithm is able

to efﬁciently solve the PCVRPNL. Furthermore, our

tests demonstrate the strong inﬂuence of the value

chosen for the minimum demand to be serviced by

the private ﬂeet. In a next step, we aim to test our al-

gorithm on a large-scale benchmark set and to study

the multi-depot version of the problem at hand.

ACKNOWLEDGEMENTS

The author was partially supported by BMBF, Grant

01-S09016B, Germany. Thanks are due to Daniel En-

gel for his help in coding the algorithm.

REFERENCES

Balas, E. (1989). The prize collecting traveling salesman

problem. Networks, 19(6):621–636.

Bolduc, M.-C., Renaud, J., and Boctor, F. (2007). A heuris-

tic for the routing and carrier selection problem. Eu-

ropean Journal of Operational Research, 183(2):926–

932.

Bolduc, M.-C., Renaud, J., Boctor, F., and Laporte, G.

(2008). A perturbation metaheuristic for the vehicle

routing problem with private ﬂeet and common car-

riers. Journal of the Operational Research Society,

59(6):776–787.

Br¨aysy, O. (2003). A reactive variable neighborhood search

for the vehicle routing problem with time windows.

INFORMS Journal on Computing, 15(4):347–368.

Chaves, A. A. and Lorena, L. A. N. (2008). Hybrid meta-

heuristic for the prize collecting travelling salesman

problem. In van Hemert, J. and Cotta, C., editors, Evo-

COP 2008. LNCS, vol. 4972. Springer, Heidelberg.

Christoﬁdes, N. and Eilon, S. (1969). An algorithm for one

vehicle-dispatching problem. Operational Research

Quarterly, 20(3):309–318.

Chu, C.-W. (2005). A heuristic algorithm for the truckload

and less-than-truckload problem. European Journal

of Operational Research, 165(3):657–667.

Clarke, G. and Wright, J. W. (1964). Scheduling of vehicles

from a central depot to a number of delivery points.

Operations Research, 12(4):568–581.

Cordeau, J.-F., Gendreau, M., and Laporte, G. (1997). A

tabu search heuristic for periodic and multi-depot ve-

hicle routing problems. Networks, 30(2):105–119.

Cˆot´e, J.-F. and Potvin, J.-Y. (2009). A tabu search heuristic

for the vehicle routing problem with private ﬂeet and

common carrier. European Journal of Operational

Research, 198(2):464–469.

Dell’Amico, M., Mafﬁoli, F., and Sciomachen, A. (1998). A

lagrangian heuristic for the prize collecting travelling

salesman problem. Annals of Operations Research,

81(0):289–305.

Feillet, D., Dejax, P., and Gendreau, M. (2005). Traveling

salesman problems with proﬁts. Transportation Sci-

ence, 39(2):188–205.

Hansen, P. and Mladenovi´c, N. (2001). Variable neighbor-

hood search: Principles and applications. European

Journal of Operational Research, 130(3):449 – 467.

Hemmelmayr, V. C., Doerner, K. F., and Hartl, R. F. (2009).

A variable neighborhood search heuristic for periodic

routing problems. European Journal of Operational

Research, 195(3):791–802.

Kyt¨ojoki, J., Nuortio, T., Br¨aysy, O., and Gendreau, M.

(2007). An efﬁcient variable neighborhood search

heuristic for very large scale vehicle routing problems.

Computers & Operations Research, 34:2743–2757.

Lin, S. (1965). Computer solutions to the traveling-

salesman problem. Bell System Technical Journal,

44(10):2245–2269.

Mladenovi´c, N. and Hansen, P. (1997). Variable neigh-

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

272

borhood search. Computers & Operations Research,

24(11):1097–1100.

Or, I. (1976). Traveling salesman-type problems and

their relation to the logistics of regional blood bank-

ing. PhD thesis, Department of Industrial Engineering

and Management Sciences, Northwestern University

Evanston, IL.

Potvin, J.-Y. and Naud, M.-A. (2011). Tabu search with

ejection chains for the vehicle routing problem with

private ﬂeet and common carrier. Journal of the Op-

erational Research Society, 62(2):326–336.

Stenger, A., Vigo, D., Enz, S., and Schwind, M. (2011).

An adaptive variable neighborhood search algorithm

for a vehicle routing problem arising in small package

shipping. to appear in: Transportation Science.

Tang, L. and Wang, X. (2006). Iterated local search al-

gorithm based on very large-scale neighborhood for

prize-collecting vehicle routing problem. The Interna-

tional Journal of Advanced Manufacturing Technol-

ogy, 29(11-12):1246–1258.

Thompson, P. M. and Psaraftis, H. N. (1993). Cyclic trans-

fer algorithms for multivehicle routing and scheduling

problems. Operations Research, 41(5):935–946.

Vidal, T., Crainic, T. G., Gendreau, M., Lahrichi, N., and

Rei, W. (2011). A hybrid genetic algorithm for multi-

depot and periodic vehicle routing problems. Techni-

cal report, CIRRELT-2011-05.

THE PRIZE-COLLECTING VEHICLE ROUTING PROBLEM WITH NON-LINEAR COST - Integration of

Subcontractors into Route Design of Small Package Shippers

273