ANALYSIS FOR DISTRIBUTED COOPERATION BASED ON
LINEAR PROGRAMMING METHOD
Toshihiro Matsu and Hiroshi Matsuo
Nagoya Institute of Technology, Gokiso-cho, Showa-ku, Nagoya, 466-8555, Aichi, Japan
Keywords:
Multi-agent, Distributed cooperative problem solving, Linear programming, Optimization.
Abstract:
Distributed cooperative systems have optimization problems in their tasks. Supporting the collaborations of
users, or sharing communications/observations/energy resources, are formalized as optimization problems.
Therefore, distributed optimization methods are important as the basis of distributed cooperation. In partic-
ular, to handle problems whose variables have continuous domains, solvers based on numerical calculation
techniques are important. In a related work, a linear programming method, in which each agent locally per-
forms the simplex method and exchanges the sets of bases, has been proposed. On the other hand, there is
another interest in the cooperative algorithm based on a linear programming method whose steps of processing
are more distributed among agents. In this work, we study the framework of distributed cooperation based on
a distributed linear programming method.
1 INTRODUCTION
Distributed cooperative systems have optimization
problems in their tasks. Supporting the collaborations
of users, or sharing communications/observations/en-
ergy resources, are formalized as optimization prob-
lems. To solve the problems in distributed cooper-
ative processing, understanding the protocols of the
distributed optimization algorithms is important. In
the research area of Distributed Constraint Optimiza-
tion Problems (Modi et al., 2005; Petcu and Faltings,
2005; Mailler and Lesser, 2004), cooperative problem
solving is mainly studied for (non-linear) discrete op-
timization problems. On the other hand, to solve the
problems whose variables have continuous domains,
another type of solvers is also important. Other re-
lated works propose optimization algorithms based on
numericalcalculation techniques for distributed coop-
erative systems (Wei et al., 2010; Burger et al., 2011).
In a related work (Burger et al., 2011), simplex al-
gorithm for linear programming has been applied to
multiagent systems. In the method, each agent lo-
cally performs the simplex method to solve its prob-
lem and exchanges the sets of bases. A good point
of the method is the simple protocol. On the other
hand, there is another interest in the cooperative algo-
rithm based on a linear programming method whose
processing is more distributed among agents. While
there are a number of studies about parallel simplex
methods (e.g. (Ho and Sundarraj, 1994; Yarmish and
Van Slyke, 2009)), their goals are slightly different
from the situation in multiagent cooperation. In this
work, we study a basic framework of distributed co-
operation based on a distributed linear programming
method whose parts are distributed among agents.
The essential distributed processing and extractingthe
parallelism are investigated.
2 PREPARATIONS
2.1 Linear Programming Problems
The linear programming problems are fundamen-
tal optimization problems that consist of n vari-
ables, m linear constraints, a linear objective function
(Chvatal, 1983). For the sake of simplicity, we as-
sume the following problems.
max : c
T
x (1)
subject to Ax = b, x ≥ 0 (2)
Here, n-dimensional vector x consists of decision and
slack variables. Each constraint contains a slack vari-
able. m× n matrix A and m-dimensional vector b re-
spectively represent coefficients and constants of the
constraints. n-dimensional transposed vector c
T
rep-
resents coefficients of the objective function.
228
Matsui T. and Matsuo H..
ANALYSIS FOR DISTRIBUTED COOPERATION BASED ON LINEAR PROGRAMMING METHOD.
DOI: 10.5220/0003750702280233
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 228-233
ISBN: 978-989-8425-96-6
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2.2 Simplex Method
The simplex method is a fundamental solution
method of the linear programming problems(Chvatal,
1983)D In computation of the method, initial bases
are selected. Then the bases are repeatedly improved
until they reach the optimal solution. In the case of the
problems shown in 2.1, slack variables and the objec-
tive value are simply selected as the initial bases. The
objective value must always be a base.
The set of bases is represented by Boolean vector
h. Each element h
j
of h is true if variable x
j
is a
base. Otherwise, h
j
is false. The objective value is
omitted in h because it is always a base. Matrix D is
employed as a table that represents bases, constraints
and an objective function in each step of the solution
method. In the initial state, each element d
i, j
of D
takes the following value.
d
i, j
=





−a
i, j
1 ≤ i ≤ m∧ 1 ≤ j ≤ n
b
i
1 ≤ i ≤ m∧ j = n + 1
c
j
i = m+ 1∧ 1 ≤ j ≤ n
0 i = m+ 1∧ j = n+ 1
(3)
The column for the objective value is omitted similar
to h. Note that d
i,k
for base x
k
takes −1. In the other
row i
′
such that i
′
∈ {1···m}\{i}, d
i
′
,k
is 0. In the
problems shown above, the initial D means that the
slack variables are selected as the initial bases.
2.2.1 Selection of New Base
In the first step of an iteration, the solution method se-
lects one non-base variable x
j
B
that has a positive co-
efficient of the objective function. Then x
j
B
becomes
a new base in the following steps. If all coefficients
of the objective function are not positive, the solu-
tion method stops. In that case, for each i such that
1 ≤ i ≤ m, d
i,n+1
represents the value of the base vari-
able of row i. Also, d
m+1,n+1
represents the optimal
objective value. Here,j
B
is shown as follows.
j
B
= argmax
j
d
m+1, j
(4)
s.t. 1 ≤ j ≤ n ∧ ¬h
j
∧ d
m+1, j
> 0
2.2.2 Selection of New Non-base
Instead of the new base x
j
B
, variable x
j
N
of base vari-
ables is selected as a non-base variable. In the repre-
sentation of D, selecting one row i
N
decides the corre-
sponding base variable. Here, row i
N
that minimizes
the maximum feasible value of x
j
B
is selected.
i
N
= argmin
i
d
i,n+1
−d
i, j
B
(5)
s.t. 1 ≤ i ≤ m∧ d
i, j
B
6= 0∧
d
i,n+1
−d
i, j
B
> 0
j
N
is uniquely determined satisfying the following
condition.
h
j
N
∧ d
i
N
, j
N
= −1 (6)
2.2.3 Exchange of Bases
Now the new base and non-base are exchanged. First,
in D, row i
N
that corresponds to the new base is up-
dated. The new value of each element d
′
i
N
, j
is shown
as follows.
d
′
i
N
, j
=
d
i
N
, j
−d
i
N
, j
B
(1 ≤ j ≤ n + 1) (7)
Then, for each row i excluding i
N
, x
j
B
is eliminated.
Each new value d
′
i, j
is shown as follows.
d
′
i, j
= d
i, j
+ d
i, j
B
d
′
i
N
, j
(8)
(i ∈ {1, · · · , m + 1}\{i
N
}, 1 ≤ j ≤ n + 1)
Here, d
′
i, j
B
is 0 because d
′
i
N
, j
B
= −1. That represents
the elimination of x
j
B
. Additionally, elements of h are
updated as h
j
B
← T, h
j
N
← F. After the exchange of
the bases, the processing is repeated from selecting
the new base.
3 A DISTRIBUTED SOLVER
In this work, we study a framework of distributed co-
operation based on the linear programming problem
and simplex method. Basically, problem and solver
are divided into agents. In the initial state, each agent
knows partial information that is directly related to the
agent. Each agent only updates the initial constraints
and its own coefficient of the objective function in the
solution method. Information that is exchanged be-
tween agents and extraction of parallelism are mainly
investigated. For the simple protocol, we employ a
mediator that manages information.
3.1 Division of Problem
To represent the state of the agent, variable x
j
is re-
lated to agent j. For the sake of simplicity, we assign
agents for slack variables. In the following context, x
j
and j may not be distinguished. In particular, a medi-
ator is represented as z. Based on the variables, initial
D is divided into agents. Agent j knows constraints
that are related to its variable in the initial state. A
constraint is known by multiple agents. j also knows
coefficients of the objective function for known con-
straints. On the other hand, mediator z does not know
any elements of D in the initial state.
Each agent j has table D
j
that contains holes. The
ANALYSIS FOR DISTRIBUTED COOPERATION BASED ON LINEAR PROGRAMMING METHOD
229

notations of D
j
are compatible with D. While D
j
has
the same size as D, its unknown elements are zero. D
z
represents the table of mediator z. Agent j also has
h
j
that partially contains elements of h. In the initial
state, each agent knows whether the variables related
to the known constraints are the base or not. For each
known base or non-base, h
j
is appropriately initial-
ized. Other elements of h
j
are initialized by default
value, false. Additionally, it is assumed that agents
share information about the address of agent z and the
number of all agents.
3.1.1 Selecting New Base
To select new bases, coefficients of the objective func-
tion haveto be comparedfor all non-basevariables. In
the first step, each agent j sends coefficient d
m+1, j
of
x
j
in the objective function to mediator agent z. Ex-
ceptionally, in the case where x
j
is a base or d
m+1, j
<
0, 0 is sent. Additionally, for each non-base variable
x
j
′
that is known by agent j, j computes maximum
value v
⊤
j
′
of x
j
′
in the case where x
j
′
is selected as the
new base. This computation is a part of Equation (5).
Let V
⊤
j
denote a set of v
⊤
j
′
that is computed by j. j
sends V
⊤
j
with d
m+1, j
to mediator z.
Mediator z receives coefficients of the objective
function from all agents whose variable is a non-base.
Also, z receives the maximum values of the variables
from all agents. When all values are received, z se-
lects the candidate of new base x
j
B
. Then z sends a
request to change x
j
B
to a new base. The request and
d
m+1, j
B
are sent to the agent who reported the mini-
mum value of the maximum value v
⊤
j
B
of x
j
B
.
3.1.2 Selecting New Non-base
Selecting the new non-base is performed by agent k
that is requested by mediator agent z. As shown in the
previous subsubsection, agent k receives the request
to change x
j
B
to a new base and d
m+1, j
B
. Then, based
on D
k
, agent k computes row i
N
, which corresponds
to the new non-base in the case where x
j
B
is changed
to the new base.
3.1.3 Exchanging Bases
The exchange of the bases starts from agent k shown
in 3.1.2 and is performed on agents who have part of
D to be updated. In the following, the processing in
agent k and the related agents is shown.
First, k updates an element of h
k
based on D
k
and
h
k
for row i
N
that corresponds to the new non-base.
The Boolean value of h
j
that satisfies the condition
h
j
∧ d
i
N
, j
= −1 shown in Equation (6) is set to false.
By the update, k identifies that x
j
is a new non-base.
Next, k updates D
k
. Row i
N
is previously saved as row
vector d
−
i
N
, and row i
N
is updated as shown in Equa-
tion (7). Then using the updated row i
N
and d
m+1, j
B
that have been received from z, rows of other con-
straints and its own coefficient d
m+1,k
of the objective
function are updated. In particular, if k = j
B
, d
m+1,k
is
0. Other coefficients of the objective function are al-
ways 0, which represents the unknown value. More-
over, k updates the value of h
j
B
in h
k
from false to
true. Now k identifies that x
j
B
is a base.
The update of D
k
has to be sent to agents k
′
whose
D
k
′
is affected by the update. k sends its coefficient
d
m+1,k
of the objective function to mediator agent z.
At the same time, the maximum values V
⊤
k
of the
non-base variables that are known by k are sent. k
also sends the request that x
j
B
is changed to a new
base. The request, d
m+1, j
B
, which has been received
from z, and row vector d
−
i
N
are sent to agents whose
constraints are affected by the variables contained in
the constraint of i
N
th row. When agent k
′
receives the
request of new base x
j
B
from agent k, k
′
updates D
k
′
and h
k
′
based on d
m+1, j
B
and d
−
i
N
, which are received
in the same message. Then k
′
sends d
m+1,k
′
to me-
diator z. The maximum values V
⊤
k
′
of the non-base
variables that are known by k
′
are also sent.
1 initialize D
z
. t
z
← 0. add t
z
to set T.
2 until the processing is terminated do {
3 while z’s receive queue is not empty
4 ∧ the loop is not broken do { receive a message.}
5 maintenance. }
6 receive (OV, d
m+1,k
, V
⊤
k
, X
↑
k
, set of X
↓
k, j
, x, p)
7 from agent k {
8 store/update d
m+1,k
, V
⊤
k
, X
↑
k
and set of X
↓
k, j
.
9 t
x
← t
x
+ p for t
x
in T. }
10 maintenance {
11 if t = 1 for all t in T then {
12 empty T. select new bases X
B
.
13 if X
B
is empty { terminate the processing. }
14 foreach x
j
B
in X
B
do {
15 select agent k that has minimum v
⊤
j
B
in V
⊤
k
.
16 t
j
B
← 0. add t
j
B
to set T.
17 send (BV, j
B
, d
m+1, j
B
, J
x
j
B
) to k. } } }
Figure 1: Processing in mediator z.
3.2 Area of Influence in Computation
The solution method needs to specify the agents that
are related to the exchange of bases. For that purpose,
agent k sends two sets X
↑
k
and X
↓
k, j
to mediator z. X
↑
k
ICAART 2012 - International Conference on Agents and Artificial Intelligence
230

1 initialize D
k
. initialize h
k
.
2 if h
k
∨ d
m+1,k
< 0 then { let d = 0.}
3 else { let d = d
m+1,k
. }
4 send (OV, d, V
⊤
k
, X
↑
k
, set of X
↓
k, j
, z, 1/n) to agent z.
5 until the processing is terminated do {
6 while k’s receive queue is not empty
7 ∧ the loop is not broken do { receive a message.} }
8 receive (BV, j
B
, d
m+1, j
B
, J
x
j
B
) from agent z {
9 select row i
N
10 corresponding to new non−base variable.
11 foreach j such that 1 ≤ j ≤ n do {
12 if h
j
∧ d
i
N
, j
= −1 then { h
j
← F. } }
13 save i
N
th row of D
k
as d
−
i
N
.
14 update i
N
th row of D
k
.
15 foreach i such that 1 ≤ i ≤ m,i 6= i
N
do {
16 update ith row of D
k
using i
N
th row of D
k
. }
17 update d
m+1,k
18 using i
N
th row of D
k
and d
m+1, j
B
of BV message.
19 h
j
B
← T.
20 if h
k
∨ d
m+1,k
< 0 then { let d = 0.}
21 else { let d = d
m+1,k
. }
22 send (OV, d, V
⊤
k
, X
↑
k
, set of X
↓
k, j
, j
B
, 1/|J
x
j
B
|)
23 to agent z.
24 foreach agent k
′
in J
x
j
B
\{k} do {
25 send (NBV, j
B
, d
m+1, j
B
of BV message, d
−
i
N
, |J
x
j
B
|)
26 to agent k
′
. } }
27 receive (NBV, j
B
, d
m+1, j
B , d
−
i
N
, |J
x
j
B
|) from agent k
′
{
28 foreach j such that 1 ≤ j ≤ n do {
29 if h
j
∧ jth element of d
−
i
N
= −1 then { h
j
← F. }
}
30 update d
−
i
N
similar to i
N
th row of D.
31 if k has i
N
th row then { update i
N
th row of D
k
. }
32 foreach i such that 1 ≤ i ≤ m,i 6= i
N
do {
33 update ith row of D
k
using i
N
th row of d
−
i
N
. }
34 update d
m+1,k
using d
−
i
N
and d
m+1, j
B
of BV message.
35 h
j
B
← T.
36 if h
k
∨ d
m+1,k
< 0 then { let d = 0.}
37 else { let d = d
m+1,k
. }
38 send (OV, d, V
⊤
k
, X
↑
k
, set of X
↓
k, j
, j
B
, 1/|J
x
j
B
|)
39 to agent z. }
Figure 2: Processing in non-mediator agent k.
is the set of the variables on which agent k depends.
X
↑
k
is computed by each agent k excluding mediator
z. As shown as follows, X
↑
k
is the set of variables that
are related to constraints contained in D
k
.
X
↑
k
= {x
j
| (d
i, j
∈ D
k
∧ 1 ≤ i ≤ m∧ 1 ≤ j ≤ n∧ (9)
d
i, j
6= 0) ∧ (h
j
∈ h
k
∧ 1 ≤ j ≤ n∧ h
j
)}
Here, the condition of h
j
is necessary to inform k that
base x
j
is changed to a non-base.
X
↓
k, j
is the set of variables, which is affected in the
case where agent k changes non-base x
j
to a newbase.
X
↓
k, j
is computed if at least one non-base variable x
j
relates to a constraint that is known by k and the max-
imum number v
⊤
j
of x
j
is bounded by a constraint.
Otherwise, the set is empty. Here let i
N
denote the
row of D
k
that corresponds to a new non-base in the
case of new base x
j
. As shown as follows, X
↓
k, j
is the
set of variables that are related to the constraint of i
N
th
row.
X
↓
k, j
=



{x
j
|d
i
N
, j
∈ D
k
,
1 ≤ j ≤ n,d
i
N
, j
6= 0}
¬h
k
∧
x
j
is bounded
φ otherwise
(10)
X
↓
k, j
can be computed before deciding whether vari-
able x
j
is selected as the new base or not.
When mediator agent z selects new base x
j
B
, the
set J
x
j
B
of the agents that relates to the change of basis
is shown as follows.
J
x
j
B
= { j|∃x ∈ X
↓
k, j
B
,x ∈ X
↑
j
} (11)
Here k represents the agent in which the maximum
value v
⊤
j
B
of x
j
B
is minimum.
3.3 Employing Parallelism
In earlier steps of the solution method for sparse prob-
lems, it is possible to update multiple bases that do not
interfere with each other in parallel. To employ the
parallelism, the selection of the new base in mediator
z is extended. In the extended processing, non-base
variables that have positive coefficients of the objec-
tive function are sorted in descending order. Then in-
dependent updates of bases are enumerated based on
the ordering. The first non-base is always selected as
a new base. The following non-bases are similarly se-
lected if they do not interfere with other new bases.
Set J
x
j
B
of agents that relates to the update of new
base x
j
B
is shown in Equation (11). Set X
B
of the new
bases is shown as follows.
∀x
j
B
∈ X
B
,∀x
j
B
′
∈ X
B
, j
B
6= j
B
′
,J
x
j
B
∩J
x
j
B
′
= φ (12)
3.4 Pseudo Code
Pseudo codes of the solution method are shown in
Figures 1 and 2. In this processing, three types of
messages are employed as follows. OV message
transports coefficient values of the objective function
and related information from each agent to mediator
z. BV message transports requests of changing new
bases from mediator to related agents. NBV mes-
sage propagates requests of changing new bases from
ANALYSIS FOR DISTRIBUTED COOPERATION BASED ON LINEAR PROGRAMMING METHOD
231

Table 1: Results.
(a) #cycles until termination (b) #parallel upd. (c) #terms in const. (d) #agents related to upd.
alg. ser par
a o n m min. max. ave. min. max. ave. min. max. ave. min. max. ave. min. max. ave.
2 1 20 10 20 35 30 11 32 25 1 2 1.27 4 12 5.00 7 20 11.02
40 20 47 65 57 23 41 30 1 5 2.07 4 22 5.26 7 40 12.08
80 40 92 122 110 20 41 30 1 9 3.97 4 23 5.20 7 57 11.40
3 2 20 10 20 38 28 20 38 28 1 1 1 5 12 7.09 12 20 16.85
40 20 41 62 52 32 59 42 1 2 1.26 5 22 7.75 12 40 21.95
80 40 86 116 103 38 80 53 1 5 2.08 5 37 8.38 12 80 23.47
4 3 20 10 17 38 26 17 38 26 1 1 1 6 12 8.69 17 20 19.41
40 20 32 74 53 29 71 54 1 2 1.05 6 22 11.15 17 40 31.09
80 40 86 113 98 53 101 72 1 3 1.44 6 42 12.44 17 80 41.06
the agents that have received the requests to related
agents.
Figure 1 shows the processing in mediator agent
z. After the initialization, z waits for OV messages
from other agents. z detects that all OV messages are
received using set T of the counter for the termination
detection. Then z selects set X
B
of new bases that can
be updated in parallel. The changing of new bases is
requested by sending BV messages. When set X
B
of
new bases is empty, mediator z detects the termina-
tion of the solution methods. In the case where X
B
is not empty and no agent can update the bases, me-
diator z also detects the situation that the problem is
unbounded.
Figure 2 shows the processing in non-mediator
agent k. After the initialization, k waits for BV mes-
sages from mediator z or NBV messages from other
agents k
′
. When either message is received, k updates
D
k
and h
k
. Then consequent messages are sent. When
the solution method is terminated, there are the cases
where the constraint of each base variable x
k
does not
exist in agent k. In that case, to determine k’s assign-
ment, the agent that has the constraint has to notify k
of the constraint in post processing.
4 EXPERIMENTS
4.1 Settings of Experiments
We evaluated the example problems whose con-
straints partially overlap with neighborhood variables
on a ring network. The problem is considered as the
situation where neighboring agents share a limited
amount of resources. Parameters to generate the prob-
lem are as follows. n
D
: the number of the decision
variables. n
D
excludes the number of additional slack
variables that is the same as the number of the con-
straints. a: the number of decision variables for each
constraint. o: the number of overlapping variables in
a constraint that overlaps with the next constraint in
the ring network. [v
O⊥
,v
O⊤
): the range of the coeffi-
cients of the objective function. [v
C⊥
,v
C⊤
): the range
of the coefficients of the constraints. [v
R⊥
,v
R⊤
): the
range of the parameter for the constants of the con-
straints. For each constraint, the parameter represents
the ratio of the constant to the summation of all coef-
ficients.
Here, n
D
Ca and o are set so that the constraints
are uniformly placed on the ring network. The val-
ues of coefficients and constants are randomly deter-
mined with uniform distribution. In the following,
the problems are represented using the total number
n = n
D
+ m of variables, the number m of constraints,
a and o. [v
O⊥
,v
O⊤
) and [v
C⊥
,v
C⊤
) are respectively
[1,3). [v
R⊥
,v
R⊤
) is [0.5,1). The results are totaled for
20 instances.
The following two methodsare compared. ser: the
baseline method that sequentially updates bases. par:
the method that employ parallelism if possible. When
there is no parallelism, both methods work similarly.
As the criteria of the execution time, we used the
number of the cycles of exchanging messages. In a
cycle, the following processing is performed. First,
each agent processes all messages in its own receiv-
ing queue and puts messages in the sending queue if
necessary. Then the simulator moves the messages
from the sending queues to the destinations’ receiv-
ing queues for all agents.
4.2 Results
The number of cycles until the termination is shown
in Table 1(a). Generally, the method par that simul-
taneously updates multiple new bases terminates in
a lower number of cycles. In very sparse problems
like (a,o, n, m) = (2, 1,80,40), par effectively reduces
the number of cycles. On the other hand, in prob-
lems like (n,m) = (20, 10) and (a, o) = (4, 3) whose
constraints are relatively overlapped, the effects are
small. The number of parallel updates of new bases
is shown in Table 1(b). The problems in which the
ICAART 2012 - International Conference on Agents and Artificial Intelligence
232

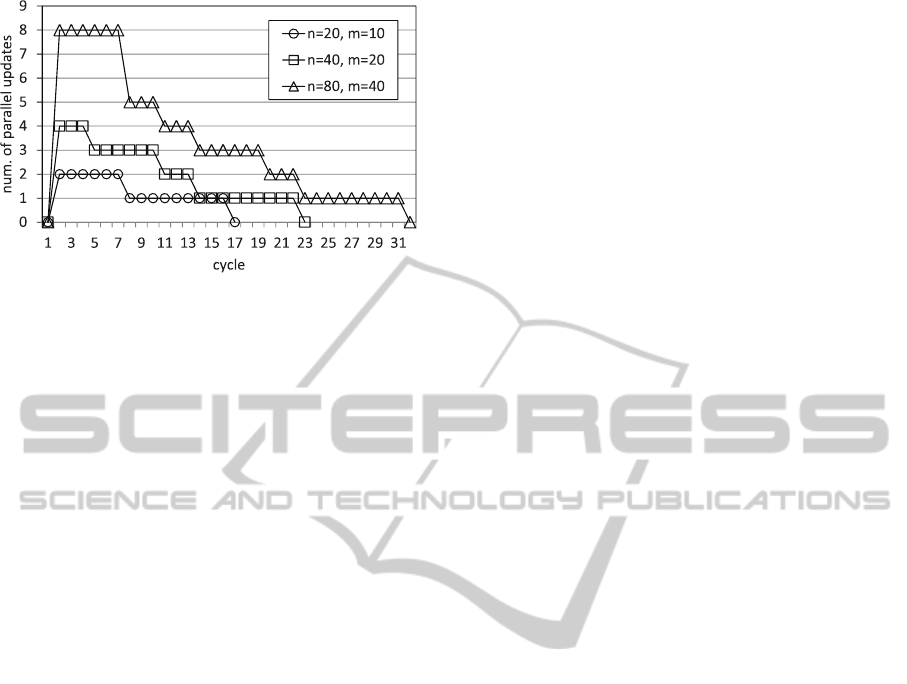
Figure 3: Transition of number of parallel updates of new
basis (par, a = 2, o = 1).
number of cycles is effectively reduced as shown in
Table 1(a) have a relatively large number in the paral-
lelism. The number of terms in a constraint is shown
in Table 1(c). The result represents that the size of
the constraints increases with the progress of the so-
lution method. Although the maximum number of the
terms is less than the number of the variables, the par-
allelism is lost as shown above. Table 1(d) shows the
number of agents related to an update of a new base.
The maximum number that equals the number of vari-
ables represents that the locality of updates was lost in
later cycles.
The transition of the number of parallel updates
of the new basis for an example problem a = 2,o = 1
is shown in Figure 3. The number of parallelism is
relatively large in the first steps and decreases in later
cycles. There are two reasons of the decrement. One
reason is that the possible new bases are eliminated
by the solution method. Another is that the number of
variables in the updated constraints increases.
5 CONCLUSIONS
In this work, we studied a framework of distributed
cooperative problem solving based on the linear pro-
gramming method. Essential processing for dis-
tributed cooperation and extracting the parallelism
are shown. While there is possibility of parallel up-
dates of the new bases in the sparse problems, the
global tantalization of the information is necessary
for the selection of new bases, and the extraction of
the parallelism. Instead of the mediator, there are
opportunities to decompose the tantalization using a
tree structure of agents. Considering the fact that
the locality of the problem is lost with the progress
of the solution method, there is the possibility of an
approach in which agents store the revealed infor-
mation and employ it to reduce distributed process-
ing. In (Burger et al., 2011), each step of the sim-
plex method is not decomposed. Instead, each agent
solves local problems and exchanges the sets of cur-
rent bases. Although we focused on the sparse prob-
lems and the more distributed solver, the possibility
of using the characteristics should be investigated to
divide columns and to avoid synchronization. De-
composition of the processing of the mediator using
a structured group of agents, applying efficient meth-
ods, and comparison/integration with related works
will be included in future works.
ACKNOWLEDGEMENTS
This work was supported in part by a Grant-in-Aid for
Young Scientists (B), 22700144.
REFERENCES
Burger, M., Notarstefano, G., Allgower, F., and Bullo, F.
(2011). A distributed simplex algorithm and the multi-
agent assignment problem. In American Control Con-
ference, pages 2639–2644.
Chvatal, V. (1983). Linear programming. W.H.Freeman
Company.
Ho, J. K. and Sundarraj, R. P. (1994). On the efficacy
of distributed simplex algorithms for linear program-
ming. Computational Optimization and Applications,
3:349–363.
Mailler, R. and Lesser, V. (2004). Solving distributed con-
straint optimization problems using cooperative me-
diation. In 3rd International Joint Conference on Au-
tonomous Agents and Multiagent Systems, pages 438–
445.
Modi, P. J., Shen, W., Tambe, M., and Yokoo, M. (2005).
Adopt: Asynchronous distributed constraint optimiza-
tion with quality guarantees. Artificial Intelligence,
161(1-2):149–180.
Petcu, A. and Faltings, B. (2005). A scalable method
for multiagent constraint optimization. In 9th Inter-
national Joint Conference on Artificial Intelligence,
pages 266–271.
Wei, E., Ozdaglar, A., and Jadbabaie, A. (2010). A dis-
tributed newton method for network utility maximiza-
tion. In 49th IEEE Conference on Decision and Con-
trol, CDC 2010, pages 1816 –1821.
Yarmish, G. and Van Slyke, R. (2009). A distributed,
scaleable simplex method. The Journal of Supercom-
puting, 49:373–381.
ANALYSIS FOR DISTRIBUTED COOPERATION BASED ON LINEAR PROGRAMMING METHOD
233