
MERGING SUCCESSIVE POSSIBILITY DISTRIBUTIONS FOR
TRUST ESTIMATION UNDER UNCERTAINTY IN MULTI-AGENT
SYSTEMS
Sina Honari
1
, Brigitte Jaumard
1
and Jamal Bentahar
2
1
Department of Computer Science and Software Engineering, Concordia University, Montreal, Canada
2
Concordia Institute for Information System Engineering, Concordia University, Montreal, Canada
K
eywords:
Possibility theory, Multi-agent systems, Uncertainty in AI.
Abstract:
In social networks, estimation of the degree of trustworthiness of a target agent through the information ac-
quired from a group of advisor agents, who had direct interactions with the target agent, is challenging. The
estimation gets more difficult when, in addition, there is some uncertainty in both advisor and target agents’
trust. The uncertainty is tackled when (1) the advisor agents are self-interested and provide misleading ac-
counts of their past experiences with the target agents and (2) the outcome of each interaction between agents
is multi-valued. In this paper, we propose a model for such an evaluation where possibility theory is used to
address the uncertainty of an agent’s trust. The trust model of a target agent is then obtained by iteratively
merging the possibility distributions of: (1) the trust of the estimator agent in its advisors, and (2) the trust of
the advisor agents in a target agent. Extensive experiments validate the proposed model.
1 INTRODUCTION
Social networking sites have become the preferred
venue for social interactions. Despite the fact that
social networks are ubiquitous on the Internet, only
few websites exploit the potential of combining user
communities and online marketplaces. The reason
is that users do not know which other users to trust,
which makes them suspicious of engaging in online
business, in particular if many unknown other parties
are involved. This situation, however, can be allevi-
ated by developing trust metrics such that a user can
assess and identify trustworthy users. In the present
study, we focus on developing a trust metric for es-
timating the trust of a target agent, who is unknown,
through the information acquired from a group of ad-
visor agents who had direct experience with the target
agent, subject to possible trust uncertainty.
Each entity in a social network can be represented
as an agent who is interacting with its network of
trustees, which we refer to as advisors, where each
advisor agent in turn is in interaction with an agent of
interest, which we refer to as a target agent. Each
interaction can be considered as a trust evaluation
between the trustor agent, i.e., the agent who trusts
another entity, and the trustee agent, i.e., the agent
whom is being trusted. In the context of interactions
between a service provider (trustee) and customers
(trustors), some companies (e.g., e-bay and amazon)
provide means for their customers to provide their
feedback on the quality of the services they receive,
under the form of a rating chosen out of a finite set
of discrete values. This leads to a multi-valued do-
main of trust, where each trust rating represents the
level of trustworthiness of the trustor agent as viewed
by the trustee agent. While most of the web applica-
tions ask users to provide their feedbacks within such
a multi-valued rating domain, most studies (Jøsang,
2001), (Wang and Singh, 2010), (Reece et al., 2007)
and (Teacy et al., 2006) are restricted to binary do-
mains. Hence, our motivation for developing a multi-
valued trust domain where each agent can be evalu-
ated within a multi-valued set of ratings.
An agent may ask its advisors to provide infor-
mation on a target agent who is unknown to him.
The advisors are not necessarily truthful (e.g., com-
petition among market shares, medical records when
buying a life insurance) and therefore may manipu-
late their information before reporting it. In addition,
the advisor agents’ trustworthy behavior may differ
from one interaction to another, leading to some un-
certainty about the advisors’ trustworthiness and the
180
Honari S., Jaumard B. and Bentahar J..
MERGING SUCCESSIVE POSSIBILITY DISTRIBUTIONS FOR TRUST ESTIMATION UNDER UNCERTAINTY IN MULTI-AGENT SYSTEMS.
DOI: 10.5220/0003754301800189
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 180-189
ISBN: 978-989-8425-95-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

accuracy of information revealed by them.
Possibility distribution is a flexible tool for mod-
eling an agent’s trust considering such uncertainties
where the agent’s trust arises from an unknown prob-
ability distribution. Possibility theory was first in-
troduced by (Zadeh, 1978) and further developed by
Dubois and Prade (Dubois and Prade, 1988). It has
been utilized, e.g., to model reliability (Delmotte and
Borne, 1998). We use possibility distributions to rep-
resent the trust of an agent in order to consider the
uncertainties in the agent’s trustworthiness. Later, we
propose merging of the possibility distributions of an
agent’s trust in it’s advisors with the reported possi-
bility distributions by the advisors on a target agent’s
trust. The resulted possibility distribution is an esti-
mation of the target agent’s trust. Finally, we intro-
duce 2 evaluation metrics and provide extensive ex-
periments to validate our proposed tools.
The rest of the paper is structured as follows: Sec-
tion 2 describes the related works. In Section 3, we
provide a detailed description of our problem environ-
ment. Section 4 discusses some fusion rules for merg-
ing possibility distributions considering the agents’
trust. In Section 6, we propose our merging approach
of the possibility distributions in order to estimate the
target agent’s trust. Extensive experimental evalua-
tions are presented in Section 7 to validate the pro-
posed trust model.
2 RELATED WORK
Considerable research has been accomplished in
multi-agent systems providing models of trust and
reputation, a detailed overview of which is provided
in (Ramchurn et al., 2004). In reputation models, an
aggregation of opinions of members towards an indi-
vidual member which is usually shared among those
members is maintained. Starting with (Zacharia et al.,
2000), the reputation of an agent can be evaluated and
updated by agents over time. However, it is implic-
itly assumed that the agent’s trust is a fixed unknown
value at each time slot which does not capture the un-
certainties in an agent’s trust. Regret (Sabater and
Sierra, 2001) is another reputation model which de-
scribes different dimensions of reputation (e.g. “indi-
vidual dimension”, “social dimension”). However, in
this model the manipulation of information and how
it can be handled is not addressed.
Some trust models try to capture different dimen-
sions of trust. In (Griffiths, 2005) a multi-dimensional
trust containing elements like success, cost, timelines
and quality is presented. The focus in this work is
on the possible criteria that is required to build a trust
model. However, the uncertainty in an agent’s behav-
ior and how it can be captured is not considered.
The work of (Huynh et al., 2006) estimates the
trust of an agent considering “direct experience”,
“witness information”, “role-based rules” and “third-
party references provided by the target agents”. Al-
though the latter 2 aspects are not included in our
model, it is based on the assumption that the agents
are honest in exchanging information with one an-
other. In addition, despite the fact that the underlying
trust of an agent is assumed to have a normal distribu-
tion, the estimated trust is a single value instead of a
distribution. In other words, it does not try to measure
the uncertainty associated with the occurrence of each
outcome of the domain considering the results of the
empirical experiments.
In all of the above works the uncertainty in the
trust of an agent is not considered. We now re-
view the works that address uncertainty. Reece et al.
(Reece et al., 2007) present a multi-dimensional trust
in which each dimension is binary (successful or un-
successful) and corresponds to a service provided in a
contract (video, audio, data service, etc.). This paper
is mainly concentrated on fusing information received
from agents who had direct observations over a sub-
set of services (incomplete information) to derive the
complete information on the target entity while our
work focuses on having an accurate estimation when
there is manipulation in the acquired information.
Yu and Singh (Yu and Singh, 2002) measure the
probability of trust, distrust and uncertainty of an
agent based on the outcome of interactions. The un-
certainty measured in this work is equal to the fre-
quency of the interaction results in which the agent’s
performance is neither highly trustworthy nor highly
untrustworthy which can be inferred as lack of both
trust and distrust in the agent. However, the uncer-
tainty that we capture is the change in the agent’s de-
gree of trustworthiness regardless of how trustworthy
the agent is. In other words, when an agent acts with
high uncertainty it’s degree of trustworthiness is hard
to predict for future interactions. We do not consider
uncertainty as lack of trust or distrust, but the variabil-
ity in the degree of trustworthiness. In both works of
(Yu and Singh, 2002) and (Reece et al., 2007) the pos-
sibility of having malicious agents providing falsified
reports is ignored.
The works of (Jøsang, 2001) and (Wang and
Singh, 2010) provide probabilistic computational
models measuring belief, disbelief and uncertainty
from binary interactions (positive or negative). Al-
though the manipulation of information by the re-
porter agents is not considered in these works, they
split the interval of [0,1] between these 3 elements
MERGING SUCCESSIVE POSSIBILITY DISTRIBUTIONS FOR TRUST ESTIMATION UNDER UNCERTAINTY IN
MULTI-AGENT SYSTEMS
181

measuring a single value for each one of them. We do
not capture uncertainty in the same sense by measur-
ing a single value, instead we consider uncertainty by
measuring the likelihood of occurrence of every trust
element in the domain and therefore catch the possi-
ble deviation in the degree of trustworthiness of the
agents.
One of the closest works to our model which in-
cludes both uncertainty and the manipulation of infor-
mation is Travos (Teacy et al., 2006). Although this
work has a strong probabilistic approach and covers
many issues, it is yet restricted to binary domain of
events where each interaction, which is driven from
the underlying probability that an agent fulfills it’s
obligations, is either successful or unsuccessful. Our
work is a generalization of this work in the sense that
it is extended to a multi-valued domain where we as-
sociate a probability to the occurrence of each trust
value in the domain. Extension of the Travos model
from binary to multi-valued event in the probabilis-
tic approach is quite challenging due to its technical
complexity. We use possibility theory which is a flex-
ible and strong tool to address uncertainty and at the
same time it is applicable to multi-valued domains.
3 MULTI-AGENT PLATFORM
In this section, we present the components that build
the multi-agent environment and the motivation be-
hind each choice. We first discuss the set of trust
values (Section 3.1), the agent’s internal trust distri-
bution (Section 3.2) and the interactions among the
agents (Section 3.3). Later, we describe the forma-
tion of the possibility distribution of an agent’s trust
(Section 3.4) and the possible agent information ma-
nipulations (Section 3.5). Finally, the game scenario
in this paper is discussed (Section 3.6).
3.1 Trust Values
Service providers ask customers to provide their feed-
backs on the received services commonly in form of a
rating selected from a multi-valued set. The selected
rating indicates a customer’s degree of satisfaction or,
in other words, its degree of trust in the provider’s
service. This motivates us to consider a multi-valued
trust domain. We define a discrete multi-valued set
of trust ratings denoted by T, with τ being the low-
est, τ being the highest and |T| representing the num-
ber of trust ratings. All trust ratings are within [0,1]
and they can take any value in this range. However,
if the trust ratings are distributed in equal intervals,
the ith trust rating equals to: (i − 1)/(|T| − 1) for
i = 1,2,...,|T|. For example, if |T| = 5, then the set
of trust ratings is {0,0.25,0.5,0.75, 1}.
3.2 Internal Probability Distribution of
an Agent’s Trust
In our multi-agent platform, each agent is associ-
ated with an internal probability distribution of trust,
which is only known to the agent. This allows mod-
eling a specific degree of trustworthiness in that agent
where each trust rating τ is given a probability of oc-
currence. In order to model a distribution, given its
minimum, maximum, peak, degree of skewness and
peakness, we use a form of beta distribution called
modified pert distribution (Vose, 2008). It can be
replaced by any distribution that provides the above
mentioned parameters. Well known distributions,
e.g., normal distribution, are not employed as they do
not allow positive or negative skewness of the distri-
bution. In modified pert distribution, the peak of the
distribution, which is denoted by τ
PEAK
a
, has the high-
est probability of occurrence. This means that while
the predominant behavior of the agent is driven by
τ
PEAK
a
and the trust ratings next to it, there is a small
probability that the agent does not follow its domi-
nant behavior. Figure 1(a) demonstrates an example
of the internal trust distribution of an agent. The more
the peak of the internal distribution is closer to τ, the
more trustworthy the agent is and vice-versa.
3.3 Interaction between Agents
When a customer rates a provider’s service, its rating
depends not only on the provider’s quality of service
but also on the customer’s personal point of view. In
this paper, we just model the provider’s quality of ser-
vice. In each interaction a trustor agent, say α, re-
quests a service from a trustee agent, say β. Agent
β should provide a service in correspondence with its
degree of trustworthiness which is implied in its inter-
nal trust distribution. On this purpose, it generates a
random value from the domain of T by using its inter-
nal probability distribution of trust. The peak of the
internal trust distribution, τ
PEAK
a
, has the highest prob-
ability of selection while other trust ratings in T have
a relatively smaller probability to be chosen. This will
produce a mostly specific and yet not deterministic
value. Agent β reports the generated value to α which
represents the quality of service of β in that interac-
tion.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
182

(a) Internal Prob. Dist. of a (b) Network of Agents
Figure 1: Multi-Agent Platform.
3.4 Building Possibility Distribution of
Trust
Upon completion of a number of interactions between
a trustor agent, α, and a trustee agent, β, agent α can
model the internal trust distribution of β, by usage of
the values received from β during their interactions.
If the number of interactions between the agents is
high enough, the frequencies of each trust rating can
almost represent the internal trust distribution of β.
Otherwise, if few interactions are made, the randomly
generated values may not represent the underlying
distribution of β’s trust (Masson and Denœux, 2006).
In order to model an agent α’s trust with respect to
the uncertainty associated with the occurrence of each
trust rating in the domain, we use possibility distribu-
tions which can present the degree of possibility of
each trust rating in T. A possibility distribution is de-
fined as: Π : T → [0,1] with max
τ∈T
Π(τ) = 1.
We apply the approach of (Masson and Denœux,
2006) to build a possibility distribution from empir-
ical data given the desired confidence level. In this
approach, first simultaneous confidence intervals for
all trust ratings in the domain are measured by usage
of the empirical data (which in our model are derived
from interaction among agents). Then, the possibil-
ity of each trust rating τ considering the confidence
intervals of all trust ratings in T is found.
3.5 Manipulation of the Possibility
Distributions
An agent, say a
S
, needs to acquire information about
the degree of trustworthiness of agent a
D
unknown to
him. On this purpose, it acquires information from its
advisors like a who are known to a
S
and have already
interacted with a
D
. Agent a is not necessarily truthful
for reasons of self-interest, therefore it may manipu-
late the possibility distribution it has built about a
D
’s
trust before reporting it to a
S
. The degree of manip-
ulation of the information by agent a is based on its
internal probability distribution of trust. More specif-
ically, if the internal trust distribution of agents a and
a
′
indicate that a’s degree of trustworthiness is lower
than a
′
, then the reported possibility distribution of a
is more prone to error than a
′
. The following 2 algo-
rithm introduced in this section are examples of ma-
nipulation algorithms:
Algorithm I
for each τ ∈ T do
τ
′
← random trust rating from T, according
to agent a’s internal trust distribution
error
τ
= 1− τ
′
Π
a→a
D
(τ) =
b
Π
a→a
D
(τ) + error
τ
end for
where
b
Π
a→a
D
(τ) is the possibility distribution built
by a through its interactions with a
D
and Π
a→a
D
(τ)
is the manipulated possibility distributions. In this
algorithm for each trust rating τ ∈ T a random trust
value, τ
′
, is generated following the internal trust dis-
tribution of agent a. For highly trustworthy agents,
the randomly generated value of τ
′
is closer to τ and
the subsequent error (error
τ
) is closer to 0. Therefore
the manipulation of
b
Π
a→a
D
(τ), is insignificant. On
the other hand, for highly untrustworthy agents, the
value of τ
′
is closer to τ and therefore the derived er-
ror, error
τ
, is closer to 1. In such a case, the possibility
value of
b
Π
a→a
D
(τ) is considerably modified causing
noticeable change in the original values.
After measuring the distribution of Π
a→a
D
(τ), it is
normalized and then reported to a
S
. The normaliza-
tion satisfies: (1) the possibility value of every trust
rating τ in T is in [0,1], and (2) the possibility value of
at least one trust rating in T equals to 1. let
e
Π(τ) be a
non-normalized possibility distribution. Either of the
following formulas (Delmotte and Borne, 1998) gen-
erates a normalized possibility distribution of Π(τ):
(1) Π(τ) =
e
Π(τ)/h, (2) Π(τ) =
e
Π(τ) + 1− h,
where h = max
τ∈T
e
Π(τ).
Here is the second manipulation algorithm:
Algorithm II:
for each τ ∈ T do
τ
′
← random trust rating from T, according
to agent a’s internal trust distribution
max error
τ
= 1− τ
′
error
τ
= random value in [0,max error
τ
]
Π
a→a
D
(τ) =
b
Π
a→a
D
(τ) + error
τ
end for
As for algorithm I, the distribution of Π
a→a
D
(τ)
is normalized before being reported to a
S
. In al-
gorithm II, an additional random selection value is
added where the random value is selected uniformly
in [0,max error
τ
]. In algorithm I, the trust rating of
τ
PEAK
a
and the trust values next to it have a high proba-
bility of being selected. The error added to
b
Π
a→a
D
(τ)
MERGING SUCCESSIVE POSSIBILITY DISTRIBUTIONS FOR TRUST ESTIMATION UNDER UNCERTAINTY IN
MULTI-AGENT SYSTEMS
183

may be neglected when the distribution is normal-
ized. However, in algorithm II, if an agent is highly
untrustworthy the random trust value of τ
′
is close
to τ and thereupon the error value of max error
τ
is
close to 1. This causes the uniformly generated value
in [0,max error
τ
] considerably random and unpre-
dictable which makes the derived possibility distri-
bution highly erroneous after normalization. On the
other hand, if an agent is highly trustworthy, the error
value of max error
τ
is close to τ and the random value
generated in [0,max error
τ
] would be even smaller,
making the error of the final possibility distribution
insignificant. While incorporating some random pro-
cess, both algorithms manipulate the possibility dis-
tribution based on the agent’s degree of trustworthi-
ness causing the scale of manipulation by more trust-
worthy agents smaller and vice-versa. However, the
second algorithm acts more randomly. We provide
these algorithms to observe the extent of dependency
of the derived results in respect to a specific manipu-
lation algorithm employed.
3.6 Game Scenario
In this paper, we study a model arising in social net-
works where agent a
S
makes a number of interac-
tions with each agent a in a set A = {a
1
,a
2
,...,a
n
} of
n agents (agent a
S
’s advisors), assuming each agent
a ∈ A has carried out some interactions with agent a
D
.
Agent a
S
builds a possibility distribution of trust for
each agent in A by usage of the empirical data de-
rived throughout their interactions. Each agent in A,
in turn, builds an independent possibility distribution
of trust through its own interactions with agent a
D
.
When a
S
wants to evaluate the level of trustworthi-
ness of a
D
, who is unknown to him, it acquires in-
formation from its advisors, A, to report their mea-
sured possibility distributions on a
D
’s trust. Agents in
A are not necessarily truthful. Therefore, through us-
age of the manipulation algorithms, they manipulate
their own possibility distributions of
b
Π
a→a
D
(τ) in cor-
respondence with their degree of trustworthiness and
report the manipulated distributions to a
S
. Agent a
S
uses the reported distributions of Π
a→a
D
(τ) by each
agent a ∈ A and its trust distribution in agent a, rep-
resented by Π
a
S
→a
(τ), in order to estimates the possi-
bility distribution of a
D
’s trust.
4 FUSION RULES CONSIDERING
THE TRUST OF THE AGENTS
Let τ
a
S
→a
∈ [0, 1] be a single trust value of agent a
S
in agent a and Π
a→a
D
(τ),τ ∈ T represent the possi-
bility distribution of agent a’s trust in agent a
D
as
reported by a to a
S
. We now look at different fu-
sion rules for merging the possibility distributions of
Π
a→a
D
(τ),a ∈ A, with respect to the trust values of
τ
a
S
→a
,∀a ∈ A, in order to get a possibility distribution
of Π
a
S
→a
D
(τ),τ ∈ T, representing a
S
’s trust in a
D
. We
explore three fusion rules, which are the most com-
monly used. The first one is the Trade-off (To) rule
(Yager, 1996), which builds a weighted mean of the
possibility distributions:
Π
To
a
S
→a
D
(τ) =
∑
a∈A
ω
a
× Π
a→a
D
(τ), (1)
where ω
a
= τ
a
S
→a
/
∑
a∈A
τ
a
S
→a
for τ ∈ T, and
Π
To
a
S
→a
D
(τ) indicates the trust of a
S
in a
D
measured
by Trade-off rule. Note that the trade-off rule con-
siders all of the possibility distributions reported by
the agents in A. However, the degree of influence of
the possibility distribution of Π
a→a
D
(τ) is weighted
by the normalized trust of agent a
S
in each agent a
(which is ω
a
).
The next two fusion rules belong to a family
of rules which modify the possibility distribution of
Π
a→a
D
(τ) based on the trust value associated with it,
τ
a
S
→a
, and then take an intersection (Zadeh, 1965) of
the modified distributions. We refer to this group of
fusion rules as Trust Modified (TM) rules. Therein,
if τ
a
S
→a
= 1, Π
a→a
D
(τ) remains unchanged, meaning
that agent a
S
’s full trust in a results in total acceptance
of possibility distribution of Π
a→a
D
(τ) reported by a.
The less agent a is trustworthy the less its reported
distribution is reliable and consequently its reported
distribution of Π
a→a
D
(τ) is moved closer towards a
uniform distribution by TM rules. In the context of
possibility distributions, the uniform distribution pro-
vides no information as all trust values in domain T
are equally possible which is referred to as complete
ignorance (Dubois and Prade, 1991). Indeed, nothing
differentiates between the case where all elements in
the domain have equal probability and the case where
no information is available (complete ignorance). The
more a distribution of Π
a→a
D
(τ) gets closer to a uni-
form distribution, the less likely is would get to be
selected in the intersection phase (Zadeh, 1965). We
selected the following 2 TM fusion rules:
Yager (Yager, 1987):
Π
Y
a
S
→a
D
(τ) = min
a∈A
[τ
a
S
→a
× Π
a→a
D
(τ) + 1− τ
a
S
→a
].
Dubois and Prade (Dubois and Prade, 1992):
Π
DP
a
S
→a
D
(τ) = min
a∈A
[max(Π
a→a
D
(τ),1− τ
a
S
→a
)].
In Yager’s fusion rule, the possibility of each trust
value τ moves towards a uniform distribution as much
ICAART 2012 - International Conference on Agents and Artificial Intelligence
184

as (1−τ
a
S
→a
) which is the extent to which the agent a
is not trusted. In Dubois and Prade’s fusion rule, when
an agent’s trust declines, the max operator would
more likely select 1 − τ
a
S
→a
and, hence, the informa-
tion in Π
a→a
D
(τ) reported by a gets closer to a uni-
form distribution.
Once a fusion rule in this Section is applied, the
resulted possibility distribution of Π
a
S
→a
D
(τ),τ ∈ T
is then normalized to represent the possibility distri-
bution of agent a
S
’s trust in a
D
.
5 MERGING SUCCESSIVE
POSSIBILITY DISTRIBUTIONS
In this section, we present the main contribution, i.e.,
a methodologyfor merging the possibility distribution
of Π
a
S
→a
(τ) (representing the trust of agent a
S
in its
advisors) with the possibility distribution of Π
a→a
D
(τ)
(representing the trust of the agent set A in agent a
D
).
These 2 possibility distributions are associated to the
trust of entities at successive levels in a multi-agents
systems and hence giving it such a name.
In order to perform such a merging, we need to
know how the distribution of Π
a→a
D
(τ) changes, de-
pending on the characteristics of the possibility dis-
tribution of Π
a
S
→a
(τ). We distinguish the following
cases for a proper merging of the successive possibil-
ity distributions.
Specific Case. Consider a scenario where ∃!τ
′
,τ ≤
τ
′
≤ τ and Π
a
S
→a
(τ) =
(
1, τ = τ
′
0, otherwise
, i.e., only
one trust value is possible in the domain of T and
the possibility of all other trust values is equal to 0.
Then, trust of agent a
S
in agent a can be associated
with a single value of τ
a
S
→a
= τ
′
and the fusion rules
described in section 4 can be applied to get the pos-
sibility distribution of Π
a
S
→a
D
(τ).
Considering the TM fusion rules, for each agent a,
first the possibility distribution of Π
a→a
D
(τ) is trans-
formed based on the trust value of τ
a
S
→a
= τ
′
as dis-
cussed in Section 4. Then, an intersection of the
transformed possibility distribution is taken and the
resulted distribution is normalized to get the possibil-
ity distribution of Π
a
S
→a
D
(τ).
General Case. For each agent a, we have a subset of
trust ratings, which we refer to as T
POS
a
, such that:
1) T
POS
a
⊂ T,
2) If Π
a
S
→a
(τ) > 0, then τ ∈ T
POS
a
,
3) If Π
a
S
→a
(τ) = 0, then τ ∈ {T − T
POS
a
}.
Each trust rating value in T
POS
a
is possible. This
means that the trust of agent a
S
in a can possibly take
any value in T
POS
a
and consequently any trust rating
τ ∈ T
POS
a
can be possibly associated with τ
a
S
→a
. How-
ever, the higher the value of Π
a
S
→a
(τ), the higher the
likelihood of occurrence of trust rating τ ∈ T
POS
a
. We
use the possibility distribution of Π
a
S
→a
(τ) to get the
relative chance of happening of each trust rating in
T
POS
a
. In this approach, we give each trust rating τ, a
Possibility Weight (PW) equal to:
PW(τ) = Π
a
S
→a
(τ)/
∑
τ
′
∈T
POS
a
Π
a
S
→a(τ
′
)
.
Higher value of PW(τ) implies more occurrences
chance of the τ value. Hence, any trust rating τ ∈ T
POS
a
is possible to be observed with a weight of PW(τ) and
merged with Π
a→a
D
(τ) using one of the fusion rules.
Considering the General Case, there are a total
of |A| = n agents and each agent a has a total of
|T
POS
a
| possible trust values. For a possible esti-
mation of Π
a
S
→a
D
(τ), we need to choose one trust
rating of τ ∈ T
POS
a
for each agent a ∈ A. Having
|A| = n agents and a total of |T
POS
a
| possible trust
ratings for each agent a ∈ A, we can generate a to-
tal of
∏
a∈A
|T
POS
a
| = K possible ways of getting the
final possibility of Π
a
S
→a
D
(τ). This means that any
distribution out of K distributions is possible. How-
ever, they are not equally likely to happen. If agent a
S
chooses trust rating τ
1
for agent a
1
, τ
2
for agent a
2
,
and τ
n
for agent a
n
, then the possibility distribution
of Π
a
S
→a
D
(τ) derived from these trust ratings has an
Occurrence Probability(OP) of
n
∏
i=1
PW(τ
i
).
For every agent a, we have:
∑
τ∈T
POS
a
PW(τ) = 1,
then considering all agents we have:
∑
τ
1
∈T
POS
a
...
∑
τ∈∈T
POS
a
1
...
∑
τ
n
∈T
POS
a
n
PW(τ
1
)
× ... × PW(τ) × ... × PW(τ
n
) = 1. (2)
As can be observed in (2), the PW is normalized
in such a way that, by multiplying the PW (associated
with the trust rating of τ chosen in T
POS
a
for agent a)
of all the agents in A, the OP of the set of trust rat-
ings chosen for the agents in A, that derive a specific
Π
a
S
→a
D
(τ), can be estimated.
Trust Event Coefficient. The PW(τ) value shows the
relative possibility of τ compared to other values in
T of an agent a. However, we still need to compare
the possibility of a given trust rating τ, for an agent
a, compared to other agents in A. If the possibility
weights of two agents are equal, say 0.2 and 0.8 for
trust ratings τ and τ, and the number of interactions
MERGING SUCCESSIVE POSSIBILITY DISTRIBUTIONS FOR TRUST ESTIMATION UNDER UNCERTAINTY IN
MULTI-AGENT SYSTEMS
185

with the first agent is much higher than the second
agent, we need to give more credit to the first agent’s
reported distribution of Π
a→a
D
(τ)
. However, the cur-
rent model is unable of doing so. Therefore, we pro-
pose to use a Trust Event Coefficient for each trust
value τ, denoted by TEC(τ), in order to consider the
number of interactions, which satisfies:
1) If m
τ
= 0, TEC(τ) = 0
2) If Π
a
S
→a
(τ) = 0, TEC(τ) = 0
3) If m
τ
≥ m
τ
′
, TEC(τ) ≥ TEC(τ
′
)
4) If m
τ
= m
τ
′
and Π
a
S
→a
(τ) ≥ Π
a
S
→a
(τ
′
),
TEC(τ) ≥ TEC(τ
′
),
where τ ∈ T
POS
a
, m
τ
is the number of the occurrences
of trust rating τ in the interactions among agents a
S
and a. Considering conditions 1) and 2), if the num-
ber of occurrences of trust rating τ or its correspond-
ing possibility is 0, then TEC is also zero. Condition 3)
increases the value of TEC by increasing the number
of occurrences of trust rating τ. As observed in Con-
dition 4), if the number of observances of two trust
ratings, τ and τ
′
are equal, then the trust rating with
higher possibility is given the priority. When com-
paring the number of interactions and the possibility
value of Π
a
S
→a
(τ), the priority is given first to num-
ber of the interactions, and then, to the the possibility
value of Π
a
S
→a
(τ) in order to avoid giving preference
to the possibility values driven out of few interactions.
The following formula is an example of a TEC func-
tion which satisfies the above conditions.
TEC(τ) =
(
0, m
τ
= 0 or Π
a
S
→a
(τ) = 0
[1/(γ× m
τ
)]
(1/m
τ
)
+
Π
a
S
→a
(τ)
χ
, otherwise
where γ > 1 is the discount factor and χ ≫ 1.
Higher values of γ impede the convergence of TEC(τ)
to one and vice-versa. χ which is a very large value
insures that the influence of Π
a
S
→a
(τ) on TEC(τ) re-
mains trivial and is noticeable only when the number
of interactions are equal. In this formula, as m
τ
grows,
TEC(τ) converges to one. TEC(τ) can be utilized as a
coefficient for trust rating τ when comparing different
agents. Note that the General Case mentioned above
gives the guidelines for merging successive possibil-
ity distributions and TEC feature is only used as an
attribute when the number of interactions should be
considered and can be ignored otherwise.
6 POSSIBILITY DISTRIBUTION
OF AGENT a
S
’S TRUST IN
AGENT a
D
We propose two approaches for deriving the final pos-
sibility distribution of Π
a
S
→a
D
(τ) considering differ-
ent available possible choices.
The first approach is to consider all K possibil-
ity distributions of Π
a
S
→a
D
(τ) and take the weighted
mean of them by giving each Π
a
S
→a
D
(τ) a weight
equal to its Occurrence Probability (OP), measured
by multiplying the possibility weight of the trust val-
ues, PW(τ
i
), that are used to build Π
a
S
→a
D
(τ).
In the second approach, we only consider the trust
ratings, τ ∈ T such that Π
a
S
→a
(τ) = 1. In other words,
we only consider the trust ratings that have the high-
est weight of PW in the T
POS
a
set. Consequently, the
Π
a
S
→a
D
(τ) distributions derived from these trust val-
ues have the highest OP value which makes them
the most expected distributions. We denote by µ
a
the number of trust ratings, τ ∈ T
POS
a
that satisfy
Π
a
S
→a
(τ) = 1 for agent a. In this approach, we only
select the trust ratings in µ
a
for each agent a in A and
build the possibility distributions of Π
a
S
→a
D
(τ) out of
those trust ratings. After building M =
∏
a∈A
µ
a
differ-
ent possibility distributions of Π
a
S
→a
D
(τ), we com-
pute their average, since all of them have equal OP
weight.
Proposition 1. In both approaches, the conditions of
the general case described in the previous section are
satisfied.
Proof. Proof is omitted due to lack of space, how-
ever, it can be easily done by enumerating the differ-
ent cases.
Due to the computational burden of the first ap-
proach (which requires building K distributions of
Π
a
S
→a
D
(τ)), we used the second one in our experi-
ments as it only requires building M distributions.
To conclude this section, we would like to com-
ment on the motivation behind using possibility dis-
tribution rather than probability distributions. Indeed,
if probability distributions were used instead of pos-
sibility distributions, a confidence interval should be
considered in place of the single value of trust for
each τ in T. Consequently, for representing the prob-
ability distribution of agent a
S
’s trust in each agent
a ∈ A a confidence interval should be measured for
each τ ∈ T to consider uncertainty. The same repre-
sentation should be used for each agent a ∈ A’s trust
in a
D
. Now, in order to estimate the probability distri-
bution of agent a
D
’s trust with respect to its uncer-
tainty, we need to find some tools for merging the
ICAART 2012 - International Conference on Agents and Artificial Intelligence
186

confidence intervals of the probability distributions of
a
S
’s trust in A with the A’s trust in a
D
. To the best
of our knowledge, no work addresses this issue, ex-
cept for the following related works. In (Destercke,
2010), the number of the occurrences of each element
in the domain, which is equivalent to the number of
observance of each τ value in the interactions between
agent a and a
D
, is reported by agents in A to a
S
and
then, the probability intervals on the trust of agent a
D
is built. The work of (Campos et al., 1994) measures
the confidence intervals of a
D
’s trust out of several
confidence intervals provided by agents in A. In both
works, the manipulation of information by the agents
in A is not considered and for building the confidence
intervals of a
D
, the trust of agent a
S
in A is neglected.
Although no work addresses the trust estimation prob-
lem, we study here in the probability domain, we em-
ployed possibility distributions as they offer a flexible
and straightforward tool to address uncertainty.
7 EXPERIMENTS
We first introduce two metrics for evaluating the out-
comes of our experiments and then present the exper-
imental results.
7.1 Evaluation Metrics
Metric I - How Informative is a Possibility Distri-
bution? In the context of the possibility theory, the
uniform distribution contributes no information, as all
of the trust ratings are equally possible and cannot be
differentiated which is referred to as “complete igno-
rance” (Dubois and Prade, 1991). Consequently, the
more a possibility distribution deviates from the uni-
form distribution, the more it contributes information.
The following distribution provides the state of “com-
plete knowledge” (Dubois and Prade, 1991):
∃! τ ∈ T : Π(τ) = 1 and Π(τ
′
) = 0, ∀τ
′
6= τ, (3)
where only one trust value in T has a possibility
greater than 0. We assign an information level of 1
and 0 to distribution of 3 and the uniform distribu-
tion, respectively. In the general case, the information
level ( denoted by I) of a distribution having a total of
|T| trust ratings, is equal to:
I(Π(τ)) =
1
|T| − 1
∑
τ∈T
(1− Π(τ)). (4)
Here the distance of each possibility value of Π(τ)
from the uniform distribution is measured first for all
trust ratings of T. Then, it is normalized by |T| −
1, since at least one trust rating must be equal to 1
(property of a possibility distribution).
Metric II - Estimated Error of the Possibility Dis-
tributions: In this section we want to measure the
difference between the estimated possibility distribu-
tion of agent a
D
’s trust, as measured in Section 6,
and the true possibility distribution of a
D
’s trust. In
order to measure the true possibility distribution of
agent a
D
’s trust, the true probability distribution of
agent a
D
’s trust (which is its internal probability dis-
tribution of trust) should be transformed to a pos-
sibility distribution. Dubois et al. (Dubois et al.,
2004) provide a probability to possibility transfor-
mation tool. Through usage of their tool, the true
possibility distribution of a
D
’s trust can be measured
and then compared with the estimated distribution of
Π
a
S
→a
D
(τ). Let Π
a
S
→a
D
(τ) denote an estimated dis-
tribution, as measured in Section 6, obtained from a
fusion rule and let Π
F
(τ) represent the true possibility
distribution of a
D
’s trust transformed from its internal
probability distribution. The Estimated Error (EE) of
Π
a
S
→a
D
(τ) is measured by taking the average of the
absolute differences between the true and estimated
possibility values over all trust ratings, τ ∈ T. The EE
metric is measured as:
EE(Π
F
(τ)) =
1
|T|
∑
τ∈T
|Π
a
S
→a
D
(τ) − Π
F
(τ)|. (5)
7.2 Experimental Results
Here we perform extensive experiments to evaluate
our merging approaches. We divide the set A of agents
into three subsets. Each subset simulates a specific
level of trustworthiness in the agents. The subsets
are: A
FT
subset of Fully Trustworthy agents where
the peak of the probability trust distribution is 1, A
HT
subset of Half Trustworthy agents where the peak is
0.5 and A
NT
subset of Not Trustworthy agents where
the peak is 0. We start with A = A
NT
and gradually
move the agents from A = A
NT
to A = A
HT
such that
we reach the state of A = A
HT
where all the agents
belong to A
HT
. Later, we move agents from A = A
HT
to A = A
FT
such that we finally end up with A = A
FT
.
Over this transformation, the robustness of the esti-
mated distribution of Π
a
S
→a
D
(τ) is evaluated with re-
spect to the nature of trustworthiness of the agents.
We carry out separate experiments by changing: (1)
The number of agents in the set A, (2) The number of
interactions between each pair of agents, and (3) The
manipulationAlgorithm I and II. We intend to observe
the influence of each one of these components on the
final estimated distribution of Π
a
S
→a
D
(τ). In all ex-
periments, the number of trust rating events, |T|, is
equal to 5 (a commonly used value in most surveys).
MERGING SUCCESSIVE POSSIBILITY DISTRIBUTIONS FOR TRUST ESTIMATION UNDER UNCERTAINTY IN
MULTI-AGENT SYSTEMS
187
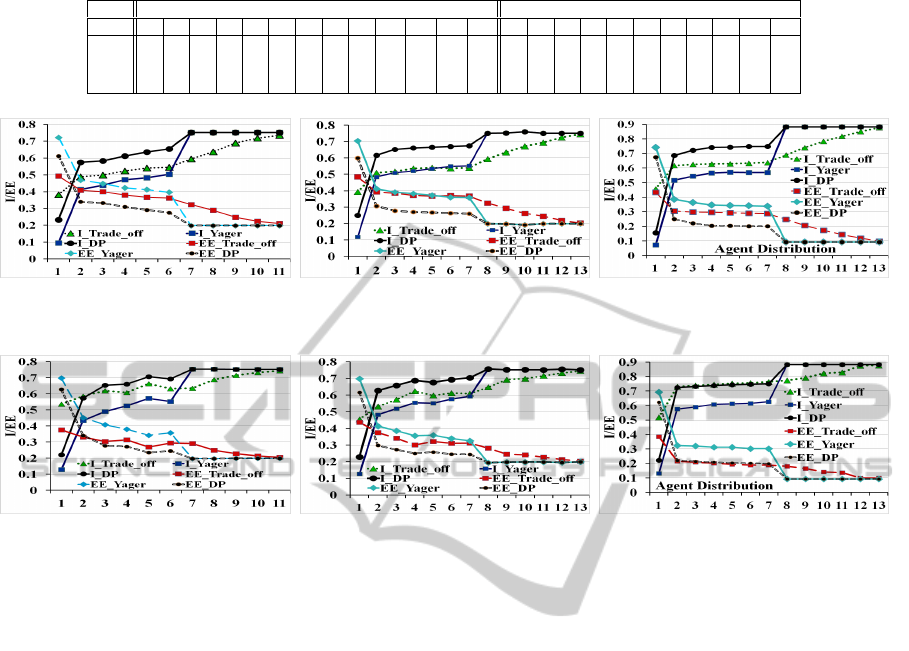
Table 1: Agent distribution corresponding to x values in Figures 2 and 3.
Agent Distribution in (b) and (c) Agent Distribution in (a)
x
1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3 4 5 6 7 8 9 10 11
|A
FT
|
0 0 0 0 0 0 0 5 10 15 20 25 30 0 0 0 0 0 0 2 4 6 8 10
|A
HT
|
0 5 10 15 20 25 30 25 20 15 10 5 0 0 2 4 6 8 10 8 6 4 2 0
|A
NT
|
30 25 20 15 10 5 0 0 0 0 0 0 0 10 8 6 4 2 0 0 0 0 0 0
(a) Agent# 10, Interaction# 20 (b) Agent# 30, Interaction# 20 (c) Agent# 30, Interaction# 50
Figure 2: Algorithm I Experiments in Different Multi-Agent Settings.
(a) Agent# 10, Interaction# 20 (b) Agent# 30, Interaction# 20 (c) Agent# 30, Interaction# 50
Figure 3: Algorithm II Experiments in Different Multi-Agent Settings.
7.2.1 Manipulation Algorithm I’s Experiments
In the first set of experiments, the manipulation algo-
rithm I is used by agents in A. Diagrams of Figure
2 represent 3 different experiments where the number
of agents in A and the interactions among the network
of agents of Figure 1(b) have changed. Table 1 gives
the distribution of agents A into A
FT
∪ A
NT
∪ A
HT
over
x axis values for Figures 2 and 3. Figure 2 demon-
strate that through migration of the agents from A
NT
to A
HT
and later to A
FT
, the Information level (I) in-
creases and the Estimated Error (EE) decreases. This
is a consequence of increase in the accuracy of infor-
mation provided by the agents in A as they become
more trustworthy.
Comparing the 3 experiments of Figure 2, increase
in the number of agents from Figures 2(a) to 2(b),
does not improve the results over high values of x,
where the number of the agents in A
FT
subset is high.
This indicates that as long as the quality of the infor-
mation reported by the agents in A does not improve,
increase in the number of the agents will not improve
the estimated distribution of Π
a
S
→a
D
(τ). However,
from x = 2 to the case where all agents are in A
HT
subset EE reduces and I increases. It indicates that
if agents are not completely trustworthy, an increase
in the number of agents increments the quality of the
estimations. Comparing Figures 2(b) and 2(c), In-
crease in the number of interactions in-between the
agents improves the results in Figure 2(c) for both I
and EE which is a consequence of higher information
exchanged between the agents. Thus, the possibility
distributions built by the agents are derived from more
information which enhances the results’ accuracy.
7.2.2 Manipulation Algorithm II’s Experiments
We repeat the same experiments with manipulation
algorithm II to observe the extent of influence of the
manipulation algorithm chosen by the set A on the fi-
nal distribution of Π
a
S
→a
D
(τ). Figure 3 represents the
results of these experiments. The graphs in Figure 2
demonstrate the same trends as algorithm I, However,
more volatility is observed in the graphs of Figure 3
compared to Figure 2 as the graphs are not monoton-
ically changing over the x axis. Indeed, this is a con-
sequence of the increased randomization of manipu-
lation algorithm II compared to algorithm I.
Comparing the fusion rules, DP outperforms other
fusion rules in all Algorithm I and II’s experiments
which is due to the fact that the DP rule is more cate-
goric in its ignorance of the agents who are not trust-
worthy compared to the 2 other fusion rules. We per-
formed additional experiments and the results show
ICAART 2012 - International Conference on Agents and Artificial Intelligence
188

that through a higher number of interactions, increase
in the trust of agents, increment of the agents’ number
in A, and decrease in the number of trust ratings (|T|),
the quality of estimation results enhances.
8 CONCLUSIONS
In this paper, we defined tools for trust estimation in
the context of uncertainty. We addressed the uncer-
tainty, arising from the empirical data that are gen-
erated from an unknown distribution, through usage
of the possibility distributions. In addition, we ana-
lyzed the properties of merging successive possibility
distributions and introduced the Trust Event Coeffi-
cient for the cases where the number of agent interac-
tions should be considered. This is the first work that
merges successive possibility distributions generated
at different levels in a multi-agent system which we
used for estimating the trust of a target agent. Fur-
thermore, we provided 2 metrics for evaluation of the
target agent’s estimated possibility distributions. We
then applied the proposed tools in intensive experi-
ments to validate our trust estimation approach.
REFERENCES
Campos, L., Huete, J., and Moral, S. (1994). Probability
intervals: a tool for uncertain reasoning. International
Journal of Uncertainty, Fuzziness and Knowledge-
based Systems, 2(2):167–196.
Delmotte, F. and Borne, P. (1998). Modeling of reliability
with possibility theory. IEEE Transactions on Sys-
tems, Man, and Cybernetics, 28:78–88.
Destercke, S. (2010). Evaluating trust from past assess-
ments with imprecise probabilities: comparing two
approaches. In Proc. of SUM, pages 151–162.
Dubois, D., Foulloy, L., Mauris, G., and Prade, H.
(2004). Probability-possibility transformations, trian-
gular fuzzy sets, and probabilistic inequalities. Reli-
able Computing, 10:273–297.
Dubois, D. and Prade, H. (1988). Possibility Theory: An
Approach to the Computerized Processing of Uncer-
tainty. Plenum Press.
Dubois, D. and Prade, H. (1991). Fuzzy sets in approximate
reasoning, part 1: inference with possibility distribu-
tions. Fuzzy Sets Syst., 40:143–202.
Dubois, D. and Prade, H. (1992). When upper probabilities
are possibility measures. Fuzzy Sets Syst., 49:65–74.
Griffiths, N. (2005). Task delegation using experience-
based multi-dimensional trust. In Proc. of AAMAS,
pages 489–496.
Huynh, T. D., Jennings, N. R., and Shadbolt, N. R. (2006).
An integrated trust and reputation model for open
multi-agent systems. In Proc. of AAMAS, 13:119–154.
Jøsang, A. (2001). A logic for uncertain probabilities. Int. J.
Uncertain. Fuzziness Knowl.-Based Syst., 9:279–311.
Masson, M.-H. and Denœux, T. (2006). Inferring a possibil-
ity distribution from empirical data. Fuzzy Sets Syst.,
157:319–340.
Ramchurn, S. D., Huynh, D., and Jennings, N. R. (2004).
Trust in multi-agent systems. The Knowledge Engi-
neering Review, 19:1–25.
Reece, S., Roberts, S., Rogers, A., and Jennings, N. R.
(2007). A multi-dimensional trust model for heteroge-
neous contract observations. In Proc. of AAAI, pages
128–135.
Sabater, J. and Sierra, C. (2001). Regret: A reputation
model for gregarious societies. In 4th Workshop on
Deception, Fraud and Trust in Agent Societies, pages
61–69. ACM.
Teacy, W. T. L., Patel, J., Jennings, N. R., and Luck, M.
(2006). Travos: Trust and reputation in the context of
inaccurate information sources. Auton. Agent Multi-
Agent Sys., 12:183–198.
Vose, D., editor (2008). Risk Analysis: A Quantitative
Guide, 3rd Edition. Wiley.
Wang, Y. and Singh, M. (2010). Evidence-based trust: A
mathematical model geared for multiagent systems.
ACM Trans. Auton. Adapt. Syst., 5:14:1–14:28.
Yager, R. (1996). On mean type aggregation. IEEE Trans-
actions on Systems, Man, and Cybernetics, 26:209 –
221.
Yager, R. R. (1987). On the dempster-shafer framework and
new combination rules. Inf. Sci., 41:93–137.
Yu, B. and Singh, M. P. (2002). An evidential model of dis-
tributed reputation management. In Proc. of AAMAS,
pages 294–301. ACM.
Zacharia, G., Moukas, A., and Maes, P. (2000). Collab-
orative reputation mechanisms for electronic market-
places. Decision Support Systems, 29(4):371 – 388.
Zadeh, L. (1965). Fuzzy sets. Information and Control,
8:338–353.
Zadeh, L. (1978). Fuzzy sets as a basis for a theory of pos-
sibility. Fuzzy Sets and Systems, 1:3–28.
MERGING SUCCESSIVE POSSIBILITY DISTRIBUTIONS FOR TRUST ESTIMATION UNDER UNCERTAINTY IN
MULTI-AGENT SYSTEMS
189
