
OPTIMIZATION TOOLS ADRESSING FUZZY UNCERTAINTY
AT POWER FLOWS
Preparation of Camera-Ready Contributions to SciTePress Proceedings
Eduardo M. Gouveia
1
and Paulo Moisés Costa
1,2
1
School of Technology and Management, Polytechnic Institute of Viseu, Campus Poliécnico de Repeses, Viseu, Portugal
2
INESC Porto, Porto, Portugal
Keywords: Power Flow, Fuzzy, Symmetric, Optimization.
Abstract: Power flow studies use computational tools for the planning and operation of electrical power systems
purposes. The deterministic model is the most commonly used load flow approach. In this model, the input
data and the results are crisp values. Therefore, to account for uncertainties, the most common approach
used is the definition of scenarios, which are characterized by crisp values. This is an impractical way to
solve the problem of the uncertainty in the data. A more practical way to lead with the uncertainties is the
use of probabilistic power flows. On such approach, the uncertainties are modelled through the use of
probability density functions (pdf). However, that approach may be inappropriate, namely when there is no
available historical data in order to construct the pdf. On such cases, the fuzzy power flows (FPF) is an
interesting alternative. In this paper, a methodology named Symmetric Fuzzy Power Flow is used. That
methodology uses optimization models to solve power flow problems considering the uncertainty treated as
fuzzy numbers. A comparison between the proposed methodology and the classic ones is also provided.
1 INTRODUCTION
Power flows is one of the most used tools to support
the planning and operation activities of the
transmission network. There are two main classes of
power flows considering uncertainty, the
probabilistic power flow (PPF) (Borkowska, 1974)
and the fuzzy power flow (FPF) (Miranda and
Matos, 1989; Saraiva et al., 1991). In the PPF the
variables (generation and load) are considered as
random variables with probabilistic distributions
(pdf). The results of PPF are also in the form of pdf,
namely the voltages and power flows. This model
presupposes the existence of historical data for the
input variables that can guarantee the construction of
a statistical distribution. However, the historical data
may not be available, namely when we are leading
with emergent concepts as the generation at LV
networks and the electric mobility. Therefore, new
tools are needed in order to solve the problem
resulting from the inexistence of historical data. The
FPF is an interesting alternative on such context,
once this approach treats the uncertainty without
requiring the existence of statistical distributions for
the input data. The FPF, allows describe
mathematically qualitative statements or vague
information by using fuzzy models. The classic
formulations of FPF present some limitations that
may distort the results, namely: i) existence of a
slack bus (which aggregates all uncertainty that
comes from the all other buses of the transmission;
ii) linearization models used at the computation.
Saraiva el al, 2004 presented a model that includes
data correlation. An inclusion of a corrective
procedure for the slack bus is purposed by (Saraiva
et al, 1991), which consists in defining limits for
generation. In this situation, the slack bus still being
different from the others buses since continues to
receive the uncertainty from them.
In this paper a symmetrical model (SFPF)
purposed by Matos and Gouveia (2008) is used in
order to overcome some of the limitations of the
preceding models. In fact, the slack bus is treated as
all other buses and non linearization procedures are
adopted. The proposed model uses optimization
problems to obtain symmetrical solutions for the
power flow problem (regarding linearized and the
complete model). The main purpose of the paper is
to analyse the results of the SFPF and compare those
results with the ones of classic versions of the FPF.
219
M. Gouveia E. and Moisés Costa P..
OPTIMIZATION TOOLS ADRESSING FUZZY UNCERTAINTY AT POWER FLOWS.
DOI: 10.5220/0003760502190222
In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 219-222
ISBN: 978-989-8425-97-3
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
The paper is organized in the following way:
Section 2 - concepts of FPF and SFPF are reviewed;
section 3 - three case studies are presented (the IEEE
test grids with 14, 24 and 118 buses are used);
section 4 - some conclusions are extracted.
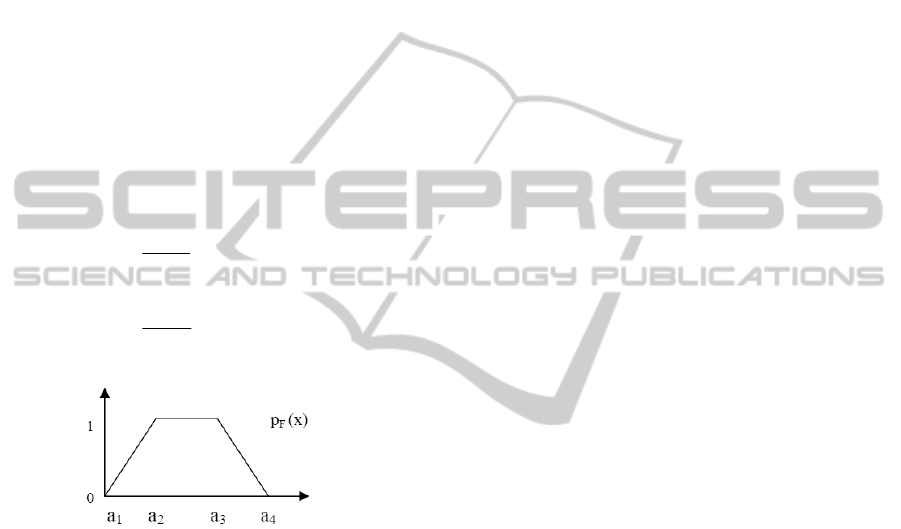
2 FUZZY POWER FLOW
There are three types of fuzzy numbers generally
used in FPF to describe input data at fuzzy power
flow models: rectangular, triangular and trapezoidal.
Triangular and rectangular fuzzy numbers are
particular cases of trapezoidal fuzzy numbers.
Triangular and rectangular fuzzy numbers are
particular cases of trapezoidal fuzzy numbers. For
instance, a trapezoidal fuzzy number (Figure 1) can
be described by the set of equations (1).
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
≥
≤≤
−
−
≤≤
≤≤
−
−
≤
=
4
43
34
4
32
21
12
1
1
,0
,
,1
,
,0
)(
axif
axaif
aa
xa
axaif
axaif
aa
ax
axif
xp
F
(1)
Figure 1: Trapezoidal Fuzzy Number.
2.1 Classical Fuzzy Power Flow
The first formulation of Fuzzy Power Flow was
based on a DC model for the power system. In this
model if
P
~
is the fuzzy vector of injected power in
the nodes. an approximation of the arguments,
θ
~
and
branches’ flows
B
P
~
, is obtained using:
PAP
B
~
.
~
=
(2)
PB
~
.
~
1−
=
θ
(3)
At these model, crisp matrices A and B corresponds
to the sensitivity and admittance matrices of the DC
power flow.
The AC model of FPF was proposed by Miranda
et al (1990). This model uses a first-order Taylor
series expansion of the power flow equations. To
obtain the fuzzy voltages and angles a deterministic
AC power flow for the central values of the fuzzy
data is solved, using the Newton-Raphson algorithm.
Then, the variations around this operating point are
calculated by using the Jacobian of the last iteration
and fuzzy arithmetic’s. For other variables like the
power flows, a similar strategy of linearization is
used. More details about this model can be found in
Miranda el al (1990).
2.2 Symmetric Fuzzy Power Flow
The SFPF consists of solve for each α level of the
possibility distribution (Figure 1), optimization
problems in order to obtain the maximum and
minimum value that fuzzy variable may take, for all
the possible values (with degree of membership
greater than or equal to α). Note that no slack bus is
defined since fuzzy injections for input data are
considered for all the buses of the transmission
network. For the DC model of SFPF (Matos and
Gouveia, 2008) we must solve linear programming
problems (for each α level) to obtain the maximum
value of the power flow in branch k. At this model
(4), “Ref” means the reference bus and
()
α
i
P
~
is the
α-level interval of the nodal active injected power. If
is desired the injected power at a specific bus, the
objective function will be
()
α
i
P
~
.
(
)
()
∑
∑
=
∈
=
≠
i
i
ii
Refi
ikik
P
ibusesallPPst
PAP
0
~
:
.
~
max
α
α
(4)
Gouveia and Matos (2008) also extend the SFPF to
the AC case. Now the standard equations of the AC
power flow problem are included as constraints,
along with the α-limits for each fuzzy variable. The
maximum α-level value for each fuzzy variable
Z
~
will be the result of following optimization
problem (5). The analysis for the minimum is
analogous. Variable Z may be any of the voltages in
PQ buses, any of the voltage angles, any of the
power flows
P
ik
, Q
ik
or S
ik
or the power losses in a
branch or in the entire system. In (5),
G
ik
and B
ik
are,
respectively, the real and imaginary components of
the admittance matrix elements,
()
α
i
P
~
is the α-level
interval of the active injected power
i
P
~
and
(
)
α
i
Q
~
is
the α-level interval of the reactive injected power
i
Q
~
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
220
()
()
()
0
~
~
)cossin(
)sincos(:
~
max
Ref
1
1
=
=
∈
∈
−=
+=
∑
∑
=
=
θ
α
α
θθ
θθ
α
RefandbusesPVVV
ibusesallQQ
ibusesallPP
ibusesallBGVVQ
ibusesallBGVVPst
Z
SP
ii
ii
ii
ikikikik
n
k
kii
ikikikik
n
k
kii
(5)
3 CASE STUDY
In this section we will perform the exercise of
comparing the results obtained from SFPF with the
ones available at the literature obtained by the
classical FPF.
3.1 Linear Models of FPF
Three different models were used to solve the power
flow problem (DC model) for the 24 Bus, 38
branches IEEE test system: the first model of FPF
created by Miranda and Matos (1989); the model
with correction procedures which consider
generations limits to the slack bus (Saraiva et al,
1991); and the SFPF (Gouveia and Matos, 2008).
Those models are indentified in the following
paragraphs and figures as “First”, “Cons” and
“Sym”. We will consider the uncertainty modelled
as trapezoidal fuzzy numbers (triangular or
rectangular fuzzy numbers also could be used). The
values indicated in Table I will be considered the
central values of the trapezoidal fuzzy numbers. For
these data the characteristic points are assumed to be
as shown at Table 2. For instance, applying this
information to node 9, we’ll get a fuzzy load of
(Figure 2). A base power of 500 MW is used and
bus and branch data are available at (Saraiva et al,
1991); The bus 1 is the reference bus.
0
0.2
0.4
0.6
0.8
1
-340 -330 -320 -310 -300 -290
MW
Possib.
P9
Figure 2: Fuzzy load.
The voltages for PV buses 1, 2 and 7 will be 1.075
pu and for the others 1.025 pu. At the reference bus,
depending on the model we will have different
situations: “First”- no fuzzy description for
generation is considered; “Cons” – were considered
generation limits of [0-800 MW]; “Sym” is defined
a fuzzy generation. In this fuzzy trapezoidal number
the extreme points (a
1
, a
2
, a
3
, a
4
) will be (0, 500, 600,
800) MW. After solving the optimization problem
(4) twice (max and min) for α cuts between 0 and 1
for all branches with large branch limitations we
obtain the ranges for the P
i-k
power flows. For
instance for branch 1-2 (Table 2, Figure 3) the main
points of interest of the possibility distribution are
referred (α=0
-
, α=0.7
-
, α=1
-
, α=1
+
, α=0
+
). Figure 4
show the same kind of results for branch 5-10. As
can be verified formulations “First” and “Const”
provides results with larger ranges of uncertainty for
power flows since slack bus concentrates all
uncertainty which comes from all other buses.
Table 1: Characteristic points of fuzzy data.
Bus characteristic points for generation
1-13, 14-24 0.95 0.98 1.02 1.05
13 1.00 1.00 1.00 1.00
characteristic points for loads
1-5, 7-19,
21-24
0.95 0.98 1.02 1.05
6, 20 1.00 1.00 1.00 1.00
Table 2: Power flow fuzzy distributions, branch 1-2
(MW).
Branch
0 0.7 1 1 0
1-2 (First)
-68.0 11.2 45.1 196.1 309.2
1-2
(Const)
-68.0 11.2 45.1 196.1 245.3
1-2 (Sym)
-68.0 18.9 85.2 147.2 245.3
0
0.2
0.4
0.6
0.8
1
-100 -20 60 140 220 300 380 460
MW
Poss.
P1-2 Fir st
P1-2 Cons .
P1-2 Sy m.
Figure 3: Fuzzy load flow in branch 1-2.
0
0.2
0.4
0.6
0.8
1
-80 -30 20 70 120 170 220
MW
Poss.
P5-10 First
P5-10 Cons.
P5-10 Sy m.
Figure 4: Fuzzy load flow in branch 5-10.
OPTIMIZATION TOOLS ADRESSING FUZZY UNCERTAINTY AT POWER FLOWS
221

3.2 Complete Models of FPF
Now we will perform the exercise of comparing AC
SFPF with classical AC FPF models. Considering
the model based on FPF, the boundary load flow
(BLF) (Dimitrovski and Tomsovic, 2004) we will
use the IEEE 14 and 118 test systems. Data of these
networks can be seen at (http://www.ee.washington
.edu/research/pstca/. The BLF uses an interactive
procedure in order to enhance the results accuracy in
cases of considerable non linearity due to large
uncertainty in input data. The characteristic points
for IEEE 14 bus test system at α=0 are assumed to
be 0.0 and 2.0 of the central values (rectangular
fuzzy numbers). Performing the comparison with the
exact values calculated with the SFPF shows that
some “artificially uncertainty” is still present in the
BLF results. Table 3 shows results for voltage
magnitudes. The same kinds of results (not shown)
were also obtained for active power flows. Using the
118 bus test system also Gouveia and Matos (2008)
found differences between the FPF, BLF (that falls
under same philosophy of FPF) and SFPF. Those
differences are exposed for some of the variables of
this network (Table 4). Now the characteristic points
for α=0 are assumed to be 0.6 and 1.4 of the central
values.
Table 3: Voltage values (pu) IEEE 14 bus test system.
α=0, [0.0-2.0]
Bus BLF SFPF AC
4 0.978 1.045 0.992 1.045
5 0.981 1.042 0.996 1.042
7 1.024 1.089 1.051 1.088
9 1.001 1.101 1.028 1.101
10 0.997 1.096 1.020 1.096
11 1.025 1.084 1.038 1.083
12 1.036 1.072 1.039 1.072
13 1.023 1.074 1.028 1.074
14 0.972 1.089 0.992 1.088
Table 4: Voltage and Power Flow Values (p.u.) for some
variables of IEEE 118 test system.
Var. FPF BLF Sym. FPF
V44 0.94 1.03 0.87 1.01 0.96 1.01
P68-69 -17.44 14.92 -21.10 13.27 -3.74 1.39
Q68-69 0.39 1.86 0.84 9.25 1.07 1.33
4 CONCLUSIONS
The use of SFPF doesn’t consider a slack bus or
linearization procedures as happens at the traditional
formulation of FPF. At FPF the use of these
simplifications have as a consequence a distortion of
the results mainly due the influence of the slack bus.
While in the deterministic power flow formulations
the slack bus only compensate the uncertainty in loss
estimation, at classical FPF compensates the
uncertainty that comes from all other buses. Adding
to this the linearization procedures used, results
shown “excessive” uncertainty as shown in this
paper at the several IEEE networks tested. Finally,
the SFPF models have the drawback of requiring
solving a great number of optimization problems but
are completely symmetric regarding the buses. This
is not a real problem since SFPF are addicted to
long-term planning studies. However justify future
work in order to improve simulation times.
REFERENCES
Borkowska, B., 1974. Probabilistic load flow. IEEE
Transactions on PAS 23 (3), 752– 759.
Dimitrovski A, Tomsovic K, 2004. Boundary Load Flow
Solutions, IEEE Trans. Power Systems, vol. 19, no.1,
February 2004, pp 348-355.
Gouveia E M, Matos M A, 2008 ”Symmetric AC Fuzzy
Power Flow Model”, European Journal of Operational
Research, DOI: 10.1016/j.ejor.2007.12.044”
Matos M A, Gouveia E M, 2008. Fuzzy Power Flow
Revisited, Power Systems, IEEE Transactions on,
Volume 23, Issue 1, Page(s):213 – 218, February 2008
Miranda, V., Matos, M. A., 1989. Distribution system
planning with fuzzy models and techniques. In:
Proceedings of the CIRED 89, Brighton, pp. 472–476
Miranda, V., Matos, M. A., Saraiva, J. T., 1990. Fuzzy
load flow - new algorithms incorporating uncertain
generation and load representation. In: Proceedings of
the 10th PSCC, London, pp. 621–627
Saraiva, J T, Fonseca N, Matos M A, 2004. Fuzzy Power
Flow – An AC Model Addressing Correlated Data, in:
Proc PMAPS’04, Iowa, September 2004, pp 519-524.
Saraiva, J. T., Miranda, V., Matos, M. A., 1991.
Generation and load uncertainties incorporated in load
flow studies. In: Proceedings of the MELECON 91,
424 Ljubljana, pp. 1339-1342
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
222
