
OPTIMIZED ALGORITHM FOR LEARNING BAYESIAN
NETWORK SUPER-STRUCTURES
Edwin Villanueva and Carlos Dias Maciel
Department of Electrical Engineering, Sao Carlos School of Engineering, University of Sao Paulo, Sao Paulo, Brazil
Keywords:
Bayesian networks, Structure learning, Super-structure.
Abstract:
Estimating super-structures (SS) as structural constraints for learning Bayesian networks (BN) is an important
step of scaling up these models to high-dimensional problems. However, the literature has shown a lack of
algorithms with an appropriate accuracy for such purpose. The recent Hybrid Parents and Children - HPC
(De Morais and Aussem, 2010) has shown an interesting accuracy, but its local design and high computational
cost discourage its use as SS estimator. We present here the OptHPC, an optimized version of HPC that
implements several optimizations to get an efficient global method for learning SS. We demonstrate through
several experiments that OptHPC estimates SS with the same accuracy than HPC in about 30% of the statistical
tests used by it. Also, OptHPC showed the most favorable balance sensitivity/specificity and computational
cost for use as super-structure estimator when compared to several state-of-the-art methods.
1 INTRODUCTION
A Bayesian Network (BN) is a powerful tool for rep-
resenting complex probabilistic knowledge. It have
been broadly applied in a variety of fields (Pourret
et al., 2008). The knowledge in a BN is intuitively
represented via a directed acyclic graph DAG (model
structure), where nodes represent domain variables
and edges represent dependencies between them.
The main difficulty in building a BN is the induc-
tion of its structure from data. A wealth of litera-
ture has been produced for this end with two domi-
nant approaches: the constraint-based (CB) and the
score-and-search (SS). In the CB approach, the struc-
ture is found via conditional independence (CI) tests.
In the SS approach, the network is found by optimiz-
ing a function that measures how well the network
fits the data. Both approaches have drawbacks. CB
methods are inaccurate in dense networks with lim-
ited data because CI tests become unreliable in such
cases. SS methods are more accurate, but they do not
scale up to high-dimensional problems due to a super-
exponential growth of the search space (Wang et al.,
2007). Hybrid methods have emerged to overcome
these limitations (Wong and Leung, 2004; Tsamardi-
nos et al., 2006; Perrier et al., 2008; Kojima et al.,
2010). In this approach, an undirected graph (super-
structure) is estimated first with a CB approach, which
is then used in a subsequent SS phase as structural
constraints, i.e., the final structure is searched consid-
ering only edges on the super-structure.
Despite the expected gain in scalability and ac-
curacy with the hybrid approach, some concerns has
been raised regarding the need of specialized methods
to estimate super-structures (Perrier et al., 2008; Ko-
jima et al., 2010). Indeed, most available CB meth-
ods were designed for one of two purposes: either
they were made to get the exact skeleton (as the PC
(Spirtes et al., 2000)) or they were made to get a local
network around a variable of interest (as MMPC and
GetPC (Tsamardinos et al., 2006; Pena et al., 2007)).
The problem is that those methods do not control ac-
tively the rate of false-negative errors (FNE) when
the assumptions in which they rely are not more valid
(limited-data cases). Controlling the FNE rate of the
super-structure estimation is key in a hybrid approach,
since it will be the FNE rate of the whole learning
process (Perrier et al., 2008). The recent Hybrid Par-
ents and Children - HPC algorithm (De Morais and
Aussem, 2010) was proposed to lower the FNE rate
in a local context (it gets the parents and children of a
variable). HPC has shown an interesting FNE reduc-
tion in limited-data, while being correct in the sample
limit. Unfortunately, such reduction comes at an in-
creased computational cost. Also, a direct use of it as
super-structure learner would lead to repetitions in CI
tests, increasing more the computational cost, which
could undermine the benefits of the hybrid approach.
217
Villanueva E. and Maciel C. (2012).
OPTIMIZED ALGORITHM FOR LEARNING BAYESIAN NETWORK SUPER-STRUCTURES.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 217-222
DOI: 10.5220/0003785402170222
Copyright
c
SciTePress

In this paper we present the Optimized Hybrid
Parents and Children (OptHPC), an optimized ver-
sion of HPC for tasks of super-structure estimation.
The optimizations were done in order to get a global
method and to lower the computational cost of HPC,
while maintaining the precision of it. Among the opti-
mizations are: the use of a cache to store dependence
calculations of zero and first order and the use of a
global structure to consult/store detected zero-first-
order CIs. OptHPC is compared against representa-
tive state-of-the-art algorithms, including the HPC,
the MMPC, the GetPC, and the Heuristics PC (He-
uPC) (Wang et al., 2007). Results from several bench-
mark datasets show OptHPC as a promising super-
structure estimator in the hybrid learning approach.
2 BACKGROUND
A BN (Pearl, 1988) is a model hG, Θi for represent-
ing the joint probability distribution P over a set of
random variables U = {X
1
,... ,X
n
}. G is a directed
acyclic graph - DAG (the model structure) whose
nodes have a one-to-one correspondence to the ran-
dom variables in U (reason why nodes and variables
are used indistinctly) and edges represent conditional
dependence relationships among variables. Θ is a set
of parameters that define for each node X
i
a condi-
tional probability distribution (conditioned on the par-
ents of X
i
). All BN satisfies the Markov condition
(MC) (Pearl, 1988): every node X
i
is conditionally in-
dependent on any subset of its non-descendants given
its parents Pa
i
. A BN is said to be faithful with re-
spect to a distribution P if the MC applied on its DAG
G entails all and only the CIs in P. A faithful distri-
bution P is one for which exists a faithful BN hG, ·i;
G is called a perfect map of P. In this paper we as-
sume faithful distributions to be learned, so the struc-
ture learning problem is the induction of a DAG G
from a statistical sample D (following distribution P)
that is a perfect map of P (Perrier et al., 2008). We use
X⊥Y |Z to denote that variables X and Y are CI given
a variable set Z. The order of a CI is the cardinality of
the conditioning set. The set of parents and children
of a node X is denoted by PC
X
, the set of spouses by
SP
X
and the Markov blanket by MB
X
.
3 OPTIMIZED HYBRID PARENTS
AND CHILDREN - OptHPC
The main disadvantage of HPC as super-structure
learner is its local design. For instance, when HPC
is run on a variable T , many tests are performed to
check CIs of the form T ⊥X|Z. When HPC is run
latter on X , some CI tests involving T (in the form
X⊥T |Z) are performed again. These repetitions could
be painful in high-dimensional problems, since CI
tests are expensive operations. OptHPC overcomes
such limitation by using 2 global structures: i) a cache
C to store/recover computed degrees of dependency
of zero and first order; and ii) a global graph
˙
G to
store and get detected CIs of zero and first order (the
absence of a link between nodes X,Y in
˙
G indicates
X⊥Y |Z, |Z| < 2). Only computations of zero and first
order are stored in cache because they are the largest
portion of CIs in common problems. Also, if higher
orders computations are cached, the complexity and
time delays of the cache could be significantly exac-
erbated. The structure
˙
G serves as a fast means to
save/consult CIs of zero and first order detected along
the execution of the algorithm. We do not represent
higher order CIs in
˙
G for simplicity and because they
are less reliable when data is limited.
Algorithm 1: OptHPC.
input : D (dataset, samples of random vars. U)
output: S (super-structure)
1 S = (U,
/
0) // Init. super-structure
2
˙
G = (U,U × U) // Init. 0-1-order graph
3 C
hX,Y i
=
/
0, ∀(X—Y ) ∈
˙
G // Init. cache
4 for all T ∈ U do
5 [PC
T
,
˙
G,C ] = HPC*(T,D,
˙
G,C )
6 for all X ∈ PC
T
do S = S + (T —X)
OptHPC has the same subroutines than HPC, but
optimized to work with the new structures
˙
G, C (we
rename them by appending * to the original names,
i.e., HPC*, DE-PCS*, DE-SPS* and Inter-IAPC*).
The main procedure (Algorithm 1) constructs the
super-structure S by calling successively the modi-
fied HPC* on each system variable. C and
˙
G are
passed to HPC* in each call.
˙
G is initialized with
a fully-connected graph (edges are removed as CIs
are detected). In contrast, super-structure S is initial-
ized without edges (they are added with each return of
HPC*, line 6). The CI testing is carried out through
the function Dep. It computes from dataset D the de-
gree of dependence between variables X and Y given
set Z, dep
X,Y |Z
. If such degree is lower than a thresh-
old α (significance level) a 0 is returned indicating
X⊥Y |Z. If |Z| < 2 the resulting degree is added to
the cache C ; specifically to the entry C
hX,Y i
, which is
a dictionary that save computed degree of dependen-
cies relative to variables X and Y (the key is the con-
ditioning variable Z and the value is dep
X,Y |Z
). Each
required degree of dependence of zero or first order is
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
218

Algorithm 2: HPC*.
input : T (target); D (dataset);
˙
G and C
output: PC
T
; updated
˙
G and C
1 [
˙
G,C ] = DE-PCS*(T,D,
˙
G,C )
2 [
˙
G,C ] = DE-SPS*(T,D,
˙
G,
˙
G)
3 PCS
T
= Ad j(T,
˙
G); SPS
T
= Sps(T,,
˙
G)
4 U
T
= T ∪ PCS
T
∪ SPS
T
5 [PC
T
,
˙
G,C ] = Inter-IAPC*(T,D,U
T
,
˙
G,C )
6 for all X ∈ PCS
T
\ PC
T
do
7 [PC
X
,
˙
G,C ] = Inter-IAPC*(X, D,U
T
,
˙
G,C )
8 if T ∈ PC
X
then PC
T
= PC
T
∪ X
Algorithm 3: DE-PCS*.
input : T (target); D (dataset);
˙
G and C
output: updated
˙
G and C
// Remove edge T —X from
˙
G if T ⊥X
1 for all X ∈ Ad j(T,
˙
G) do
2 [dep,C ] = Dep(T,X ,
/
0,D, C )
3 if dep = 0 then
˙
G =
˙
G − (T —X)
// Remove T —X from
˙
G if T ⊥X|Y
4 for all X ∈ Ad j(T,
˙
G) do
5 Ad
T
= Ad j(T,
˙
G); Ad
X
= Ad j(X,
˙
G)
6 if Ad
T
\ X =
/
0 or Ad
X
\ T =
/
0 then continue
7 B
1
= Ad
T
∩ Ad
X
; B
2
= Ad
T
\ B
1
; B
3
= Ad
X
\ B
1
8 for i = 1 to 3 do
9 for all Y ∈ B
i
do
10 [dep,C ] = Dep(T,X ,Y,D,C )
11 if dep = 0 then
12
˙
G =
˙
G − (T —X); break 2 loops
first checked in the respective cache entry.
HPC* (Algorithm 2) computes the parents and
children (PC) of a target variable by using the same
basic steps than HPC. However, differently from it,
HPC* works in a global context, placing the results of
zero-first-order CI testing in the cache C and structure
˙
G to be available along successive calls to it. Subrou-
tine DE-PCS* (Algorithm 3) is called by HPC* to get
a superset of PC (SPC) for a target T . DE-PCS* puts
its result in
˙
G instead of returning it explicitly (as in
DE-PCS). The SPC is recovered in HPC* by look-
ing the target’s adjacency in
˙
G (with function Ad j),
which avoids repeated computations. Other optimiza-
tions in DE-PCS* are: i) (line 6) prevent the search
for d-separators on edges T —X with T or X being a
leaf node (node whose unique adjacency is the other
edge node), since such edges cannot be separated; and
ii) start the search for separators in the common ad-
jacency of the edge nodes, and then in the remain-
ing adjacency (lines 7-12). This in practice speeds up
the finding of separators, since they (if any) are more
likely to be in the common edge adjacency. Subrou-
tine DE-SPS* (Algorithm 4) is called by HPC* to get
Algorithm 4: DE-SPS*.
input : T (target); D (dataset);
˙
G and C
output: updated
˙
G and C
1 for all X ∈ Ad j(T,
˙
G) do
2 Ad
X
= Ad j(X,
˙
G); Ad
T
= Ad j(T,
˙
G)
3 Sp
X
T
= Sps(T,X ,
˙
G)
4 for all Y ∈ Ad
X
\ {T ∪ Ad
T
∪ Sp
X
T
} do
5 sep = Sep(T,X,C )
6 if sep = X then continue
7 [dep,C ] = Dep(T,Y,X ∪ Sep, D,C )
8 if dep 6= 0 then // make T → X ← Y
9
˙
G =
˙
G − {(X → T ),(X → Y )}
10 for all Y ∈ Sps(T,X,
˙
G) do
11 for all Z ∈ Sps(T,X,
˙
G) \Y do
12 [dep,C ] = Dep(T,Y,X ∪ Z, D,C )
13 if dep = 0 then // restore X ↔ Y
14
˙
G =
˙
G + (X → Y ); break
Algorithm 5: Inter-IAPC*.
input : T (target); D (data); U
T
(variables);
˙
G; C
output: PC
T
; updated
˙
G and C
1 MB
T
=
/
0
2 repeat
// Add true positives to MB
T
3 for all X ∈ {U
T
\ MB
T
\ T } do
4 [dep
X
,C ] = Dep(T,X ,MB
T
,D, C )
5 if dep
X
= 0 and |MB
T
| < 2 then
6
˙
G =
˙
G − (T —X)
7 if max
X
(dep
X
) = 0 then break
8 MB
T
= MB
T
∪ argmax
X
(dep
X
)
// Remove false positives from MB
T
9 for all X ∈ MB
T
do
10 [dep,C ] = Dep(T,X ,MB
T
\ X,D, C )
11 if dep = 0 then
12 MB
T
= MB
T
\ X
13 if |MB
T
| < 2 then
˙
G =
˙
G − (T —X)
14 until MB
T
has not changed
15 if |MB
T
| < 2 then return
// Remove spouses of T from MB
T
16 PC
T
= MB
T
17 for all X ∈ MB
T
do
18 [ f sep, sep,C ] = FindSep(T,X,PC
T
\ X,D, C )
19 if f sep = true then
20 PC
T
= PC
T
\ X
21 if |sep| < 2 then
˙
G =
˙
G − (T —X)
a superset of spouses (SPS) for a target T . As in DE-
PCS*,
˙
G is used as the working object. The SPS is
recovered from
˙
G in HPC* with function Sps (when
passed a second argument X to it, only the target’s
spouses with child X are returned, as in lines 3,10-
11 in DE-SPS*). Whenever a possible v-structure
T → X ← Y is detected (i.e. when Y becomes de-
OPTIMIZED ALGORITHM FOR LEARNING BAYESIAN NETWORK SUPER-STRUCTURES
219

pendent on T given the current separator and X ) it is
reflected in
˙
G by orienting the respective edges (lines
7-9). In a second phase (lines 10-14) all created v-
structures T → X ← Y are reviewed: if any variable
Y is found as ancestor or descendant of another tar-
get’s spouse, it is considerate as non-spouse and the
bi-directionality of edge Y → X is restored (line 14).
Inter-IAPC* (Algorithm 5) is a procedure called by
HPC* to get an initial candidate PC set for a tar-
get variable T . Inter-IAPC* works only on the set
U
T
formed by parents, children and spouses of T re-
turned by DE-PCS* and DE-SPS*, which save com-
putations.
˙
G and C are also used/updated whenever a
zero-first-order CI test is required. However, as Inter-
IAPC* uses higher order CI testing, the final result
is worked on the internal set PC
T
: first, the Markov
blanket of the target T is obtained (lines 2-14) and
then the target’s spouses are identified and removed
from it (lines 15-21). Function FindSep is used to
assist that identification (line 18). It looks for a sub-
set Z ⊆ Z that makes T and X CI. If found, a flag
f sep is returned as ”true” along with the found Z (in
sep), otherwise f sep is returned as ”false”. To save
computations, we restrict Z to the current shrinking
PC set (PC
T
\ X}) instead of the whole MB
T
(as in
Inter-IAPC). This is justified because spouse separa-
tors always can be found in the true PC set (which is
in the current PC
T
). Another optimization is in line
7, where the search of the MB
T
is ended as soon as
no new candidates exist to enter to it.
4 EXPERIMENTAL EVALUATION
The accuracy and computational cost of OptHPC is
compared against some representative state-of-the-art
algorithms for skeleton recovery, including the HPC,
the MMPC (with all optimizations of the original
paper), the Heuristics PC (its original name is algo-
rithmHPC, but in this paper we call it as HeuPC to
avoid confusion with HPC) and the GetPC. Accuracy
is assessed by the sensitivity (Sn = T P/(T P + FN))
and specificity (Sp = T P/(T P + FP)) indices (Pena
et al., 2007), where T P is the number of edges
correctly estimated, FN is the number of missing
edges (false negatives), and FP is the number of
extra edges. Computational cost is assessed by the
number of statistical calls (NSC) used to get the
answer. NSC is a fair estimate of the computational
efficiency of CB methods, since they spend most
of the time doing statistical tests (Tsamardinos
et al., 2006). NSC is also independent from the
computing platform. Four known benchmark BNs
were used for the accuracy evaluation: Alarm,
Child, Insurance and Haildfinder. They were chosen
to have increasing complexity cases (Alarm has
37 nodes, 46 edges, domain range DR=[2-4] and
maximum indegree MI=6; Child has 20 nodes,
25 edges, DR=[2-6] and MI=8; Insurance has 27
nodes, 52 edges, DR=[2-5] and MI=9; Hailfinder
has 56 nodes, 66 edges, DR=[2-11] and MI=17). All
datasets were taken from the repository at www.dsl-
lab.org/supplements/mmhc paper/mmhc index.html
released by the authors of the MMPC. We choose
for each network 15 datasets: 5 with 500 instances,
5 with 1000 instances and 5 with 5000 instances.
For the NSC evaluation, we use additionally datasets
sampled from tiled versions of the above networks
(in the same repository). Tiling is a procedure
to construct networks with larger dimensionality
by joining several copies of an original network
(Tsamardinos et al., 2006). We choose tiling of 3,
5 and 10. All indices are averaged for the same
network and sample size. Due to the need of a
common platform to make fair comparisons, only
author’s own implementations of the studied algo-
rithms were used. Every effort was taken to match
our implementation to the originals. All algorithms
perform the CI testing through function Dep in order
to standardize the NSC counting. G
2
is used as the CI
test statistics (α = 0.05) (Tsamardinos et al., 2006).
It is not performed if there are less than 5 samples
on average per cell; in that case independence is
assumed (Tsamardinos et al., 2006).
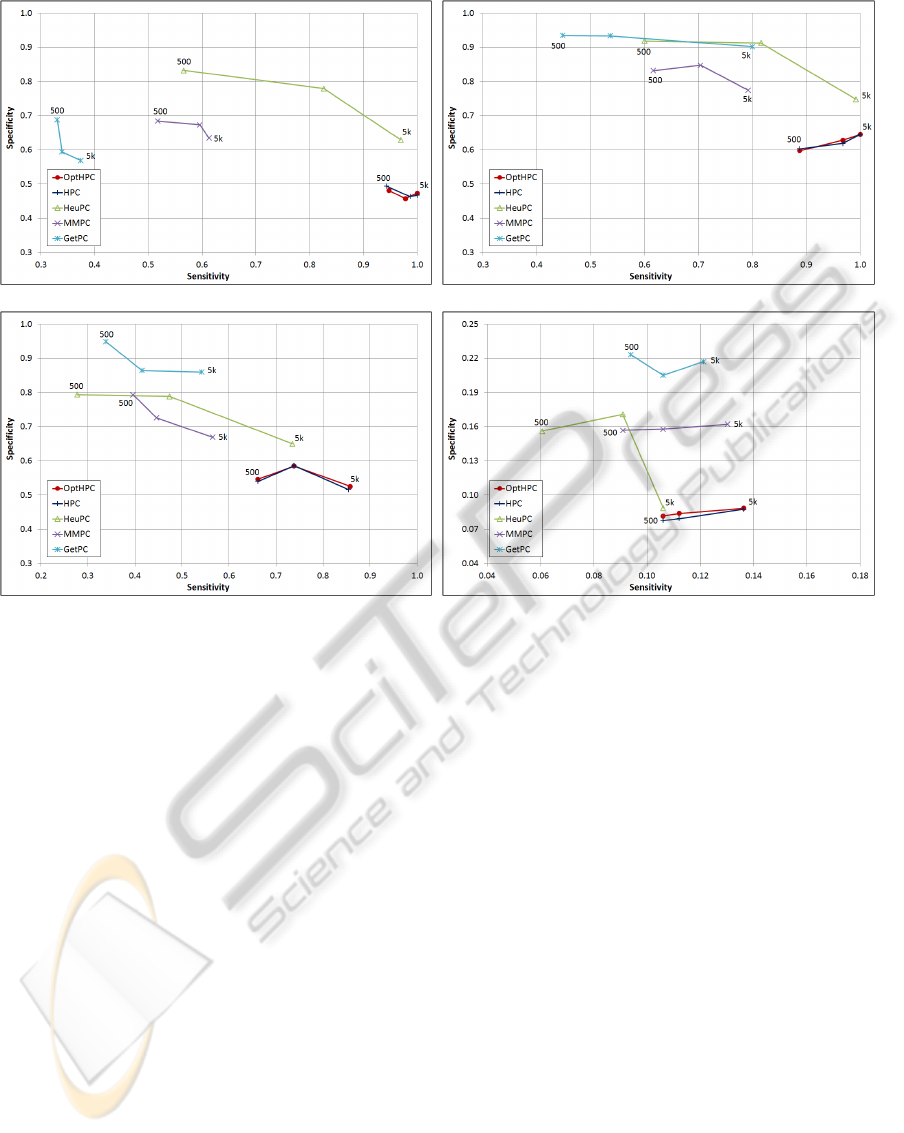
Figure 1 shows the sensitivity and specificity val-
ues obtained in the 4 networks. Each curve represents
an algorithm, where the points correspond to the dif-
ferent sample sizes. It is observed that OptHPC and
HPC have very close values in all cases, which con-
firm that the optimizations in OptHPC do not alter the
accuracy of HPC. All algorithms increment the sensi-
tivity with the sample size, as expected, but OptHPC
and HPC have values markedly higher than the other
in all networks and sample size (more noticeably in
small sample size). They, in fact, reach the maximum
sensitivity in the simplest networks (Alarm and Child)
at sample size 5000. Contrasting with the sensitivity,
OptHPC and HPC have the lowest specificity in all
networks. This means that more false-positive edges
are included in the final structure. However, from the
viewpoint of BN hybrid learning, such false-positive
increment is of lesser importance than having a good
sensitivity. This because the sensitivity of the whole
learning process is upper-bounded by the sensitivity
of the super-structure estimation phase (since no false
negatives can be corrected there), while the specificity
can be improved in the SS phase (Wang et al., 2007).
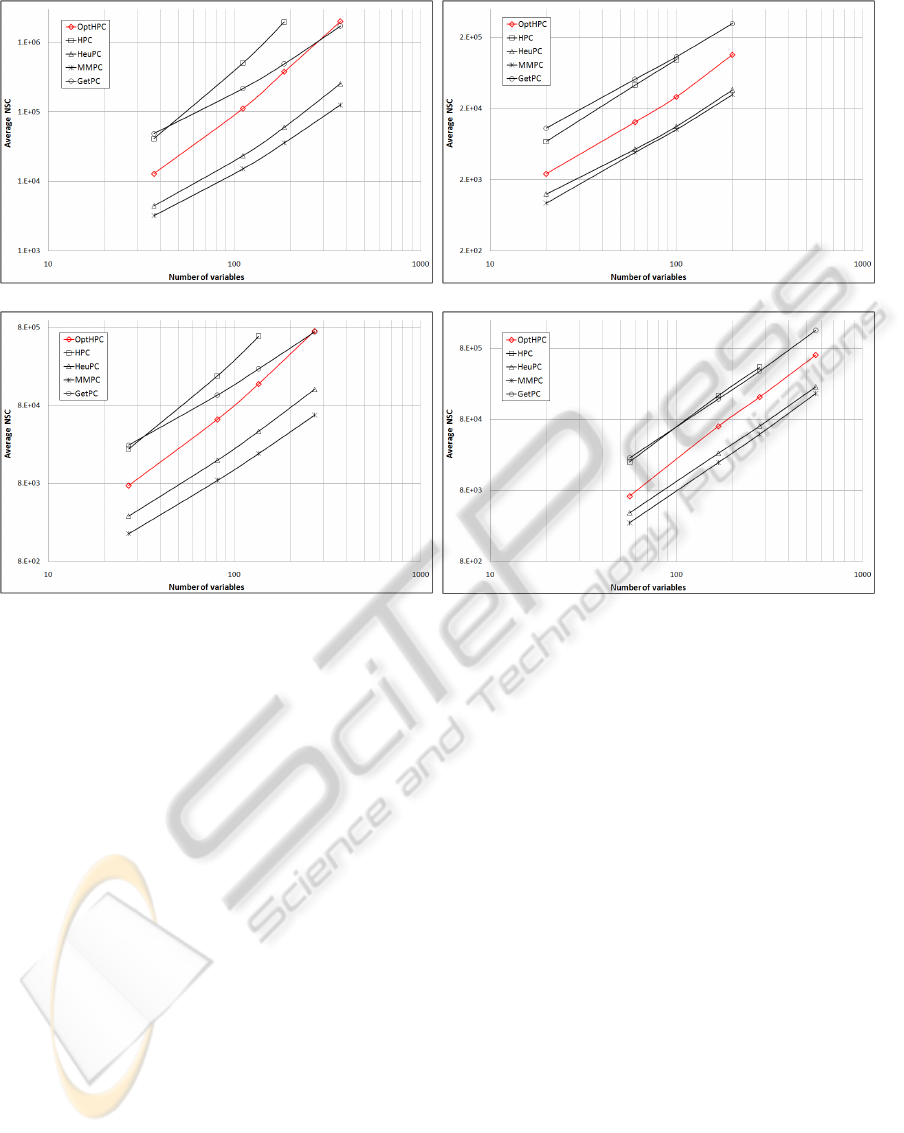
Figure 2 shows the obtained NSC values. Each
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
220
(a) Alarm (b) Child
(c) Insurance (d) Hailfinder
Figure 1: Results for sensitivity and specificity indices. The points in the curves (algorithms) correspond to the average values
of sensitivity and specificity for the different sample sizes (results for datasets of 500 and 5000 instances are indicated).
subfigure present results for an original network and
its corresponding tiled versions. The points in the
curves (algorithms) were plotted in the correspond-
ing dimensionality of the (original or tiled) network
and the obtained NSC value (averaged over all sam-
ple sizes in the corresponding network). Logarithmic
scales are used due to large differences in the results.
Values for HPC in networks with tiling 10 are not
shown because it took longer time than our imposed
tolerance (30 hours single CPU). It can be observed
that HPC and GetPC have the highest NSC values
among all algorithms, although GetPC has a better
scalability to higher dimensions. OptHPC presents a
pronounced reduction of the NSC values in all net-
works with respect to HPC, representing in average
about 30% of the NSC used by it. HeuPC and MMPC
have the lowest NSC values, but they have a discour-
aging sensitivity/specificity balance for applications
in the hybrid learning approach.
5 CONCLUSIONS
In this paper we presented an optimized version of the
recent HPC algorithm, an algorithm for learning the
parents and children of a target variable that showed
an attractive accuracy for the BN hybrid learning ap-
proach. The new algorithm, called OptHPC, imple-
ments several optimizations to get an efficient global
method for such approach. Results in benchmark
datasets showed that OptHPC is effective in reducing
the computational cost of HPC, needing on average
30% of the statistical tests used by it without loss of
accuracy. Compared to some representative skeleton-
recovery algorithms, OptHPC showed the most suit-
able balance sensitivity/specificity and computational
cost for use as super-structure estimator in the hybrid
learning approach. We are currently testing OptHPC
coupled in a whole hybrid system to asses at what ex-
tent the total learning time is reduced.
ACKNOWLEDGEMENTS
We would like to acknowledge support for this project
from the brazilian government agency CAPES.
OPTIMIZED ALGORITHM FOR LEARNING BAYESIAN NETWORK SUPER-STRUCTURES
221
(a) Alarm (b) Child
(c) Insurance (d) Hailfinder
Figure 2: Results for the NSC index. Each subfigure shows results from datasets corresponding to the same network (including
its tiled versions). The points in the curves (algorithms) were plotted in the corresponding dimensionality of the network and
the NSC value (averaged over all sample sizes in that network). Logarithmic scales are used in both axes.
REFERENCES
De Morais, S. R. and Aussem, A. (2010). An efficient
and scalable algorithm for local bayesian network
structure discovery. In European conference on Ma-
chine learning and knowledge discovery in databases:
Part III, ECML PKDD’10, pages 164–179. Springer-
Verlag.
Kojima, K., Perrier, E., Imoto, S., and Miyano, S. (2010).
Optimal search on clustered structural constraint for
learning bayesian network structure. J. Mach. Learn.
Res., 11:285–310.
Pearl, J. (1988). Probabilistic reasoning in intelligent sys-
tems. Morgan Kaufmann.
Pena, J. M., Nilsson, R., Bjorkegren, J., and Tegner, J.
(2007). Towards scalable and data efficient learning
of Markov boundaries. Int. J. Approx. Reasoning,
45(2):211–232.
Perrier, E., Imoto, S., and Miyano, S. (2008). Finding Op-
timal Bayesian Network Given a Super-Structure. J.
Mach. Learn. Res., 9:2251–2286.
Pourret, O., Nam, P., Na
¨
ım, P., Marcot, B., and Na?m, P.
(2008). Bayesian Networks: A Practical Guide to Ap-
plications. Statistics in Practice. John Wiley & Sons.
Spirtes, P., Glymour, C., and Scheines, R. (2000). Causa-
tion, prediction, and search. The MIT Press, Cam-
bridge, second edition.
Tsamardinos, I., Brown, L. E., and Aliferis, C. F. (2006).
The max-min hill-climbing Bayesian network struc-
ture learning algorithm. Mach. Learn., 65(1):31–78.
Wang, M., Chen, Z., and Cloutier, S. (2007). A hybrid
Bayesian network learning method for constructing
gene networks. Comput. Biol. Chem., 31(5-6):361–
372.
Wong, M. and Leung, K. (2004). An efficient data min-
ing method for learning Bayesian networks using an
evolutionary algorithm-based hybrid approach. IEEE
Trans. Evol. Comput., 8(4):378–404.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
222
