
MULTI-LEVEL DYNAMIC MODELING IN BIOLOGICAL SYSTEMS
Application of Hybrid Petri Nets to Network Simulation
Rafael S. Costa
1,3
, Daniel Machado
1
, A. R. Neves
2
and Susana Vinga
3,4
1
IBB-Institute for Biotechnology and Bioengineering, University of Minho, Campus de Gualtar, 4710-057 Braga, Portugal
2
ITQB/UNL, R. Qta Grande 6, 2781-901 Oeiras, Portugal
3
Instituto de Engenharia de Sistemas e Computadores, Investigac¸
˜
ao e Desenvolvimento (INESC-ID),
R. Alves Redol 9, 1000-029 Lisboa, Portugal
4
FCM-UNL, C. Martires P
´
atria 130, 1169-056 Lisboa, Portugal
Keywords:
Systems biology, Integrated dynamic modelling, Hybrid Petri net, Approximate rate laws, Streptococcus
pneumoniae.
Abstract:
The recent progress in the high-throughput experimental technologies allows the reconstruction of many bi-
ological networks and to evaluate changes in proteins, genes and metabolites levels in different conditions.
On the other hand, computational models, when complemented with regulatory information, can be used to
predict the phenotype of an organism under different genetic and environmental conditions. These computa-
tional methods can be used for example to identify molecular targets capable of inactivating a bacterium and
to understand its virulence factors. This work proposes a hybrid metabolic-regulatory Petri net approach that
is based on the combination of approximate enzyme-kinetic rate laws and Petri nets. A prototypic network
model is used as a test-case to illustrate the application of these concepts in Systems Biology.
1 INTRODUCTION
Living cell systems are complex networks with dif-
ferent kinds of interacting chemical compounds (e.g.
genes, small molecules and proteins). The interac-
tions with each other propagate through the global
network and the understanding of how a system be-
havior emerges is a major aim of the recent field of
science called Systems Biology (Kitano, 2002). Un-
derstanding the mechanisms of the cell is essential for
research in several areas such as drug design with ap-
plications to personalized medicine (Zhu et al., 2008),
identification potential drug targets (Lee et al., 2009)
and metabolic engineering (Park et al., 2007).
By using mathematical models of cellular
metabolism, it is possible to systematically test and
predict the optimal environmental and genetic manip-
ulations (Di Ventura et al., 2006). The availability
of genome sequences for many microorganisms has
allowed the development of constraint-based models
representing the global network of metabolic reac-
tions (Price et al., 2003). However, while captur-
ing most mass balance effects, those models ignore
regulation and cannot be used for dynamic simula-
tions. Moreover, applying constraint based methods
directly to integrated networks is challenging (Covert
et al., 2008). Ideally, the models would comprise
different levels of knowledge, from reactions stoi-
chiometry to reactions kinetics and regulatory infor-
mation (e.g. transcriptional and enzymatic regulation)
(Klipp, 2007). This is the basis of the E-Cell project
(Tomita et al., 1999), that uses an approach to repre-
sent the dynamic state inside the whole cell. Although
until recently most cellular components have been
studied individually, the behavior of the cell emerges
at the network-level interactions and requires an inte-
grative analysis. Several models and analysis focused
primarily on isolated network models rather than in-
tegrated systems. Examples of this are the analy-
sis of signaling (Hoffmann et al., 2002), metabolic
(Chassagnole et al., 2002) and regulation (Lee et al.,
2002) systems. Thus, it is highly desirable that in-
formation obtained from genome annotation, together
with kinetic and regulatory information can be used
for the construction of integrated models that account
for various interactions at diverse temporal and spatial
scales.
Petri nets are a mathematical formalism that have
been applied in the modeling of several biological
pathway systems (Chaouiya et al., 2004; Chen et al.,
2007; Zevedei-Oancea et al., 2003). Hybrid Petri
nets are a particular type of Petri net extension devel-
317
S. Costa R., Machado D., R. Neves A. and Vinga S..
MULTI-LEVEL DYNAMIC MODELING IN BIOLOGICAL SYSTEMS - Application of Hybrid Petri Nets to Network Simulation.
DOI: 10.5220/0003785503170321
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 317-321
ISBN: 978-989-8425-90-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
oped to accomodate discrete and continuous elements
within the same formalism. This makes them spe-
cially appealing for the integration of gene regulatory
and metabolic networks, that are more commonly rep-
resented as Boolean networks and differential equa-
tions, respectively. This idea was explored in (Chen
and Hofestadt, 2003) to build a regulated metabolic
model of the urea cycle, and also in (Doi et al., 2004)
to reconstruct the glycolytic pathway controlled by
the lac operon.
The recent advent of so-called genome-wide high-
throughput methods have generated the called omics
data (e.g. metabolomics, proteomics, transcriptomics
and genomics) of bio-molecules like mRNA, proteins
and metabolites, the detection of molecular interac-
tions, such as, protein-DNA and protein-metabolite
(Nielsen and Olsson, 2002). This has allowed a bet-
ter understanding of the regulation of metabolism at
a global scale (Lee et al., 2005). However, in spite
of the great advances in the area, we are still far from
a whole-cell computational model that integrates dif-
ferent omics data, as there exists a few approaches
for the model-driven interpretation of these data and
models that couple enzymatic and transcriptional reg-
ulation (Bettenbrock et al., 2006; Kotte et al., 2010;
Tenazinha and Vinga, 2011; Usuda et al., 2010; Patil
and Nielsen, 2005).
The main aim of this work is the creation of an
integrating framework for metabolic and regulatory
modeling of biological systems, including how we ad-
dress some challenges in integrated systems. This pa-
per is organized as follows: Section 1 explores the
state of the art and the motivation for the work; Sec-
tion 2 presents a hybrid kinetic modeling framework
and Section 3 discusses their application to a proto-
typic small network. Section 4 discusses remaining
challenges and our future directions.
2 METHODS
2.1 Model Topology
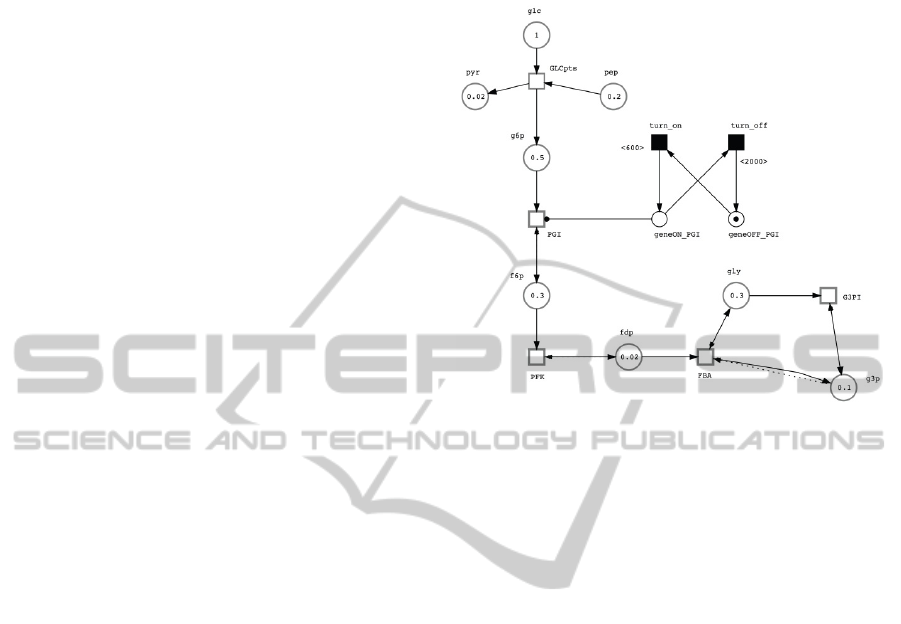
In order to evaluate the proposed approach we used as
an example the model topology shown in Figure 1. It
comprises some of the glycolysis reactions for Strep-
tococcus pneumoniae retrieved from the draft model
reconstruction using the SEED web-tool (Henry et al.,
2010) and information from KEGG (Ogata et al.,
1999) database. The biochemical interactions of these
reactions have been translated into the Petri net model
used in this work. The network consists of 5 contin-
uous transitions representing the reactions; 8 continu-
ous places representing 8 metabolites; and 2 discrete
places and 2 discrete transitions were used to create
the regulatory components (on/off switch).
Figure 1: Hybrid Petri net representation of the prototypic
metabolic-regulatory network buit with the Snoopy sofware
tool (Rohr et al., 2010). The metabolites are represented
by circles (places) and the enzymes by squares (transi-
tions). Metabolites abbreviations: pyr, pyruvate; pep, phos-
phoenolpyruvate; glc, glucose; g6p, glucose-6-phosphate;
f6p, fructose-6-phosphate; fdp, fructose-1,6-bisphosphate;
gly, glycine; g3p, glucose-3-phosphate. Enzymes abbre-
viations: GLCpts, phosphotransferase of PTS system (EC
2.7.3.9); PGI, glucose-6-phospate isomerase (EC 5.3.1.9);
PFK, phosphofructokinase (EC 2.7.1.11); FBA, fructose-
bisphosphate aldolase (EC 4.1.2.13); G3PI, triosephosphate
isomerase (EC 5.3.1.1).
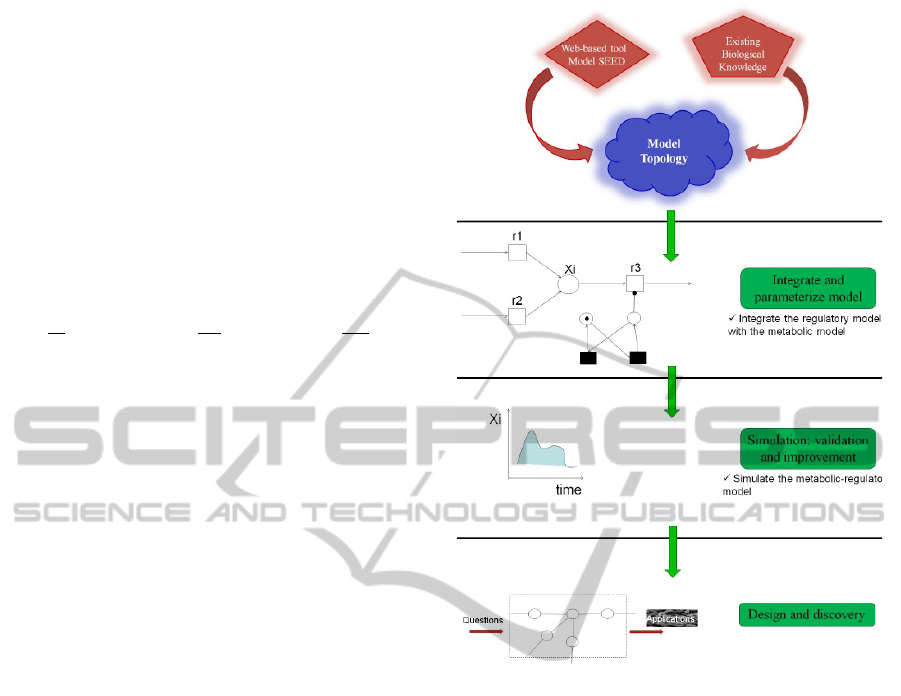
2.2 Modeling Process
The overall idea of the modeling method is depicted
in Figure 2. After the model topology construction,
it is necessary to translate into mathematical differen-
tial equations and introduce the control of regulatory
events. In this study, we use an extension of the orig-
inal formalism known as hybrid Petri nets (Hassane
and David, 1998) that accounts for metabolite dy-
namics coupled gene regulation and enzyme kinetics
to construct the hybrid metabolic-regulatory model.
The metabolic network is represented with continu-
ous places and continuous transitions. Genes are rep-
resented by discrete places. Each gene is represented
by two places (on and off), which are connected to
transitions that activate and inactivate the gene, ensur-
ing that the activation of both places is mutually ex-
clusive. The connection between both layers is made
by means of activation arcs between the reactions and
the respective genes. The Petri net model of the net-
work was drawn using the graphical editor of the Petri
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
318
net tool Snoopy (Rohr et al., 2010). Snoopy is a gen-
eral purpose software application for design and sim-
ulation of graph-based formalisms and is freely avail-
able.
Recently, we have studied several types of approx-
imate enzyme-kinetic rate laws (Costa et al., 2010).
In this study, approximate kinetics lin-log representa-
tions are used for the rate equations, but alternatively
other approximate rate laws (e.g convenience kinet-
ics) can be also integrated. Lin-log kinetics (Visser
and Heijnen, 2003) are formulated based on a refer-
ence rate r
0
, and given by:
r = r
0
e
e
0
1 +
n
S
∑
i
ε
0
S
i
ln
S
i
S
i
0
+
n
P
∑
j
ε
0
P
j
ln
P
j
P
j
0
!
(1)
where the superscripts (
0
) denote the reference
state (e.g. wild type at steady-state), r
0
is the refer-
ence reaction rate value, e/e
0
represent the relative
enzyme activities, S
i
/S
0
i
and P
j
/P
0
j
are the relative
concentrations that influence the kinetics of the reac-
tion.
The negative of the corresponding stoichiometric
coefficients were set as the initial guesses for the elas-
ticities parameter values as suggested by (Smallbone
et al., 2007). The initial concentrations of metabo-
lites were taken as arbitrary values and are assuming
that the reference steady-state is known (pyr = 0.02
mM; pep = 0.2 mM; glc, = 1 mM; g6p = 0.5 mM;
f6p = 0.3 mM; fdp = 0.02 mM; gly = 0.3 mM; g3p
= 0.1 mM). The simulation process of the metabolic-
regulatory model performed in this study, were car-
ried out using the Snoopy tool (Rohr et al., 2010).
3 ILLUSTRATION OF A
PROTOTYPIC NETWORK
Computational models are very useful for exploring
the effects of manipulating pathways through drugs.
The aim of this study was to present an approach to
construct a hybrid mathematical kinetic model that
accounts for the metabolic and regulatory events.
This approach was applied by taking the small pro-
totypic integrated system of S. pneumoniae (shown in
Figure 1) as an example.
In Figure 3a and 3b simulation time courses of
all the metabolite concentration show the effect of a
gene activation with and without the regulation part,
respectively.
We demonstrated how inclusion of regulatory
events may affect the phenotype behavior. As an ex-
ample of this changes, at time = 600 seconds the pgi
Figure 2: Overview of the modeling process from the con-
struction of a biochemical reaction network to conversion
into a mathematical format. (1) SEED web-based soft-
ware is used to reconstruct the metabolic network includ-
ing the metabolic part and the regulatory information are
based on existing biological knowledge. (2) Conversion of
the metabolic network to a computational model. Combin-
ing the regulatory events and the metabolic information in
a hybrid Petri net modeling framework. (3) Modeling and
simulation in Snoopy tool (Rohr et al., 2010). (4) Model
application example: identify essential genes encoding new
targets for antibacterial drugs that can be tested in vitro for
reduction of pathogenicity.
gene is activated and the affect on the dynamical be-
haviour of the g6p, f6p, fdp, gly and g3p metabolites
are shown, reaching a new steady state a time = 1100
seconds (3a). Our results show that regulation has
influence on the steady-state distribution obtained in
comparison with the model without the regulation ef-
fect. Accounting for these regulations may have a sig-
nificant impact in the phenotype predictions and can
reveal new therapeutic targets.
MULTI-LEVEL DYNAMIC MODELING IN BIOLOGICAL SYSTEMS - Application of Hybrid Petri Nets to Network
Simulation
319
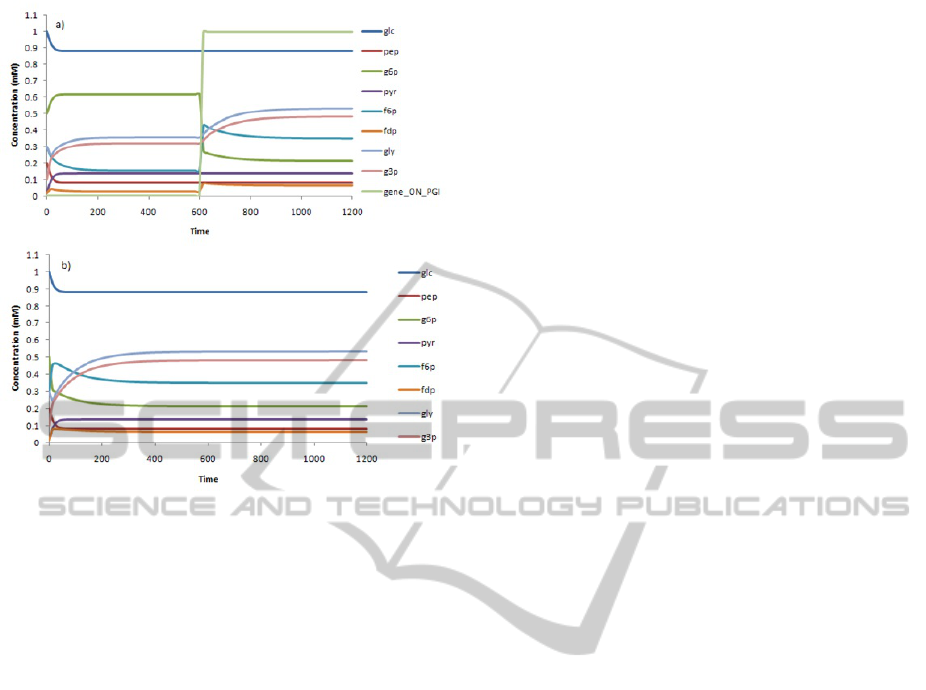
Figure 3: Simulation of the dynamics for the prototypic S.
pneumoniae model with the pgi gene activation after 600s
(a) and without accounting regulatory effects (b). The inte-
grated system, comprise metabolic and regulation events.
4 CONCLUSIONS AND FUTURE
WORK
This work presents a strategy to build a hybrid
metabolic-regulatory model based on a Petri net
framework. This work addresses also the impact of
accounting of a kind of regulation which comes from
gene regulation. This approach has significant advan-
tages, because the model design and analysis is easily
connected between the continuous and discrete fea-
tures that would otherwise be unforeseen. Moreover,
it can reveal insights into disease mechanism and pos-
sible therapeutic targets with applications to health.
On the other hand, there are still some current
problems in our proposed modeling approach that
need to be addressed. The kinetic parameter val-
ues estimation is a significant bottleneck. Here we
use the negative of the stoichiometry from each reac-
tion for the parameters as suggested by (Smallbone
et al., 2007). However a natural attempt is to distin-
guish kinetic parameters for the discrete and continu-
ous events of the hybrid model. In order to estimate
the kinetic parameters of the metabolic reactions, the
proposed procedure is to isolate the metabolic net-
work and perform parameter fitting using experimen-
tal data (metabolites and fluxes time course data) on
a short time scale for which the genetic part can be
considered constant. For this purpose, in the future it
is intended to use experimental steady-state and time-
course metabolomic and fluxomic data from S. pneu-
moniae that will be generated by other participants
in the PneumoSyS project. This experimental data
will be also used for model validation. Another lim-
itation is that the metabolic reconstructions obtained
from the SEED tool do not account for the regulatory
interactions. Therefore, it will be necessary to anno-
tate the model topology reconstruction with such in-
formation, which can be obtained from available liter-
ature and web-databases. An additional challenge of
integrated modeling approaches are time scales. For
example, metabolic reactions occur on the order of
seconds. By contrast, regulatory reactions can take
several minutes to hours.
In future work, we intend develop and vali-
date a complete dynamic hybrid metabolic-regulatory
model of S. pneumoniae using the proposed approach
to predict disease-related metabolic states, which is of
major bio-medical interest.
ACKNOWLEDGEMENTS
This work was partially supported by post-doctoral
grant by Fundac¸
˜
ao para a Ci
ˆ
encia e a Tecnolo-
gia (FCT) (SFRH/BPD/80784/2011), project Pneu-
moSyS - A Systems Biology approach to the role
of pneumococcal carbon metabolism in colonization
and invasive disease (FCT contract: PTDC/SAU-
MII/100964/2008) and by FCT (INESC-ID multian-
nual funding) through the PIDDAC Program funds.
REFERENCES
Bettenbrock, K., Fischer, S., Kremling, A., Jahreis, K.,
Sauter, T., and Gilles, E. (2006). A quantitative ap-
proach to catabolite repression in Escherichia coli.
Journal of Biological Chemistry, 281:2578.
Chaouiya, C., Remy, E., Ruet, P., and Thieffry, D. (2004).
Qualitative modelling of genetic networks: From log-
ical regulatory graphs to standard Petri nets. Applica-
tions and Theory of Petri Nets 2004, pages 137–156.
Chassagnole, C., Noisommit-Rizzi, N., Schmid, J., Mauch,
K., and Reuss, M. (2002). Dynamic modeling of
the central carbon metabolism of Escherichia coli.
Biotechnology and Bioengineering, 79(1):53–73.
Chen, L., Qi-Wei, G., Nakata, M., Matsuno, H., and
Miyano, S. (2007). Modelling and simulation of sig-
nal transductions in an apoptosis pathway by using
timed Petri nets. Journal of biosciences, 32(1):113–
127.
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
320

Chen, M. and Hofestadt, R. (2003). Quantitative petri net
model of gene regulated metabolic networks in the
cell. In silico biology, 3(3):347–365.
Costa, R., Machado, D., Rocha, I., et al. (2010). Hybrid dy-
namic modeling of Escherichia coli central metabolic
network combining Michaelis-Menten and approxi-
mate kinetic equations. Biosystems, 100(2):150–157.
Covert, M., Xiao, N., Chen, T., and Karr, J. (2008). Inte-
grating metabolic, transcriptional regulatory and sig-
nal transduction models in Escherichia coli. Bioinfor-
matics, 24(18):2044–2050.
Di Ventura, B., Lemerle, C., Michalodimitrakis, K., and
Serrano, L. (2006). From in vivo to in silico biology
and back. Nature, 443(7111):527–533.
Doi, A., Fujita, S., Matsuno, H., Nagasaki, M., and Miyano,
S. (2004). Constructing biological pathway models
with hybrid functional petri nets. In silico biology,
4(3):371–291.
Hassane, A. and David, R. (1998). Continuous and hybrid
Petri nets. Journal of Circuits Systems and Computers,
8:159–188.
Henry, C., DeJongh, M., Best, A., Frybarger, P., Linsay, B.,
and Stevens, R. (2010). High-throughput generation,
optimization and analysis of genome-scale metabolic
models. Nature biotechnology, 28(9):977–982.
Hoffmann, A., Levchenko, A., Scott, M., and Baltimore,
D. (2002). The iκb-nf-κb signaling module: tem-
poral control and selective gene activation. Science,
298(5596):1241.
Kitano, H. (2002). Systems biology: a brief overview. Sci-
ence, 295(5560):1662.
Klipp, E. (2007). Modelling dynamic processes in yeast.
Yeast, 24(11):943–959.
Kotte, O., Zaugg, J., and Heinemann, M. (2010). Bacterial
adaptation through distributed sensing of metabolic
fluxes. Molecular Systems Biology, 6(1).
Lee, D., Saha, R., Yusufi, F., Park, W., and Karimi, I.
(2009). Web-based applications for building, man-
aging and analysing kinetic models of biological sys-
tems. Briefings in bioinformatics, 10(1):65–74.
Lee, S., Lee, D., and Kim, T. (2005). Systems biotechnol-
ogy for strain improvement. TRENDS in Biotechnol-
ogy, 23(7):349–358.
Lee, T., Rinaldi, N., Robert, F., Odom, D., Bar-Joseph,
Z., Gerber, G., Hannett, N., Harbison, C., Thompson,
C., Simon, I., et al. (2002). Transcriptional regula-
tory networks in Saccharomyces cerevisiae. Science,
298(5594):799.
Nielsen, J. and Olsson, L. (2002). An expanded role for mi-
crobial physiology in metabolic engineering and func-
tional genomics: Moving towards systems biology1.
FEMS yeast research, 2(2):175–181.
Ogata, H., Goto, S., Sato, K., Fujibuchi, W., Bono, H., and
Kanehisa, M. (1999). KEGG: Kyoto encyclopedia of
genes and genomes. Nucleic acids research, 27(1):29.
Park, J., Lee, K., Kim, T., and Lee, S. (2007). Metabolic
engineering of Escherichia coli for the production of
l-valine based on transcriptome analysis and in sil-
ico gene knockout simulation. Proceedings of the na-
tional academy of sciences of the USA, 104(19):7797.
Patil, K. and Nielsen, J. (2005). Uncovering transcriptional
regulation of metabolism by using metabolic network
topology. Proceedings of the national academy of sci-
ences of the USA, 102(8):2685.
Price, N., Papin, J., Schilling, C., and Palsson, B.
(2003). Genome-scale microbial in silico models: the
constraints-based approach. TRENDS in Biotechnol-
ogy, 21(4):162–169.
Rohr, C., Marwan, W., and Heiner, M. (2010). Snoopy - a
unifying Petri net framework to investigate biomolec-
ular networks. Bioinformatics, 26(7):974.
Smallbone, K., Simeonidis, E., Broomhead, D., and Kell,
D. (2007). Something from nothing- bridging the gap
between constraint-based and kinetic modelling. Febs
Journal, 274(21):5576–5585.
Tenazinha, N. and Vinga, S. (2011). A survey on meth-
ods for modeling and analyzing integrated biological
networks. IEEE/ACM Transactions on Computational
Biology and Bioinformatics (TCBB), 8(4):943–958.
Tomita, M., Hashimoto, K., Takahashi, K., Shimizu, T.,
Matsuzaki, Y., Miyoshi, F., Saito, K., Tanida, S., Yugi,
K., Venter, J., et al. (1999). E-CELL: software en-
vironment for whole-cell simulation. Bioinformatics,
15(1):72–84.
Usuda, Y., Nishio, Y., Iwatani, S., Van Dien, S., Imaizumi,
A., Shimbo, K., Kageyama, N., Iwahata, D., Miyano,
H., and Matsui, K. (2010). Dynamic modeling of Es-
cherichia coli metabolic and regulatory systems for
amino-acid production. Journal of biotechnology,
147(1):17–30.
Visser, D. and Heijnen, J. (2003). Dynamic simulation and
metabolic re-design of a branched pathway using lin-
log kinetics. Metabolic Engineering, 5(3):164–176.
Zevedei-Oancea, I., Schuster, S., et al. (2003). Topologi-
cal analysis of metabolic networks based on Petri net
theory. In silico biology, 3(3):323–345.
Zhu, J., Zhang, B., and Schadt, E. (2008). A systems biol-
ogy approach to drug discovery. Advances in genetics,
60:603–635.
MULTI-LEVEL DYNAMIC MODELING IN BIOLOGICAL SYSTEMS - Application of Hybrid Petri Nets to Network
Simulation
321
