
FINDING NEW EASI ECG COEFFICIENTS
Improving EASI ECG Model using Various Regression Techniques
Wojciech Oleksy and Ewarystk Tkacz
Silesian University of Technology, Gliwice, Poland
Keywords: EASI, ECG, Multilayer perceptron, SMO, Artificial neural network, Linear regression, Pace regression.
Abstract: Main idea of this study was to increase efficiency of the EASI ECG method introduced by Dover in 1988
using various regression techniques. EASI was proven to have high correlation with standard 12 lead ECG.
Apart from that it is less susceptible to artefacts, increase mobility of patients and is easier to use because of
smaller number of electrodes. Multilayer Perceptron (Artificial Neural Network), Support Vector Machine
Regression (with Sequential Minimal Optimization algorithm), Linear Regression and Pace Regression
methods were used to improve the quality of the 12-lead electrocardiogram derived from four (EASI)
electrodes. Hundreds of ANNs with different learning rates and number of hidden layers were built and
tested using data from PhysioNet and also data that were artificially generated. Next SMO Regression
method with few different kernels (polynomial, normalized polynomial and RBF), Linear Regression and
Pace Regression method were tested on the same dataset. All computed results were compared with those
obtained using classic EASI ECG method described by Dover. Computation of Root Mean Squared Error
and Correlation Coefficient was performed to measure the overall result of a given method. Obtained results
show that various regression methods could be used to increase the performance of EASI ECG method and
thus make it more popular.
1 INTRODUCTION
In 1988 Dower and his team introduced EASI ECG
system, which derives standard 12 lead ECG using
only 5 electrodes. The E electrode is on the sternum
while, the A and I electrodes are at the left and right
mid-auxiliary lines, respectively. The S electrode is
at the sternal manubrium. The fifth electrode is a
ground and is typically placed on one or the other
clavicle, see Fig 1. EASI was proven to have high
correlation with standard 12 lead ECG, as well as
with Mason-Likar 12-Lead ECG. Apart from that it
is less susceptible to artifacts, it increase mobility of
patients, it is easier and faster to use because of
smaller number of electrodes. What is more, smaller
number of electrodes reduces cost of a device. The
electrodes are positioned over readily identified
landmarks which can be located with minimal
variability, independent of the patient’s physique,
assuring high repeatability. The electrode placement
make the chest largely unencumbered, allowing
physical or imaging examination of the heart and
lungs without removing the electrodes.
2 PROBLEM DESCRIPTION
In the classical approach introduced by Dower,
using the EASI lead configuration, 3 modified
vectorcardiographic signals are recorded from the
following bipolar electrode pairs:
- A-I (primarily X, or horizontal vector component)
- E-S (primarily Y, or vertical vector component)
- A-S (containing X, Y, plus Z, the anteriorposterior
component)
Each of the 12 ECG leads is derived as a weighted
linear sum of these 3 base signals using the
following formula:
L
derive
= a(A – I) + b(E – S) + c(A – S) (1)
where L represents any surface ECG lead and a, b,
and c represent empirical coefficients. These
coefficients, developed by Dower, are positive or
negative values, accurate to 3 decimal places, which
result in leads very similar to standard leads.
Our idea to improve EASI ECG performance
was to find new model used for 12 ECG leads
calculation. To do that we treated the system as a
black box with 4 input variables: E, A, S, I and 12
406
Oleksy W. and Tkacz E..
FINDING NEW EASI ECG COEFFICIENTS - Improving EASI ECG Model using Various Regression Techniques.
DOI: 10.5220/0003788404060409
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 406-409
ISBN: 978-989-8425-89-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
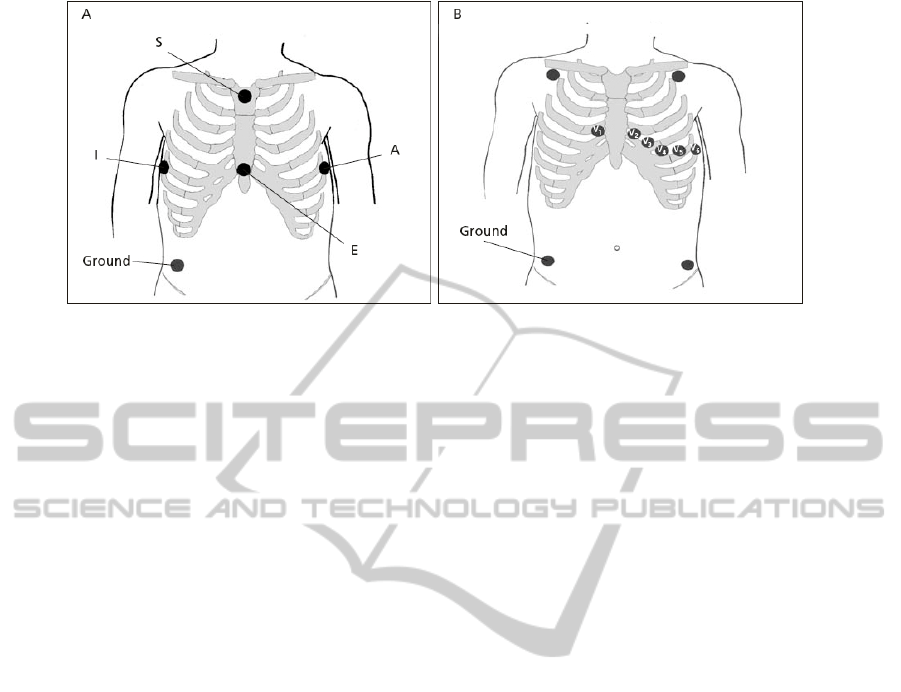
Figure 1: Lead placement for the EASI system (A) and the Mason-Likar (B) 12-lead electrocardiogram.
output variables: I, II, III, aVR, aVL, aVF, V1, V2,
V3, V4, V5, V6 and we used various regression
techniques to build a model.
3 USED METHODS
Four different regression methods were tested to find
a best fitting model, namely Artificial Neural
Network (ANN), Support Vector Regression with
Sequential Minimal Optimization algorithm used,
Linear Regression and Pace Regression.
3.1 Artificial Neural Network
ANN is a system inspired by the operation of
biological neural networks, in other words, is an
emulation of biological neural system. We used
Multilayer Perceptron (MLP) to build the model.
The Multilayer Perceptron method was proven by
the Cybenko theorem to be a universal function
approximator. It uses a backpropagation technique to
train the network. In our experiments MLP used a
sigmoid activation function:
=
1+
(2)
where y
i
is the output of the ith node (neuron) and v
i
is the weighted sum of the input synapses.
Activation function determine whether or not a
neuron fires. The multilayer perceptron consists of
three or more layers (an input and an output layer
with one or more hidden layers) of nonlinearly-
activating nodes. Each node in one layer connects
with a certain weight w
ij
to every node in the
following layer. Learning in the network is done by
changing connection weights after each piece of data
is processed, based on the amount of error in the
output compared to the expected result. To obtain
the best model hundreds of different networks were
built, with different values of learning rate and
various number of hidden layers (nodes).
3.2 Support Vector Regression
The Support Vector algorithm is a nonlinear
generalization of the Generalized Portrait algorithm
developed in Russia in the sixties. As such, it is
firmly grounded in the framework of statistical
learning theory, or VC theory, which has been
developed over the last three decades by Vapnik and
Chervonenkis. Due to this industrial context, SV
research has up to date had a sound orientation
towards real-world applications. Initial work focused
on OCR (optical character recognition). Within a
short period of time, SV classifiers became
competitive with the best available systems for both
OCR and object recognition tasks. We tested three
kernels for SV regression:
- The RBF kernel.
- The polynomial kernel.
- The normalized polynomial kernel.
3.3 Linear Regression
The next regression technique used was a classic
linear regression. In general this technique fits a
linear model to a set of data. Because the model
generated is a linear model this approach is simple
and easy to use, which makes this approach
extensively used in practical applications.
3.4 Pace Regression
Last method used was Pace Regression method.
Pace Regression improves on classical ordinary least
squares (OLS) regression by evaluating the effect of
FINDING NEW EASI ECG COEFFICIENTS - Improving EASI ECG Model using Various Regression Techniques
407
each variable and using a clustering analysis to
improve the statistical basis for estimating their
contribution to overall regression. As well as
outperforming OLS, it also outperform – in a
remarkably general sense – other linear modelling
techniques in the literature, including subset
selection procedures, which seek a reduction in
dimensionality that falls out as a natural byproduct
of pace regression.
4 RESULTS
4.1 Improved Model
Based on results obtained from all tested methods
one linear model was generated:
= 0.2143 × E + 0.1146 × A
−1.0935 × S + 0.7287 × I − 3.0685
(3)
= −0.1298 × + 0.5988 ×
−1.6804 × + 2.3043
(4)
= −0.0845 × − 0.1195 × + 0.4929
× + 0.9408 × + 0.7811
(5)
= −0.0302 × + 0.083 × + 0.0718
× − 1.7402 ×
+ 1.0043
(6)
= 0.1992 × + 0.1561 × − 1.0576
× − 0.1414 × − 2.5664
(7)
= 0.2295 × + 0.0731 × − 1.1295
× + 1.5988 ×
−3.5707
(8)
1 = 0.6344 × + 0.0799 × + 0.501
× + 0.4933 ×
+ 4.0389
(9)
2 = 1.0836 × − 0.095 × + 0.5252
× −1.249 ×
+ 13.6635
(10)
3 = 0.7993 × + 0.2801 × + 0.0881
× − 2.3115 ×
+ 5.0573
(11)
4 = 0.368 × + 1.2349 × + 0.0869
× − 1.1872 × − 2.2414
(12)
5 = 0.1384 × + 1.5578 × + 0.0865
× + 0.3616 × + 0.024
(13)
6 = 0.0362 × + 1.2552 × − 0.1469
× + 0.706 ×
−1.2352
(14)
4.2 Results Comparison
Each model calculation was 10 fold cross validated.
All results are based on data from PhysioNet
database and also on data that were artificially
generated according to the following equations
(described in the paper “Investigation Of A Transfer
Function Between Standard 12-Lead ECG And
EASI ECG”):
E = 6.4073889 × II 4.58091464 × aVR +
4.4236590 × aVF + 1.4023342 × V1 –
0.2316670 × V2 + 0.63803224 × V3
0.3104148 × V4 0.5253245 × V5 + 0.7453142
× V6
(15)
A = 0.1205489 × I + 0.1440902 × aVL
0.07460267 × V1 – 0.005248586 × V2 +
0.04413031 × V3 0.001846735 × V4 +
0.14529887 × V5 + 0.5326776 × V6
(16)
S = 0.9615144 × II + 0.07950829 × aVL +
0.21000511 × aVF – 0.096557012 × V1 +
0.3608502 × V2 0.32692627 × V3 +
0.252434208 × V4 + 0.04650518 × V5
0.1318653 × V6
(17)
I = 0.1494002 × I 0.24593780 × aVL
0.003465868 × V1 – 0.1516211491 × V2 +
0.2637671 × V3 0.17090946 × V4 +
0.03756737 × V5 0.10936146 × V6
(18)
Calculated models were compared with results
obtained using classical Dower approach and also
with Improved EASI Coefficients described in the
paper “Improved EASI Coefficients: Their
Derivation, Values, and Performance” by Dirk Q.
Feild, Charles L. Feldman, and B. Milan Horacek.
To determine performance of all systems, for each of
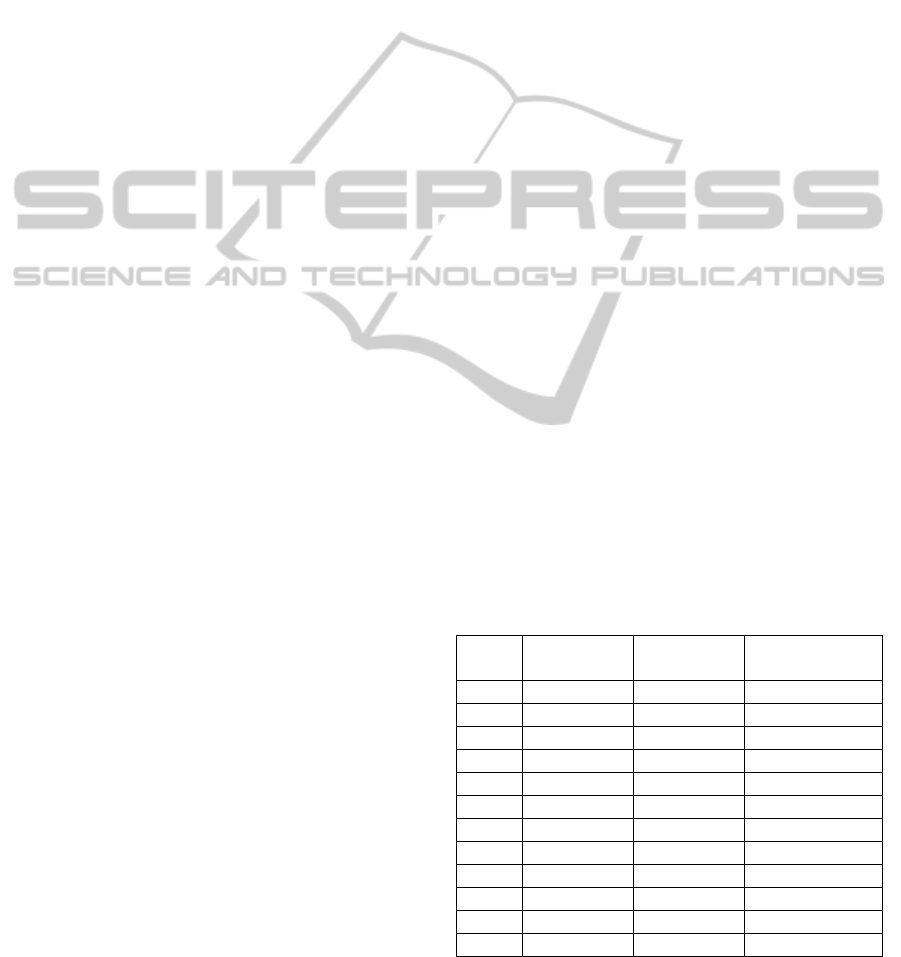
them correlation coefficient (Table 1) and root mean
squared error (Table 2).
4.3 Tables
Table 1: Correlation coefficients comparison.
Obtained
Model
EASI Dower
approach
Improved EASI
Coefficients
aVF 0,939 0,984 0,776
aVL 0,966 0,955 0,922
aVR 0,984 0,985 0,966
I 0,985 0,971 0,973
II 0,964 0,994 0,894
III 0,941 0,963 0,786
V1 0,99 0,882 0,849
V2 0,984 0,968 0,872
V3 0,975 0,971 0,751
V4 0,971 0,981 0,851
V5 0,992 0,977 0,97
V6 0,997 0,888 0,985
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
408

Table 2: Root Mean Squared Error comparison.
Obtained
Model
EASI Dower
approach
Improved EASI
Coefficients
aVF 27,45 28,41 66,29
aVL 22,02 35,45 34,22
aVR 16,03 31,86 55,3
I 18,01 40,75 42,47
II 26,13 32,57 78,2
III 31,41 37,19 60,03
V1 21,01 99,24 86,42
V2 40,54 177,75 119,61
V3 46,62 120,25 141,69
V4 55,6 144,6 129,96
V5 24,66 119,93 49,9
V6 10,77 93,17 33,1
5 CONCLUSIONS
Above results show that the best performance was
obtained for the linear model built using regression
techniques. Second best model was one created by
Dower. Surprisingly low performance was observed
for model that uses improved EASI coefficients.
Further work in the topic of improving EASI
ECG coefficient using various regression techniques
should be continued.
ACKNOWLEDGEMENTS
This work was supported by the European
Community from the European Social Fund.
REFERENCES
Dower G. E., Yakush A., Nazzal S. B., Jutzy R. E., Ruiz
C. E., Deriving the 12-lead electrocardiogram from
four (EASI) electrodes. J Electrocardiol.
1988;21(suppl):S182-S187.
C. L. Feldman, G. MacCallum, L. H. Hartley. Comparison
of the Standard ECG with the EASIcardiogram for
Ischemia Detection During Exercise Monitoring J
Facts 1991;21:201-9.
Klein M. D., Key-Brothers I., Feldman C. L., Can the
vectorcardiographically derived EASI ECG be a
suitable surrogate for the standard ECG in selected
circumstances? In: Computers in Cardiology.
Piscataway, NJ: IEEE Computer Society Press;
1997:721-724.
Darawan Chantad, Rungroj Krittayaphong, Chulalak
Komoltri. Derived 12-lead electrocardiogram in the
assessment of ST-segment deviation and cardiac
rhythm. Journal of Electrocardiology 39 (2006) 7 – 12.
Barbara J., Drew, Michele M., Pelter, Shu-Fen Wung,
Mary G., Adams, Carrie Taylor, G., Thomas Evans
and Elyse Foster. Accuracy of the EASI 12-Lead
Electrocardiogram Compared to the Standard 12-
Lead Electrocardiogram for Diagnosing Multiple
Cardiac Abnormalities. Journal of Electrocardiology
Vol. 32 Supplement 1999.
Welinder A., Sfrnmo L., Feild D. Q., et al., Comparison of
signal quality between EASI and standard Mason-
Likar 12-lead electrocardiograms during physical
activity. Am J Crit Care 2004;13:228. 4.
Dower G. E., EASI 12-Lead Electrocardiography.
Totemite Publishers, Point Roberts, WA, 1996
G. Cybenko. Approximations by superpositions of
sigmoidal functions. Mathematics of Control, Signals,
and Systems, 2:303-314, no. 4 pp. 303-314.
Alex J., Smola, Bernhard Scholkopf. A Tutorial on
Support Vector Regression.
Wang, Y. and Witten, I. H. (1999). Pace Regression.
(Working paper 99/12). Hamilton, New Zealand:
University of Waikato, Department of Computer
Science.
Dirk Q., Feild, Charles L. Feldman and B. Milan Horacek,
Improved EASI Coefficients: Their Derivation, Values,
and Performance, Journal of Electrocardiology Vol.
35 Supplement 2002.
Wojciech Oleksy, Ewaryst Tkacz, Investigation Of A
Transfer Function Between Standard 12-Lead
ECG And EASI ECG, 20th International Eurasip
Conference Biosignal 2010
http://www.physionet.org/challenge/2007/data/
FINDING NEW EASI ECG COEFFICIENTS - Improving EASI ECG Model using Various Regression Techniques
409
