DECOMPOSITION OF MULTIMODAL DATA FOR

AFFORDANCE-BASED IDENTIFICATION OF POTENTIAL GRASPS

Daniel Dornbusch

, Robert Haschke

, Stefan Menzel

and Heiko Wersing

CoR-Lab, Bielefeld University, Bielefeld, Germany

Honda Research Institute Europe GmbH, Offenbach, Germany

Keywords:

Decomposition algorithms, Multimodal data, Grasp identiﬁcation.

Abstract:

In this paper, we apply standard decomposition approaches to the problem of ﬁnding local correlations in

multi-modal and high-dimensional grasping data, particularly to correlate the local shape of cup-like objects

to their associated local grasp conﬁgurations. We compare the capability of several decomposition methods to

establish these task-relevant, inter-modal correlations and indicate how they can be exploited to ﬁnd potential

contact points and hand postures for novel, though similar, objects.

1 INTRODUCTION

We tackle the challenging problem of ﬁnding suitable

grasps for unknown objects employing well-known

decomposition approaches. In order to grasp an un-

known object, previously acquired grasping knowl-

edge from similar objects needs to be exploited and

adapted to the current situation. Because similar ob-

ject shapes, e.g. handles, also afford similar hand pos-

tures for grasping, we are looking for correlations be-

tween different modalities of successful grasping ex-

amples. Based on depth images and object silhouettes

extracted from color images, we aim for a prediction

of contact locations as well as an associated hand pos-

ture to realize the grasp. In doing so, we especially

focus on local shape features, because different local

parts of an object afford different grasps.

Unsupervised decomposition algorithms are able

to ﬁnd statistically relevant correlations in high-

dimensional data sets, and thus are well-suited to the

task at hand. Applying them to a multimodal data set

allows for the identiﬁcation of inter-modal, semanti-

cally meaningful correlations. The simultaneous use

of multimodal data in decomposition approaches can:

(i) improve the interpretability of the extracted ba-

sis components of each single modality, and (ii) ex-

tract functionally relevant correlations between dif-

ferent modalities. In Sec. 3, several decomposition

methods, brieﬂy introduced in the next section, are

compared w.r.t. their ability to establish relevant inter-

modal correlations in training data, and to infer grasps

for new, though similar, objects. Finally, in Sec. 4 we

discuss the results and draw some conclusions.

2 MATRIX DECOMPOSITION

The starting point of all decomposition approaches is

a set of L vectors x

∈ R

pooled in an input matrix

X = [x

, . . . , x

]. Each x

can be regarded as an ob-

servation of M random variables, comprising several

modalities. We aim for a more compact, approximate

representation of these observations using a small set

of N <ML meaningful components spanning a new

vector space F = [f

, . . . , f

]. This assumes that ob-

servations lie on a low-dimensional manifold of R

which here is approximated by a linear subspace. The

basis vectors f

will express typical correlations within

the training set, also including correlations between

different modalities of the data. Expressing the data

vectors x

with respect to the basis F yields an approx-

imation matrix, R = [r

, . . . , r

]. The N ×L matrix G

of coefﬁcients is known as the encoding matrix.

Formally, we can restate this approach as matrix

factorization, X ≈ F ·G ≡ R, which minimizes the re-

construction error between the original data, X, and

its factorization, F · G. The computation of F and G

depends on the actual decomposition approach, which

may impose additional constraints on both matrices,

e.g., sparseness or non-negativity.

For example, PCA (Zhao et al., 2008) computes

basis vectors that are pairwise orthogonal and point in

the directions of the largest variances. k-Means clus-

tering (Li and Ding, 2006) represents observations by

585

Dornbusch D., Haschke R., Menzel S. and Wersing H. (2012).

DECOMPOSITION OF MULTIMODAL DATA FOR AFFORDANCE-BASED IDENTIFICATION OF POTENTIAL GRASPS.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 585-589

DOI: 10.5220/0003790205850589

 SciTePress

a set of prototypes, f

, resulting in an extremely sparse

encoding: only the coefﬁcient associated to the near-

est prototype equals one. Non-negative Matrix Fac-

torization (NMF) (Zhao et al., 2008) constrains basis

vectors and encodings to non-negative values to avoid

cancellations of features and facilitates their inter-

pretability. Non-negative Matrix Factorization with

Sparseness Constraints (NMF-SC) (Hoyer, 2004) is

based on NMF and additionally enforces sparseness

on the encodings and/or the basis components.

3 APPLICATION TO GRASPING

We compare the presented decomposition approaches

in a grasping scenario to investigate their ability to

ﬁnd local inter-modal correlations. Based on a dataset

of successful grasps applied to a set of cups, a com-

pact set of basis components is calculated. In a sub-

sequent application step, partial observations are aug-

mented by a reconstruction of the missing modalities.

To this end, encodings are computed based on exist-

ing modalities and missing ones are predicted from

the corresponding linear combination of basis com-

ponents. Finally, the best grasp can be chosen and

realized by a robot hand.

3.1 Capturing of Grasping Data

To gather multimodal information of human grasping

processes, the Manual Interaction Lab was created at

CITEC, Bielefeld (Maycock et al., 2010). For the

work presented in this paper, data from three modal-

ities were captured: hand postures (motion-tracking

coordinates), color video images and depth images.

16 different cup-like objects were selected to record

grasping sequences belonging to three different grasp

types: cup grasped by handle, from above, or from the

side. 413 grasp conﬁgurations were captured, com-

prising 8-9 grasps per object and grasp type.

3.2 Preprocessing of Grasping Data

The captured raw sensor data was synchronized and

preprocessed to obtain suitable input data for the

grasp selection task.

Visual Modalities. The grasp for a particular ob-

ject is ﬁrst and foremost determined by the shape of

the object. A preliminary study using color images

for decomposition resulted in basis components dom-

inated by colors and textures. Hence, we decided to

extract the object silhouette from these images, i.e.

those pixels constituting the object shape. We also re-

moved constant background pixels from all color and

Figure 1: Modalities: (a) Color video image. (b) Object

silhouette and contact areas. (c) Swiss Ranger depth image.

(d) Visualization of Vicon coordinates. (e) Grasp type.

depth images, replacing them with zero values. Thus,

the decomposition approaches do not need to explic-

itly model these irrelevant image parts. Contact re-

gions on the object silhouette were identiﬁed by com-

paring images before and after establishing the grasp.

All depth and color images were centered, cropped

to the foreground region, and resized for normaliza-

tion purposes. The image sizes of the sparse input

modalities were 144 × 100 for the object silhouettes

and contact regions and 61 × 46 for the depth images.

Hand Posture. Hand posture sequences, obtained

from tracking markers on all ﬁnger segments and sub-

sequent calculation of the associated hand posture

(Maycock et al., 2011), can be utilized in two man-

ners: using the whole grasping trajectory or the ﬁ-

nal grasp posture only. In preliminary studies, we

found that complete trajectories can be reconstructed

in many cases. However, different grasping speeds

and large variations of hand trajectories prior to ac-

tual grasping sometimes lead to visible dilatation ef-

fects in the reconstructed trajectories. Dynamic Time

Warping (M

uhlig et al., 2009) could compensate for

asynchronous execution speeds and might in future

work allow direct “replay” on a robot hand. In this

paper, only the ﬁnal hand pose is considered, adding

a 27 × 3 dimensional vector of marker positions to the

input data.

Grasp Type. To distinguish the three employed

grasp types, we could learn three individual sets of

basis components, F

, employing appropriate subsets

of the training data. However, this strongly reduces

the number of data samples available for decomposi-

tion. Alternatively, a single decomposition could be

applied to the entire training set comprising all grasp

types, which often leads to an interference of basis

components corresponding to different grasp types.

In order to choose a particular grasp type, we aug-

mented all input vectors by an additional modality,

employing three-dimensional unit vectors to indicate

the grasp type. Then, we can explicitly request a par-

ticular grasp type by providing the corresponding unit

vector as an additional input to the search process.

This prevents simultaneous activation of basis com-

ponents belonging to different grasp types, thus re-

ducing co-activation of ambiguous local grasps. Fur-

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

586

(a) (b) (c) (d)

Figure 2: 4 of 250 exemplary basis components calculated

by NMF-SC. Top: overlap of object silhouettes (green) and

contact areas (red), middle: depth image, bottom: grasp

type. Grasp posture not visualized. (a) Cup corpus. (b)

Grasp by handle. (c) Grasp from above. (d) Grasp from side.

thermore, grasp-speciﬁc correlations between modal-

ities are automatically labeled by the decomposition

algorithms. Finally, the combined decomposition of

all grasp conﬁgurations has the advantage that corre-

lations, which are common to different grasp types,

have to be learned just once.

All employed input modalities are summarized in

Figure 1 along with the original color image, which

is not included in the input data. Altogether, the data

vectors comprise 14400 + 14400 + 2806 + 81 + 3 =

31690 dimensions.

3.3 Calculation of Basis Components

In the ﬁrst study, we applied the decomposition algo-

rithms to a training data set consisting of 320 grasp

conﬁgurations, derived from 13 of the 16 cup-like ob-

jects. We extracted subspaces spanned by 50, 100,

150, 200, 250 and 320 basis components. Addition-

ally, we used a disjoint test data set comprising 93

grasp conﬁgurations belonging to the three remain-

ing cups to measure the ability of the methods to

generalize and represent novel, though similar, data.

In this study, the encodings used for reconstruction

were computed based on all modalities (depth images,

hand postures, object silhouettes, contact areas and

labeled grasp types). k-Means clustering produced

prototypical, holistic and non-negative basis vectors.

The encodings were maximally sparse and the abil-

ity to generalize was limited to the selection of the

nearest cluster centroid. The principal components of

PCA accomplished very small reconstruction errors,

but were difﬁcult to interpret due to their holistic na-

ture and the occurrence of positive and negative val-

ues. The non-negative basis components produced by

NMF were mostly sparse. The encoding matrix was

always sparse and non-negative. NMF-SC computed

only sparse, non-negative basis components and en-

codings such as the sparseness constraint was explic-

itly enforced by the algorithm. Figure 2 depicts four

Table 1: Study 1 – Normalized mean squared reconstruction

errors (NMSE) for observed (a) and test data set (b) against

number of basis components. The encodings used for re-

construction are computed based on all modalities (depth

images, grasp postures, object silhouettes, contact areas and

labeled grasp types). Values scaled up by a factor of 10

Approach (a) Training Data

50 100 150 200 250 320

K-Means 75.7 49.4 31.7 18.3 10.8 0.0

PCA 39.1 20.4 11.7 6.4 2.8 0.0

NMF 52.1 31.1 20.2 12.1 7.8 2.5

NMF-SC 55.9 32.5 20.4 11.5 7.1 1.8

(b) Test Data

K-Means 163.2 167.6 165.5 176.0 174.1 179.0

PCA 91.7 80.3 74.2 70.8 68.0 65.6

NMF 107.1 97.8 94.7 95.1 94.9 98.2

NMF-SC 111.0 104.3 102.3 102.2 99.1 102.4

exemplary basis vectors, which represent local fea-

tures like the cup handle or the body. As Table 1

shows, the normalized mean squared reconstruction

error

NMSE =

∑

i=1

− r

, (1)

calculated on the training data decreases for all meth-

ods uniformly, as the number of available basis com-

ponents is increased from 50 to 320. Using the maxi-

mal number of basis components, k-Means clustering

and PCA are able to represent the training data per-

fectly. In contrast to this, for the test data set the

inverse correlation between NMSE and the feature

count did not always hold true. In particular, k-Means

did not beneﬁt from higher numbers of basis compo-

nents. Also, NMSE increased again using the full set

of basis vectors generated by NMF and NMF-SC due

to overspecialization. Only PCA proﬁted in all cases

as additional basis component were added.

3.4 Identiﬁcation of Potential Grasps

for Novel Cup-like Objects

In the second study, we reconstructed missing modali-

ties based on the inherent correlations between the ba-

sis components’ subparts leading to the generation of

potential grasp conﬁgurations for novel, though sim-

ilar, objects. We calculated the encodings for the test

observations based only on the following modalities:

depth images (measured), object silhouettes (com-

puted from color video images) and desired grasp

types (set manually). In a second step, we utilized

these encodings to reconstruct all modalities, includ-

ing the previously neglected contact areas and grasp

postures. Since the basis vectors were specialized to

represent the correlations in grasping data, the miss-

DECOMPOSITION OF MULTIMODAL DATA FOR AFFORDANCE-BASED IDENTIFICATION OF POTENTIAL

GRASPS

587

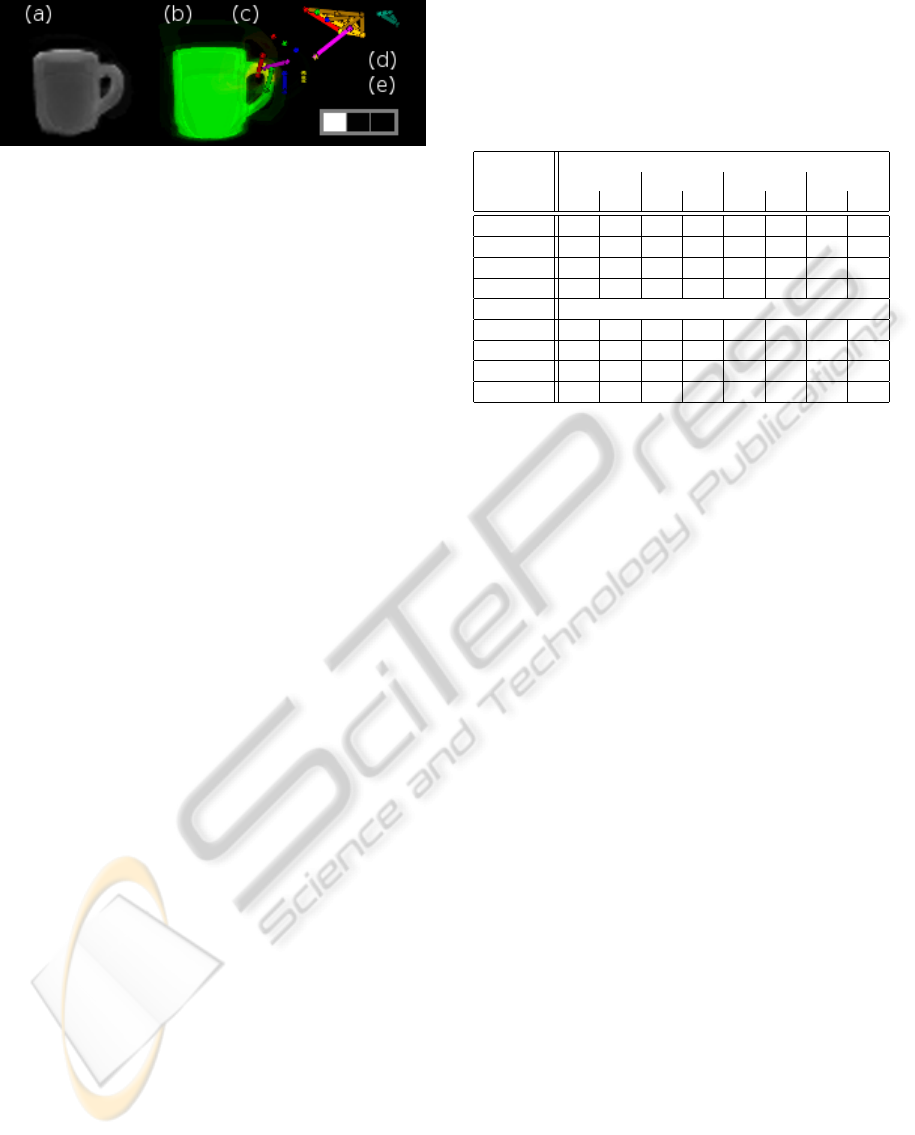
Figure 3: Potential grasp identiﬁed by NMF-SC for a new

test cup, which was not used for training: Reconstructed

depth image (a), contact area (c) and grasp posture (d) on

top of the object silhouette (b), desired grasp type (e).

ing information was approximated successfully for

most novel objects (see Figure 3). Acknowledging

the problem of overspecialization detected in the ﬁrst

study, we decided to investigate only the 150 (best

error per component ratio) and 250 basis compo-

nent (best before overspecialization) cases. To ana-

lyze the reconstruction errors for the approximation of

the missing modalities, we calculated the normalized

mean squared reconstruction errors (NMSE) com-

bined for all modalities (see Table 2a) and the com-

bined NMSE only for the measured modalities (see

Table 2b). Additionally, we evaluated the reconstruc-

tions of the formerly missing contact areas and grasp

postures to assess the quality of the identiﬁed poten-

tial grasp conﬁgurations. This was done by calculat-

ing the mean contact region error E

(see Table 2c),

which is the average distance of the estimated and the

expected contact area centroids (averaged over all L

observations). Furthermore, we computed the mean

ﬁngertip error E

(see Table 2d), which is the average

error of the estimated and the expected ﬁngertip po-

sitions. We found that the performance of k-Means

on the test data set derogated using 250 feature vec-

tors compared to 150, but still inferred the best over-

all grasp conﬁgurations for novel objects. PCA also

produced good reconstruction errors, but sometimes

resulted in diffuse contact areas for test objects due

to its holistic basis features. NMF did not have this

problem, because of its mostly sparse basis compo-

nents. NMF-SC performed good at representing the

measured modalities and the contact areas. However,

the reconstruction error of generated grasp postures is

larger. In summary, all algorithms were able to pre-

dict realistic grasp conﬁgurations in most cases.

3.5 Selection of Best Grasp

To select the best suited grasp for a novel object, a

method has to be found in future work that is able to

sort potential grasps by their quality, e.g., by evaluat-

ing the reconstruction errors of the measured modali-

ties, or the sparseness of the inferred contact areas.

Table 2: Study 2 – modality reconstruction: Encodings are

computed based only on measured modalities and used to

reconstruct missing modalities, i.e. contact areas and grasp

postures. NMSE of (a) all and (b) measured modalities.

NMSE scaled up by a factor of 10

. E

: Mean distance of

estimated and expected contact area centroids (c). E

: Mean

error of estimated and expected ﬁngertip positions (d).

Training Data

Approach (a) AM (b) MM (c) E

(d) E

150 250 150 250 150 250 150 250

K-Means 37.3 13.2 63.4 23.4 1.79 0.76 6.2 2.5

PCA 25.2 5.5 61.5 13.8 1.13 0.21 8.1 3.2

NMF 35.4 11.4 78.2 23.7 2.64 0.76 9.1 3.9

NMF-SC 25.7 8.8 48.2 17.0 1.50 0.56 13.6 4.7

Test Data

K-Means 195 228 293 354 5.3 5.8 21.8 23.1

PCA 162 158 340 337 8.7 7.8 27.3 25.5

NMF 207 161 455 309 13.2 10.2 31.6 25.9

NMF-SC 151 139 258 233 5.5 5.3 52.0 33.2

4 CONCLUSIONS

The decomposition approach provides a method to

predict missing modalities from a few measurable

modalities as long as strong correlations exist be-

tween both groups. We have shown that this approach

can be used to predict hand conﬁgurations and de-

sired contact regions for grasping an object based on

its depth image and silhouette. This grasp information

can subsequently be utilized for autonomous grasping

– either by directly actuating a robot hand towards the

estimated hand posture, or by computation of a hand

posture realizing the estimated contact locations on

the object. In both cases, an inverse hand kinematic

can be used to obtain joint angles to actually operate

the robot hand (Maycock et al., 2011).

ACKNOWLEDGEMENTS

Daniel Dornbusch gratefully acknowledges the ﬁnan-

cial support from Honda Research Institute Europe.

REFERENCES

Hoyer, P. O. (2004). Non-negative matrix factorization with

sparseness constraints. JMLR, 5:1457–1469.

Li, T. and Ding, C. (2006). The relationships among various

nonnegative matrix factorization methods for cluster-

ing. In Proc. ICDM, Washington.

Maycock, J., Dornbusch, D., Elbrechter, C., Haschke, R.,

Schack, T., and Ritter, H. J. (2010). Approaching

manual intelligence. KI - K

unstliche Intelligenz, 24.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

588

Maycock, J., Steffen, J., Haschke, R., and Ritter, H. (2011).

Robust tracking of human hand postures for robot

teaching. In Proc. IROS, San Francisco.

uhlig, M., Gienger, M., Hellbach, S., and Goerick, C.

(2009). Task-level imitation learning using variance-

based movement optimization. In Proc. ICRA. IEEE.

Zhao, L., Zhuang, G., and Xu, X. (2008). Facial expres-

sion recognition based on PCA and NMF. In Proc.

WCICA, Chongqing, China.

DECOMPOSITION OF MULTIMODAL DATA FOR AFFORDANCE-BASED IDENTIFICATION OF POTENTIAL

GRASPS

589