
PARAMETER AND CONFIGURATION ANALYSIS FOR
NON-LINEAR POSE ESTIMATION WITH POINTS AND LINES
Bernhard Reinert, Martin Schumann and Stefan Mueller
Institute of Computational Visualistics, University of Koblenz, Koblenz, Germany
Keywords:
Camera Pose Tracking, Model Features, Correspondences, Non-linear Optimization.
Abstract:
In markerless model-based tracking approaches image features as points or straight lines are used to estimate
the pose. We introduce an analysis of parametrizations of the pose data as well as of error measurements
between 2D image features and 3D model data. Further, we give a review of critical geometrical configurations
as they can appear on the input data. From these results the best parameter choice for a non-linear pose
estimator is proposed that is optimal by construction to handle a combined input of feature correspondences
and works on an arbitrary number and choice of feature type. It uses the knowledge of the 3D model to analyze
the input data for critical geometrical configurations.
1 INTRODUCTION
Model-based camera pose tracking is the process of
estimating the viewing position and orientation of a
camera by establishing 2D-3D correspondences be-
tween features of the model and the camera image.
Estimating the pose can be done by using linear or
non-linear solutions. Most pose algorithms origi-
nate from the domain of linear solutions and oper-
ate on point or line features. Combining both fea-
ture types has been done, but no complete comparison
of parametrization and error measurements for non-
linear solutions is available. Further, a priori model
knowledge should be used to improve stability of a
combined solution.
We provide a discussion on possible parametriza-
tions of the camera pose, including its constraints
which must be taken into account during or after the
optimization process as well as on several error mea-
surements for the feature correspondences to be min-
imized by the optimization process. Further, we give
a review of critical configurations as they are known
to cause ambiguous results on the input geometry of
points and lines. From these results we propose the
best parameter choice for a non-linear pose estima-
tor that is optimal by construction for the acceptance
of point and line correspondences in arbitrary com-
bination and number. The estimator takes account
of critical configurations of the input data by using
the knowledge of the 3D model and selecting the best
miminal correspondence set for a stable solution. We
investigate the behaviour on variable input types and
numbers of correspondences, as well as the influence
of noise on the robustness of the pose.
2 RELATED WORK
The problem of camera pose estimation with 2D-
3D correspondences of points is known as the
perspective-n-point problem (PnP) (Fischler and
Bolles, 1981). There are several approaches to the so-
lution of P3P surveyed and compared for their numer-
ical stability by (Haralick et al., 1994). While these
linear solutions work on a fixed number of three point
correspondences, (Lepetit et al., 2009) introduce vir-
tual control points to make possible a solution for ar-
bitrary numbers of point correspondences (PnP) with
linear complexity. Another linear solution for any
number of point or line correspondences is given by
(Ansar and Daniilidis, 2003) but does not work on
both types of features simultaneously.
Most of the non-linear solutions are based
on classical iterative algorithms of optimization,
like the Gauss-Newton- or Levenberg-Marquardt-
Method. Non-linear pose with line correspondences
has been estimated by (Kumar and Hanson, 1994)
who analyzed the influence of certain line represen-
tations on the optimization process. A solution using
arbitrary line traits on an object is shown by (Lowe,
1991). Possible error measurements for point corre-
271
Schumann M., Reinert B. and Mueller S..
PARAMETER AND CONFIGURATION ANALYSIS FOR NON-LINEAR POSE ESTIMATION WITH POINTS AND LINES.
DOI: 10.5220/0003827402710276
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 271-276
ISBN: 978-989-8565-04-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

spondences were analyzed by (Lu et al., 2000), who
also proposed a new possibility requiring fewer itera-
tions. In (Dornaika and Garcia, 1999) points and lines
are combined under an extension of the well-known
POSIT algorithm with additional optimization.
Joint usage of point and line correspondences ex-
ists in the field of linear solutions and to a lesser extent
in non-linear approches. But most authors analyze
one parametrization and a single error measurement
only, when solving for the camera pose. So in sec-
tions 4, 5 and 7 we will first give a full analysis of
error measurements and parametrizations to find the
best fitted parameters for constructing combined non-
linear pose. An overview of critical configurations for
points is given by (Fischler and Bolles, 1981), where
(Wolfe et al., 1991) prove the number of solutions for
P3P geometrically as (Hu and Wu, 2002) and (Gao
and Tang, 2006) do for P4P. An example for critical
line configurations is given by (Christy and Horaud,
1999). We will address the problem of recognizing
such configurations in section 9.
3 DEFINITIONS
The pose problem can be described as the estima-
tion of the extrinsic camera parameters relative to a
known reference coordinate system, i.e. the world
coordinate system, from given correspondences be-
tween 2D features ~q of a camera image and 3D fea-
tures ~p of a synthetic model. The coordinate system
of a value is identified by a superscript w for world-, c
for camera-, i for image- and p for pixel-coordinate-
system. For all coordinate systems, the normalized
vector of ~p is denoted by
~
ˆp. The camera pose is rep-
resented in combination as a tuple consisting of a rota-
tion matrix R ∈ R
3x3
and a translation vector
~
t ∈ R
3
as
C :
R,
~
t
and represents the transformation of a point
~p between world- and camera-coordinate-system as
~
p
c
= R
~
p
w
+
~
t. The intrinsic camera matrix K is as-
sumed to be known by calibration. Hence, given a
world point
~
p
w
and K, its pixel coordinates
~
p
p
can be
calculated by perspective projection. A point corre-
spondence between the world point
~
p
w
and the pixel
point
~
q
p
is represented by a tuple k
p
:
~
p
w
,
~
q
p
.
The line features in the camera images are defined
as straight lines l : (φ
p
,ρ
p
) with infinite extent. φ
p
represents the angle between the line normal and the
y-axis of the pixel coordinate system and ρ
p
is the
orthogonal distance of the line from the image origin.
Hence, for each point
~
p
p
∈ l it holds
cosφ
p
p
p
x
+ sinφ
p
p
p
y
= ρ
p
. (1)
A straight line correspondence is represented by two
world points
~
s
w
and
~
e
w
(typically start- and endpoint)
of the model line and an image line l
p
: (φ
p
,ρ
p
) by a
tuple k
l
:
(
~
s
w
,
~
e
w
),l
.
4 ERROR MEASUREMENTS FOR
POINTS
Since the aim is to minimize the distance between
the transformed model feature and camera image fea-
ture, error measurements, i.e. residuals, for corre-
spondences have to be defined. We investigated three
different point residuals which measure the error in
different coordinate-systems (Figure 1).
The well-known Reprojection-Error measures
the distance between the image feature
~
q
p
and the
model feature
~
p
p
after its projection to the image
plane in pixel-coordinates. Hence, the residual for
each correspondence k
p
becomes
~r
RE
=
~
p
p
−
~
q
p
=
p
p
x
− q
p
x
p
p
y
− q
p
y
. (2)
The Object-Space-Error measures the distance
in camera-coordinates and was introduced by (Lu
et al., 2000). To recover the depth for the image fea-
ture, its normalized sight vector
~
ˆ
q
c
(i.e. the connect-
ing vector from the camera center to the feature) is
projected onto the sight vector of the model
~
p
c
. The
resulting scalar is used to scale the normalized sight
vector of the image
~
ˆ
q
c
and both sight vectors are then
compared based on their camera coordinates. The
residual per correspondence k
p
becomes
~r
OE
=
p
c
x
−
D
~
ˆ
q
c
,
~
p
c
E
ˆ
q
c
x
p
c
y
−
D
~
ˆ
q
c
,
~
p
c
E
ˆ
q
c
y
. (3)
It has to be noted that points whose projections on the
image plane are the same produce greater residuals
for greater distances from the image plane, i.e. are
not depth invariant.
The Normal-Space-Error also measures the dis-
tance in the camera-coordinates. From the image fea-
ture
~
q
c
two orthogonal normals
~
n
c
1
and
~
n
c
2
can be cre-
ated, describing the direction of the sight vector of the
image in camera-coordinates. The dot product of the
normalized normals and the sight vector of the model
~
p
c
provides a measurement between image and model
features and the residual per correspondence k
p
be-
comes
~r
NE
=
D
~
ˆ
n
c
1
,
~
p
c
E
D
~
ˆ
n
c
2
,
~
p
c
E
. (4)
The Normal-Space-Error is not depth invariant as
well.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
272
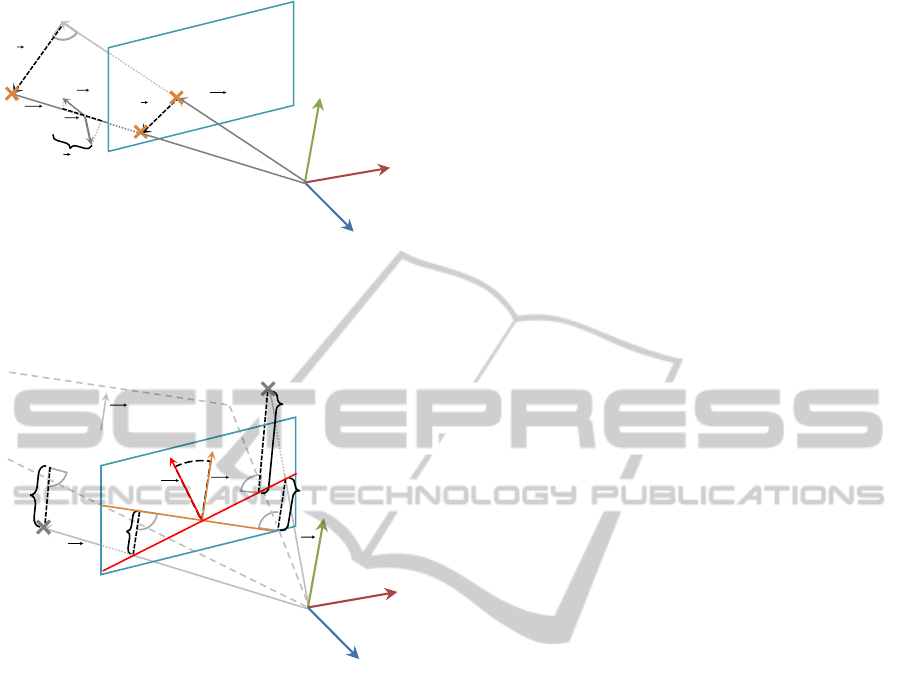
×
c
q
c
p
1
n
RE
r
OE
r
NE
r
2
n
I
c
Figure 1: Error measurements for points. Shown are the
camera coordinate system c, the image plane I, the vectors
for model and image feature
~
p
c
and
~
q
c
, the normals of the
Normal-Space-Error ~n
1
and ~n
2
together with their projec-
tion on
~
p
c
and the error measurements~r
RE
,~r
OE
and~r
NE
.
×
×
×
×
PE
s
r
PE
e
r
AELE
e
rr
r
,
LE
s
r
AE
r
j
p
l
p
l
c
s
c
e
c
E
p
l
n
p
n
l
c
E
n
I
c
Figure 2: Error measurements for lines. Shown are the
camera coordinate system c, the image plane I, the model
and image feature
~
s
c
,
~
e
c
and l
p
, the line ℓ
p
, their normals
~
n
p
l
and
~
n
p
ℓ
, the plane E
c
with its normal
~
n
c
E
and the components
of the error measurements~r
AE
,~r
LE
and~r
PE
.
5 ERROR MEASUREMENTS FOR
LINES
We investigated three different line residuals which
measure the error in different coordinate-systems
(Figure 2).
The Angle-/Distance-Error measures the differ-
ences of the angles and the distances of the image and
model feature. The start- and endpoint of the model
feature are transformed into their pixel points
~
s
p
,
~
e
p
to compute the conjunctive line ℓ : (ϕ
p
,d
p
), which is
compared to the image line l
p
. The residual per cor-
respondence k
l
therefore becomes
~r
AE
=
ϕ
p
− φ
p
d
p
− ρ
p
. (5)
Noteable for this error measurement is that the dimen-
sions of the angle and the distance are not equal.
The Line-Error measures the distances of the
projected start- and endpoint
~
s
p
,
~
e
p
to the image line
l
p
and is used, among others, by Lowe (Lowe, 1991).
Hence, from Eq. 1 the residual for each correspon-
dence k
l
becomes
~r
LE
=
cosφ
p
s
p
x
+ sinφ
p
s
p
y
− ρ
p
cosφ
p
e
p
x
+ sinφ
p
e
p
y
− ρ
p
. (6)
The Plane-Error can be regarded as the Object-
Space-Error extension for straight lines, i.e. the depth
recovery of the image feature, and is used e.g. by
(Kumar and Hanson, 1994). The optical center and
the image line in camera coordinates l
c
define a plane
E
c
with normal
~
n
c
E
=
cosφ
i
sinφ
i
−ρ
i
T
. For
start- and endpoint in camera coordinates
~
s
c
,
~
e
c
the
distance to this plane can be computed. The residual
for each correspondence k
l
becomes:
~r
PE
=
D
~
ˆ
n
c
E
,
~
s
c
E
D
~
ˆ
n
c
E
,
~
e
c
E
. (7)
Similar to the Object-Space-Error, the Plane-Error is
not depth invariant.
6 OPTIMIZATION
The residuals of all correspondences are joined in one
combined residual~r. The pose parameters for transla-
tion
~
a
t
and rotation
~
a
R
are combined in the parameter
vector~a. The objective is to minimize the sum of the
squared entries of this combined residual in terms of
the pose parameters~a.
argmin
~a
2m
∑
j=0
r
2
j
(8)
To solve this problem standard optimization tech-
niques are used so that the parameter vector is turned
into a sequence h~a
i
i. Since the Gauss-Newton op-
timization is comparatively fast but does not guar-
antee convergence and Gradient-Descent optimiza-
tion is slow but guarantees convergence, we used the
Levenberg-Marquardt optimization that is commonly
known as a technique which guarantees convergence
but is still comparatively fast. The iteration rule is
~a
i+1
= ~a
i
+
~
δ with
~
δ =
J
~r
(~a
i
)
T
J
~r
(~a
i
) + λD
−1
J
~r
(~a
i
)~r(~a
i
), (9)
D = diag
J
~r
(~a
i
)
T
J
~r
(~a
i
)
and J
~r
the Jacobian matrix
of~r. We found the initial value of λ = 10
−3
and an
alteration rule of λ
i
= λ
i−1
/10 for a residual decrease
and λ
i
= λ
i−1
∗ 10
w
with w ∈ N for a residual increase
of the last step to work best.
PARAMETER AND CONFIGURATION ANALYSIS FOR NON-LINEAR POSE ESTIMATION WITH POINTS AND
LINES
273

7 PARAMETRIZATION
We also investigated the influence and conditions
of different parametrizations of the pose. Different
parametrizations of the translation vector
~
t
c
do not
hold any major differences and it is therefore repre-
sented by three scalars t
c
x
, t
c
y
and t
c
z
, describing the
translation in camera coordinates; the translation pa-
rameter vector is
~
a
t
=
~
t
c
.
For rotation parametrization we investigated four
different alternatives. All rotations are described by
their corresponding transformation matrices R and
have to fulfill certain rotation properties since R ∈
SO(R, 3), i.e. the special orthogonal group proper-
ties (SOP). In general, these properties can be assured
at various stages of the optimization process:
I. prior to optimization
By choosing an appropriate rotation parametriza-
tion the SOP can be assured partly or completely
prior to the optimization process.
II. during optimzation
By adding the SOP as additional elements to the
residual vector, these properties are optimized
with the other residuals. A drawback of this al-
ternative is that with the presence of imperfect or
false correspondences the properties are not en-
forced but only minimized according to the least
squares approach of the optimization.
III. after optimization
By employing the singular value decomposition,
a rotation matrix
˜
R can be computed from the es-
timated transformation matrix R that assures the
SOP and is similar to R.
These three possibilities are not exclusionary; alter-
native II. has to be combined with alternative III. for
the SOP to be fulfilled.
The parameter vector of the
Matrix-Parametrization is
~
a
R
=
i
x
i
y
i
z
j
x
j
y
j
z
k
x
k
y
k
z
T
. The
transformation matrix is composed of three vectors
~
i,
~
j,
~
k ∈ R
3
:
R
M
=
i
x
i
y
i
z
j
x
j
y
j
z
k
x
k
y
k
z
(10)
Advantageous is that the transformation matrix and its
derivatives can efficiently be computed. However, the
SOP are not enforced and alternatives II. and III. have
to be employed: Matrix R should form an orthonor-
mal basis and have determinant +1. Both constraints
are added to the residual.
The parameter vector of the Euler-Angles-
Parametrization is
~
a
R
=
φ
x
φ
y
φ
z
T
. The ro-
tation matrix is composed of three consecutive rota-
tions around the coordinate axis:
R
E
= R
φ
z
R
φ
x
R
φ
y
=
c
y
c
z
− s
x
s
y
s
z
−c
x
s
z
c
z
s
y
+ c
y
s
x
s
z
c
y
s
z
+ c
z
s
x
s
y
c
x
c
z
s
y
s
z
+ c
y
c
z
s
x
−c
x
s
y
s
x
c
x
c
y
(11)
with c
x
= cosφ
x
, c
y
= cosφ
y
, c
z
= cosφ
z
, s
x
= sinφ
x
,
s
y
= sinφ
y
and s
z
= sinφ
z
. The SOP are therefore en-
forced prior to optimization. Disadvantageous is the
well-known gimbal lock and the extensive usage of
trigonometric functions.
The parameter vector of the Quaternion-
Parametrization is
~
a
R
=
w x y z
T
. The
transformation matrix is composed by using a unit
quaternion q : (w,x,y,z) ∈ H with rotation axis
v = (x,y,z)
T
and rotation angle φ = 2arccosw:
R
Q
=
w
2
+ x
2
− y
2
− z
2
2(xy− wz) 2(xz+ wy)
2(xy+ wz) w
2
− x
2
+ y
2
− z
2
2(yz− wx)
2(xz− wy) 2(yz+wx) w
2
− x
2
− y
2
+ z
2
(12)
Since q has to be a unit quaternion, the SOP are not
completely enforced and alternatives II. and III. have
to be employed with |q| = 1 added to the residual. It is
cogitable to substitute e.g. w in terms of x, y and z as
w =
p
1− x
2
− y
2
− z
2
. Disadvantageous with quater-
nions is that there exist complex solutions for w.
The parameter vector of the Rodrigues’-
Formula-Parametrization is
~
a
R
=
x y z
T
.
The rotation matrix is composed by a rotation axis
~v = (x,y, z)
T
and a rotation angle φ = |~v|:
R
R
=
cosφ + x
2
c
φ
xyc
φ
− zs
φ
ys
φ
− xzc
φ
zs
φ
+ xyc
φ
cosφ + y
2
c
φ
yzc
φ
− xs
φ
xzc
φ
− ys
φ
xs
φ
+ yzc
φ
cosφ + z
2
c
φ
(13)
with c
φ
=
1−cosφ
φ
2
, s
φ
=
sinφ
φ
and φ =
p
x
2
+ y
2
+ z
2
,
or in case of φ = 0 it holds R
R
= I
3
. The SOP are
guaranteed by this parametrization.
8 SCALING
In general, due to discretization and erroneous match-
ing we cannot rely on perfect correspondences.
Therefore, the weight of each correspondence be-
comes crucial for the estimated result as unequal
weights shift the minima of the squared sum (Eq. 8)
to different positions. In order to find the optimal
least-squares value for all given correspondences, the
dimensions of all entries of the residual have to be
equal. Except for the Angle-/Distance-Error, all er-
ror measurements and SOP have a dimension of ei-
ther pixel or camera points, and scaling factors for the
corresponding other dimension can easily be derived
using the given camera matrix.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
274

9 GEOMETRICAL
CONFIGURATION
The pose problem can be solved with a finite number
of solutions when at least three point correspondences
are known (Fischler and Bolles, 1981), but there may
exist up to four possible solutions. Using four cor-
respondences the pose can be solved with a unique
solution only when the correspondences are in copla-
nar configuration (Gao and Tang, 2006). Otherwise
up to five solutions are possible. For five correspon-
dences still up to two solutions may occur when they
are not in coplanar configuration. Thus, when using
a minimal number of four or five correspondences a
coplanar configuration should be assured to prevent
multiple solutions. Additionally, the correspondences
should not be in degenerate configuration, i.e. they
are linearly dependent. For six or more linearly in-
dependent point correspondences in arbitrary config-
uration the pose problem becomes unambiguous. For
coplanar lines a finite solution is also feasible with at
least three lines. For a non-coplanar configuration at
least four lines are required. They must not be in de-
generate configuration, i.e. more than two lines are
parallel or intersect in one point (Christy and Horaud,
1999). Due to the known 3D data of the model, for
each correspondence the geometrical relationship to
the others in the correspondence set can be surveyed.
Table 1: Possible number of solutions for several numbers
of point correspondences and their configuration.
#correspondences non-coplanar coplanar
3 - 4
4 5 1
5 2 1
≥6 1 1
To check for linear dependency, i.e. three points
located on one straight line, the dot product of the
normalized direction vectors from one point to the
other two is calculated. If it becomes close to 1, the
correspondence will be rejected for pose estimation.
To check for coplanarity, a plane is calcuated from
the normalized direction vectors of three points. The
vector of the remaining fourth point is then inserted
into the equation of the plane. If the four points are
in coplanar configuration, the solution will be unique
and the correspondences are accepted as input data.
For straight lines linearly dependent configura-
tions occur if more than two lines are parallel or inter-
sect in one point. Parallelism is checked for by cal-
culating the dot product of the normalized direction
vectors of the lines. If all products are close to 1, the
lines are linearly dependent and the line correspon-
dences will be rejected. To check for a common inter-
section point, the intersection point of each line pair
is calculated respectively. If two or more intersection
points exist and the euclidean distance between these
points is below a predefined threshold, the lines are
collinear and will not be candidates for input data.
10 RESULTS
We tested combinations of error measurements and
parametrizations using points, lines and mixed corre-
spondences for the non-linear estimator. For the ex-
periments with synthetical data at an image resolution
of 640 x 480 pixel we used a unit cube around the ori-
gin; the initial camera pose was (0, 0,−5)
T
. In the
test sequence the camera was rotated by 30
◦
about the
axes of the world coordinate system and translated by
the vector (1, 1,1)
T
. Using this pose the correspon-
dences were established by perspective projection of
the 3D model features to the image plane, followed
by adding uniformly distributed noise in the range of
[0,10] pixel of displacement in arbitrary direction. We
regarded mean error and standard deviation between
real and estimated pose for translation, rotation and
number of iterations over 100.000 tests.
On points the comparison of error measurements
indicates that the image based Reprojection-Errorper-
forms more accurately than the Object-Space-Error
and Normal-Error for all possible combinations with
pose parametrizations. This can be explained by a
potentionally higher weighting of points in the ob-
ject space when they are more distant from the cam-
era center. The number of iterations is compara-
ble for all types of error measurement. Concerning
parametrization, Euler computation is slightly slower
while quaternions perform somewhat better, but lead
to less accurate translation estimation. For line cor-
respondences, the Angle-Distance-Error causes bad
pose results and a higher computation time. Line- and
Plane-Error are comparable for all parametrizations,
regarding accuracy and speed. Quaternions show a
slightly better computational performance.
Therefore, we propose Rodrigues’-Formular-
Parametrization together with Reprojection- and
Line-Error for combined non-linear pose estimation.
This combination shows the smallest pose error with-
out noticeable decrease in speed. In addition, using
pixel space error for both feature types, scaling is
not necessary to compensate for depth differences be-
tween the correspondences. The Rodrigues’-Formula
proves to be the best parametrization because inde-
pendent of the chosen error measurement it does not
influence pose accuracy. It is gimbal-lock free and
PARAMETER AND CONFIGURATION ANALYSIS FOR NON-LINEAR POSE ESTIMATION WITH POINTS AND
LINES
275

complies with the constraints of a rotation matrix by
definition. Thus, there is no need for additional en-
tries in the residual vector to be minimized during op-
timization and no singular value decomposition has to
be run afterwards to correct the result.
We also tested the influence of combining both
feature types under our proposed parameters. We
combined a minimal number of six correspondences
of one feature type with several numbers of the other
one and added several levels of noise. A pose esti-
mated by points is improved in rotation and transla-
tion by adding line correspondences independently of
the displacement error in the given point correspon-
dences. The improvement of the estimate converges
when at least six line correspondences are added to
the point correspondences. In the opposing case ad-
ditional point correspondences show a positive im-
pact on the exactness of a pose estimated with lines
only when the underlying line correspondences are
very noisy. This is due to a generally higher stability
of line features concerning displacement error. Point
features will be affected more strongly by growing
correspondence errors than lines. We can state that
a combination of point and line features is useful in
practical application to stabilize the estimated pose,
especially when there is only a minimal set of corre-
spondences available.
The resulting optimal estimator was successfully
run on a real test scene for verification of real-time
capabilities. The estimator pass for combined input
with point and line correspondences took about 1 ms
CPU time. The combination of both feature types did
not reduce computational speed, thus real time appli-
cation is ensured. Further, it could be seen that the
required number of iterations depends to a large de-
gree on the error level of the correspondences, while
it is hardly influenced by the total number of corre-
spondences.
11 CONCLUSIONS
We analyzed the best parameter choice for a non-
linear pose estimator when using a combined input
of point and line correspondences. Test results show
that the error measurement in pixel coordinates is su-
perior to the error in object space for points as well
as for lines. Further, it is proved that a parametriza-
tion may be chosen which fulfills the constraints of a
rotation matrix without requiring additional computa-
tional load. For points and lines this is the case with
Rodrigues parametrization. An optimal non-linear
estimator can be constructed by these propositions
working on an arbitrary number and choice of feature
type with a minimal set of three correspondences. The
estimator will improve the pose by considering the
configuration of the combined input data and select-
ing those point and line correspondences only, which
are proved to deliver unambiguous results.
ACKNOWLEDGEMENTS
This work was supported by grant no. MU 2783/3-1
of the German Research Foundation (DFG).
REFERENCES
Ansar, A. and Daniilidis, K. (2003). Linear Pose Estimation
from Points or Lines. In IEEE Transactions on Pattern
Analysis and Machine Intelligence, volume 25, pages
578–589.
Christy, S. and Horaud, R. (1999). Iterative Pose Compu-
tation from Line Correspondences. Computer Vision
and Image Understanding, 73:137–144.
Dornaika, F. and Garcia, C. (1999). Pose Estimation using
Point and Line Correspondences. Real-Time Imaging,
5:215–230.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: a paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM, 24:381–395.
Gao, X.-S. and Tang, J. (2006). On the Probability of the
Number of Solutions for the P4P Problem. ournal of
Mathematical Imaging and Vision, 25:79–86.
Haralick, B., Lee, C.-N., Ottenberg, K., and Nlle, M.
(1994). Review and analysis of solutions of the three
point perspective pose estimation problem. Interna-
tional Journal of Computer Vision, 13(3):331–356.
Hu, Z. Y. and Wu, F. C. (2002). A Note on the Number
of Solutions of the Noncoplanar P4P Problem. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 24:550–555.
Kumar, R. and Hanson, A. (1994). Robust methods for es-
timating pose and a sensitivity analysis. Computer Vi-
sion Graphics and Image Processing: Image Under-
standing, 60(3):313–342.
Lepetit, V., Moreno-Noguer, F., and Fua, P. (2009). EPnP:
An Accurate O(n) Solution to the PnP Problem. Inter-
national Journal Of Computer Vision, 81:155–166.
Lowe, D. (1991). Fitting parameterized three-dimensional
models to images. In IEEE Transactions on Pattern
Analysis and Machine Intelligence, volume 13(5),
pages 441–450.
Lu, C.-P., Hager, G., and Mjolsness, E. (2000). Fast and
Globally Convergent Pose Estimation from Video Im-
ages. IEEE Transactions on Pattern Analysis and Ma-
chine Intelligence, 22(6):610–622.
Wolfe, W. J., Mathis, D., Sklair, C. W., and Magee, M.
(1991). The Perspective View of Three Points. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 13:66–73.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
276
