
MULTIPLE OBJECT TRACKING WITH RELATIONS
Luca Cattelani
1
, Cristina Manfredotti
2
and Enza Messina
1
1
DISCo, Computer Science Dept., University of Milano-Bicocca, Viale Sarca 336, 20100 Milano, Italy
2
Image Group, E-Science Centre, Dept. of Computer Science (DIKU), University of Copenhagen,
Universitetsparken 5, DK-2100 Copenhagen, Denmark
Keywords: Sequential Monte Carlo, Particle filter, Relational particle filter, Multi-target tracking, Relational dynamic
Bayesian network.
Abstract: Dealing with multi-object tracking raises several issues; an essential point is to model possible interactions
between objects. Indeed, while reliable algorithms for tracking multiple non-interacting objects in
constrained scenarios exist, tracking of multiple interacting objects in uncontrolled scenarios is still a
challenge. The multiple-object tracking problem can be broken down into two subtasks: the detection of
target objects, and the association between objects along time. Interaction between objects can yield
erroneous associations that cause the interchange of object identities, therefore, the explicit recognition of
the relationships between interacting objects in the scene can be useful to better detect the targets and
understand their dynamics, making tracking more accurate. To make inference in relational domains we
have developed an extension of particle filter, called relational particle filter, able to track simultaneously
the objects in the domain and the evolution of their relationships. Experimental results show that our method
can follow the targets’ path more closely than standard methods, being able to better predict their
behaviours while decreasing the complexity of the tracking.
1 INTRODUCTION
Tracking of multiple interacting objects is a
challenging task due to the difficulties in
establishing the correspondence between objects and
observations. Particle filtering (PF) is appealing in
performing this task because of its ability to carry on
multiple hypotheses. Direct application of PF on
multiple object tracking, however, may lead to
unsuccessful tracking when unexpected events arise,
such as outliers, occlusions or discontinuities in
object dynamics.
Multi-object tracking usually uses a prediction
scheme that infers the number and locations of
targets from the available signals at each time step
independently. It usually involves either a generative
model of the signal given the target presence or a
discriminative machine learning-based algorithm.
However, unlike the single object tracking, it
requires to associate signal observations into the
most likely predicted trajectories.
Unfortunately estimating the family of
trajectories exhibiting maximum a posteriori
probability is an NP-Complete problem. This
problem has been dealt in the literature either with
sampling and particle filtering (Giebel, Gavrila &
Schnorr, 2004), or linking short tracks generated
using Kalman filtering (Perera, Srinivas, Hoogs,
Brooksby & Wensheng, 2006), or by greedy
dynamic programming in which trajectories are
estimated one after the other (Fleuret, Berclaz,
Lengagne & Fua, 2008).
In the literature various approaches to extend
models for a greater support to relations between
objects have been proposed. In particular, in
(Copsey & Webb, 2002) the use of Bayesian
networks for the representation of contextual
information in multi-target tracking is supported
while in (Khan, Balch & Dellaert, 2004) classic
particle filter is extended to take activities involving
target interactions into account.
In this paper, we address the problem of tracking
an unknown number of objects extending previous
works based on relational dynamic Bayesian
networks (RDBNs). RDBNs aim at simultaneously
modelling both object dynamics and possible
relations between objects (Manfredotti & Messina,
2009).
459
Cattelani L., Manfredotti C. and Messina E..
MULTIPLE OBJECT TRACKING WITH RELATIONS.
DOI: 10.5220/0003856004590466
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods (IATMLRP-2012), pages 459-466
ISBN: 978-989-8425-98-0
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

With the term “relation” we mean a property that
relates two or more objects and “relational” means
that the system state is modelled not only by
constituent objects and their attributes, but also by
their relations with other objects. Relations may
abstract real-world concepts such as moving
together/in formation, operating for a common goal,
being part of the same or of different groups,
participating in an activity with given roles, etc. The
inference task is then performed through a particle
filter approach that traces not only objects but also
their relations. Tracking relations may help both to
improve the quality of positions filtering, and to
infer more complex activities accomplished by
objects (Manfredotti, Fleet, Hamilton & Zilles,
2011).
In particular, the problem of tracking groups of
targets (i.e. targets with similarity in positions and
speeds) has been addressed in several works. One of
the first of these approaches represents relations
between moving objects as physical forces as in
Boids (Reynolds, 1987). This approach, although not
originated from tracking applications, has inspired
different tracking algorithms
that represent groups
of targets, among others (Pang, Li & Godsill, 2008)
and (Gning, Mihaylova, Maskell, Pang & Godsill,
2011) that model groups of targets as evolving
graph networks: graph structures that explicit
specific one-to-one relations between the group
members.
By using relational Bayesian networks, we allow
the representation not only of groups but also of
arbitrary relations between moving objects. We
compare the performance of our approach with the
standard particle filtering algorithm, and show that
using relations improves the quality of tracking.
2 TRACKING WITH RELATIONS
The proposed approach for multi-target tracking
consists of statistically modelling not only target
positions but also the relations that may exist
between two or more targets. We first describe the
general Bayesian framework for tracking multiple
objects, then in subsection 2.1 we outline the
sequential Monte Carlo method known as particle
filtering, and finally in 2.2 we extend this method to
a relational domain.
The aim of the tracking task is to infer the
posterior probability for the state at time ,
,
starting from the whole history of sensor data
:
.
(
|
:
)
(1)
Under the Markov assumption, we can state that
the probability of
depends only on
and
.
(
|
:
)
=(
|
,
)
(2)
Another assumption commonly applied to
tracking is the conditional independence of the
observation on the state.
(
|
:
,
:
)
=(
|
)
(3)
In a Bayesian framework, equation (3) represents
the sensor model, which may be seen as a measure
of the sensor reliability. Indeed, depending on the
type of sensors, observations may be imprecise,
lacking information or erroneous.
Under the assumptions (2) and (3) introduced
above, it is possible to write:
(
|
:
)
=
=
(
|
)
(
|
)(
|
:
)
(4)
where is a normalization factor.
Together with the sensor model, the distribution
used to model (
|
) is a fundamental element
for a Bayesian tracker and is called evolution model.
Figure 1: Transition model. Arrows indicate probabilistic
dependence between variables.
In this paper, we are interested in evolution and
sensor models that are not linear. In these settings,
one cannot expect to find a closed form solution to
the filtering problem as the well-known Kalman
update equation. We therefore, consider the
approximate solution to the filtering problem given
by the particle filtering algorithm (described in the
following). Moreover, the problem we are dealing
with aims at tracking an unknown number of targets,
consequently, particles contain also information
about this number.
2.1 Particle Filtering
Particle filters, also known as sequential Monte
Carlo methods, are estimation techniques based on
simulation. A particle filter uses a collection of
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
460

particles, which are hypothesis on the state of the
system, to represent a probability distribution on the
state of the system itself.
Particles are composed of two parts: a state,
which is a point in the state space of the system, and
a weight representing the approximation of the
posterior probability. A particle filter, as any
Bayesian filter, makes use of two probabilistic
models: an evolution model, which defines the
probability that a given state at time −1 evolves in
another state at time , and a sensor model, which
defines the probability of a state given the
observations.
When a new observation becomes available,
three mayor steps are executed.
Forecasting. Using the evolution model, each
particle at time −1 is evolved in a particle at
time . The evolution model includes a
random noise component.
Weighting. Using the sensor model, particles
are weighted according to the conditional
probability of the observation given the state
represented by the particle.
Resampling. By means of a resampling
algorithm, some particles are discarded while
others are repeated based on their weight.
Resampling algorithm called “residual
sampling” (Liu & Chen, 1998) is used in our
experiments.
At the end of each iteration, the new collection
of particles represents the posterior probability of the
states of the system once the information about the
last observation has been incorporated.
2.1.1 Tracking an Unknown Number of
Objects
Multi-object tracking is even more challenging when
the evidence has to be associated with an unknown
number of objects. In this paper we deal with this
problem by assuming that the state dimension can
dynamically change with respect to the number of
objects present in the scene. Indeed, when a new
object appears, its attributes and relations become
part of the state. To avoid the potential quadratic
growth of the state dimension, we assume that each
object may be in relation with a limited number of
other objects (this assumption is reasonable for
many applications). On the other hand, when an
object disappears from the scene the state is
modified accordingly by removing attributes and
relations associated with that object. In order to deal
with occlusions we consider a time window during
which the object is maintained despite the evidence
does not reveal it and its position and the relations
associated with it are updated using the forecast
model. The time window length may vary depending
on the application considered and may also depend
on the belief that the object is occluded. If the object
reappears in the scene then the sensor model is used
to update its attributes and relations.
2.2 Relational Particle Filtering
In order to consider relations between targets in
(Manfredotti & Messina, 2009) an algorithm called
relational particle filter has been presented. It
extends the standard particle filter algorithm to
relational domains. We exploit this approach with
the aim of keeping computational complexity under
control while tracking an unknown number of
targets.
In a relational domain, the state of the system
can be divided in two parts: the state of the attributes
of the objects, and the state of the relations between
the objects.
=<
,
>
(5)
When applied to tracking an unknown number of
targets,
contains attributes of the targets, while
relations between the targets.
To apply the relational particle filtering three
main assumptions have to be made:
a) relations are not directly observable, i.e.
(
|
,
)
=(
|
)
(6)
b) relations at time depend only on relations
at time −1 and attributes at time , so they
are not directly dependent on attributes at
time −1, i.e.
(
|
:
,
:
,
:
)
=(
|
,
)
(7)
c) attributes at time depend on attributes and
relations at time −1 but not on relations at
time , i.e.
(
|
:
,
:
,
:
)
=(
|
,
)
(8)
Taking into account the nature of relations, these
assumptions are reasonable in practice.
MULTIPLE OBJECT TRACKING WITH RELATIONS
461
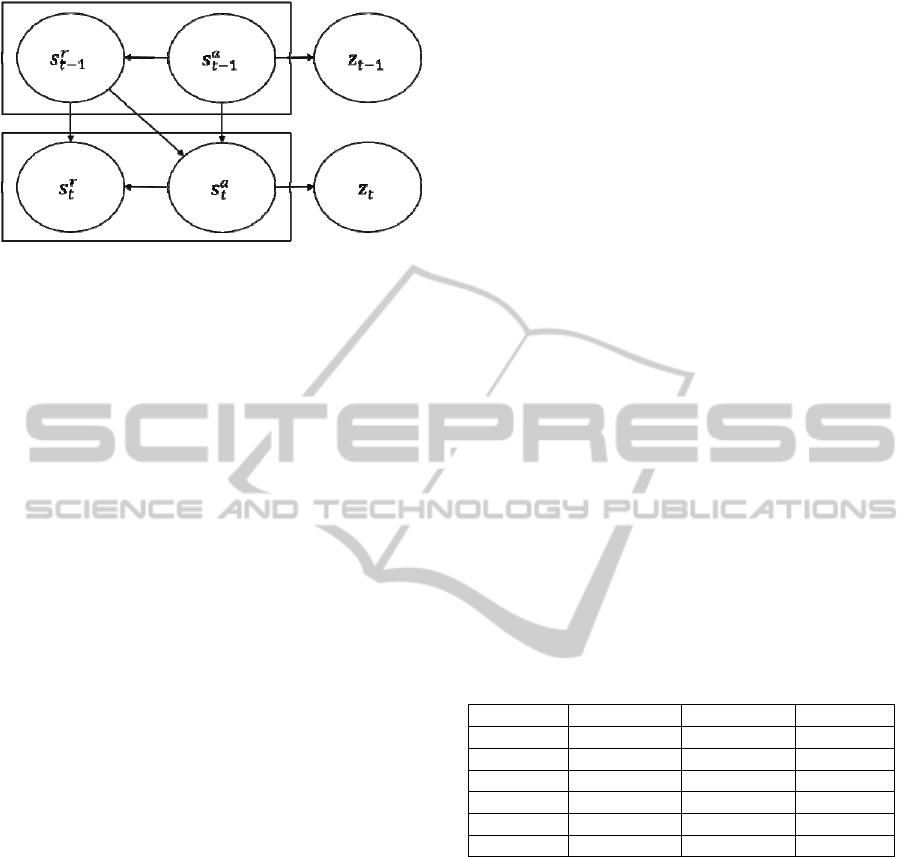
Figure 2: Relational transition model. Arrows indicate
probabilistic dependence between variables.
With relations the tracking problem is
reformulated as the problem of finding
(
,
|
:
)
,
(9)
while (2) and (3) become respectively
(
,
|
:
)
=
(
,
|
,
,
)
,
(10)
(
|
:
,
:
,
:
)
=(
|
,
).
(11)
Applying (6) to (11), we can write:
(
|
:
,
:
,
:
)
=
(
|
)
.
(12)
With the reformulation in (9), the (4) becomes
(
,
|
:
)
=
(
|
,
)
(
,
|
,
)
(
,
|
:
)
,
(13)
and applying the assumptions about relations
(
,
|
:
)
=
(
|
)
(
|
,
)
(
|
,
)
(
|
,
)
(14)
For more details, see (Manfredotti, Fleet &
Messina, 2009).
In order to implement a relational particle filter
we need to modify the evolution model while the
sensor model and the resampler may remain
unchanged. This is possible because the resampler
works only on the weights of the particles, while
relations are assumed to be not directly observable,
and thus not included in the sensor model, as in
equation (6).
In the following section, we validate the
approach on video sequences for tracking persons
moving together under different conditions such as
occlusion and disappearance.
3 EXPERIMENTS
The proposed relational approach is validated on a
benchmark dataset from the CAVIAR Project (the
CAVIAR database, and the associated ground truth
data is available for download at http://homepages.
inf.ed.ac.uk/rbf/CAVIAR/). For our analysis, we
considered video sequences where pedestrians are
walking inside a mall.
We considered the relation “walking together”,
assuming that related targets have some common
movement pattern (typically, some form of cohesion
and common direction). Therefore, if we know that
two pedestrians are walking together and one of the
two (but not both) become occluded we can assume
that the occluded target is walking near the other and
use this information for evolving his/her position in
absence of new observations.
In the following subsections we present the filter
input data, the evolution and sensor models, and
experimental results.
3.1 Input Data
The data set we consider contains 26 videos, all
registered from the same camera. Their codes are
listed in Table 1.
Table 1: Ground truth file names related to considered set
of videos.
cwbs1gt ceecp1gt ceecp2gt cols1gt
cols2gt colsr1gt colsr2gt cosow1gt
cosow2gt cose1gt Cose2gt cosme1gt
cosme2gt cosmne1gt cosmne2gt cosne1gt
cosne2gt csa1gt csa2gt c3ps1gt
c3ps2gt c2es1gt c2es2gt c2es3gt
c2ls1gt c2ls2gt
The camera is placed above a corridor in the
mall, looking in the corridor direction slightly from
above (see Figure 3). The corridor opens on other
corridors and shops. There are columns occluding
view on the right. Frames have a resolution of
384 x 288 pixels and a frequency of 25 frames per
second.
This camera has been chosen because regarded
as the most significant of the available three cameras
to validate group tracking. Characteristics taken into
account where:
frequent presence of a variable number of
pedestrians walking together;
presence of critical situations for tracking,
such as target disappearances and
reappearances after a number of frames, and
partial target occlusions.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
462
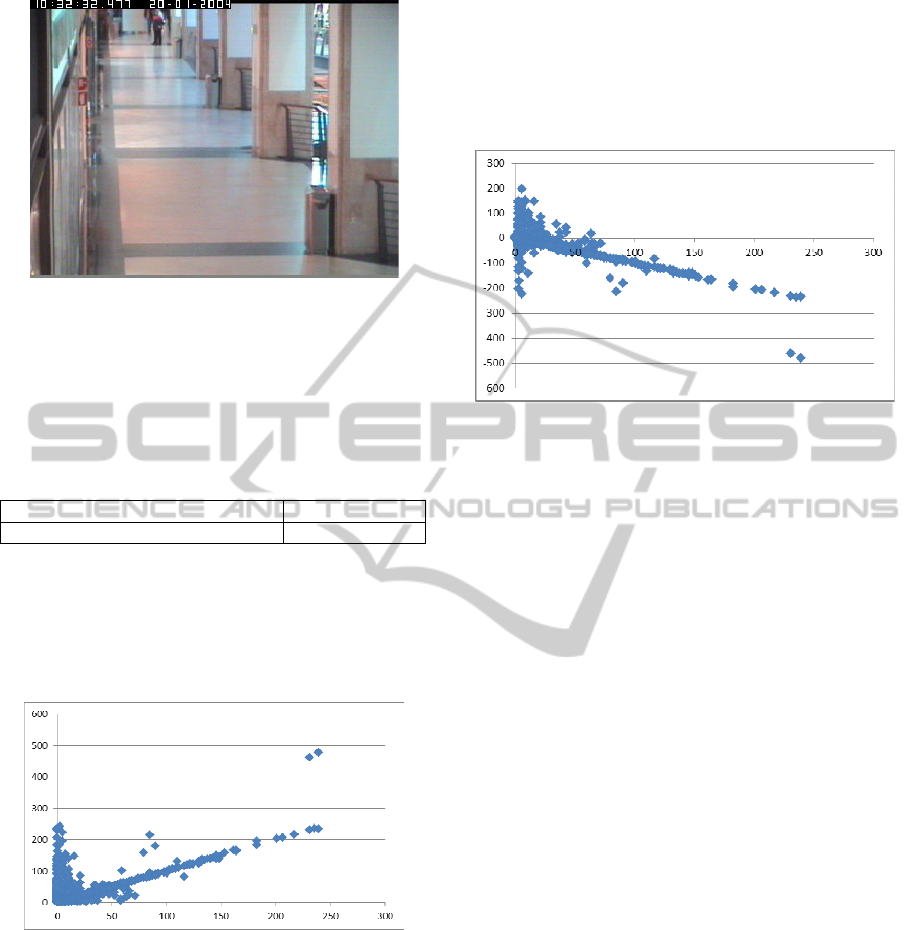
Figure 3: Camera view.
Average speed and speed variation of the targets
for the videos considered (listed in Table 1),
computed as the absolute value of the differences
between the speed at two consecutive time steps, are
reported in Table 2.
Table 2: Input data analysis.
Average speed 1,07 m/s
Average speed variation 1,83 m/s
Figure 4 reports the variation in speed against
speed. From this figure, we can see that there is an
average speed variation that is even bigger than the
average speed. This is caused by the nature of
pedestrian locomotion but also by the kind of frames
pre-processing before tracking.
Figure 4: Speed variation norm given speed norm. Speed
on x-axis, speed variation on y-axis. X-axis values are
from 0 to 239 m/s while y-axis values are from 0 to 478
m/s.
In Figure 4 most of the samples have a speed
smaller than 2 m/s, while the rest is sparse with
respect to the speed value. Some of the sparse
samples are clearly sensor errors, because speed
and/or acceleration are unrealistic for pedestrians.
Nonetheless, the graph shows that many samples
present low speed but high acceleration, meaning
that a pedestrian is starting to move or there is a
sensor inaccuracy. On the other hand, samples with
high speed also exhibit high acceleration, usually
with opposite direction with respect to the target
motion, meaning that the pedestrian is rapidly
reducing his/her speed, or there is a sensor
inaccuracy. Speed variation relative to the direction
of motion is shown in Figure 5.
Figure 5: On x-axis the speed norm, in m/s. On y-axis the
speed variation component relative to the speed direction,
in m/s. Samples are collected on all data set, taking into
account the evolution between two subsequent frames.
Samples where speed is zero are not included because
there is no speed direction.
Inaccuracies of sensor and very high speeds and
accelerations in observations are principally due to
two reasons: (1) the approximation in pixel of the
bounding boxes of the pedestrians, that in turn
produces a loss in accuracy that increases with the
distance from the camera, and (2) partial occlusions,
producing erroneous target bounding boxes and thus
significant error in positioning of the target on the
2D floor plane.
To cope with these nonuniform movements we
define appropriate evolution and sensor models, as
described in the following subsections.
3.2 The Evolution Model
For each target, a particle maintains a state
composed of position, speed and relations with other
objects. Since we are considering the relation
“walking together”, we can assume that each
pedestrian belongs to a group of persons of size
greater or equal to one.
When a new target is added to a particle, its
initial placement and speed are chosen randomly, the
first from a normal distribution centred in the
position of the observation, the second from a
normal distribution centred in zero. In the relational
particle filter, we assume that a new target has equal
probability to belong to an existing group as to be
waking alone.
When the evolution model is applied to a target
MULTIPLE OBJECT TRACKING WITH RELATIONS
463

that was already present in the particle from a
previous step, the target acceleration is generated
from a random distribution that depends on its
speed, as shown in Table 3. Therefore, the evolution
model takes into account the fact that observations
of pedestrians have speed variations (as shown in
Figure 4) that increase with the increasing of the
speed.
Table 3: Speed variation distribution given speed.
A
Speed norm
cm/frame
B
Speed variation
mean norm,
m/frame
C
Speed variation
standard
deviation,
m/frame
0.00 – 0.05 0.0000 0.1345
0.05 – 10.00 0.0128 0.1541
10.00 – 20.00 0.1188 0.1786
20.00 – 30.00 0.1994 0.2792
30.00 or more 0.6090 1.1634
Target speed variation distribution given its
speed is learned from data and reported in Table 3
where in column A are reported the speed intervals,
and in column B and C are reported, respectively,
the mean speed variation and the associated standard
deviation, used to generate the sample speed
variation through a 2D normal distribution. The
values in column B are the norm of the mean vectors
of the 2D distribution, which direction is opposite
with respect to the speed vector of the target. This
guarantees that the average speed variation is placed
in the opposite direction with respect to the speed
direction, and that its norm and its variance augment
with the speed, as it happens in the data set (see
Figure 5).
What previously described completely covers the
evolution model applied in the non-relational
particle filter and in the relational particle filter for
targets walking alone. In the case of targets
belonging to the same group we compute the mean
value of their speed and then we add the speed
variation to each target independently (in this way,
each target gets a different speed variation vector).
3.3 The Sensor Model
In our experiments, we consider as observations the
positions of the pedestrians, which we approximate
on the 2D plane of the floor by taking the lowest
central point of the bounding box (provided by
CAVIAR data) and projecting it, by using an
extrapolated homomorphism starting from available
control points, to the floor plane. These operations
are a pre-processing step that we apply at each frame
before filtering, producing the input observations for
the particle filter.
In the sensor model used in our experiments,
which is the same both for the relational and non-
relational filters, we assume a normal distribution of
the position observations of each target with respect
to the ground truth.
To assign weights to the particles we use an
estimate of the probability that the particle
represents the real state. This is computed taking
every possible mapping of observation targets to
particle targets, for each mapping we compute the
probability that the particular mapping matches the
real state, according to the sensor model, and
summing the probabilities of all mappings together.
Then weights of all particles are normalized.
The probability of a mapping is obtained
multiplying the probability that every single target
matches the real state.
3.4 Results
All 26 videos of the data set where used to collect
the statistical information that was presented before
and that was used to tune the distributions of the
evolution and sensor models. On a subset of these
videos, experimental results were collected,
presented in the following. Figure 6 shows a frame
with overlapping bounding boxes, that are part of the
pre-processing, and particles projected on the
camera plane. In all experiments, both with
relational and non-relational filters, the same
parameters where used.
Figure 6: Frame with target bounding boxes and projection
of particles on camera plane (points near the base of the
targets). The upper two pedestrians are walking together.
The main result is that, in all executed
experiments, the relational filter performs better than
the non-relational one. We here report the results
related to two relevant videos, namely cosow1gt and
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
464
cosne1gt.
cosow1gt is a 55 seconds video with up to five
targets per frame. It presents pedestrians walking
together and pedestrians disappearing and
reappearing from inside shops. This second fact
causes partial occlusions, which in turn causes
critical errors in position observations.
Groups of ten runs, with varying random seeds,
where executed both with the relational and with the
non-relational particle filters, with 500, 1000, 2000
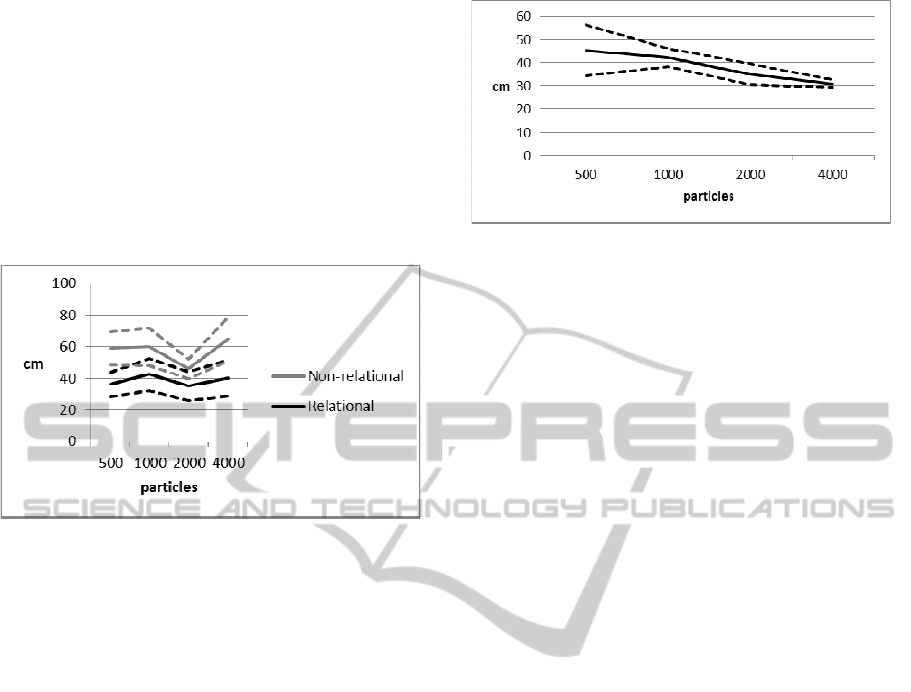
and 4000 particles. Results are shown in Figure 7.
Figure 7: Comparison between relational and non-
relational filters. Average error over 10 runs with different
numbers of particles in cosow1gt scenario. Dotted lines
are 95% confidence intervals.
The error reported in Figure 6 is the average
error on ten runs with the related 95% confidence
interval. In each run, the error is the sum of the
absolute error on all targets in all frames. It is
evident that the relational filter produces an error
significantly lower than the non-relational filter.
cosne1gt video has a duration of 28 seconds and
presents up to 3 targets. A pedestrian disappears
behind a pillar and reappears on the other side. This
causes also partial occlusions while disappearing
and reappearing. The complexity of cosne1gt
scenario caused the non-relational filter to be
particularly ineffective.
Figure 8 shows experimental results on cosne1gt
scenario using the relational filter. Ten runs where
executed with 500, 1000, 2000 and 4000 particles,
average error and 95% confidence interval are
plotted. Error and size of confidence interval reduce
increasing the number of particles. In this case, the
non-relational particle filter has very poor
performance, producing particles with very low
importance weights, and generating numerical
problems.
Figure 8: Error average and 95% confidence interval on 10
runs, repeated with varying number of particles, in
cosne1gt scenario with relational filter.
4 CONCLUSIONS AND FUTURE
WORK
In this paper, we used a modelling framework based
on relational dynamic Bayesian networks to
represent the dependencies between targets in the
context of multi-object tracking. An inference
algorithm able to take into account probabilistic
relations between interacting objects have been
applied for tracking people in video sequences.
A significant number of tests on real data, from a
publicly available benchmark data set, have been
performed with a rigorous measurement of filtering
quality. The benefits of adding relational
information to particle states have been
experimentally validated.
Experimental results show that the relational
approach outperforms the standard non-relational
methods. This work represents a step towards better
algorithms and models to provide inference in
complex multi-target systems also in the direction of
activity recognition.
This work may be expanded in different
directions, some proposals follow.
Just as using relations between targets
improves the tracking quality and gives
more information to the higher layers,
adding object goals (Manfredotti, Messina
& Fleet, 2009) too (like pedestrian goals) to
the particle states might provide a similar
benefit. A particle might contain the
information that a pedestrian, or group of
pedestrians, is going to a shop, and confront
this assumption with the observations in the
usual way. The property of “be going to the
shop X” will influence the forecasting step
of the particle filter, and thus increase or
reduce the fitness of the particle. For a
MULTIPLE OBJECT TRACKING WITH RELATIONS
465

representation of goals in a pedestrian
mobility model, see (Brambilla & Cattelani,
2009).
Doing computations for each possible
association of targets in the particle and
targets in the observation is very expensive,
since the computational complexity is
exponential in the number of targets. Less
expensive approximations might be
investigated.
An interesting challenge would be the
automatic extraction of relevant relations
starting from data. Similar results on
Bayesian networks and probabilistic
relational models exist (Getoor, Friedman,
Koller & Pfeffer, 2001).
REFERENCES
Brambilla M., Cattelani L., 2009. Mobility analysis inside
buildings using Distrimobs simulator: A case study. In
Building and Environment, Volume 44, Issue 3, March
2009, 595-604.
Copsey K., Webb A., 2002. Bayesian networks for
incorporation of contextual information in target
recognition systems. In SSPR/SPR, 709–717.
Fleuret F., Berclaz J., Lengagne R., Fua P., 2008. Multi-
Camera People Tracking With a Probabilistic
Occupancy Map. In IEEE Transactions on Pattern
Analysis and Machine Intelligence, Volume 30, no. 2,
February 2008, 267–282.
Getoor L., Friedman N., Koller D., Pfeffer A., 2001.
Learning probabilistic relational models. In S.
Dzeroski S. and Lavrac N. (Eds.), Relational Data
Mining, Springer-Verlag, Kluwer, 2001, 307-335.
Giebel J., Gavrila D., Schnorr C., 2004. A Bayesian
Framework for Multi-Cue 3D Object Tracking. In
European Conference on Computer Vision.
Gning A., Mihaylova L., Maskell S., Pang S. K., Godsill
S., 2011. Group Object Structure and State Estimation
With Evolving Networks and Monte Carlo Methods,
IEEE Transactions on Signal Processing, Vol. 59, No.
4, April 2011, 1383-1396.
Khan Z., Balch T. R., Dellaert F., 2004. An mcmc-based
particle filter for tracking multiple interacting targets.
In ECCV (4), 279–290.
Liu, J. S., Chen, R., 1998. Sequential Monte Carlo
methods for dynamic systems. In Journal of the
American Statistical Association, Volume 93, 1032-
1044.
Manfredotti C., Messina E., Fleet D. J., 2009. Relations to
improve multi-target tracking in an activity
recognition system. In 3
rd
International Conference on
Imaging for Crime Detection and Prevention, (ICDP-
09), London, December 2009.
Manfredotti C., Messina E., 2009. Relational Dynamic
Bayesian Networks to Improve Multi-Target Tracking,
In Lecture Notes in Computer Sciences ACIVS 2009,
Volume 5807, 528-539.
Manfredotti C. E., Fleet D. J., Hamilton H. J., Zilles S.,
2011. Simultaneous Tracking and Activity
Recognition with Relational Dynamic Bayesian
Networks, Technical Report CS 2011-1, March 2011.
Pang S. K., Li J., Godsill S. J., 2008. Models and
Algorithms for Detection and Tracking of Coordinated
Groups, In Aerospace Conference, 2008 IEEE, March
2008, 1-17.
Perera A., Srinivas C., Hoogs A., Brooksby G., Wensheng
H., 2006. Multi-Object Tracking Through
Simultaneous Long Occlusions and Split-Merge
Conditions. in Conference on Computer Vision and
Pattern Recognition, June 2006, 666-673.
Reynolds C. W., 1987. Flocks, herds and schools: A
distributed behavioral model. In Proceedings of the
14th annual conference on Computer graphics and
interactive techniques (SIGGRAPH '87), Maureen C.
Stone (Ed.), ACM, New York, NY, USA, 25-34.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
466
