A COMPRESSED DATA MODEL FOR A BITMAPPED XML
STRUCTURE
Mohammed Al-Badawi
Department of Computer Science, Sultan Qaboos University, Muscat, Oman
Keywords: PACD XML Technique, XML Processing, XML Compression, XML Clustering, Sparse Matrix
Compression, Bitmap Storage.
Abstract: Developments on XML processing usually produce tools to formulate both the XML data storage and the
associated query processor. PACD is one of such developments that stores the XML structure into a set of
n×n bitmap matrices each of which encodes a specific XML structure related to an XPath axis. The amount
of space and the complexity of storing uncompressed version of these matrices is large for huge XML
databases; and such requirements may go beyond the HW/SW capabilities; this justify the need for the data
compression model discussed in this paper.
1 INTRODUCTION
PACD, as a new bitmapped XML processing
technique, was initially introduced in (Al-Badawi et
al, 2009). The technique encodes the entire XML
structure into ten bitmap matrices each of which
corresponds to a certain XPath (Berglund et al.,
2010) axis. This paper discusses the specifications of
the data compression model (DCM) used by PACD
to reduce the amount of the storage space required
for storing the XML structure. The DCM illustrated
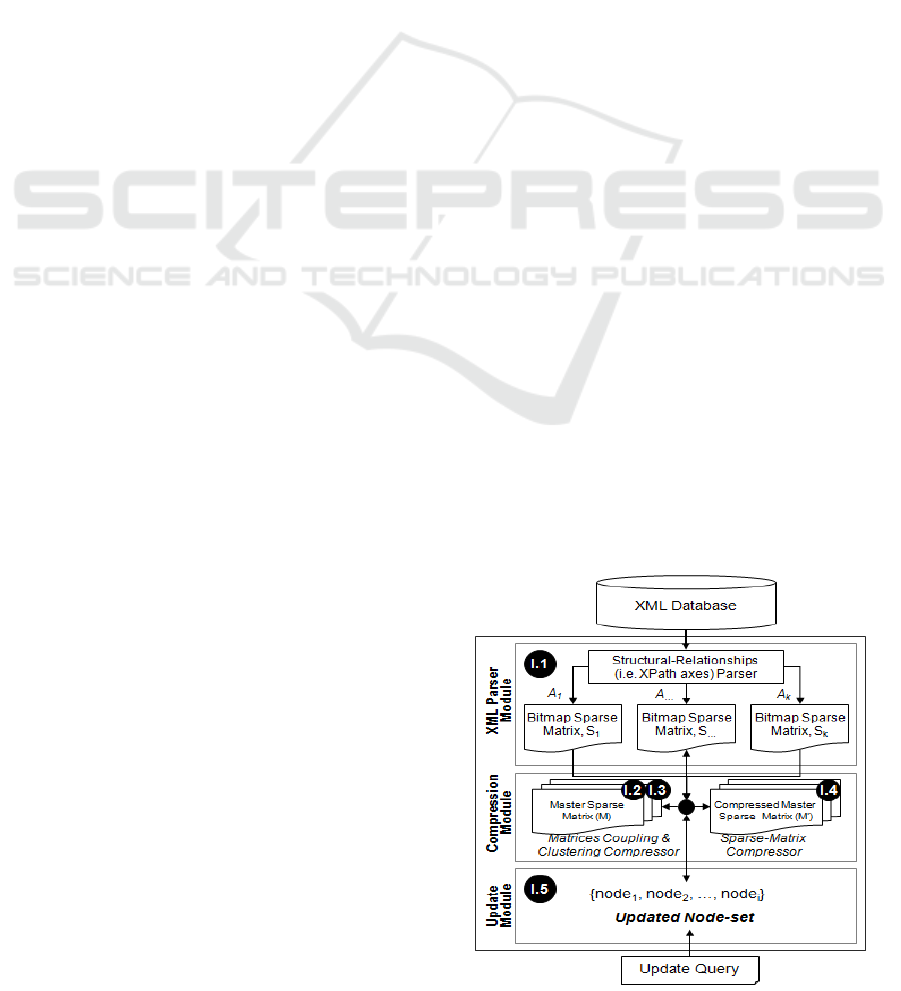
in Fig. 1, performs three compression processes to
the XML structure (labelled by I.2, I.3 and I.4 in Fig.
1) in order to reduce its complexity in terms of
storage requirements, representations layout and
data manipulations. The first process reduces the
number of the matrices encoded from ten to five
matrices by using a simple matrix transformation
algebra which facilitates 2-in-1 representations for
some related matrices. The second compression
process provides a method by which two or more
matrices can be combined into a single matrix called
a ‘master’ matrix. The process may generate
multiple master matrices which should preserve
specific characteristics of their composing matrices.
The third process is the sparse-matrix compression
process which employs one or more sparse-matrix
compression techniques to act over the master
matrices in order to compact their physical
representations. The sparse-matrix compression
should allow the compressed data to be managed
efficiently during the course of the query execution
and data update transactions.
The rest of this paper is organized as follows.
Section 2 briefly restates the specifications of PACD
and its data representation in Sections 2.1 and 2.2
respectively. The need for the proposed DCM is
justified in Section 2.3 while Section 3 discusses the
specifications of the PACD’s DCM including the
three compression processes that are performed over
the encoded XML structure. The paper is concluded
in Section 4.
Figure 1: PACD’s Index Builder (IB).
89
Al-Badawi M..
A COMPRESSED DATA MODEL FOR A BITMAPPED XML STRUCTURE.
DOI: 10.5220/0003895400890095
In Proceedings of the 8th International Conference on Web Information Systems and Technologies (WEBIST-2012), pages 89-95
ISBN: 978-989-8565-08-2
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 BACKGROUND
2.1 PACD Technique
PACD, introduced in (Al-Badawi et al, 2009), is a
bitmap XML processing technique consists of two
subsystems: the Index Builder (IB) and the Query
Processor (QP). The IB shreds XML data (including
the textual contents and the XML structure) into the
underlying data storage while the QP translates and
executes XML queries (expressed in XQuery
syntax) over the shredded XML data. Of the former,
the component performs three main operations
including the conversion of XML structural
relationships into a set of binary relations (bitmap
format), the compression of bitmapped XML
structure and the XML updates handling (see Fig 1).
During the first operation (process I.1 in Fig. 1), the
XML structural relationships (derived by the
XPath’s thirteen axes and their extension; the Next
and Previous axes(Al-Badawi et al, 2009) are
organized into a set of n×n matrices each is
representing a specific XML structure corresponding
to an XPath axis. The entries of the generated
matrices are binary where ‘1’ is indicating the
existence of the structural relationship (e.g. child,
parent, …etc) while ‘0’ is indicating the absence of
such relationship between any node pairs (Wang et
al., 2006; He et al., 2005). In the XML databases
context, these matrices are sparse (Sun et al., 2008;
George et al., 1993) and their dimensions are huge
can go beyond any hardware and software limits.
This justifies the need of the proposed Data
Compression Model (DCM).
2.2 Encoding XML Structure in PACD
As mentioned above, PACD explicitly encodes the
whole XML structure represented by XPath axes
into a set of bitmap matrices . Two main advantages
of such encoding are: a) to increase the QP coverage
and b) to reduce the overhead workload caused by
deriving some XML structures from others
(Pettovello and Fotouhi, 2006).
XPath/XQuery (Berglund et al., 2010; Boag et
al., 2010) specification describes 13 axes for any
context node in the XML tree. These are the self,
child, parent, descendant, self-or-descendant,
ancestor, self-or-ancestor, preceding, following,
preceding-siblings, following-siblings, attributes and
namespace axes. Additionally, PACD introduced the
‘next’ and ‘previous’ axes to substitute the
following-sibling and preceding-sibling in
preserving the document order (Al-Badawi et al,
2009). The process of mapping XML structure into
bitmap matrices explicitly excludes the ‘namespace’
axis due its popularity in XML database
transactions, combines the ‘self-or-descendant’ with
the ‘descendant (and ‘self-or-ancestor’ with the
‘ancestor) into a single matrix respectively, and
encodes attributes as ordinary child-entries in all
matrices. Furthermore, PACD deals with the ‘self’
axis at the XML processing level (i.e. querying and
updating) instead of encoding this structure
explicitly in a separate matrix
As for illustration, Fig. 2 depicts a sample XML
database while Fig. 3 and Fig. 4 respectively show
the childOf and descendentOf matrices for the XML
tree as an example of the XML/matrix
transformation.
<dblp>
<book year=“2001”>
<title>Data on the Web</title>
</book>
<book key=“110”>
<author>
<first>John</first>
<last>Smith</last>
<author>
</book>
<thesis key=“500”>
<title>A Bit…</title>
</thesis>
</dblp>
Figure 2: An XML database example.
2.3 The Need for Data Compression
It is clear from the above discussion that the size of
the PACD’s data storage for large XML databases
will be huge in terms of matrix dimensions and
physical storage space. This could result in several
performance issues such as HW/SW failure and
processing deficiencies. One way to overcome such
limitation is to have the PACD’s data storage
reduced by the all means while keeping its XML
structure coverage still comprehensive.
A such proposal can also benefit the following
aspects:
¾ Memory Based Management: is an attractive
approach since it eliminated overhead caused by
perform I/O operations. To achieve this, XML
literature has produced different data compression
techniques including data guide summaries
(Goldman and Widom, 1997; Haw and Lee, 2009),
adaptive indexes (Chung et al., 2002), and selective
indexes (Milo and Suciu, 1999; Hammerschmidt,
2005). The compression architecture of these
techniques takes place at the XML encoding level
WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies
90
&0 &1 &2 &3 &4 &5 … &11
&0000000…0
&1100000…0
&2010000…0
&3010000…0
&4100000…0
&5000010…0
………………………
&11000000…0
&0 &1 &2 &3 &4 &5 … &11
&0000000…0
&1100000…0
&2110000…0
&3110000…0
&4100000…0
&5100010…0
………………………
&11100000…0
Figure 3: The childOf Matrix. Figure 4: The descendentOf (or descOf) Matrix.
Figure 5: The framework of the PACD’s data compression model for the XML structure.
rather than the data representation level which in
turn results in some other performance issues such
as summary expressiveness. PACD redeems such
shortcoming by encoding the full XML structure and
incorporates well established compression
techniques to reduce the size of encoded
information.
¾ Database Sizing: In this context, database
sizing describes the process of controlling the size of
the database in order to utilize the computer
system’s resources during the database management
(McCord, 1981; O’Neil and O’Neil, 2001). Loading
‘x’ storage units (e.g. byte) is often faster than
loading ‘x+y’ storage units (N.B.: other factors, such
as the desirable data location, are also involved but
the same logic applies). Therefore, there is no doubt
that the compressed data will outperform the un-
compressed data provided that the same database’s
functionalities are obtainable from both versions,
and the data compression complexity is kept to the
minimum.
¾ Nature of Data Presentation: Finally, the
amount and type of information stored by PACD
necessitates the use of data compression techniques.
PACD aims to store the XML structures using a
bitmap based representation which is encoded into
sparse-matrices. The system creates ten sparse
matrices (see next section) for this purpose, each of
which requires ‘n×n’ storage units. The total figure
for storing these matrices, as well as XML’s textual
contents, becomes huge for large XML databases
and could be beyond the capabilities of the
ACOMPRESSEDDATAMODELFORABITMAPPEDXMLSTRUCTURE
91

underlying hardware and software specifications; or,
it could result in other performance issues.
3 A DATA COMPRESSION
MODEL
To achieve a better data storage performance PACD
maintains separate models for compressing the XML
textual contents and the XML structure respectively.
This paper only describes the mechanism used to
compress the XML structure.
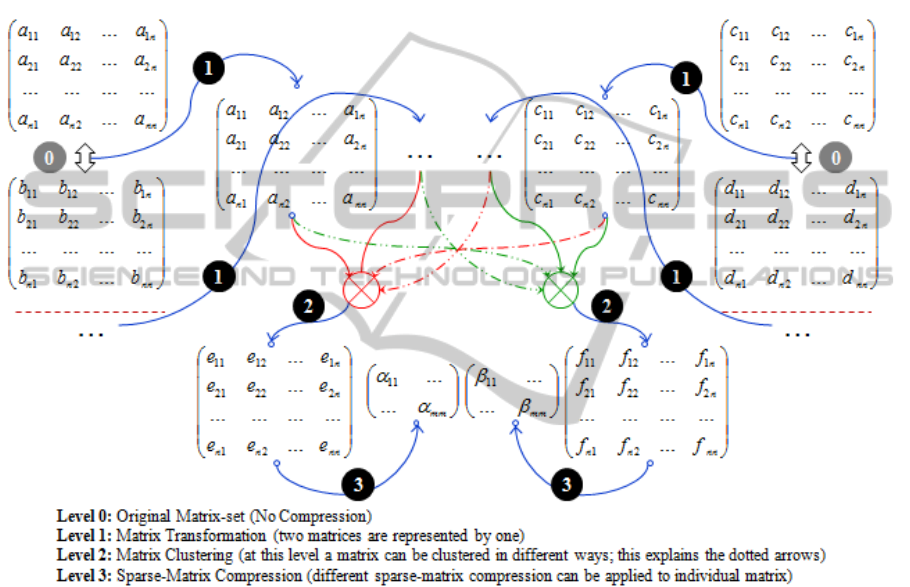
3.1 Model Overview
The PACD’s matrix based storage (or XML
structure storage) can be compressed using three
different types of matrix operations. These are
matrix transformation operations to derive some
matrices from other matrices; matrix clustering
operations to combine a set of matrices into one
matrix; and sparse-matrix compression techniques to
further reduce the storage space requirement of the
final matrix set. The layout of the overall XML
structure compression is illustrated in Fig. 5 while
each of these levels is briefly described in the
subsequent sections.
3.2 A Matrix Algebra
To formulate data compression model transactions,
each matrix will be represented as a set and the
group of sets are then manipulated (e.g. transformed)
using set-theory notations. A set, corresponding to a
specific PACD’s matrix, contains the positive entries
of that matrix encoded as node pairs. For example,
the entries of the childOf set of the above XML tree
are {(&1,&0), (&4,&0), (&9,&0), (&2,&1), …,
(&11,&9)}.
On the other hand, XML structures reflected by
the thirteen XPath’s axes and their extensions the
‘next’ and ‘previous’ axes, are encoded into ten
sparse matrices as proposed earlier. According to the
XPath’s specification (Berglund et al., 2010), these
axes are found in invertible and/or inclusive pairs
and hence their sparse-matrix and set
representations. Based on this logic, the first
compression level of the bitmapped XML structure
uses the invertible characteristic of the XML
structure in order to reduce the number of matrices
explicitly encoded in the underlying storage while
the second level of the compression uses the
inclusive characteristics to combine two or more
matrices into a single matrix. The following two
sections formulate the first two compressions while
the third compression process is described then after.
3.3 Invertible-matrix Transformation
Invertible XPath’s axes are those axes which their
XML structural relationships are the inverse of each
other. There are five axis-pairs of this type; the
child, descendent, following, following-sibling and
next axes are the inverse of the parent, ancestor,
preceding, preceding-sibling and previous axes
respectively. The notion of compression in this level
is to encode (consider) only one axis of each axis-
pair in the underlying data storage while the image-
axis can be calculated using simple geometric
transformations on the set (or matrix) representation
of the corresponding XML structure. Thus, the
number of matrices (sets) that need to be encoded in
the underlying data storage is reduced from ten to
five only which in turn halves the amount of storage
space required for the entire XML structure.
As for illustration, the childOf and parentOf
matrices can be algebraically calculated from each
other using the formula childOf[i,j] = parentOf[j,i].
In terms of geometric transformation, the parentOf
matrix can be obtained by rotating the childOf
matrix by 90° clockwise and then reflecting the
matrix on the y-axis. In practice this is simply done
by inverting the first matrix indices to obtain the
entries of the second matrix. The five possible
geometric transformation of XPath’s axes are
formulated in Fig. 6.
3.4 Matrix Clustering
Invertible-matrix transformation were only able to
reduce the number of encoded matrices (XML
structure) from ten to five matrices. Therefore, the
amount of storage space required to store the five
matrices remains big for large XML databases. This
necessitates advances in storage space reduction
which could be achieved by further reduction in the
number of matrices and/or using sophisticated
compression algorithms to store the matrices inside
the computer’s storage media.
In this context, the matrix clustering process
maps the corresponding entries of two or more
matrices to a single entry producing a matrix which
represents the all combined matrices. To do so, two
conditions must apply. Firstly, all combined
matrices must have the same degree of rows and
columns. Secondly, entries of all combined matrices
must have a finite set of values; in other words,
WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies
92

a.
b.
anceOfMdescOf
YY
anceOf
descOf
⎯→⎯⎯→⎯Φ
° '
|90
:
c.
precOfMfollOf
YY
precOf
follOf
⎯→⎯⎯→⎯Φ
° '
|90
:
d.
p
recSibO
f
MfollSibOf
YY
precSibOf
follSibOf
⎯→⎯⎯→⎯Φ
° '
|90
:
e.
prevOfMnextOf
YY
prevOf
nextOf
⎯→⎯⎯→⎯Φ
° '
|90
:
Figure 6: Invertible Transformations of the XML
Structure.
f.
oo
SSdescOfchildOf
descOfchildOf
≤⇒⊆
&
oo
SSanceOfparentOf
anceOfparentOf
≤⇒⊆
g.
oo
SSprecOfprecSibOf
precOfprecSibOf
≤⇒⊆
&
oo
SSfollOffollSibOf
follOffollSibOf
≤⇒⊆
h.
oo
SSprecSibOfprevOf
precSibOfprevOf
≤⇒⊆
&
oo
SSfollSibOfnextOf
follSibOfnextOf
≤⇒⊆
i.
oo
SS
childOfchildOfdescOf
descOfchildOfdescOf
=⇒
=∩
⊕
j.
1−+=⇒
=∩
⊕
ooo
SSS
nextOfchildOf
nextOfchildOfnextOfchildOf
φ
k.
1−+=⇒
=∩
⊕
ooo
SSS
nextOfdescOf
nextOfdescOfnextOfdescOf
φ
A
S° is the sparsity-degree of the matrix A; calculated by
dividing the number of non-zero elements by n
2
⊕ is the addition operation (clustering) of two matrices
Figure 7: More XML structure semantic based on
Matrix/Set representation.
entries must have limited domain of values and the
domains must be identical; e.g. {0, 1} or {a, b, c} for
all matrices. The value of the [i,j]
th
entries from all
matrices are combined somehow to produce the
[i,j]
th
entry in the resulting matrix. For example, if
we have two matrices A and B such that A[i,j] ∈
{0,1} and B[i,j] ∈ {0,1}, then we can use ‘0’, ‘a’,
‘b’ and ‘c’ to respectively map ‘00’, ‘01’, ‘10’ and
‘11’. The resulting matrix, say C, will then have
entries all belong to {0,a,b,c} (i.e. ∀ c
ij
∈ C; C[i,j] ∈
{0,a,b,c}). We call output matrix a Master matrix
and its degree (i.e. dimension) must be the same as
the composing matrices.
In the PACD’s data representation, the above
two conditions are imbedded in the PACD’s storage
specifications (see Section 2.2). So, all matrices
generated are of power ‘n×n’, and the entries of
these matrices have either ‘0’ or ‘1’ values.
Complexity-wise, the cost of the clustering
process itself is determined by the size of the values’
set and the number of clustered matrices. In practice,
the complexity is found low because the process
may cluster a maximum of five matrices with only
two possible values ‘0’ or ‘1’. However, the matrix
clustering process should also consider the trade-off
between the storage space reduction and the
performance issues that incurred by the querying and
updating processes. Due the space limitation, the
discussion of this topic is omitted from this paper.
In general, the clustering process is guided by the
set-based XML semantic listed in Fig. 7. Fig. 8
provides an example of clustering the child and
descendent matrices using a simple-clustering table.
Case 1 Case 2 Case 3
*
Case 4
childOf (A) 0 0 1 1
descOf (B) 0 1 0 1
A&B
‘00’ ‘01’ ‘10’ ‘11’
ƒ(A & B)
0 1 2 3
* Impossible case (see Fig. 6)
&0 &1 &2 &3 &4 &5 … &11
&0000000…0
&1300000…0
&2130000…0
&3130000…0
&4300000…0
&5100030…0
………………………
&11100000...0
924.0=
o
S
childOf
,
854.0=
o
S
descOf
,
854.0=
⊕
o
S
descOfchildOf
Figure 8: A clustering example (childOf ⊕ descOf).
3.5 Sparse-matrix Compression
The maximum compression degree of the first two
levels can reduce the storage requirement of storing
k number of matrices (corresponding to a single
XML tree of size ‘n’ nodes) up to n
2
storage units.
This remains an issue for large XML databases and
multi-document XML databases, where the value of
‘n’ is high with respect to the available system’s
resources. For example, a tree of 10
6
nodes requires
10
12
bytes (≅1000 GB) when each matrix’s entry is
stored using 1-byte storage. Thus, this justify the
need for an additional compression level which acts
on the resulting matrices considering their unique
characteristics; e.g. the sparsity-degree and the
zero’s distribution.
“A matrix is sparse if many of its coefficients are
zero … (and) … Generally, we say that a matrix is
parentOfMchildOf
YY
parentOf
childOf
⎯→⎯⎯→⎯Φ
° '
|90
:
ACOMPRESSEDDATAMODELFORABITMAPPEDXMLSTRUCTURE
93

sparse if there is an advantage in exploiting its
zeros” (Duff et al., 1986). In (George et al., 1993), a
sparse matrix is also defined as the matrix which is
populated mainly with zeros whiles some references
are more specific, limiting the definition to those
matrices with certain amount of 0’s; e.g. 50% of the
entries are 0 as in (Mackay and Neal, 1995).
According to the above, our matrices for
representing the XML structures are considered to
be sparse. This is mainly reflected by the analysis
given in (Al-Badawi, 2010) which shows that the
number of zeros in the childOf and nextOf matrices
reaches n
2
-n, and the numbers of zeros in the descOf
matrix may exceed n
2
-h×n where ‘n’ is the number
of nodes and ‘h’ is the number of levels in the
underlying XML tree. When n goes high, the
number of 0 entries easily exceeds 90% of the total
entries
From a technical point of view, storing matrices
of this size in the computer system is a trade off
between the high storage size and storage
performance (Tarjan and Yao, 1979). For example,
to store a matrix when n=10
6
into two-dimensional
array of type character (one byte stores one
character), we need 10
12
bytes of memory which
may defeat the HW/SW capabilities. One way to
address this issue is using sparse matrix compression
(SMC) techniques to compact the matrix’s storage.
The architecture of any SMC technique depends
on the computation to be performed, the pattern of
the non-zero entries, and even the architecture of the
computer system itself (Duff et al., 1986; Willcock
and Lumsdaine, 2006). Among these three factors,
we are only concerned with the computation
constraints in this stage of our research; having that
achieving optimum storage with good performance
is the main goal of the compression process. The
investigation of other issues is a subject for further
research.
To align the choice of the used SMC with the
cost reduction of the XML querying and updating
operations, PACD categorizes the existing sparse-
matrix techniques into two groups; the first includes
the techniques which do not necessitate any
decompression/recompression process during the
XML querying and updating operations so the
overhead complexity incurred by these processes
will be avoided during the XML querying and
updating. The second category contains those
techniques which defeat the XML operations by the
cost of decompressing/recompressing processes
done to the underlying storage. Detailed discussion
of this aspect plus the empirical proof lays down
outside the scope of this paper due the space
limitation.
4 CONCLUSIONS
To conclude, this paper described the PACD’s DCM
which uses three data compression processes to
compact the XML structures. As introduced in (Al-
Badawi et al., 2009), the XML structures are
theoretically encoded into ten n×n matrices each of
which represents a structural relationship which
corresponds to an XPath’s axis or an extension. Each
structural relationship is encoded into a set of node
pairs where such relationship applies between them.
So, each matrix represents the corresponding
structural relationship between all nodes in the XML
tree.
PACD’s matrices are found in invertible pairs
and inclusive pairs, and are sparse. The first
compression phase uses the first characteristic; that
is each invertible pair is represented by only one
matrix. This process can reduce the number of
matrices from ten to five matrices. The next
compression phase uses the inclusiveness
characteristic; that is two or more matrices are
clustered into a single matrix such that the full
architecture of all composing matrices is preserved
in the clustered matrix. The last compression phase
is based on using one or more sparse-matrix
compression techniques to compact the layout of the
resulting matrix from the first two compressions.
The strength and efficiency of the PACD’s
overall storage is determined by the specification of
the clustering and SMC methods used. A complete
discussion about this topic including the
experimental proof is the subject for further
publications.
REFERENCES
Al-Badawi, M. (2010) ‘A Performance Evaluation of a
New Bitmap-based XML Processing Approach’, PhD
Thesis, University of Sheffield, UK.
Al-Badawi, M., Eaglestone, B., and North, S. (2009)
‘PACD: A Bitmap-based Framework for Processing
XML Data’, In the proceedings of the WebIST’09,
Lisbon, Portugal, pages 66-71.
Berglund, A., Boag, S., Chamberlin, D., Fernández, M.,
Kay, M., Robie, J., and Siméon, J. (2010) XML Path
Language (XPath) 2.0 (2
nd
Ed.), [Online] Avail: http://
www.w3.org/TR/xpath20/ [15/11/2011].
Boag, S., Chamberlin, D., Fernández, M., Florescu, D.,
Robie, J., and Siméon, J. (2010) XQuery 1.0: An XML
Query Language, (2
nd
Ed.) [Online] Avail: http://www
WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies
94

.w3.org/TR/xquery/ [15/11/2011].
Chung, C., Min, J., and Shim, K (2002) ‘APEX: An
Adaptive Path Index for XML Data’, In proceedings
of the 2002 ACM SIGMOD international conference
on Management of data, Madison, Wisconsin, pages
121-132.
Duff, I., Erisman, A., and Reid, J. (1986) Direct Methods
for Sparse Matrices. Oxford University Press, New
York and London.
George, A., Gilbert, J., and Liu, J. (1993) Graph Theory
and Sparse Matrix computation, Volume 56 of the IMA
volumes in Mathematics and its Applications, Volume
56 of Partially Ordered Systems. Springer-Verlag.
Goldman, R., and Widom, J. (1997) ‘DataGuides:
Enabling Query Formulation and Optimaization in
Semistructured Database’, In proceedings of the 23
rd
international conference on VLDB, pages 436-445.
Hammerschmidt, B. (2005) ‘KeyX: Selective Key-
Oriented Indexing in Native XML Databases’, PhD
Thesis Published. in: Dissertations in Database and
Information Systems - Infix, Volume 93, ISBN
1586035894.
Haw, S., and Lee, C. (2009) ‘Extending path summary and
region encoding for efficient structural query
processing in native XML databases’, Journal of
Systems and Software, Volume 82, Issue 6, pages
1025-1035.
He, H., Wang, H., Yang, J., and Yu, P. (2005) ‘Compact
Reachability Labeling for Graph-Structured Data’, In
proceedings of the 14
th
ACM international conference
on Information and knowledge management, Bremen,
Germany, pages 594-601
Mackay, D., and Radford, N. (1995) ‘Good Codes based
on Very Sparse Matrices’, Lecture notes in Computer
Science, Volume 1025/1995, pages 100-111.
McCord, R. (1981) ‘Sizing and Data Distribution for a
Distributed Database Machine’, In proceedings of the
1981 ACM/SIGMOD international conference on
Management of Data, Michigan, USA, pages 198-204.
Milo, T., and Suciu, D. (1999) ‘Index Structures for Path
Expressions’, In proceedings of the 7
th
International
conference on Data Technology, Volume 1540/1998,
Jerusalem, pages 277-295.
O’Neil, P., and O’Neil, E. (2001) ‘Database: Principles,
Programming, and Performance’, Morgan Kaufmann
Publishers, 2
nd
Edition, 2001.
Pettovello, P., and Fotouhi, F. (2006) ‘MTree: An XML
XPath Graph Index’, ACM/Sym. on Applied
computing, Dijon, France, pages 474-481.
Sun, J., Xie, Y., Zhang, H., and Faloutsos, C. (2008) ‘Less
is More: Sparse Graph Mining with Compact Matrix
Decomposition’, Journal of Statistical Analysis and
Data Mining, Volume 1, Issue 1, pages 6-22.
Tarjan, R., and Yao, A. (1979) ‘Storing a Sparse Table’,
Journal of Communications of theACM, Volume 22,
Issue 11, pages 606-611.
Wang, H., He, H., Yang, J., Yu, P., and J Yu. (2006) ‘Dual
Labeling: Answering Graph Reachability Queries in
Constant Time’, In the proceedings of the
International conference of Data Engineering, pages
75-86.
Willcock, J., and Lumsdaine, A. (2006) ‘Accelerating
Sparse Matrix Computations via Data Compression’,
In proceedings of the 20
th
international conference on
Supercomputing, Queensland, Australia, pages 307-
316.
ACOMPRESSEDDATAMODELFORABITMAPPEDXMLSTRUCTURE
95
