How to Use an Adaptive High-gain Observer in Diagnosis Problems
Fr´ed´eric Lafont
1,2
, Jean-Franc¸ois Balmat
1
, Nathalie Pessel
1,2
and Jean-Paul Gauthier
1,2
1
Universit´e du Sud-Toulon-Var, LSIS, UMR CNRS 7296, B.P 20132, 83957 La Garde Cedex, France
2
Institut Universitaire de Technologie de Toulon, B.P 20132, 83957 La Garde Cedex, France
Keywords:
Observer, Diagnosis, Sensor.
Abstract:
This paper explains how to use an adaptive High-Gain observer in sensor diagnosis problems. This type of
observer allows to switch between a classical Extended Kalman Filter and High-Gain observer according to
an innovation function. Combined with a standard technique of residual generation, this approach is very
efficient to determine fault occurence in the non-linear dynamical systems. We present the obtained results on
a wastewater treatment system.
1 INTRODUCTION
Nowadays, systems are more and more automated in
order to reduce the human intervention. So, these sys-
tems are composed of sensors and actuators. There-
fore, it involves to define a structure enable to detect
a sensor fault or a failing actuator. The aim of such
equipment is the diagnosis of failure to avoid the eco-
nomic losses and/or the environmental risks.
The present work deals the sensor diagnosis with
an observer for non-linear dynamical systems ap-
plied to a wastewater treatment system. There is a
lot of works on the synthesis of non-linear observers
for (bio)chemical processes (Alcaraz-Gonzalez et al.,
2002; Assis and Filho, 2000; Dochain, 2008; Meth-
nani et al., 2011; Nejjari et al., 2008; Sotomayor et al.,
2002). In this study, we choose an adaptive high-
gain observer, developed already as software sensor
(Boizot et al., 2010; Lafont et al., 2011), to solve a
sensor diagnosis problem. Transition from High-Gain
(HG) mode to Extended Kalman Filter (EKF) mode
is performed via an adaptation procedure based upon
the level of innovation. In the context of large transi-
tions, the HG observer guarantees theoretical conver-
gence with arbitrary rate, under certain observability
assumptions. For small enough error of initial esti-
mation, classical EKF is more or less optimal w.r.t.
noise.
Usually a changing coordinates is necessary in or-
der to obtain an observability canonical form. In some
cases, this change of coordinates is very complicated.
To avoid this step, we write our observer in the natural
coordinates. However, the counterpart of this choice
is that the Riccati equation of the Kalman filter has
not the standard form (Lafont et al., 2011).
A such observer is “robust” compared with ini-
tial conditions and measurement noises. Although the
generation of residues is standard, we show the capa-
bility of adaptive HG-EKF observer to detect a sensor
fault.
Section 2 summarizes sensor diagnosis problems
and observer-based residual generation. In Section 3,
we recall the structure of the adaptive high-gain ob-
server, which is the multi-output version developed in
the paper (Boizot et al., 2010). Also, the crucial con-
cept of innovation, which is used in order to switch
between the EKF and HG-EKF modes, is presented.
Section 4 is devoted to the application: A wastewater
treatment plant. Finally, in Section 5, we show simu-
lation results.
2 SENSOR DIAGNOSIS AND
OBSERVER
2.1 Sensor Diagnosis
We are interested at the problem of the bias and the
drift faults. These two faults are the most common
and the most repetitive.
An output with a bias fault is defined by:
y
i
= y
r
+ b, (1)
with y
i
is the measured output, y
r
the real output and
b the constant offset value.
185
Lafont F., Balmat J., Pessel N. and Gauthier J..
How to Use an Adaptive High-gain Observer in Diagnosis Problems.
DOI: 10.5220/0003984501850190
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 185-190
ISBN: 978-989-8565-22-8
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

An output with a drift fault is defined by:
y
i
= y
r
+ d(t), (2)
with y
i
is the measured output, y
r
the real output and
d(t) the time varying offset factor. d(t) can be rep-
resented by the function: d(t) = a t + b with a and b
two constant terms.
2.2 Observer-based Residual
Generation
The main problem for the diagnosis based on ob-
servers is to find the residues. They are neglectable
in the absence of fault and significantly affected when
some faults occur. One difficulty is to make the robust
observer w.r.t. disturbances which are no faults.
So, a non-linear system can be written:
dx
dt
= f (x, u),
y = h(x) = Cx,
(3)
where x is the state vector, y the measured outputs
and u the control variables.
The corresponding observer is defined by:
d ˆx
dt
= g( ˆx,u),
ˆy =
ˆ
Cˆx,
(4)
The output estimation error is used to residual
generation. The residual is analysed to determine
fault occurence. We apply a standard method:
r
i
= |y
i
− ˆy
i
|. (5)
The output has a fault if r
i
> δ
i
. For each out-
put, we simulate off-line in nominal operating (with-
out fault) to determine the threshold level δ
i
. Then,
the method is applied on-line.
3 SYSTEMS UNDER
CONSIDERATION AND
OBSERVER EQUATIONS
3.1 The Observability Canonical Form
We consider a smooth non-linear system of the form
(3) which is mapped by a diffeomorphism ψ into the
following system:
dξ
dt
= F (ξ, u) = A(t)ξ + b(ξ, u),
y = Cξ,
(6)
where ξ ∈ R
n
is the state vector in observable co-
ordinates (n the system order), where u are the control
variables belonging to a certain bounded subset of R
p
(p the number of the control variables) and the output
y ∈ R
d
0
(d
0
the number of the outputs).
The matrices A(t), C and the vector b(ξ, u) have
a following form (all details can be found in (Boizot
et al., 2010)):
A(t) =









0 a
2
(t) 0 ··· 0
0 0 a
3
(t)
.
.
.
.
.
.
.
.
. ·· ·
.
.
.
.
.
.
0
.
.
. ·· · ·· · 0 a
k
(t)
0 0 ·· · ·· · 0









,
C = (a
1
(t), 0, ··· , 0) = (Id, 0, ·· · , 0),
(7)
where Id is an identity matrix of order d
0
.
b(ξ, u) =




b
1
(ξ
1
, u)
b
2
(ξ
1
, ξ
2
, u)
.
.
.
b
n
(ξ
1
, · ·· , ξ
k
, u)




. (8)
The state vector ξ(t) is assumed to have a “block”
structure ξ =

ξ
′
1
ξ
′
2
·· · ξ
′
k

′
, where ξ
i
∈ R
d
i
−1
(d
i
the
size of i+ 1
th
“block”) with d
0
≥ d
1
≥ · · · ≥ d
k−1
. The
matrices a
i
(t) have dimension d
i−1
×d
i
and belong to
a compact subset K
i
of the set of d
i−1
× d
i
matrices of
maximum rank d
i
.
The f (x, u), a
i
(t) and b
i
(ξ, u) are assumed
smooth w.r.t. ξ, u and t. The b
i
depend on ξ in a
“block” triangular way and are compactly supported.
3.2 Observer Structure
Let Q (n × n) , R (d
0
× d
0
) be symmetric positive
definite matrices. Let θ be the high-gain parameter,
θ ≥ 1. For θ = 1 the observer will just be an ordinary
EKF.
Set ∆ = BD

1,
1
θ
, · ·· ,
1
θ
k−1

, the block diagonal
matrix with diagonal blocks Id
d
0
,
1
θ
Id
d
1
, · ·· . Set Q
θ
=
θ∆
−1
Q∆
−1
, R
θ
= θ
−1
R.
The equations of the system in observable coordi-
nates are:
dξ
dt
= Tψ

ψ
−1
(ξ)

f

ψ
−1
(ξ), u

,
dξ
dt
= F (ξ, u) .
(9)
The equations for the HG-EKF in the observable
coordinates are:
d
ˆ
ξ
dt
= F(
ˆ
ξ, u) + PC
′
R
−1
θ
(y−C
ˆ
ξ), (10)
dP
dt
= TF(
ˆ
ξ, u) P+ P TF(
ˆ
ξ, u)
′
+ Q
θ
−PC
′
R
−1
θ
CP.
(11)
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
186

In the natural coordinates we have ˆx = ψ
−1
(
ˆ
ξ) =
Φ( ˆx), where ˆx denotes the estimate of x. As shown in
(Lafont et al., 2011), the equations for the HG-EKF
become:
d ˆx
dt
= f( ˆx, u) + pC
′
( ˆx, u)R
−1
θ
(y− h( ˆx)), (12)
dp
dt
= T f ( ˆx, u)p+ pT f( ˆx, u)
′
+ q
θ
( ˆx)
−pC
′
R
−1
θ
Cp
+Tψ( ˆx)
−1
D
2
ψ( ˆx)
n
pC
′
R
−1
θ
(h( ˆx) − y)
o
p
+pD
2
ψ( ˆx)
n
pC
′
R
−1
θ
(h( ˆx) − y)
o
′

Tψ( ˆx)
−1

′
,
(13)
where
p = TΦ

ˆ
ξ

P TΦ

ˆ
ξ

′
(14)
and
q
θ
( ˆx) = (Tψ( ˆx))
−1
Q
θ

(Tψ( ˆx))
−1

′
. (15)
TF denotes the tangent mapping to the mapping
F : x → F (x), R
n
→ R
n
i.e. its Jacobian matrix in co-
ordinates. Accordingly T
2
F denotes the double tan-
gent, a skew-symmetric bilinear mapping, R
n
-valued,
and for any u ∈ R
n
we define the matrix D
2
F (x){u}
by T
2
F (u, v) = D
2
F (x){u} · v.
3.3 Innovation
The function In
d
, introduced below, is called the inno-
vation. This function reflects the quality measurement
of the estimation error on a small moving time inter-
val of size d. The strategy is to adapt the High-gain
parameter θ according to In
d
. Due to the observabil-
ity properties of our system, if the ˆy is far from y then
θ will increase to High-gain mode. Contrarily, if ˆy
is close to y, the innovation will be small and θ will
decrease to 1 (Kalman filtering mode). For this, the
variable θ will be subject to the differential equation
(19) defined just below.
Let F
o
(θ) be defined as follows:
F
o
(θ) =

1
∆T
θ
2
if θ ≤ θ
1
,
1
∆T
(θ− 2θ
1
)
2
if θ > θ
1
,
(16)
where θ
1
=
1
2
θ
max
and ∆T small enough is a constant.
The value θ
max
depends of the studied system and is
obtained by an heuristic approach. It is bounded and
the observer remains stable.
The innovation In
d
(t), with forgetting horizon d,
is:
In
d
(t) =
Z
d
t− d
ky(τ) − ˆy(τ)k
2
dτ, (17)
where ˆy(τ) is the prediction from the initial state
ˆx(t − d).
Let us define
F (θ, In
d
) = µ(In
d
)F
o
(θ) + (1− µ(In
d
))λ(1− θ),
(18)
for a λ > 0 and with µ(In
d
) a sigmoid function,
µ : ]−∞;+∞[→] 0;1[ , In
d
→
1
1+e
−β·
(
In
d
−m
)
. The equa-
tion for the HG parameter θ is:
˙
θ = F (θ, In
d
). (19)
4 APPLICATION
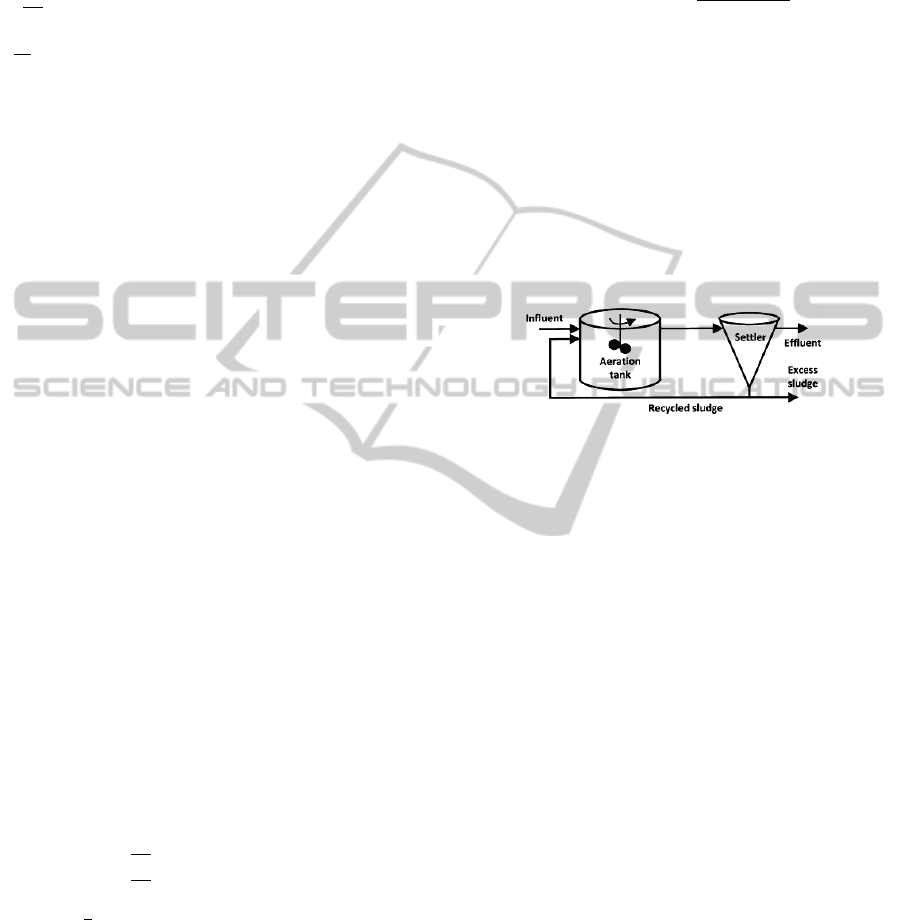
The process under consideration is a real small-size
wastewater treatment plant (WWTP) composed of a
unique aeration tank equipped with surface aerators
which provide oxygen and mix the influent wastewa-
ter with biomass (Figure 1).
Figure 1: Wastewater treatment plant.
The model used is based upon the Activated
Sludge Model N
1
(ASM 1) (Henze et al., 1987). Then
the biodegradation model consists of 12 state vari-
ables (Table 1). Actually, we consider only biodegra-
dation.
The state variables describing the total alkalinity
being not included. The values of stoichiometric and
kinetic parameters, as well as the influent concentra-
tions can be found in (Lafont et al., 2011).
The complete set of equations and influent con-
ditions can be found on the International Water As-
sociation task group on benchmarking of control
strategies for wastewater treatment plants website
(http://www.benchmarkwwtp.org/, 2011).
The model is of the form ˙x = f (x, u), where the
control u consists of the state u
b
of the turbines and
the value Q
in
of the influent average flow. The input
u
b
in (20) is a binary sequence switching between 0
and 1 and representing the state of turbines (off/on)
that aerate the plant. We make here the reasonable as-
sumptions of three measurements: S
O
, S
NO
and S
NH
.
Although the WWTP with these three outputs is ob-
servable, it is too complicated for our purpose. We
use a simplified model of lower dimension that has
been developped in (Chachuat, 2001).
4.1 The Reduced Model
The author proceeds as follow:
HowtoUseanAdaptiveHigh-gainObserverinDiagnosisProblems
187

Table 1: List of variables.
Definition Notation
1. Soluble inert organic matter S
I
2. Readily biodegradable substrate S
S
3. Particulate inert organic matter X
I
4. Slowly biodegradable substrate X
S
5. Active heterotrophic biomass X
B,H
6. Active autotrophic biomass X
B,A
7. Particulate products arising from biomass decay X
P
8. Oxygen S
O
9. Nitrate and nitrite nitrogen S
NO
10. NH
+
4
+ NH
3
nitrogen S
NH
11. Soluble biodegradable organic nitrogen S
ND
12. Particulate biodegradable organic nitrogen X
ND
- A single organic compound, denoted X
DCO
(DCO for “chemical oxygen demand”), is formed
by adding soluble and particulate organic compound
concentrations X
DCO
= S
S
+ X
S
,
- It is considered that the dynamics of X
BH
, X
BA
and X
ND
are slow w.r.t. the others.
By removing the three unobservable variables X
P
,
X
I
and S
I
, we obtain a simplified model with 5 state
variables S
O
, S
NO
, S
NH
, X
DCO
and S
ND
. The three
variables S
O
, S
NO
and S
NH
are observables. All these
simplifications provide the following reduced model:
˙
S
O
=
Q
in
V

S
in
O
− S
O

+ α
1
X
DCO
K
DCO
+X
DCO
·
S
O
K
O,H
+S
O
+ er
1
(y) + u
b
· k
L
a·

S
max
O
− S
O

(20)
˙
S
NO
=
Q
in
V

S
in
NO
− S
NO

+ α
3
X
DCO
K
DCO
+X
DCO
·
K
O,H
K
O,H
+S
O
S
NO
K
NO
+S
NO
+ er
2
(y)
(21)
˙
S
NH
=
Q
in
V

S
in
NH
− S
NH

+ α
5
X
DCO
K
DCO
+X
DCO
·

S
O
K
O,H
+S
O
+ η
NO,g
K
O,H
K
O,H
+S
O
S
NO
K
NO
+S
NO

+ er
3
(y) + α
6
S
ND
(22)
˙
X
DCO
=
Q
in
V

X
in
DCO
−
K
S
K
DCO
X
DCO

+α
7
X
DCO
K
DCO
+X
DCO

S
O
K
O,H
+S
O
+η
NO,g
K
O,H
K
O,H
+S
O
S
NO
K
NO
+S
NO

+ α
8
(23)
˙
S
ND
=
Q
in
V

S
in
ND
− S
ND

− α
6
S
ND
+ α
9
·
X
DCO
K
ND
+X
DCO

S
O
K
O,H
+S
O
+ η
NO,h
K
O,H
K
O,H
+S
O
·
S
NO
K
NO
+S
NO

(24)
K
DCO
= K
S
X
DCO
S
S
K
ND
= K
X
X
DCO
X
S
X
B,H
(25)
er
1
(y) = α
2
S
NH
K
NH,A
+S
NH
S
O
K
O,A
+S
O
er
2
(y) = α
4
S
NH
K
NH,A
+S
NH
S
O
K
O,A
+S
O
er
3
(y) = −α
4
S
NH
K
NH,A
+S
NH
S
O
K
O,A
+S
O
(26)
The constant k
L
a is the oxygen transfer coef-
ficient

k
L
a = 10 h
−1

and S
max
O
is the dissolved
oxygen saturation concentration

S
max
O
= 8 mgl
−1

.
The volume of the aeration tank (V) is equal to
6000 m
3
. The settler is a cylindrical tank where
the solids are either recirculated to the aeration tank

Q
rs
= 18446 m
3
day
−1

or extracted from the system

Q
w
= 385 m
3
day
−1

. The parameter values α
1
, α
2
,
α
3
, α
4
, α
5
, α
6
, α
7
, α
8
, α
9
, K
ND
and K
DCO
are given
in Table 2.
4.2 Change of Variables
We apply the developed observer to a simplified
model (five states, three outputs). The change of vari-
ables Ψ which relates natural coordinates to observer
coordinates is trivial. It consists of setting just :
]
X
DCO
=
X
DCO
K
DCO
+ X
DCO
. (27)
The state vector x = (S
O
S
NO
S
NH
X
DCO
S
ND
)
′
is
changed for ξ =

S
O
S
NO
S
NH
]
X
DCO
S
ND

′
, therefore
our system is almost naturally in observable coordi-
nates. The inverse Jacobian is trivial to compute.
The choice of parameters for the adaptation of in-
novation is presented in Table 3.
5 RESULTS
Simulations with the perturbed outputs are carried
out by an additive Orstein-Uhlenbeck process. The
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
188

Table 2: Constant coefficients.
Coefficient α
1
α
2
α
3
α
4
α
5
α
6
α
7
α
8
α
9
K
DCO
K
ND
Value - 5892 - 875 - 1648 191 - 957 150 - 17855 830 561 574 296
Table 3: Parameters for the adaptation.
Parameter value
θ
max
300
β 1664
π
e
m 1
∆T 0.01
λ 200
δ 0.01
d 0.1
alternative control u
b
has been chosen: “On” dur-
ing 15 minutes and “Off” during 5 minutes. The
simulations cover 14 days and the value of the in-
put flow rate Q
in
come from the benchmark file
(http://www.benchmarkwwtp.org/, 2011). We have
three files: One for the dry weather, one for the storm
weather and one for the rain file.
To evaluate the performances of our observer we
have compared an ordinary EKF with our adaptive
HG-EKF presented in (Lafont et al., 2011). Consider-
ing the obtained results for this system, we propose to
use this adaptive HG-EKF observer for the diagnosis.
5.1 Threshold Level for each Output
For each output, we simulate the three files, without
fault, to determine the threshold level δ
i
(Table 4).
Table 4: Threshold level.
File/Output S
O
S
NO
S
NH
Dry 0.2505 0.9453 0.2466
Rain 0.2440 0.9306 0.2247
Storm 0.2576 0.9605 0.2200
We have selected one threshold level by output.
For S
O
, the taken threshold is 0.3, for S
NO
, 1.0 and for
S
NH
, 0.3. These levels must be valid for whatever file.
5.2 Faults
The bias and the drift faults are simulated. The bias
value is equal to 1.5 and 2. The drift fault is simulated
with two curve slopes: (t −t
f
) and 2∗(t−t
f
), t
f
is the
fault time and t is the simulation time.
Results are presented in Tables 5 and 6 where t
d
is
the detection time. Only the results for the fault time
equal to 3 with the dry file are presented in Table 5.
Indeed, the three files have the same seven first days.
Moreover, Tables 5 and 6 present two interesting re-
sults:
- Whatever the fault time t
f
, the various faults are
detected,
- If the fault is more important, it is detected
quickly.
6 CONCLUSIONS AND FUTURE
WORKS
6.1 Conclusions
We have shown that an adaptive HG-EKF observer
is efficient to detect sensor faults such as bias and
drift. The proposed method imposes to determine the
threshold levels with no fault. Thanks to the “robust-
ness” (compared with noise and initial conditions) of
this observer and thethreshold choice for the residues,
the adaptive HG-EKF observer is an interesting ap-
proach for the sensor diagnosis. Moreover, the resid-
ual generation is very easy.
To improve the method, we can work with the
eigenvalues of the matrix p. The calculation of the
trace permits to give a confirmation:
Trace(p) =
n
∑
i=1
V
i
, (28)
where V
i
are the eigenvalues. When there is a sensor
fault, the trace has an abrupt change (Figure 2). This
result is a complementary information but it is not sat-
isfactory, because if the value Q
in
increases, the trace
becomes very big and the algorithm indicates a false
alarm.
2.97 2.98 2.99 3 3.01 3.02 3.03
0
1
2
3
x 10
10
Day
Trace
Figure 2: Trace with a fault at t
d
= 3 days.
6.2 Future Works
To improve this method, we can use the trace prop-
erties. The trace value is compared with the influ-
HowtoUseanAdaptiveHigh-gainObserverinDiagnosisProblems
189

Table 5: Faults detection for the dry file.
Fault/Sensor S
O
S
NO
S
NH
t
d
t
d
t
d
Bias +1.5, t
f
= 3 3.0002 3.012 3.0004
Bias +1.5, t
f
= 12 12.0001 12.158 12.0004
Bias +2, t
f
= 3 3.0001 3.009 3.0003
Bias +2, t
f
= 12 12.0001 12.028 12.0002
Drift (t − t
f
), t
f
= 3 3.222 4.455 3.215
Drift (t − t
f
), t
f
= 12 12.150 12.739 12.197
Drift 2∗ (t −t
f
), t
f
= 3 3.092 3.539 3.090
Drift 2∗ (t −t
f
), t
f
= 12 12.067 12.959 12.115
Table 6: Faults detection for the rain and storm file.
Fault/Sensor S
O
S
NO
S
NH
File
t
d
t
d
t
d
Bias +1.5, t
f
= 12 12.0001 12.189 12.0004
Bias +2, t
f
= 12 12.0001 12.013 12.0003 Rain
Drift (t −t
f
), t
f
= 12 12.176 13.528 12.189
Drift 2∗ (t −t
f
), t
f
= 12 12.086 12.933 12.084
Bias +1.5, t
f
= 12 12.0001 12.201 12.0005
Bias +2, t
f
= 12 12.0001 12.012 12.0003 Storm
Drift (t −t
f
), t
f
= 12 12.175 13.813 12.203
Drift 2∗ (t −t
f
), t
f
= 12 12.089 12.941 12.084
ent flow rate by developing a “black box” (neural net-
works for example) which select the peak level to no-
tify a fault.
REFERENCES
Alcaraz-Gonzalez, V., Harmand, J., Rapaport, A., Steyer, J.-
P., Gonzalez-Alvarez, V., and Pelayo-Ortiz, C. (2002).
Software sensors for highly uncertain wwtps : a new
approach based on interval observers. Water Research,
36:2515–2524.
Assis, A. and Filho, R. (2000). Soft sensors development
for on-line bioreactor state estimation. Computers and
Chemical Engineering, 24:1099–1103.
Boizot, N., Busvelle, E., and Gauthier, J.-P. (2010). An
adaptive high-gain observer for nonlinear systems.
Automatica, 469:1483–1488.
Chachuat, B. (2001). Methodology of dynamic optimisa-
tion and optimal control of small-size activated sludge
wastewater treatment plants. PhD, Institut National
Polytechnique de Lorraine, Nancy.
Dochain, D. (2008). Bioprocess control. volume ISBN
9781848210257. ISTE.
Henze, M., Grady, C., Gujer, W., Marais, G., and Matsuo, T.
(1987). Activated sludge model n1. In IAWQ, editor,
Technical Report 1. London.
http://www.benchmarkwwtp.org/ (2011).
Lafont, F., Busvelle, E., and Gauthier, J.-P. (2011). An
adaptive high-gain observer for wastewater treatment
systems. Journal of Process Control, 21:893–900.
Methnani, S., Gauthier, J.-P., and Lafont, F. (2011). Sen-
sor fault reconstruction and observability for unknown
inputs, with an application to wastewater treatment
plants. International Journal of Control, 84.4:822–
833.
Nejjari, F., Puig, V., Giancristofaro, L., and Koehler, S.
(July 6-11, 2008). Extended luenberger observer-
based fault detection for an activated sludge process.
Proceedings of the 17th World Congress The Interna-
tional Federation of Automatic Control, Seoul, Korea,
pages 9725–9730.
Sotomayor, O., Park, S., and Garcia, C. (2002). Software
sensor for on-line estimation of the microbial activ-
ity in activated sludge systems. ISA Transactions,
41:127–143.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
190