
Differential Evolution in Parameter Identification
Fuel Cell as an Example
Aki Sorsa, Anssi Koskenniemi and Kauko Leiviskä
University of Oulu, Control Engineering Laboratory, P.O.Box 4300, FIN- 90014, Oulu, Finland
Keywords: Differential Evolution, Identification, Nonlinear Model, Fuel Cell.
Abstract: Evolutionary algorithms are optimization methods and their basic idea lies in biological evolution. They suit
well for large and complex optimization problems. In this study, differential evolution is applied for
identifying the parameters of the nonlinear fuel cell model. Different versions of the algorithm are used to
compare the genetic operators they use. One problem with the studied algorithms is also in defining the
internal parameters that regulate the development of the population. In this paper, entropy is used for
defining the population size and other parameters are tuned using recommendations from the literature and
by trial-and-error. The results show that DE/rand-to-best/1/bin is the most suitable algorithm for the studied
problem. Selection of the crossover operator has no considerable effect on the results. The results also show
that the studied identification problem has a lot of local minima that are very close to each other that makes
the optimization problem even more challenging.
1 INTRODUCTION
Parameter identification typically takes advantage of
numerical methods, such as gradient algorithms.
These methods usually search near the initial guess
and therefore are prone to get trapped into local
optima. In such a case, the optimal parameter values
are not found and the model performance
deteriorates. It is possible to try multiple initial
guesses and then select the best solution or to use
other methods such as evolutionary algorithms.
(Ikonen and Najim, 2002).
Evolutionary algorithms are an interesting
subgroup of search and optimization methods which
have become more popular with advanced computer
technology. The basic idea of evolutionary
algorithms lies in imitating biological evolution
which has shown its competence during millions of
years. Evolutionary algorithms suit particularly well
for large and complex optimization problems. They
are typically based on the population of possible
solutions which is then evolved to better solutions to
end up with the optimal one. The evolution of the
population is regulated by operators derived from
the nature: selection, crossover and mutation. The
possible solutions are assessed through an objective
function. The better solutions have a higher
probability to reproduce and thus their properties are
enriched in later generations (Sarker et al., 2003).
Evolutionary algorithms are more likely to find
the global optimum than the traditional algorithms.
They search the optimum from multiple directions
simultaneously and they also allow (in some cases)
the search to proceed to a direction leading to worse
solutions. Therefore evolutionary algorithms are
likely to escape local optima. Another benefit of
evolutionary algorithms is that they do not require
prior knowledge about the optimization problem.
(Storn and Price, 1997; Chipperdale, 1997).
The disadvantage of evolutionary algorithms is
that it is never certain that the search converges to
the global optimum. One possibility is to use them in
finding promising regions in the search space and
then continue with traditional methods. For such
tasks, different kinds of hybrid algorithms have been
proposed. For example, genetic algorithms (GA)
were used to find the initial guesses for a Nelder-
Mead optimization routine in (Wolf and Moros,
1997. GA was used similarly in (Katare et al., 2004)
except that a modified Levenberg-Marquardt
optimization method was applied. A third type of
hybrid algorithm is presented in (Mo et al., 2006)
using the Nelder-Mead search as a part of the
objective function.
In this paper, Differential Evolution (DE)
algorithms are used in identifying a nonlinear
40
Sorsa A., Koskenniemi A. and Leiviskä K..
Differential Evolution in Parameter Identification - Fuel Cell as an Example.
DOI: 10.5220/0004013300400049
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 40-49
ISBN: 978-989-8565-21-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

process model for a proton exchange membrane
(PEM) fuel cell (see also Sorsa et al., 2010,
Chakraborty et al., 2012). In the PEM fuel cell,
electrodes are separated by a solid polymer-
electrolyte-membrane structure through which only
protons can permeate. The behaviour of the fuel cell
is influenced by the prevailing conditions such as
temperature and pressure so in addition to an
electro-chemical model, mass and energy balances
are needed. PEM fuel cells have been found suitable
for both residential and mobile applications because
of operation at relatively low temperatures,
relatively high power density and easy maintenance.
The paper proceeds as follows: Chapter 2
introduces the PEM fuel cell and its model together
with parameters to be identified. Chapter 3 presents
the basics of Differential Evolution, specifies the DE
algorithms tested in this study and tells about their
tuning. Chapter 4 discusses on the results and
compares the performance of chosen algorithms.
Chapter 5 is a short conclusion concerning with the
main results.
2 PROCESS AND PARAMETER
DESCRIPTION
2.1 Pem Fuel Cell
Clean energy production has become very topical
due to environmental problems such as acid rains,
CO
2
emissions and reduction in air quality. Fuel
cells are one of the most promising alternatives
which convert chemical energy to electricity and
overcome these problems. PEM fuel cells include an
anode and a cathode together with a membrane
separating them. The membrane allows only protons
to permeate it. In its simplest form, the fuel cell uses
only hydrogen and oxygen even though the latter
one can also be substituted with air. Hydrogen gas is
fed to the anode where it is oxidized according to the
first reaction in Table 1. The released electrons are
transported to the cathode through a conducting
element. H
+
-ions migrate through the membrane and
also end up in the cathode where they are reduced
according to the second reaction. For the reduction
reaction, oxygen is provided to the cathode. When
hydrogen and oxygen react, only water is produced.
The oxidation and reduction reactions together with
the overall reaction are given in Table 1. (Mo et al.,
2006)
Table 1: Chemical reactions occurring in a PEM fuel cell
(Mo et al., 2006).
Oxidation of H
2
(anode) 2H
2
→ 4H
+
+ 4e
-
Reduction of H+ (cathode) O
2
+ 4H
+
+ 4e
-
→ 2H
2
O
Overall reaction 2H
2
+ O
2
→ 2H
2
O
The models proposed for PEM fuel cells
typically include mass and energy balances
combined with the electrochemical part describing
the relation between the outlet voltage and current.
Only the electrochemical part is studied here and the
model given earlier in (Ohenoja and Leiviskä, 2010)
is used
{
()
}
{}
()
{}
{}
max
3
50,5
22
12 3 4 2
1,229 0,85 10 ( 298,15)
4,3085 10 ln
ln( ) ln( )
ln(1 )
Nernst Act ohm conc
HO
O
i
i
MC
VE V V V
T
TPP
TTi TC
iR R B
ξξ ξ ξ
−
−
=
−− −
=−⋅ −
+⋅
−+ + +
−+− −
(1)
Above, E
Nernst
is the internal potential, V
act
, V
ohm
and V
conc
describe different losses, T is the
temperature, P refers to the partial pressure of the
component in question, C is the concentration, i is
the current, and i
max
is the maximum current value
where fuel is used and applied at its maximum rate.
Figure 1 presents a typical current-voltage curve
(polarization curve) of a fuel cell operating at 70 °C
and standard pressure. The figure shows that even
with no external load the theoretical maximum
voltage is not reached. Furthermore, very low
current densities lead to the cell voltage
experiencing a significant voltage drop which then
settles to a gentler and almost linear drop with
increasing current densities. The voltage drop then
increases again with higher values of the current
density. (Larminie and Dicks, 2003)
For identifying the model parameters,
experimental data is available in (Mo et al., 2006).
That data is obtained from a 250 W PEM fuel cell.
0
0,2
0,4
0,6
0,8
1
1,2
0 200 400 600 800 1000
Cellvoltage [V]
Currentdensity[mAcm
‐2
]
"Noloss" voltageof1,2V
Thetheoretic almaximum voltageis notreached
Rapidinitialvoltage drop
Almostlinearvoltage drop
Increasedvoltagedrop
athighercurrents
Figure 1: A typical current-voltage curve for a fuel cell
operating at low temperature and standard pressure.
Redrawn based on (Larminie and Dicks, 2003).
DifferentialEvolutioninParameterIdentification-FuelCellasanExample
41

The used data includes four sets of current and
voltage measurements. Each set is obtained in
different operating conditions and includes 15 data
points.
The data sets are visualized in Figure 2. Same
data sets have been earlier used in (Mo et al., 2006,
Ohenoja and Leiviskä, 2010). Two of the data sets (1
and 2) are used for model identification while the
remaining two sets (3 and 4) are used for model
validation. The objective function is the sum of the
squared error of prediction (SSEP). For one data set,
the objective function is given by
()
∑
=
−=
N
i
y
ˆ
yJ
1
2
(2)
where N is the number of data points in the set. The
overall objective function is obtained by summing
the SSEPs of the data sets in question
2.2 Parameters to be Identified
The parameters to be identified are the seven
parameters in the PEM fuel cell model in (1). The
parameters are the empirical coefficients ξ
1
, ξ
2
, ξ
3
and ξ
4
, B and λ and the overall resistance R
c
. The
model is simplified by assuming the maximum
current density (i
max
) and the membrane resistance
(R
M
) constant even though they are known to depend
on the reaction conditions (Mo et al., 2006). Because
of these assumptions, a small prediction error is
introduced. Further simplifications are made by
assuming ξ
2
as an identified parameter even though
it is stated in (Mann et al., 2000) that ξ
2
should be
considered as a function of the electrode effective
area and the dissolved hydrogen concentration.
The search space for the parameters used in this
paper is given in Table 2.
3 DIFFERENTIAL EVOLUTION
3.1 Basics of DE Algorithms
Differential Evolution was introduced in (Storn and
Price, 1995). The algorithm is simple, easy to use
and converges well (Zaharie, 2002). Among
evolutionary algorithms, it is closest to GA. The
fundamental difference is the basic principle of the
mutation operator. While random changes are
produced in GA, the differences between
chromosomes are arithmetically combined in DE
(Feoktistov and Janaqi, 2004). When compared to
GA, DE has fewer tuneable parameters. For
example, the simplest form of DE has only three
parameters: the mutation coefficient F, crossing
coefficient CR and the population size NP (Storn
and Price, 1995).
In DE, simple arithmetic operators are combined
to traditional genetic operations (crossover, mutation
and selection). Because the size of the step to be
taken towards the optimum changes as the algorithm
proceeds, the mutation operator must be adaptive.
The differences between the chromosomes indicate
an appropriate step size. When the variance among
the population members increases or decreases so
does the step size in DE. (Bergey and Ragsdale,
2005) To avoid premature convergence, there must
be enough diversity in the population (Zaharie,
2002)
DE utilizes the differences between the
population members. The mutant vector is created
by selecting e.g. three chromosomes from the
population. Two of these are used to create the
difference vector which is then multiplied by the
mutation coefficient F and added to the base vector
of mutation (the third chromosome). The mutant
vector is given by (Price et al., 2005)
)XX(FXV
G,rG,rG,rG,i
321
−
+
=
(3)
Above, V
i,G
is the mutant vector,
G,r
X
1
is the
base vector for mutation and
G,r
X
2
and
G,r
X
3
are
the random vectors for creating the difference
vector. The next step in DE is to produce the trial
vector by the crossover of the mutant and target
(X
i,G
) vectors. In binomial crossover, the resulting
element j in the trial vector is (Storn and Price,
1997)
(
)()
() ()
⎩
⎨
⎧
≠>
=≤
=
irnbrjorCRjrandbif,x
irnbrjorCRjrandbif,v
u
G,j,i
G,j,i
G,j,i
(4)
Above, randb(j) is a uniformly distributed
random number between 0 and 1, rnbr(i) is a random
integer between 1 and D, where D is the number of
identified model parameters and thus the length of
Table 2: The search space used in parameter identification.
ξ
1
ξ
2
[⋅10
-3
] ξ
3
[
⋅
10
-4
] ξ
4
[
⋅
10
-5
] B
λ
R
c
[
⋅
10
-3
]
Lower limit -1 0 -2 7 0.016 9 0
Upper limit 0 5 -1 13 0.5 23 1
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
42

the chromosome. To guarantee the diversity, one of
the elements in the trial vector must be taken from
the mutant vector. Therefore, the mutation
probability, pm, does not equal to CR.
Through crossover, the trial vector (U
i,G
) is
obtained and compared to the target vector in the
selection step. The selection method is the
tournament selection with two candidates. In other
words, the fitter vector is moved to the new
population according to (Price et al., 2005)
(
)()
⎩
⎨
⎧
≤
=
+
otherwise,X
XJUJif,U
U
G,i
G,iG,iG,i
G,i 1
(5)
Above, J is the objective function. The selection
given in (5) guarantees that all the chromosomes in
the new population are equal or better compared to
the previous population. Thus DE is an elitist
algorithm (Pant et al., 2009). Note that all vectors
(chromosomes) above consist of D elements as
follows
,, ,0, ,1, ,, , 1.
, ,..., ,...,
ijG i G i G ikG iD G
xxxxx
−
⎡⎤
=
⎣⎦
(6)
where i refers to the vector number in
population, j to the element index, and G to the
generation.
The overall algorithm can be summarized in the
following steps:
1. Create the initial population and evaluate its
fitness.
2. Apply mutation, crossover and selection. Each
chromosome acts as a target vector X
i,G
at a time.
For each target vector,
2.1 Select the base vector for mutation and the
vectors needed to calculate the difference vectors,
2.2 Calculate the mutant vector, V
i,G
,
2.3 Create the trial vector U
i,G
through crossover
and
2.4 Select X
i,G
or U
i,G
to be moved to the new
population.
3. Evaluate the fitness of the population
4. If the termination criterion is satisfied,
terminate, otherwise, go back to step 2.
Different variants of DE have been developed.
They differ in methods used for crossover, selection
and mutation. Also the number of difference vectors
may vary. Typically, different variations are denoted
as (Feoktistov and Janaqi, 2004)
c/b/a/DE
(7)
where a is the method for selecting the base
vector for mutation, b is the number of difference
vectors and c is the method used for crossover. The
number of difference vectors is typically 1 or 2.
Examples of different choices are shown in Table 3.
Table 3: Different DE algorithms tested in this study.
Base vector
selection for
mutation
Number of
difference
vectors
Crossover
method
DE/rand/1/bin Randomly 1 Binary
DE/rand/2/bin Randomly 2 Binary
DE/best/1/bin The best one 1 Binary
DE/rand-to-
best/1/bin
Compromise 1 Binary
DE/rand/1/exp Randomly 1 Exponential
Five different DE algorithms are studied here in
order to gain knowledge how different versions
apply to the identification problem. The studied
versions are
DE/rand/1/bin, DE/rand/2/bin,
DE/best/1/bin, DE/rand-to-best/1/bin and
DE/rand/1/exp. Two first ones are used to determine
if it is favourable to use more than one difference
vectors. The effects of different base vectors for
mutation are studied with
DE/rand/1/bin,
DE/best/1/bin and DE/rand-to-best/1/bin. Finally,
binomial and exponential crossover operators are
compared with
DE/rand/1/bin and DE/rand/1/exp.
3.2 Defining the Population Size
There are some parameters regulating the evolution
of the population in evolutionary algorithms. The
population size is one of them and it is essential
because it should be big enough so that the initial
population has enough diversity (i.e. the initial
population covers the whole search space) and as
small as possible to decrease the computational load.
In this study, entropy is used as the measure of
diversity. The same has been earlier reported in
(Sorsa and Leiviskä, 2010). The higher the entropy
the more diverse the population is. The entropy of a
random variable is given by (Cover and Thomas
2005)
(
)
(
)()
∑
−
=
xplogxpXH
(8)
where p(x) is the probability mass function of the
random variable X. The probability mass function
satisfies (Cover and Thomas, 2005)
(
)
∑
=
1xp
(9)
The base of the logarithm in (8) is 10 in this
study. For the case that p(x) contains zero
probability components, it is defined that (Cover and
Thomas, 2005)
000
=
log
(10)
DifferentialEvolutioninParameterIdentification-FuelCellasanExample
43
The entropy is at its maximum when the random
variable is uniformly distributed (Cover and
Thomas, 2005). Typically, and also in this study, the
initial population is taken from the uniform
distribution. When the initial population is too small
it does not follow the uniform distribution leading to
lower entropy. However, with increasing population
size the initial population is more uniformly
distributed and the entropy is closer to the
maximum. In this study, the entropy is calculated for
each parameter independently and those entropies
are then summed. The probability mass functions
use 10 bins in this study.
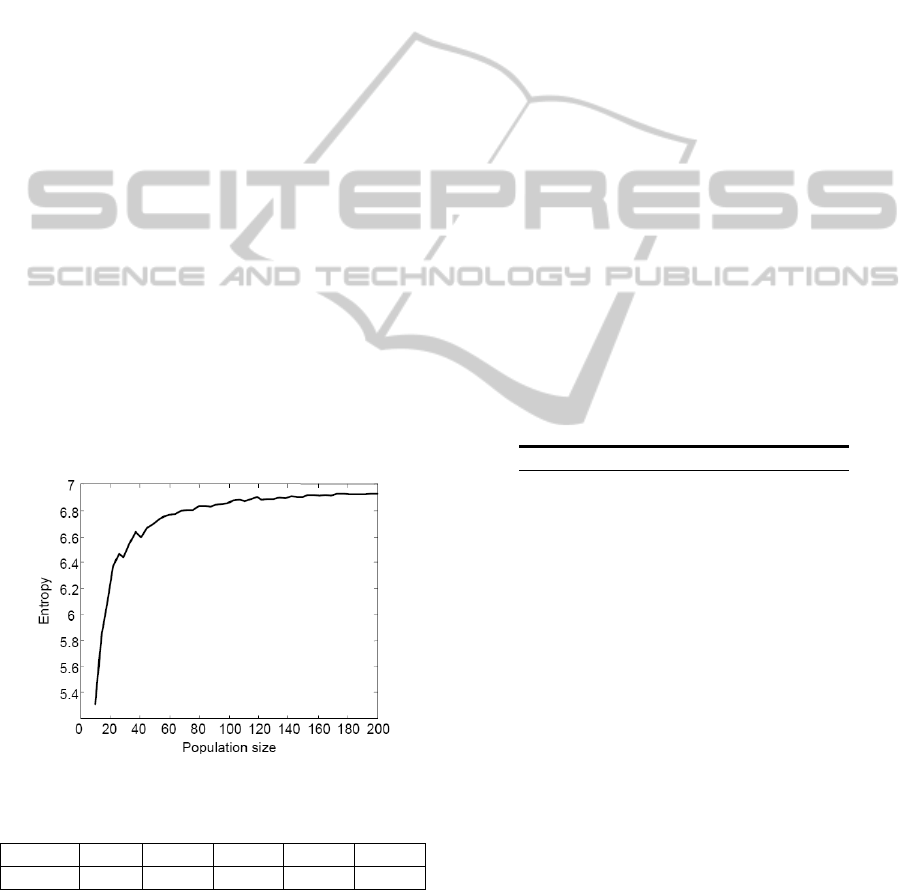
Figure 2 shows the entropy as the function of the
population size. For each population size, 10
different initial populations are created and their
entropies are calculated. The average of those is then
plotted in Figure 3. With 7 parameters and using the
10-based logarithm, the maximum entropy is 7.
Table 4 shows entropies with selected population
sizes. From Figure 3 and Table 4, it is clearly seen
that the initial steep rise of the entropy reaches a
plateau somewhere around the population size of
160 where about 99 % of the maximum entropy is
reached. With the population size of 100, almost 98
% of the maximum entropy is reached while almost
96 % is reached with the population size of 50. In
this study, it is assumed that reaching 95 % of the
maximum entropy is enough and thus the population
size of 50 is used with all algorithms.
Figure 2: Entropy as the function of the population size.
Table 4: Entropies at some population sizes.
Pop. Size 10 20 50 100 200
Entropy 5.31 6.24 6.70 6.85 6.93
3.3 Tuning Parameters
There are only a few tuning parameters in DE and
thus they should be defined carefully. DE is
sensitive especially to the mutation coefficient F and
the crossing coefficient CR (Tvrdik, 2009). The
appropriate values of the parameters depend on the
problem. The influence of all three parameters (F,
CR and NP) is similar. Small values increase the rate
of convergence but may lead to premature
convergence to a local optimum. (Fan and
Lampinen, 2003),
Some suggestions for the tuning parameters can
be found in the literature. As suggested in (Price et
al., 2005), a good initial guess for separable
functions are CR = 0.2 and F = 0.5. However, if the
parameters to be solved depend on each other, it is
stated in (Price et al., 2005) that efficient
optimization is obtained with CR = 0.9 and F ≥ 0.8.
To guarantee that the search is efficient and
mutation produces big enough step sizes, the
variance of the population compared to the state of
the search should be high enough. Because selection
favours the solutions near the optimum, it decreases
the variance of the population. Therefore it is desired
that mutation and crossover slightly increase the
variance. On the other hand, too high variance may
decrease the rate of convergence significantly.
Table 5 shows the studied DE algorithms together
with their tuning parameters.
Table 5: The tuning parameters of the studied DE
algorithms.
CR F
DE/rand/1/bin 0.35 0.9
DE/rand/2/bin 0.35 0.9
DE/best/1/bin 0.39 0.7
DE/rand-to-best/1/bin 0.56 0.9
DE/rand/1/exp 0.35 0.9
3.4 Selecting Base Vector for Mutation
When applying mutation two things have to be
considered: the direction and size of the change. In
differential evolution, these depend on the difference
vector and especially the vectors used to create the
difference vector. Thus increasing the population
size or the number of vectors used for building the
difference vector leads to more alternative mutation
directions. (Feoktistov and Janaqi, 2004)
Almost exclusively one or two difference vectors
are used. When one difference vector is used, the
mutant vector is obtained with (3) and with two
difference vectors, the mutant vector is (Storn and
Price, 1996)
,1, 2,3,
4, 5,
(
)
iG r G r G r G
rG rG
VX FX X
XX
=
+−
+−
(11)
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
44

3.4.1 Rand
The base vector for mutation can be selected
randomly. Then each chromosome has equal
probability to be chosen. The problem with purely
random selection is that same chromosomes can be
selected multiple times. Thus a better random
approach is to use universal stochastic sampling
where multiple chromosomes are selected at a same
time. A method where each chromosome is selected
only once is called permutation selection. An even
simpler approach is to select a random starting point
for the selection.
When random mutation is applied, the mutant
vector is given by (3). (Price et al. 2005)
3.4.2 Best
The best chromosome (X
best,G
) can be also used as
the base vector for mutation. It increases the rate of
convergence but may, however, lead to premature
convergence (Price, 1996). In such a case, the found
solution may be poor. Using the best chromosome as
a base vector is useful when the global optimum is
easy to find (Storn and Price, 1995).
The mutant vector when the best chromosome is
used as the base vector is
,, 2,3,
()
iG bestG r G r G
VX FX X=+ −
(12)
3.4.3 Rand-to-Best
Rand-to-best mutation is a combination of the
previous two methods for selecting the base vector
for mutation. The base vector is neither a random
nor the best chromosome of the population but a
combination of these. The base vector in rand-to-
best mutation is given by (Storn and Price, 1996).
()
,1, 2,3,
,1.
()
iG r G r G r G
wbestG rG
VX FX X
XX
λ
=+ −
−
(13)
Above, λ
w
is a weighting coefficient ranging
from 0 to 1 determining how close the base vector is
to the best chromosome. With high values of λ
w
the
mutant vector is close to the best chromosome and
with small values the mutant vector is close to the
random chromosome. To simplify the method, λ
w
may be defined to equal F.
3.5 Crossover
After mutation, crossover is applied in differential
evolution. In crossover, a trial vector is generated by
combining the mutant and the target vectors. The used
crossover method and the crossing coefficient CR
both have influence on how close to the mutant vector
the trial vector is. The closer the trial vector is to the
mutant vector the bigger step size is applied and the
algorithm proceeds faster. Typical crossover methods
are binomial and exponential crossover but also
arithmetic crossing is sometimes used (Zaharie,
2009).
3.5.1 Binomial Crossover
In binomial crossover, the elements are selected to
the trial vector from the mutant vector with the
probability CR and otherwise they are taken from
the target vector. The selection is made
independently for each element. Because it is
desired that the trial vector is not a duplicate of the
target vector, one element is forced to be taken from
the mutant vector. The trial vector according to the
binomial crossing is (Storn and Price, 1997)
,,
,,
,,
,() ()
,() ()
ijG
ijG
ijG
v if randb j CR or j rnbr i
u
x
if randb j CR or j rnbr i
≤=
⎧
⎪
=
⎨
≤≠
⎪
⎩
(14)
Above,
randb(j) is a uniformly distributed
random number between 0 and 1,
rnbr(i) is a
random integer between 1 and D, where D is the
number of optimized parameters and thus the length
of one chromosome. Because one of the elements is
forced to betaken from the mutant vector, the
probability that a parameter is taken from the mutant
vector does not equal
CR (pm≠CR). The probability
pm depends on the population size. When crossing,
the probability
pm for D-1 elements is CR and for
the rnbr(i):th element it is 1. Thus for one parameter
the probability is (Zaharie, 2009)
(
)
11
11
1
m
CR D
pCR
DD D
−+
⎛⎞
=−+=
⎜⎟
⎝⎠
(15)
The expected number of parameters taken from the
mutant vector is given by (Zaharie, 2009)
(
)
() 1 1
m
EL NPp NP CR
=
=− +
(16)
3.5.2 Exponential Crossover
Exponential crossover is similar to the one-point-
and two-point crossover operators in genetic
algorithms. L elements starting from a random point
are taken from the mutant vector and the rest of the
trial vector is taken from the target vector.
Exponential crossover is presented by (Storn and
Price, 1995)
DifferentialEvolutioninParameterIdentification-FuelCellasanExample
45

,,
,,
,,
, , 1 ... 1
,
ijG
D
DD
ijG
ijG
vifjnn nL
u
xotherwise
=++−⎧
⎪
=
⎨
⎪
⎩
(17)
Above, n is a random integer between 1 and D and
〈
n
〉
D
is the remainder of the division n/D. The
elements are taken from the mutant vector as long as
a generated random number is lower than CR. The
probability of taking an element from the mutant
vector and also the expectation for the overall
number of elements taken from the mutant vector
can be calculated. They are given, respectively, by
(Zaharie, 2009).
()
1
1
D
m
CR
p
D
CR
−
=
−
(18)
1
()
1
NP
CR
EL
CR
−
=
−
(19)
Compared to binomial, exponential crossover
requires a lot higher CR to obtain the same
expectation E(L). Practically, only in cases where
CR is close to 1, the majority of the elements in trial
vector are taken from the mutant vector. Thus if the
problem is such that mutation is critical in finding
the optimum, binomial crossing is to be used. With
exponential crossing, defining an appropriate CR is
also harder because the correlation between CR and
pm is nonlinear while in binomial crossing it is
linear. Thus the majority of the applications
nowadays uses binomial crossing (Zaharie, 2009).
4 RESULTS AND DISCUSSION
The optimizations are repeated 500 times for each
studied version of the algorithms and statistical
information about the performance of the algorithms
is obtained from the repetitions. The best model
during each optimisation is recognised and their
accuracy is evaluated through the SSEP objective
function given in (2). The mean value, standard
deviation and minimum of the best objective
function are calculated for each optimisation.
Each repetition of the algorithm gives the
possible best solution to the parameter identification
problem. Thus a distribution of the parameters with
500 observations is obtained through the repetitions.
To convert the distributions into an informative
index, entropy is used. Smaller entropy means less
variance throughout the repetitions. Thus the smaller
the entropy the better the algorithm has converged.
4.1 The Performance of DE Algorithms
The minimum and mean values and standard
deviations of SSEP for DE algorithms are given in
Table 6. It shows that no big differences exist at
least when considering the minimum and average
results. Table 7 gives the best parameter sets for
different DE versions. This table shows more
differences meaning that this problem has several
local minima. Only ξ
3
and B remain almost the same
despite the algorithm. Also λ obtains similar values
with the exception that DE/rand/2/bin gives a higher
value than the other algorithms. The entropies of the
parameters are given in Table 8. The table shows
that ξ
3
and B have low entropy which means that the
same values are obtained throughout the repetitions.
High entropies are noticed especially with ξ
1
, ξ
2,
ξ
4
and R
C
. The performance of the best models is
presented in Tables 9 and 10. No significant
differences can be noticed in the model performance
for the training data sets (Table 9). However, the
performance for the testing data sets (Table 10)
shows that the best results are obtained when using
the rand-to-best -strategy in base vector creation. In
Table 11, information already given in earlier tables
is collected and refined. It shows the SSEP values
for the training and testing data sets and the overall
entropy. In the following subsections, the results
provided in Tables 6-11 are analyzed in more details
in order to draw conclusions about the significance
of the different operators used in DE.
4.2 Influence of the Number of
Difference Vectors
The effect of the number of difference vectors can
be analysed when comparing the performance of
DE/rand/1/bin and DE/rand/2/bin algorithms. As
mentioned before, the statistical values from the 500
repetitions of both of the algorithms show no
significant differences (Table 6). Also the
performance of the best models for the training data
sets is almost the same as shown in Table 9.
However, the best parameter vectors differ as shown
in Table 7. The entropies of the parameters in 500
repetitions of the algorithms (Table 8) indicate that
DE/rand/2/bin has achieved a bit higher rate of
convergence. For both algorithms, only parameters
ξ
3
and B have low entropies which explains this
behaviour. The performance of the best models for
the testing data sets (Tables 10 and 11) shows that
DE/rand/2/bin gives better results because the SSEP
values are lower compared to the DE/rand/1/bin.
The exception is data set 1 for which DE/rand/1/bin
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
46

Table 6: Statistical values of the SSEPs in 500 repetitions of the DEs.
Algorithm Minimum Mean Standard deviation
DE/rand/1/bin 5.070 5.152 0.075
DE/rand/2/bin 5.076 5.165 0.044
DE/best/1/bin 5.066 5.117 0.070
DE/rand-to-best/1/bin 5.066 5.080 0.033
DE/rand/1/exp 5.069 5.146 0.064
Table 7: The best parameter values found by the DE algorithms.
ξ
1
ξ
2
[
⋅
10
-3
] ξ
3
[
⋅
10
-4
] ξ
4
[
⋅
10
-5
] B λ R
c
[
⋅
10
-3
]
DE/rand/1/bin -0.117 1.108 -1.148 10.936 0.033 11.858 0.002
DE/rand/2/bin -0.419 1.781 -1.159 9.621 0.034 12.113 0.020
DE/best/1/bin -0.765 2.542 -1.157 8.076 0.033 11.887 0.000
DE/rand-to-best/1/bin -0.700 2.400 -1.158 8.367 0.033 11.891 0.000
DE/rand/1/exp -0.191 1.277 -1.146 10.631 0.033 11.858 0.002
Table 8: The entropies of the parameters in 500 repetitions.
H(ξ
1
) H(ξ
2
) H(ξ
3
) H(ξ
4
) H(B) H(
λ
) H(R
c
)
DE/rand/1/bin 0.93 0.63 0.16 0.84 0 0.51 0.78
DE/rand/2/bin 0.92 0.61 0.20 0.82 0 0.42 0.79
DE/best/1/bin 0.95 0.68 0.06 0.89 0 0.46 0.66
DE/rand-to-best/1/bin 0.95 0.68 0.01 0.86 0 0.27 0.29
DE/rand/1/exp 0.92 0.61 0.16 0.81 0 0.51 0.75
Table 9: The performance of the best models for the training data sets (Data set 1 / Data set 2).
Error mean Error st.dev. SSEP
DE/rand/1/bin 0.00 / -0.01 0.39 / 0.46 2.10 / 2.97
DE/rand/2/bin -0.01 / -0.02 0.40 / 0.45 2.19 / 2.89
DE/best/1/bin 0.00 / 0.00 0.39 / 0.45 2.17 / 2.90
DE/rand-to-best/1/bin 0.00 / 0.00 0.39 / 0.46 2.16 / 2.91
DE/rand/1/exp 0.00 / -0.01 0.40 / 0.45 2.24 / 2.83
Table 10: The performance of the best models for the testing data sets (Data set 3 / Data set 4).
Error mean Error st.dev. SSEP
DE/rand/1/bin -0.22 / -0.11 0.25 / 0.31 1.66 / 1.51
DE/rand/2/bin -0.08 / -0.06 0.26 / 0.30 1.04 / 1.31
DE/best/1/bin 0.10 / 0.02 0.26 / 0.30 1.10 / 1.27
DE/rand-to-best/1/bin 0.07/ 0.01 0.26 / 0.30 1.00 / 1.27
DE/rand/1/exp -0.19 / -0.10 0.27 / 0.30 1.52 / 1.39
Table 11: The performance of the DE algorithms. Note that the SSEP values here are sums of values given for two data sets
in Tables 9 and 10.
rand/1/bin rand/2/bin best/1/bin rand-to-best/1/bin rand/1/exp GA
SSEP train 5.07 5.08 5.07 5.07 5.07 5.07
SSEP test 3.18 2.35 2.37 2.27 2.91 2.48
Entropy 3.85 3.76 3.69 3.06 3.76 4.92
gives a lower SSEP value. From the results, it can be
concluded that higher rate of convergence is
achieved when using 2 difference vectors instead of
1. This higher rate of convergence leads to better
solutions when the number of generations is limited
to some predefined value. Thus the use of 2
difference vectors is beneficial in this case.
DifferentialEvolutioninParameterIdentification-FuelCellasanExample
47

4.3 Influence of the Base Vector for
Mutation
The influence of the base vector for mutation is
evaluated by comparing DE/rand/1/bin,
DE/best/1/bin and DE/rand-to-best/1/bin
algorithms. Table 6 already indicates that DE/rand-
to-best/1/bin performs best on average even though
the best models show almost the same prediction
accuracy for the testing data sets (Table 10). When
studying the entropies of the solutions (Tables 8), it
is noticed that the lowest entropy is obtained with
DE/rand-to-best/1/bin indicating that the highest
rate of convergence is achieved with this algorithm.
This leads to clearly better prediction accuracy for
the testing data sets as shown in Tables 10 and 11.
The results provided show that it is advantageous
to use rand-to-best -strategy for selecting the base
vector for mutation.
4.4 Influence of the Crossover
Operator
The influence of the crossover operator can be
evaluated by studying DE/rand/1/bin and
DE/rand/1/exp algorithms. The results obtained with
the algorithms are almost equal. A slight difference
can be noticed from Table 8 and 11, which shows that
DE/rand/1/exp achieves a bit lower entropy and also a
bit lower SSEP for the testing data sets. However, the
difference is quite small and thus no suggestion about
the preferred algorithm can be given.
4.5 Comparison of the DE Algorithms
The DE algorithms are compared based on the
results given in Table 11. From the table, it is seen
that all the algorithms are able to reach almost equal
value for the training data SSEP. When the SSEP of
the testing data sets is investigated, it is seen that
DE/rand-to-best/1/bin gives the best results. Also
the overall entropy shows that the solutions found by
DE/rand-to-best/1/bin are close to each other
throughout the 500 repetitions. Thus DE/rand-to-
best/1/bin is the most suitable algorithm for the
studied problem. DE/best/1/bin and DE/rand/2/bin
show almost equal results and perform quite well
also. DE/rand/1/bin and DE/rand/1/exp exhibit the
poorest prediction accuracy and performance.
5 CONCLUSIONS
In this study, evolutionary algorithms were studied
and used for identifying the parameters of a fuel cell
model. The fuel cell model was nonlinear having 7
parameters. Five different DE algorithms were tested
and compared. DE varied in the number of
difference vectors, the selection of the base vector
for mutation and the crossover operator. The studied
DE algorithms were DE/rand/1/bin, DE/rand/2/bin,
DE/best/1/bin, DE/rand-to-best/1/bin and
DE/rand/1/exp. An appropriate population size for
all the algorithms was defined based on the plot of
the entropy of the initial population as the function
of the population size.
DE/rand-to-best/1/bin showed to be the most
suitable algorithm for the studied problem. Selection
of the crossover operator has no considerable effect
on the results.
REFERENCES
Bergey P. K. Ragsdale C. Modified differential evolution:
a greedy random strategy for genetic recombination.
Omega 2005; 33: 255-65.
Chakraborty, U. K., Abbott, T. E., Das, S. K. PEM fuel
cell modeling using differential evolution. Energy
2012; 40: 1, 387 – 399.
Chipperdale A. Introduction to genetic algorithms. In:
Zalzala AMS, Fleming PJ, editors. Genetic algorithms
in engineering systems, Stevenage, Herts: The
Institution of Electrical Engineers; 1997, p. 1-45.
Cover TM, Thomas JA. Elements of Information Theory.
Hoboken, N.J.: Wiley; 2005.
Fan H. Y, Lampinen J. A Trigonometric Mutation
Operation to Differential Evolution. J Global Optimiz.
2003; 27: 105-29.
Feoktistov V., Janaqi S. Generalization of the strategies in
differential evolution. In: Proceedings of the 18th
International Parallel and Distributed Processing
Symposium (IPDPS’04), Santa Fe, New Mexico: IEEE
Press; 2004, 165a, 2004.
Ikonen E, Najim K. Advanced process identification and
control. New York: Marcel Dekker; 2002.
Katare S., Bhan A., Caruthers J. M., Delgass W. N.,
Venkatasubramanian V. A hybrid genetic algorithm
for efficient parameter estimation of large kinetic
models. Comput. Chem. Eng. 2004; 28: 2569-81.
Larminie J., Dicks A. Fuel cell systems explained, 2nd
edition. West Sussex, England: John Wiley & Sons
Ltd; 2003.
Mann R. F., Amphlett J. C., Hooper MAI, Jensen H, M,,
Peppley BA, Roberge PR. Development and
application of a generalised steady-state
electrochemical model for a PEM fuel cell. J Power
Sources 2000; 86: 173-80.
Mo Z. J., Zhu X. J., Wei L. Y., Cao G. Y.. Parameter
optimization for a PEMFC model with a hybrid
genetic algorithm. Int. Journal Energy Res. 2006; 30:
585-97.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
48

Ohenoja M., Leiviskä K.: Validation of genetic algorithm
results in a fuel cell model. Int. J Hydrogen Energy
2010; 35: 618-25.
Pant M., Ali M., Abraham A.. Mixed Mutation Strategy
Embedded Differential Evolution. In: 2009 IEEE
Congress on Evolutionary Computation, Trondheim,
Norway: IEEE Press; 2009, p. 1240-6.
Price K. V. Differential evolution: a fast and simple
numerical optimizer. In: Smith M.H. et al. (eds.):
Proceedings of the 1996 Biennial Conference of the North
American Fuzzy Information Processing Society –
NAFIPS, Berkeley. 524-527.
Price K. V., Storn R. M., Lampinen J A. Differential
evolution: a practical approach to global
optimization. Berlin, Springer: 2005.
Sarker R, Kamruzzaman J, Newton C. Evolutionary
Optimization (EvOpt): A Brief Review and Analysis.
Int. J Comp. Intell. Appl. 2003; 3: 311-30.
Sorsa A. Koskenniemi A. Leiviskä K. Evolutionary
algorithms in nonlinear model identification. Control
Engineering Laboratory, University of Oulu. Report
A44, 2010.
Sorsa A, Leiviskä K. Parameter identification of a fuel cell
model with genetic algorithms In: Proceedings of the
51st Conference on Simulation and Modelling, SIMS
2011, October 14-15, Oulu, Finland; 2010, 6p.
Storn R, Price K. Differential Evolution - A Simple and
Efficient Heuristic for Global Optimization over
Continuous Spaces. J Global Optimiz. 1997; 11: 341-
59.
Storn R, Price K. Differential Evolution - A simple and
efficient adaptive scheme for global optimization over
continuous spaces. International Computer Science
Institute, University of California: Technical Report
TR-95-012; 1995.
Storn R. and Price K. (1996) Minimizing the real
functions of the ICEC’96 contest by differential
evolution. In: Proceedings of the 1996 IEEE
international conference on evolutionary computation,
Nagoya. 842-844.
Storn R. and Price K. (1997) Differential Evolution - A
Simple and Efficient Heuristic for Global
Optimization over Continuous Spaces. Journal of
Global Optimization 11, 341-359.
Tvrdík J. Adaptation in differential evolution: A numerical
comparison. Applied Soft Comput. 2009; 9: 1149-55.
Wolf D, Moros R. Estimating rate constants of
heterogeneous catalytic reactions without supposition
of rate determining surface steps – and application of a
genetic algorithm. Chem. Eng. Sci. 1997; 52: 2589-99.
Zaharie D. (2009) Influence of crossover on the behavior
of Differential Evolution Algorithms. Applied Soft
Computing 9, 1126-1138.
Zaharie D. Critical Values for the Control Parameters of
Differential Evolution Algorithms. In: Matousek R,
Osmera P, editors. Proceedings of Mendel 2002, 8th
International Conference on Soft Computing, Brno;
2002, p. 62-7.
DifferentialEvolutioninParameterIdentification-FuelCellasanExample
49
